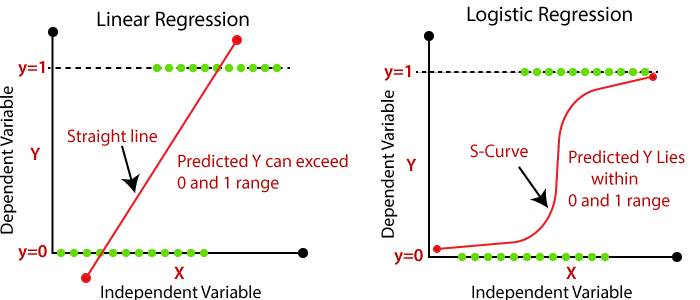
ML 문제의 2가지 큰 유형
- 회귀 문제(Regression)
- 분류 문제(Classification)
The main difference between Regression and Classification algorithms is that Regression algorithms are used to predict the continuous values such as price, salary, age, etc. While, Classification algorithms are used to predict/classify the discrete values such as Male or Female, True or False, Spam or Not Spam, etc.
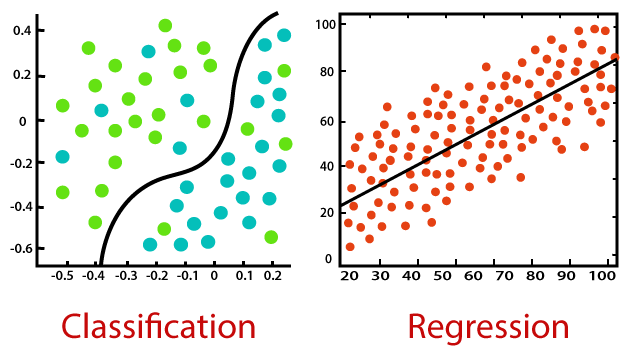
그리고 대표적으로 회귀 문제에는 선형회귀분석(Linear Regression), 분류 문제에는 로지스틱 회귀(Logistics Regression) 방법론이 사용된다. 이때, 로지스틱 회귀의 경우 이름만 회귀이고 실질적으로는 분류 문제에 사용되는 방법이라는 것을 숙지하자! (교수님 말씀을 빌리자면 붕어빵 안에 붕어가 안들어가있듯이 ㅋㅋ)
Linear Regression vs Logistic Regression
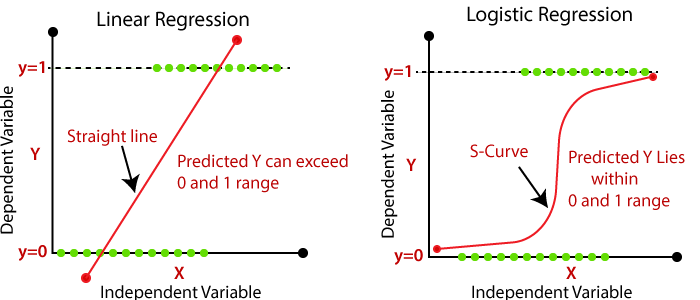
우선 본 문서의 결론은 위 그림으로 귀결될 수 있는데, 차근차근 그 과정에 대해서 알아보고 다시 한 번 그림을 살펴보도록 하자.
1. Linear Regression
Linear Statiscal Model이란?
Linear Statiscal Model이란 독립 변수 ()와 종속 변수 간의 관계를 선형의 모델로 정의하는 모델이다.
- : 우리가 독립변수 를 통해서 추정하려고 하는 종속변수
- : 우리에게 주어진 데이터들로, Y를 추정하기 위한 재료이다.
- 회귀계수 : 독립변수 에 곱해져있는 는 회귀계수라고 불리며 우리가 선형회귀 모델을 통해서 추정하려고 하는 핵심적인 값, 즉 모수(parameter)이다.
- : 회귀식의 오차항으로, 기댓값이 0인 확률 변수 (는 이미 알고있는 값이기 때문에 추정치를 의미하는 을 사용하지 않음에 주의!)
이 때, 독립변수 가 1개면 단순선형회귀분석(simple linear regression), 여러개면 다중선형회귀분석(multiple linear regression)이라고 한다.
SSE (단순선형회귀분석 가정)
- 우리는 모수의 추정량인 을 찾는게 목적 !
LSE(Least-Square Method)
- n개의 데이터 포인트에 대해서 회귀식(Fitted Line)을 학습시키는 방법
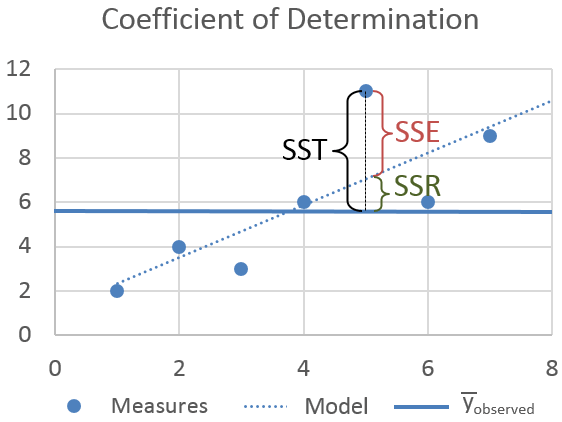
- Fitted Line과 실제값 간의 차이(vertical deviation = error)의 제곱합(SSE)을 최소화시키는 것이 목적. 즉, Minimize SSE가 목표.
- Fitted Line
- Sum of Squares of the vertical deviation(Sum of Squares of Error) =
를 최소로 만들기 위해서는 에 의해 영향을 받을 것이므로 두 변수에 대해 를 편미분하고, 이 때 가 0이 되는 값을 찾아내는 기초적인 최적화 방법이다
2. Logistic Regression
일단, 로지스틱 회귀 모형에서는 선형 회귀 모델과는 다르게 독립변수 의 값이 0 또는 1 Binary하게 도출되는 것이 가장 큰 특징이다.
그리고 이러한 특징은 자연스럽게 True/False 여부를 판별하는 분류 문제로 이어질 수 있게 된다. (ex. 이 사람이 이 상품을 좋아할 것인가(True), 안 좋아할 것인가(False) 등)
Logistic Function
위 함수를 쉽게 표현하면, input으로는 부터 까지 전부 받고, output으로는 0과 사이의 값을 뱉는 함수이다.
- : 함수의 중간 지점 (midpoint)
- : 함수의 최댓값 (curve's maximum value)
- : 함수의 기울기(steepness of the curve)
모델을 좀 더 단순화하면 아래와 같을 수 있다.
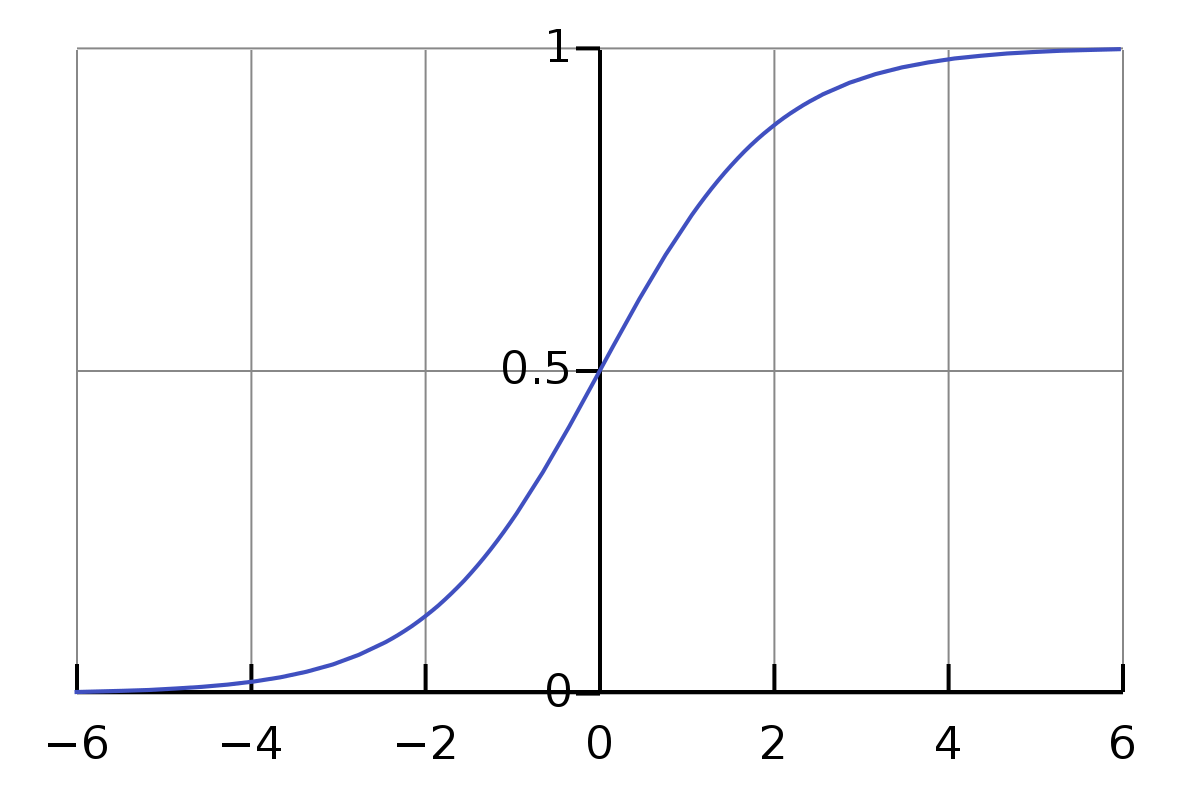
Standard Logistic Function
-
-
위 함수는 가 0이고, 이 1인 경우에 해당. 즉, 중간 지점이 0이고 최대치는 1인 경우.
Logistic Regression의 목적식
- 선형회귀분석과 마찬가지로, 학습을 위해서는 목적식이라는게 필요함. SSE를 최소로 만들었던 것처럼, 로지스틱 회귀에서는 손실값을 최소로 만드는 방법을 사용.
- 주로 Cross-Entropy Loss(CE)를 사용하여 모델을 학습시킨다.
먼저, 목적식을 사용하기 전에 을 구해야 함. 즉, 특정 데이터가 주어졌을 때 해당 데이터가 참일 확률을 구하여 손실함수에 반영해야 함.
- 손실 함수 :
위 수식으로 정의되는 손실 함수의 값을 낮게 만드는 것이 목적 ! 수식의 구조에 의하면...
- 가 1일때 가 낮아지려면, 도 높은 값을 가져야 함
- 가 0일때 가 낮아지려면, 도 낮은 값을 가져야 함
우리가 학습해야할 값은 로지스틱 회귀 함수의 정의역에 곱해지는 의 값으로, 는 를 최소화하도록 최적화되어야 한다. (Gradient Descent 방식을 사용; )
