본 포스팅은 기업재무론(Corporate Finance)에서 배우는 CAPM(Capital Asset Pricing Model)을 좀 더 깊게 이해하고자 정리한 공부 포스팅입니다 :)
CAPM에 대하여
CAPM(Capital Asset Pricing Model)
CAPM은 간단히 말해서 "기업의 이해관계자(주주, 채권자, 정부), 재무적 성과(FS)를 동시에 고려하여 주식의 가치를 평가(Valuation)"하는 이론적 도구이다.
CAPM의 수학적 정의
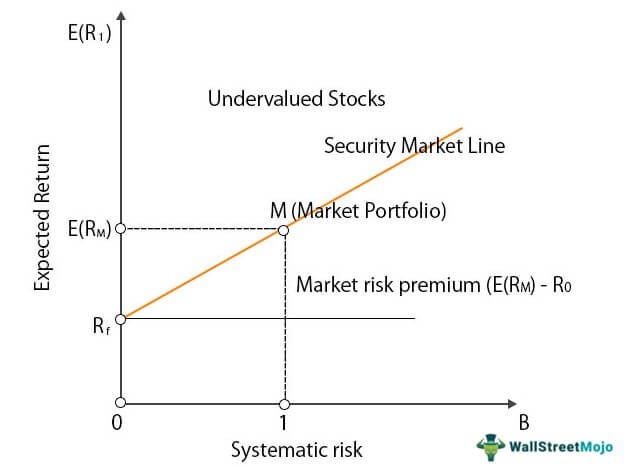
위 정의식을 "선형회귀모델(linear statiscal model)"의 관점에서 바라보면, 은 를 회귀계수로 갖고, 절편을 로 가지며 독립변수로는 를 취하는 선형회귀식으로도 볼 수 있다. 가 1인 것을 보통 기준점으로 두기 때문에 해당 내용을 반영하여 2차원 그래프로 표현하면 아래와 같다.
[Figure 1 : CAPM and SML]
의 의미에 대하여
위 CAPM을 이루고 있는 변수 중에 라는 친구가 있다. 필자는 이 친구를 표현하기를 시장 위험 계수라고 적어두었는데, 그 이유는 가 아래와 같이 정의되기 때문이다.
이때 은 번째 주식의 수익률과 시장 전체의 수익률 간의 상관성을 나타내는 Covariance(공분산)이고, 은 시장 전체의 수익률의 Variance(분산)을 나타낸다.
CAPM에 대한 엄밀한 해석
앞서 말했던 "주식의 가치를 평가하기 위한 모델"이라는 말은 CAPM을 이해하는 데에 있어서 매우 Naive한 정의이고 보다 엄밀히 말하면, CAPM 자체로는 Asset Price를 계산할 수 없다.
그럼 CAPM은 뭐에 쓰이나?
Asset Price는 모델의 사후적 종착역일 뿐이고, CAPM은 개별 기업에 대한 할인율(Discount Rate) 또는 수익률을 계산하는 모델이다. (뒤에서 보겠지만, CAPM의 정의는 , 즉 개별 기업에 대한 기대수익률을 계산하는 과정이다)
예를 들어.. 실무적으로 DCF를 활용할 때에는 아래와 같은 방식으로 CAPM을 사용하고 Asset Price(Equity Price)를 계산하는 데에 가져다 쓰는 비율로서 활용한다.
WACC(Weighted Average Cost of Capital) & Equity Cost (CAPM)
[Figure 2 : WACC Calculation]
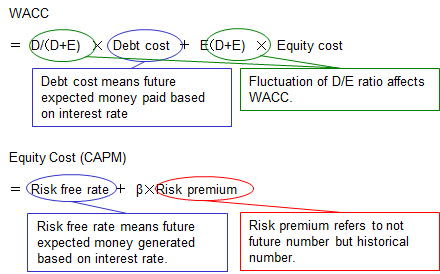
위 구조에서 Debt Cost(), Equity Cost()라는 것이 보이는데, 기업 입장에서 표현하면 의 경우 채권자에게 지급할 이자율, 의 경우 주주에게 지급할 수익률이며 이들을 (자본 비용)이라고 부른다.
그리고 CAPM이 뱉어내는 이 바로 Equity Cost()이다. (채권자에게 지급할 이자율인 와는 관계가 없다)
CAPM의 종착역 : Enterprise Value
[Figure 3: Enterprise Value Calucation towards Equity Value]
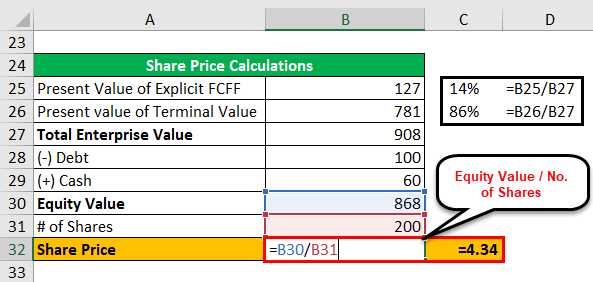
위 테이블의 A27 셀을 보면, 라는 데이터가 있다. DCF를 기준으로, CAPM은 이 라는 것을 최종적으로 계산하는데까지 활용되는 하나의 재료가 된다.
위 Valuation의 중요한 근간은 Gordon의 영구성장모형이다.
중요한 것은, 는 모든 이해관계자의 부를 전부 다 고려하는 변수이기 때문에 할인율로서 을 필수적으로 요구한다는 점이다. Equity Value는 그 다음이다. 전체 구조는 아래와 같이 쉽게 볼 수도 있다.
[Figure 4 : Enterprise Value Calculation]
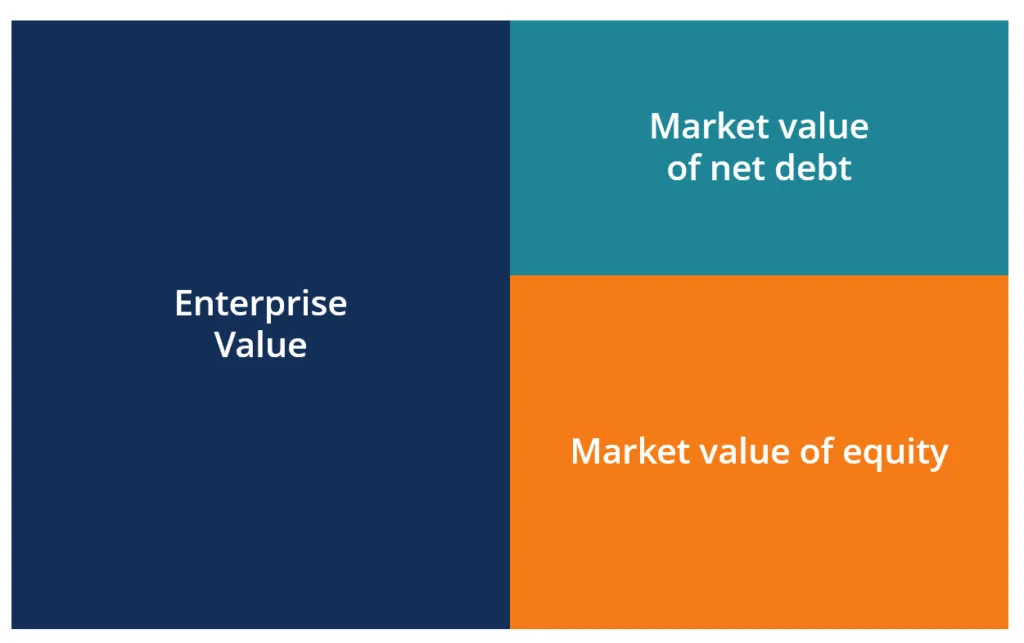
에서 Net Debt(순부채)를 제외하고 나면 순전히 주주의 부로 정의되는 Equity Value가 남게 된다. (참고적으로, 재무적 측면에서 기업의 부는 채권자 정부 주주로, 주주는 최후순위 청구권자에 해당한다)
CAPM은 factor를 넣으면 가격을 뱉는 마법이 아니다
Pricing Model이라는 명칭이 마치 특정 재화의 가격을 계산하는 모델인 것처럼 보인다. 그렇지만 CAPM이 Capital Asset의 가격을 계산해 주지는 않는다. 가령, 어떤 함수가 개의 원소로 이루어진 벡터 를 인자로 받을 때, 자산의 가격( )을 뱉는다면 아래와 같은 꼴로 모델의 뼈대가 만들어질 것이다.
그러나, CAPM은 위와 같은 구조로 차원 벡터를 하나의 가격으로 변환시켜주는 함수는 아니다. 아마도 Technical Analysis에서는(잘은 모르지만), 위와 같은 형태의 함수가 future price를 예측하는 데에 쓰일지도 모르겠다!
할인율로서의 CAPM
다시 돌아오면, CAPM은 자산의 가격을 계산할 때 필요한 할인율(Discount Rate)만을 제공해 줄 뿐이다.
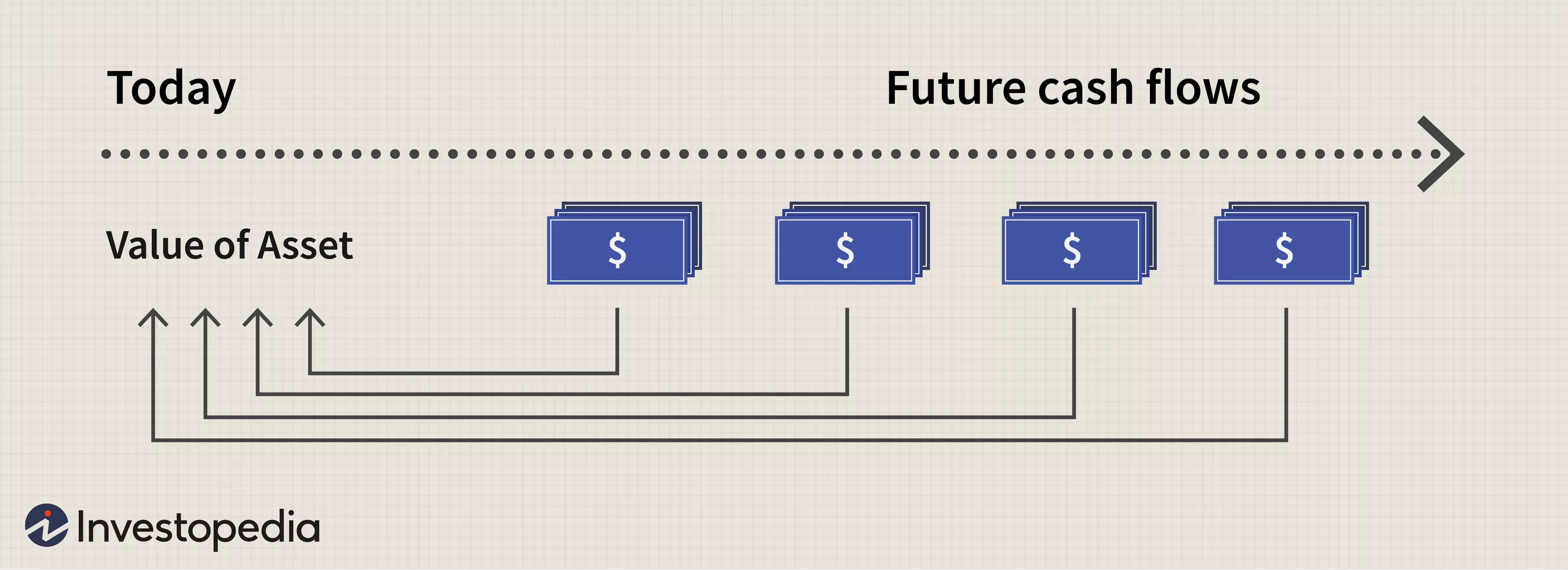
우리가 현재가치법(DCF Method)을 이용해 자산 가격을 계산할 때, 먼저 자산이 창출해 낼 미래의 현금흐름을 추정하고, 이렇게 추정된 미래의 현금흐름을 현재의 가치로 환산하는데, 이처럼 미래의 현금흐름을 현재가치로 환산할 때 사용하는 할인율을 CAPM이 제공해 주는 것이다.
[Figure 5 : FCFF Valuation Idea : Let's Discount !]
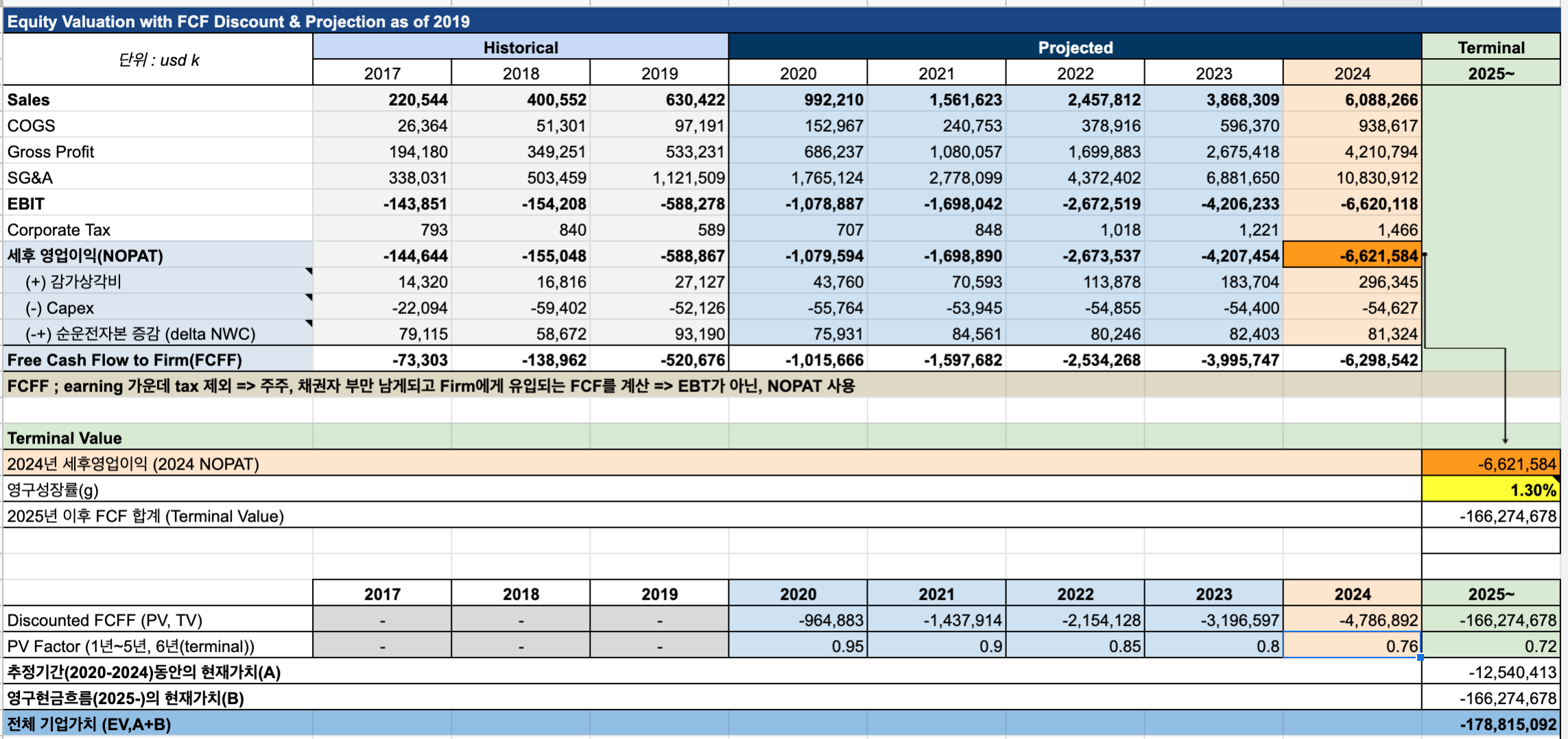
필자가 한창 Valuation, 주식 투자를 공부하면서 만든 DCF 모델은 아래와 같이 이루어져 있다. (실무에서는 보통 표준화된 financial modeling sheet를 사용하기도 한다)
Sample Model for DCF Method
[Figure 6 : Sample DCF Valuation Sheet]
CAPM의 가변성과 현금흐름 예측 (Quoted)
할인율은 자산(기업)의 상황에 따라 달라진다. 예를 들어, 삼성전자 주식 가치를 계산하기 위해 사용하는 할인율과 현대자동차 주식에 적용하는 할인율이 다르고, 또 같은 업종 내에서도 삼성전자와 LG전자에 적용하는 할인율이 다르다. 이는 각각의 기업이 갖고 있는 사업의 특성과 이에 따른 위험 정도가 서로 다르기 때문이다. CAPM은 이러한 위험 수준을 고려해서 적절한 할인율을 계산해 내는 모델인 것이다.
그런데 자산 가격을 산출하기 위해서는 할인율만 안다고 되는 것이 아니라, 미래의 현금흐름도 알아야 한다. 할인율을 책정하는 것도 어려운 일이지만, 미래의 현금흐름을 추정하는 것 또한 매우 어려운 일이다.
그러나 CAPM은 이 같은 미래의 현금흐름을 추정하는 데에는 전혀 쓸모가 없다. 그런 면에서는 CAPM의 Pricing Model이라는 표현이 좀 과장된 것이라 생각할 수도 있겠지만, 학문적으로 CAPM을 도출한 과정을 자세히 살펴 보면 이러한 표현이 타당한 것임을 알 수 있다.
그 밖의 Valuation 방법론
Comps Valuation Modeling
다수의 기업의 재무적 성과를 비교하여 도출되는 배수(Multiple)를 사용하여 특정 기업의 가치를 평가하는 Comparable Valuation 방식도 존재하며, 상대가치평가 방법으로 분류한다.
Residual Income Modeling
한편, 절대가치평가의 또 하나의 유형으로는 잔여이익모델(Residual Income Model)이 있다. DCF와 마찬가지로 타 기업을 고려하지 않고 회사 내의 재무 구조 내에서만 계산을 하지만, 정부와 채권자를 무시하고 자기자본비용(Cost of Equity)만 고려한 구조의 Valuation 방법이다.
M&A나 Equity Research 분야에서 실무를 경험해본 사람들이라면, 앞서 살펴본 DCF Equity Valuation 모델링 시트 뿐만 아니라, 위 2가지 밸류에이션 방법론 역시 매우 숙달된 상태일 것이다.
