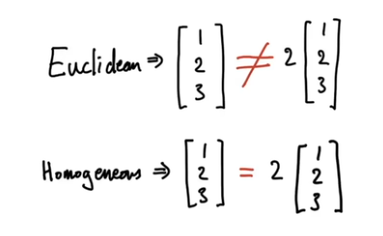[SLAM] 6. 동차좌표계

1. Projective geometry

• 사영 기하학
• 3D 세상은 유클리디안 geometry를 따른다
  • 두 직선이 평행 = 절대 만나지 않는다 = 유클리
  • 유클리디 기하학에서 두 직선이 평행 = 무한의 거리에서 두 선이 교차한다.
  • 무한을 숫자로 표현할 수 없다
  • 평행, 교차의 개념은 동시에 표현될 수 없다
• 사진 속에서 철도는 평행해보이지 않는다
  • 교차점 = 소실점 = 지평선이 있는 곳
• 원근법
  • 투영과정 즉, 3D에서 2D로 변환하는 과정에서 depth 정보가 소실
  • 유클리디안 transform은 orthogonality, 평행함 등을 유지해야하지만 project geometry는 orthogonality, scale, 평행함도 유지할 필요가 없다.
  • 다만, 직선인 물체가 직선으로 나와야한다는 것은 유지해야한다.

Vanishing point

• 3D 세상의 무한의 거리는 2D 이미지에서 유한하게 표현할 수 있다.
  -> 무한의 거리를 수학적으로 표현할 수 있다는 것
• projective geometry의 특징
  • 무한의 거리의 교차점을 표현할 수 있다
  • 무한, 유한을 모두 수로 표현할 수 있다

geometries

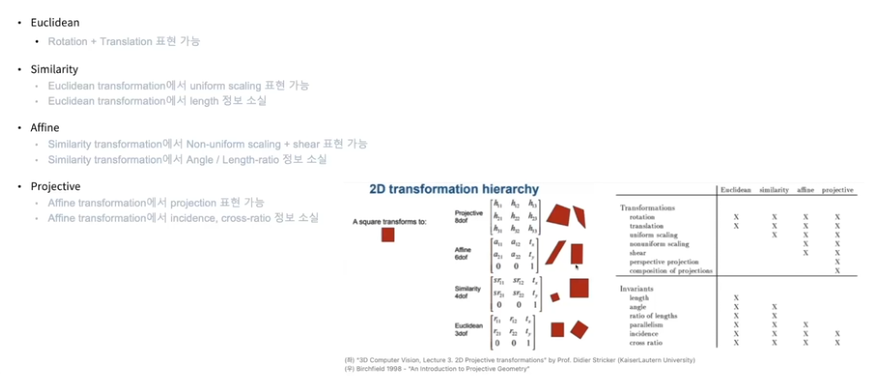
homogeneous coordinates

• 투영과정을 정확히 수식으로 표현할 수 있게 되었다
• project geometry : N+1 차원을 N 차원으로 투영, 차원 축소를 진행
• (x,y,z)(scale)
  • 실제 차원의 coordinates system에 scale 정보까지
  • 3차원이 2차원으로 투영될 때 지니고 있는 스케일 값에 대한 것

---

2. Homogeneous coordinates

plucker 정의

• x 객체(Homogeneous coordinates)에 0이 아닌 어떤 스칼라 값을 곱해도 그 coordinates는 같은 객체를 의미
  
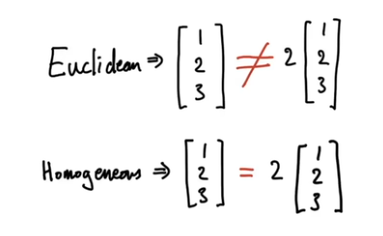
• 차원 중 하나는 scale에 대한 차원
  • 스칼라 값이 곱해진 값을 scale로 나누면 원래대로 된다
    

projective space - visualized

• 유클리디안 space
  • w축 : scale 의미, w=1인 경우가 2D 유클리디안 space
    
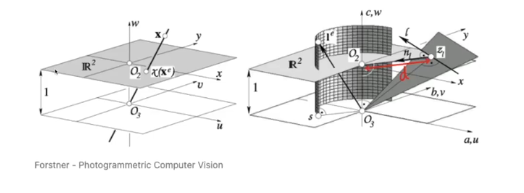
  • 유클리디안 space의 point 하나는 projective space에서 직선
  • 유클리이안 space 에서 직선은 projective space에서 평면

euclidean space vs projective space

• euclidean space
  • cartisian coordinates
  • projective space의 일부 (w=1인 공간)
• projective space
  • homogeneous coordinates
• cartisian -> homogeneous : scale값을 함께 표현해주면 된다.
• homogeneous -> cartisian : scale값으로 모든 값을 나누어 scale을 1로 낮추고 1을 제거하면된다

homogeneous SO(3)