1. 3D Rigid Body Motion
Rigid Body
- 강체
- 3D 공간 속에 물체의 위치를 x,y,z로 표현할 수 있다.
- 위치와 방향성도 가지고 있다.
- pose = Position + Orientation
- position = (tx, ty, tz)
- orientation = (Rx, Ry, Rz)
- 6 DoF = 3D orientaion + 3D pose = (tx,ty,tz,Rx,Ry,Rz)
Coordinate transformation
- 카메라 coordinate system에서의 (tx,ty,tz,Rx,Ry,Rz)는 실제 coordinataion system에서 어떻게 표현될까?
- 두개의 coordinate system 간의 orientation과 pose 변화를 알면된다!
- orientation의 차이는 rotation으로 표현할 수 있다.
- pose의 차이는 translation으로 표현할 수 있다.
- Rigid body motion
- 3D -> 3D 변환을 의미
- 유클리디언 transformation이라고도 한다
- 유클리디언 공간에서 좌표 표기법은 cartesian coordinate라고 한다
2. 다양한 회전 표현법
Euler Angle
- roll / pitch / yaw
- 각각의 축을 의미
- 3D rotation을 표현하기 위해 차례로 변환을 해줘야 한다
- 회전각의 순서, (rx,ry,rz)뿐만아니라 회전의 순서로 항상 함께 알려줘야한다
- 장점
- 이해하기 쉽다
- 단점 -> SLAM에서는 오일러 각도를 사용하지 않는다
- 최적화하기 어렵다 : 최적화를 위해서는 미분이 가능해야하는데 오일러 angle은 미분이 불가능하다
- gimbal lock : 회전 자유도가 하나씩 사라지는 것(singularity가 없어진다)
Axis Angle
- axis angle, angle axis, rotation vector, rodrigues angle
- 물리학에서 벡터를 바라보는 방식으로 회전 표현
- 벡터 (방향 + 크기)
- 회전을 하는 축의 방향과 그 크기(각도) -> 축각도 (axis angle)
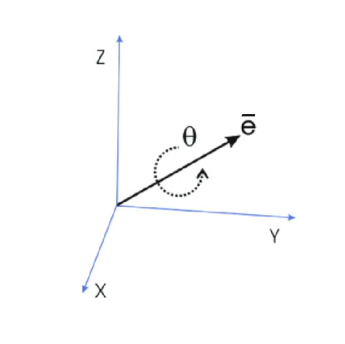
- rotation vector
- rotation axis : e (단위 크기)
- rotation angle : theta
- axis-angle <-> rotation matrix 변환
- 이 변환식을 rodrigues formula라고 한다
- axis-angle는 4개의 파라미터(또는 3개)로 회전값을 표현할 수 있어서 메모리 관점에서 좋다
- rotation matrix는 9개의 파라미터
Quaternion
- 4DoF 표현
- w,x,y,z
- 복소수를 사용하여 연속성 유지
- no singularity
- 미분이 가능 -> 최적화 가능 -> SLAM에서 사용 가능
- gimbal lock이 발생하지 않는다
SO(3) rotation matrix
-
Special Orthogonal Matrix(3D) -> SO(3)
-
회전을 시켜주는 matrix
-
기존의 x, y, z이 변환되어도 서로 수직을 유지해야 한다 (orthogonality 유지)
-
x, y, z의 determinant = 1
-
SO(3) * SO(3)_transpose = I
-
3축의 회전을 하나의 matrix로 표현할 수 있다. -> 9개의 파라미터(메모리를 잡아먹는다)
- x, y, z축의 회전을 먼저 생각하고
- 축마다 SO(3) rotation matrix를 만든 후
- 합성하여 하나의 matrix로 만든다
- R = Rz Ry Rx (x부터 순서대로 곱한다)

-
최적화가 어렵다
- SO(3) rotation matrix를 log map 또는 exponential map을 통해 lie algebra 공간으로 매핑
- lie algebra에서 미분가능하다
Metrix translation vector
- 벡터로 표현하는데 모든 축이 동일한 unit을 가지고 있으면 된다
- (x, y, z)
- mm? m? cm?
SE(3) Transformation matirx
- rigid motion을 하나의 matrix로 표현한 것
- SO(3) rotation matrix과 translation을 한번에 표현한 것
- 4x4 크기
- Special Euclidean Group(3D)
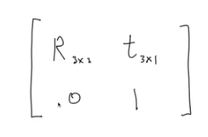
- R은 so(3) rotation matrix , t는 translation vector, 가장 오른쪽 원소를 1(1이면 유클리디언 스케일, 1이 없으면 프로젝티브 space) 로 하고 나머지는 0으로
Eigen을 이용한 rotation 표현
eigen matrix 초기화
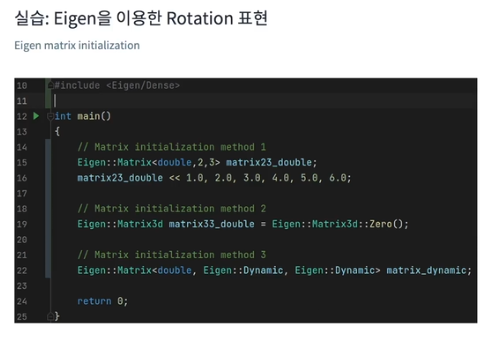
- 생성 후 초기화
- 생성할 때 바로 초기화 : Matrix3d는 double 3x3 의미
- 사이즈가 정해져있지 않은 matrix
eigen vector 초기화
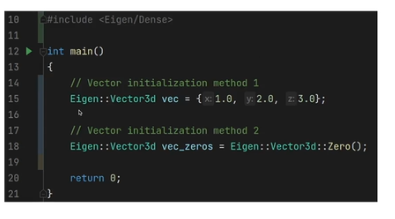
- vector3d : 3x1 double
element access
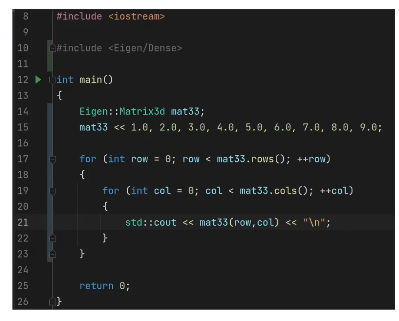
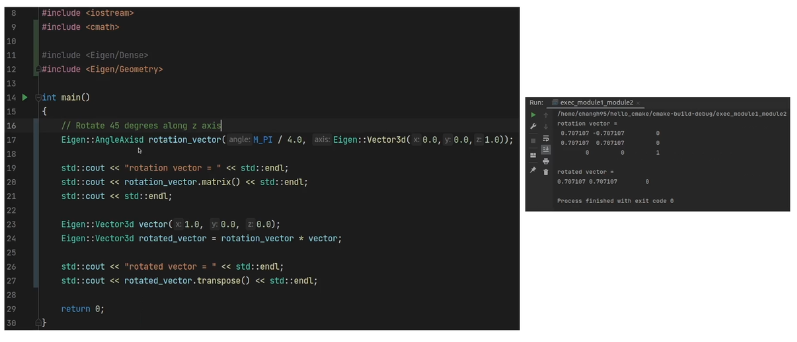
angle-axis
- #include <Eigen/Geometry> 필요
quaternion
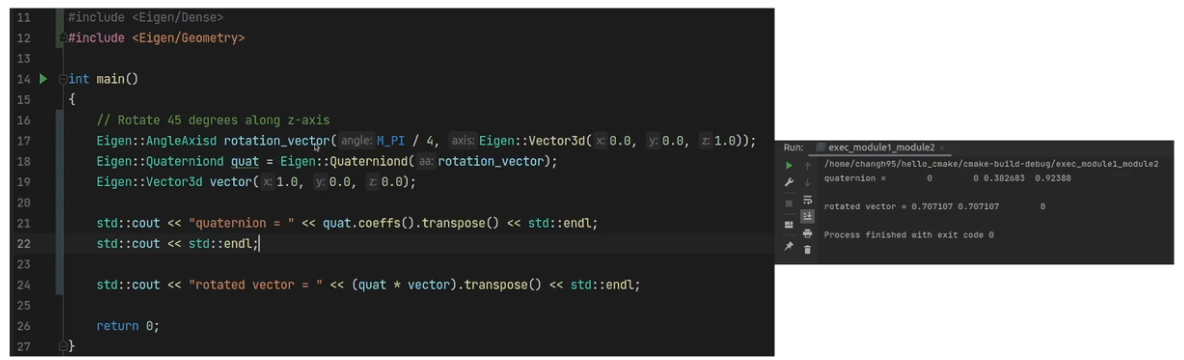
- transpose 이유 : 벡터 형태는 세로로 길기 때문에 가로로 보기 위해서
- *을 하면 알아서 복잡한 연산을 해준다
