[SLAM] 16. Perspective n points

1. Perspective n Points

PnP problem

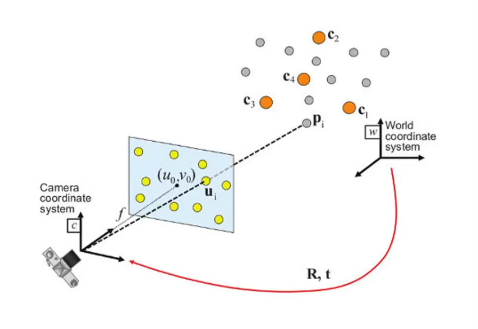
• 2D data와 3D data 간에 correspondence가 주어졌을 때 world coordinate system에서 camera coordinate system으로의 transformation (rigid body motion)을 추론하는 것이 목적!
• 현재 카메라 pose를 추정하는 것이 목적
• 이때 몇개의 2D to 3D correspondence를 사용했는지에 따라서 n의 숫자가 정해진다.

• PnP 문제는 왜 중요한가?
• 이미지에서 feature를 뽑고 map과 매칭함으로써 map에서 자신의 위치를 찾을 수 있게 해주는 중요한 기술
• localization과 직접적으로 관련있는 기술
• visual localization에서 PnP이 기술이 진짜 중요하다

• 3D point X에 연관된 descriptor는 오른쪽과 왼쪽 카메라에서 보인 descriptor 정보라고 할 수 있다
• PnP에서는 3D point X가 담고 있는 descriptor들과 현재 이미지에서 보이는 descriptor들을 매칭하여 2D to 3D correspondence를 구한다
• 충분한 수의 pair가 만들어지면 이를 통해 camera pose를 구할 수 있다

• PnP는 camera pose를 구하는 거니까 6DoF의 결과가 나타난다
• (tx,ty,tz,Rx,Ry,Rz) 값 : translation + rotation
• 6DoF를 구하기 위해서는 최소 6개의 데이터가 필요하다
• image feature $u_1$과 그에 해당하는 3D point $P_1$, 이렇게 (u1, p1), (u2, p2), (u3, p3) 3쌍 총 6개의 데이터 -> P3P가 minimum solver가 된다
• 하지만 P3P 알고리즘의 경우 noise를 고려하지 않는다
• 따라서 RANSAC과 같은 outlier rejection이 필요하다
• 그래서 보통 P3P를 사용할 때는 RANSAC framework에서 사용하는 경우가 많다

OpenCV 구현

• solvePnP()
• 데이터를 픽셀로서 계산하기 때문에 무조건 calibrated camera 즉 K matrix를 아는 경우에서만 사용 가능
• VSLAM에서도 pose tracking을 하기 위해 solvePnP()를 사용하기도 한다

---

2. Minimal solver - P3P Grunert method

• P3P를 푸는 방법은 다양하다
• 그 방법들은 모두 grunert 방법을 개선한 방법들이다

전제조건

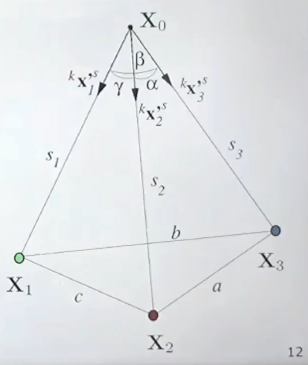
• world coordinate 기준으로 3D point인 X1, X2, X3의 위치를 알고 있다
• 카메라 이미지 위의 픽셀 x1', x2', x3' 위치를 알고 있다
• optical center(X0)로부터 픽셀 위치를 알고 있기 때문에 ray들마다의 각도를 계산할 수 있다
• 하지만 X0로부터 X1, X2, X3까지의 거리는 모르기 때문에 ray의 길이는 모른다

P3P 2 step process

1. projection ray들의 길이 추정
2. orientaion 추정

• 구하고 싶은 X1, X2, X3의 position 정보를 이렇게 표현할 수 있다
• s : ray의 길이 (scale)
• $^kx^s_i$ : object point를 향하고 있는 ray의 방향 벡터 (camera coordinate에서)
• R : world to camera coordinate transformation의 rotation 값
• $X_i - X_O$ : optical center와 point간의 거리값
• $R(X_i - X_O)$ : 3D world에서의 거리값이 camera coordinate에서 표현된다

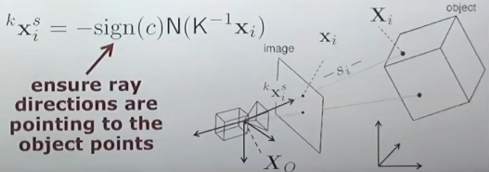
• c : camera constant (focal length = 이미지와 optical center와의 거리), 보통 이 거리를 이미지 센터에서 카메라 안쪽 방향으로 표현 (ray의 방향이 뒷쪽을 향한다)
• 그래서 sign(c)에 마이너스를 붙여서 -sign(c)로 사용
• N : normalization factor / x는 방향만 가진 단일 벡터가 되어야하기 때문에 normalize 수행
• $x_i$ : 실제 방향 표현, normalized된 이미지가 아니라 픽셀 단위
• 따라서 $K^{-1}$을 곱하여서 픽셀 단위에서 다시 normalize image plane으로 돌아가게 만든다

step 1 : projection ray의 길이 구하기

• s1, s2, s3가 알고싶은 ray의 길이

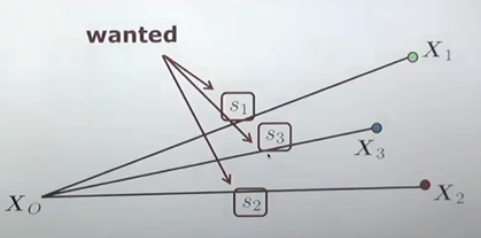
1. ray들 간의 각도 구하기
   

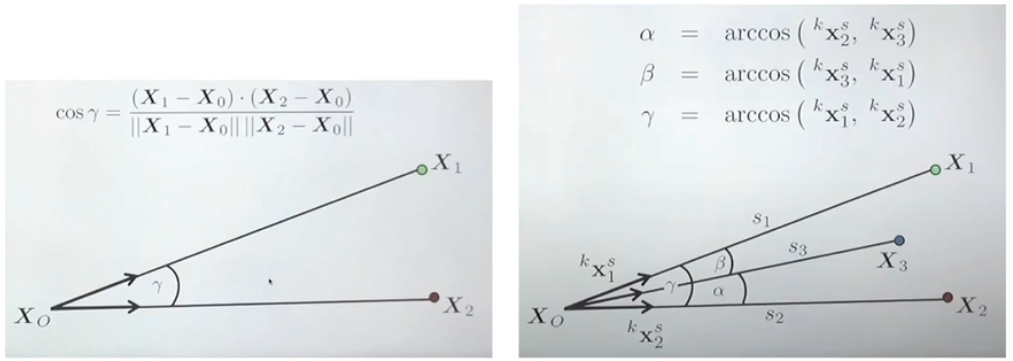
• 두 개의 line vector들을 dot product를 하면 cos세타를 구할 수 있다
• (X1-X0)를 통해 방향성을 얻는다
• 그 후 ||X1 - X0|| 길이를 나눠주면 단위 벡터를 얻을 수 있다
• 그 후 두 vector를 dot product를 하면 된다
• 이렇게 모든 x에 대해 구한 후 arccos을 통해 각도를 계산한다

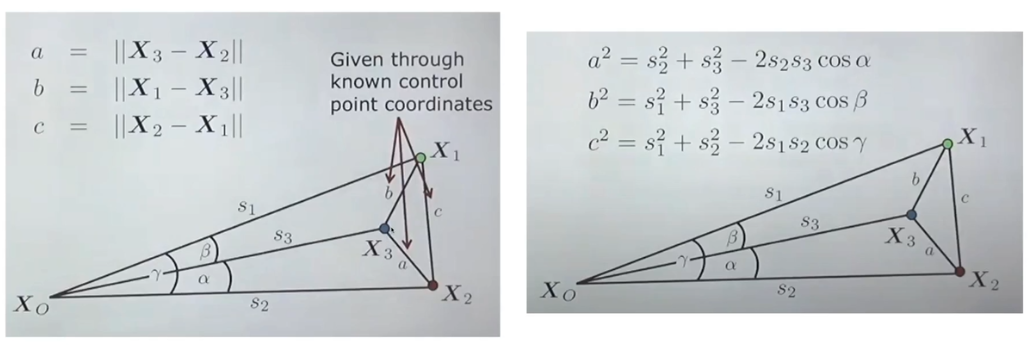
• X들의 3D 위치를 알고 있다 -> 3D point들 간의 거리를 알 수 있다
• 위의 그림처럼 만들 수 있는 삼각형에 cos 룰을 적용한다

• 이제 거리값을 구할 수 있다.
• 보기 쉽게 하기 위해 u, v를 정의하고 치환한다

• u을 중점으로 풀어주면 v만 남게된다
• 그 결과 4차 방정식이 생긴다
• 이를 풀면 s1, s2, s3에 대한 값을 구할 수 있다

step 2. : orientaion 추정

• 4차 방정식 -> 4가지의 solution이 나타난다
• 그 중 하나만 진짜이고 나머지는 무시해야하는 값
• 뭐가 진짜인지 어떻게 알 수 있나?
  • 다른 센서에서 획득한 orientation 정보를 prior로 사용하여 방향성을 검증 -> 다른 센서가 필요하다는 제약조건이 있다
  • 또다른 2D correspondence를 가지고 와서 그 point를 기반으로 방향성 검증
    • 장점 : 무조건 정확한 방향으로 s1, s2, s3를 구해서 카메라 pose를 안정적으로 구할 수 있다
    • 단점 : 하나의 데이터를 더 추가로 요구해야한다