[SLAM] 15. Triangulation

2D geometry 상황에서 feature correspondence를 통해 3D 공간을 재구성하는 방식을 배우고 추후에 mapping 기술을 익힐 수 있다

1. General Triangulation

triangulation이란?

• essential matrix와 fundamental matrix는 두개의 이미지 간의 상대적인 이동치를 추정하는 것이니까 위치추정과 비슷
• SLAM은 위치 추정과 매핑을 둘다!
• triangaulation이 매핑의 시작!

• 두개의 이미지 사이에서 상대적인 회전값을 알고 있고, feature들 간의 correspondence를 알고 있을 때 feature들이 의미하는 3D point X의 위치값을 복원하는 과정
• 2D에서 3D 공간으로의 매핑이 가능해졌다

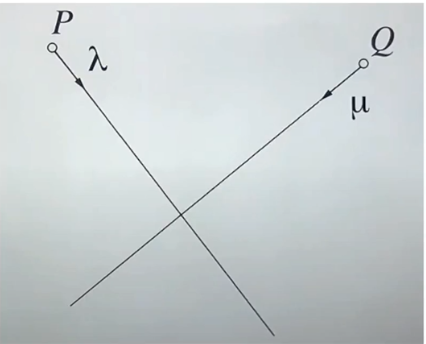
• 카메라 P와 Q가 있고 각각 3D point를 보는 ray가 있다
• 각각의 ray를 표현하는 파라미터 λ와 μ가 있다
• 이론적으로 이 두개의 ray는 3D point X에서 교차해야한다
• 하지만 실제 세상(3D)에서는 noise가 있기 때문에 교차하지 않는다! ray끼리 간격을 두고 떨어져있다

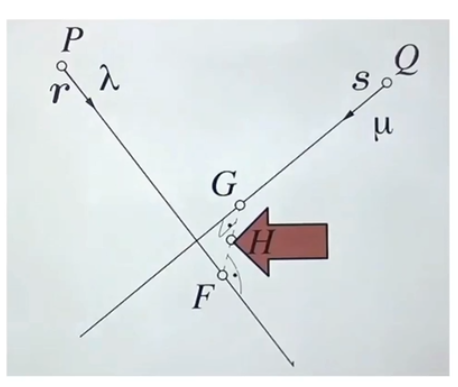
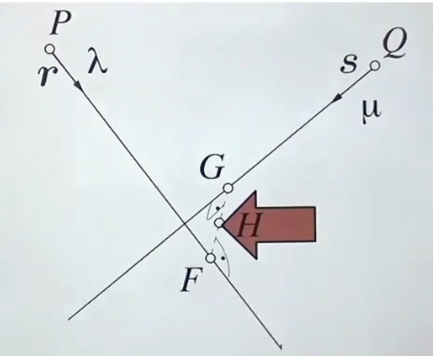
• 두 ray가 만날 수 있는 가장 가까운 점(G, F)를 찾고 이 점들 사이의 평균값(H)를 교차점으로 인식하는 방법이 있다
• 이 경우 P와 Q가 비슷한 정도의 노이즈를 가지고 있다는 전제가 있다

geometric solution

3D상에서 두 line을 표현하는 식

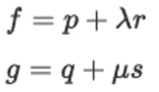
• P의 ray 표현 (f)
  • 방향 벡터인 r (단위 벡터)과 거리값을 나타내는 λ (scale)
  • 시작 위치를 나타내는 p (카메라 센터)
• Q의 ray 표현 (g)
  • 방향 벡터인 s과 거리값을 나타내는 μ
  • 시작 위치를 나타내는 q (카메라 센터)

F와 G의 위치를 알고 싶다

• F의 위치는 f식에서 p(시작위치)+λr(이동치)를 통해 구할 수 있다
• G의 위치는 g식에서 q(시작위치)+μs(이동치)를 통해 구할 수 있다

• p와 q는 알고 있는 값 / λ와 μ는 구하고 싶은 미지수 / r과 s는 구할 수 있는 값

direction vector 구하기 (r, s)

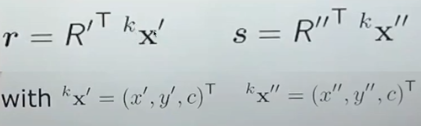
• kx'
  • k 즉 calibration이 된 카메라에서 왼쪽 카메라의 feature 위치
  • (x',y',c) -> x'과 y'은 위치, c는 camera constant(focal length 의미)
• kx" : calibration이 된 카메라에서 오른쪽 카메라의 feature 위치

• R : rotation matrix (world -> camera 즉 3D 세상 속의 camera이 위치)
• SO(3) matrix에서 transpose는 inverse를 의미한다. 그럼 $R^T$ 는 camera->world transformation
• $R^T$에 2D위치인 x'를 곱해주면 카메라 space의 feature가 world로 가게 되니까 world coordinate에서 표현한 3D ray가 된다.
• r과 s 모두 3D world 상에서 표현되는 direction vector가 된다

• 이제 p, q, r, s를 알게 되었다
• 하지만 여전히 이 두 수식으로는 바로 intersection(교차점)을 구할 수 없다
• 두 개의 ray는 intersect하기 않기 때문이다
• 이제 H를 알고 싶다

H 구하기

• 알고있는 기하학적 특성
  • G와 F는 P와 Q가 가장 가깝게 거리를 가지는 지점
  • 즉, FG 벡터는 P, Q에 대해 orthogonal(수직)하다

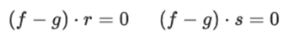
• 수직인 벡터끼리 dot product를 수행하면 0 (cos90을 하면 0이니까)

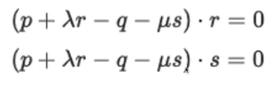
• 앞에서 정의한 f, g을 대입
• 각각 P, Q의 ray에 대한 식이 된다
• 두 개의 수식으로 두개의 미지수(λ와 μ)를 풀면 된다
• 그럼 λ와 μ를 구할 수 있고 이를 f, g 수식에 대입 -> F, G 위치 구하기 -> FG 직선의 중간값을 구하면 3D point H의 위치를 구할 수 있다

orthogonal projection

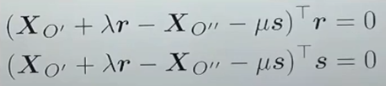
• p, q로 표현하던 camera center를 실질적인 카메라 위치인 $X_{O'}$ (왼쪽 camera center)와 $X_{O"}$ (오른쪽 camera center)로 표현
• 위의 식을 풀어주면 아래와 같이 된다. 이때 camera center에 대한 항들을 묶어준다

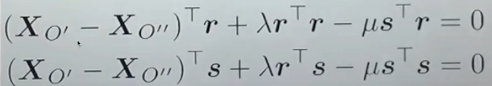
• $(X_{O'}-$X_{O"})$ 는 카메라 간의 상대적인 이동거리 의미
• 한번 더 정리하면

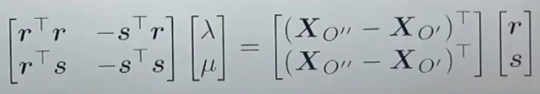
• 이 수식은 Ax = b의 형태를 띄고 있다
• 알고있는 A, b와 구하고 싶은 미지수 x (λ와 μ)
• 바로 미지수를 구할 수 있다
  $Ax = b$
  $A^{-1}Ax = A^{-1}b$
  $x = A^{-1}b$

• 이렇게 미지수를 풀면 λ와 μ를 구할 수 있고 F,G를 구할 수 있고 H를 구할 수 있다
  

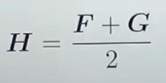
• 의미를 살펴보면 F의 영향도가 0.5, G의 영향도가 0.5라고 볼 수 있다

• 고도화된 알고리즘에서는 P와 Q의 위치를 수정할 때 나타나는 확률을 기반으로 uncertainty(불확실성)를 구할 수 있다. 이 값에 따라 F와 G의 신뢰도가 달라지고 H를 구하는 weight가 달라지기도 한다

---

2. Stereo Triangulation

• 전방 stereo 카메라

visualization

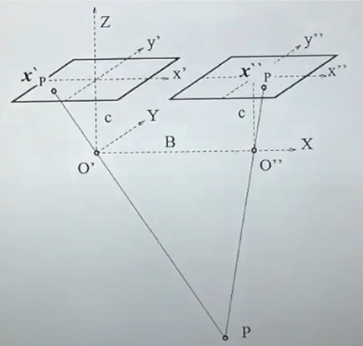
• 좌우 카메라가 둘다 전방을 바라보고 있고 같은 plane에 위치해 있다
• 둘 간의 baseline, x', x"의 위치를 알고 있다
• 두 개의 이미지에 있는 feature의 위치의 차이를 알고 있다
  • 이 차이를 disparity 또는 parallax라고 한다

top view projection

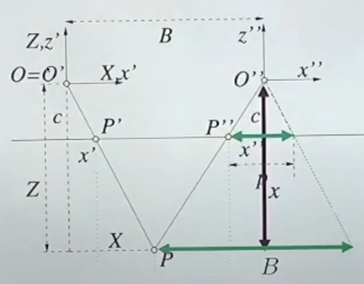
• O', O" : optical center
• P : 3D point
• P', p" : 이미지에 맺힌 상
• B : baseline 거리, 두 카메라 간의 거리

• 왼쪽의 ray(O'과 P의 line)을 오른쪽 O"에 붙인다
• 삼각비를 활용하여 Z값을 계산할 수 있다
• 알고 있는 값들
  • c : camera constant (카메라와 이미지간의 거리)
  • B : baseline 거리
  • disparity 값 : P'과 P" 간의 거리

Z 좌표 구하기

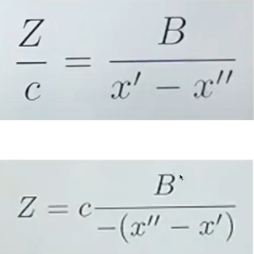
• B와 c는 상수이다 -> disparity만 계산하면 Z를 알 수 있다

X 좌표 구하기

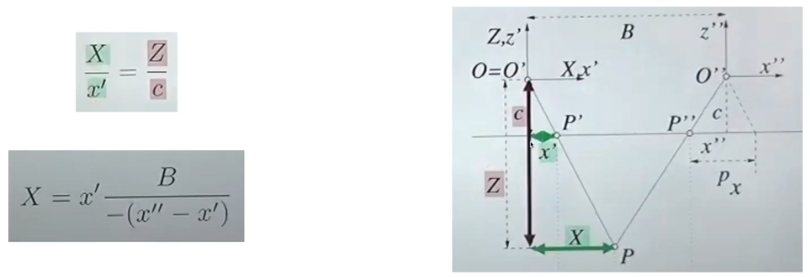
• 비슷한 방법으로 X 좌표도 알 수 있다
• Z를 모르는 상태여도 앞의 수식을 활용해서 구할 수 있다

Y 좌표 구하기

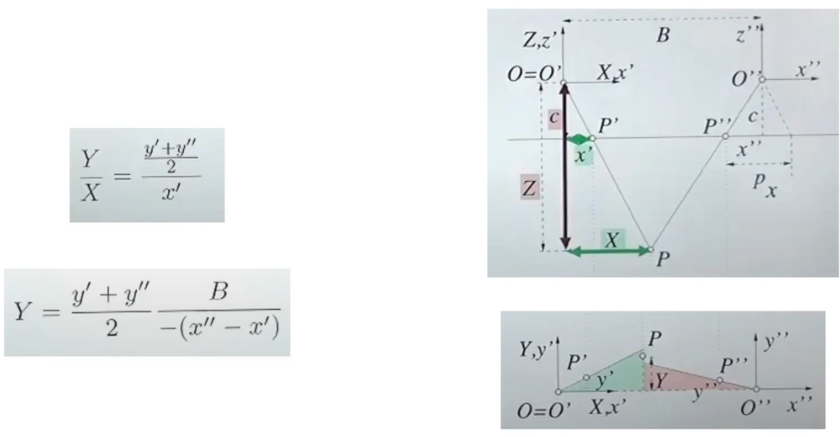
• Y 좌표도 구할 수 있다.
• 하지만 실제로 아까와 같은 방법으로 구할 수 없다
• why? noise로 인해 ray가 교차하지 않을 수 있기 떄문
• X와 Z가 완벽하게 맞아 떨어지면 Y가 맞지 않을 수 있고, Y와 Z가 완벽하게 맞아 떨어지면 X가 맞지 않을 수 있다
• 왼쪽에서 보는 y값(y')과 오른쪽에서 보는 y값(y")의 평균값으로 계산하면 된다