[SLAM] 17. 최소자승법

1. Least squares (최소자승법)

• SLAM의 목표
  • 동시적 localization and mapping
  • 최적의 odometry와 map을 동시에 계산하는 것이 목표

Least squares이란?

• 최적의 방법을 찾는 방법 중 하나
• $error^2$ 을 사용
• over-determined system의 해를 푸는 방법
• over-determined system : 미지수의 개수 < 방정식의 개수
• SLAM은 항상 over-determined system : landmark, camera pose 보다 센서의 데이터가 항상 많기 때문이다

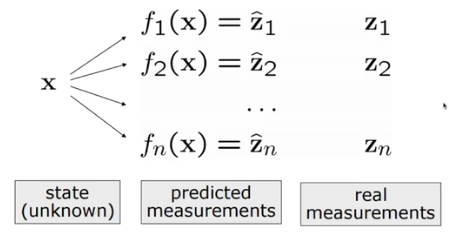
• $x$ : 추정한 state
• $z$ : real sense measurement
• $f(x)$ : sensor 값 추정 식
• $\hat{z}$ : 추정한 sensor의 값
• x는 제대로 추정했다면 z가 어떤 형태로 나와야하는지 알 수 있다
• $z$와 $\hat{z}$는 차이가 있을 수 있다 -> error가 존재
  • sensor noise
  • 수식 상의 모델링 에러
• least quares = $z$와 $\hat{z}$의 합이 최소가 되는 x 값을 찾아내는 것

---

2. Maximum-a-posterioir (MAP) estimation in SLAM

Motion / Observation model

Motion model

• 현재의 위치와 관련된 state를 추정할 수 있게 해주는 수식
• proprioceptive sensing의 수식

• $x_{k-1}$ : 이전 프레임의 state
• $u_k$
  • control 또는 odometry
  • 이전 state와 현재 state의 차이
  • control : 제어의 관점 / 전방으로 0.5m 움직여라 같은 명령을 내렸을 때
  • odometry : 측량의 관점 / odometry 센서가 0.5m 움직였다라고 센서 값을 받았을 때
• $\epsilon_u$ : motion noise
• 즉 현재 state = 이전 프레임 state + 이동치 + 노이즈값

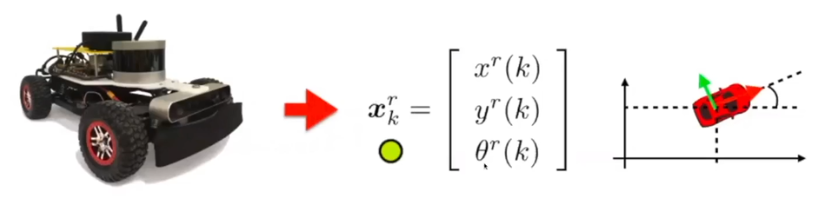
• 자이카는 평명에서 이동하는 wheel odometry를 사용
• state는 x좌표, y좌표, θ로 표현할 수 있다
• 각각의 시점마다 state가 존재한다
• (0,0,0) + (1,1)만큼 움직이고 45도만큼 회전해라(control input)
• 여기에 노이즈가 끼면 (1.1, 1.1, 50도)라고 할 수 있다

Observation model

• landmark의 위치와 관련된 state을 추정할 수 있는 수식
• exteroceptive sensing의 수식

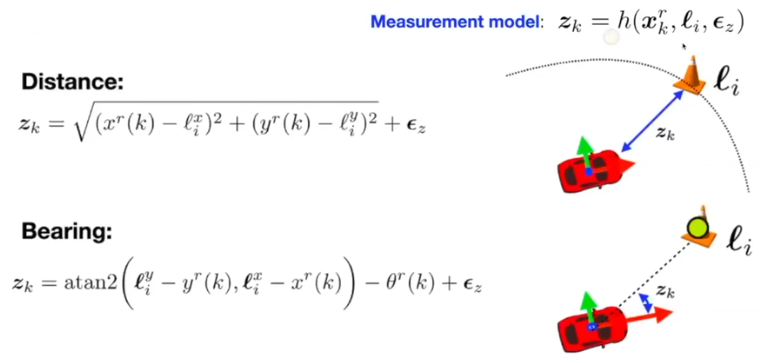
• $x_{k}$ : 현재 state
• $l_i$ : 랜드마크 state, 랜드마크의 상대적인 위치
• $\epsilon_z$ : 센서 노이즈

• LiDAR를 사용한다고 하면 distance값과 bearing값을 사용할 수 있다
• distance : 로봇과 랜드마크의 거리
• bearing : 로봇과 랜드마크의 상대적인 방향 변화

SLAM State and Uncertainty

• SLAM은 각 시점마다 state를 가지게 되는데 SLAM에서 state는 한개의 로봇 pose와 다수의 관측가능한 랜드마크의 state를 가지고 있다.
• SLAM state = 1개 robot motion state + 다수의 landmark state
• 노이즈를 확률적으로 분석하여 최적의 로봇 pose와 landmark position을 계산하는 것이 SLAM의 목적
• 하지만 motion과 observation 모두 노이즈가 있기 때문에 어렵다
• 시간이 지나면서 motion과 observation에 대한 수식이 많아질수록 노이즈가 누적된다 = state uncertainty가 시간이 지나면서 늘어난다
  

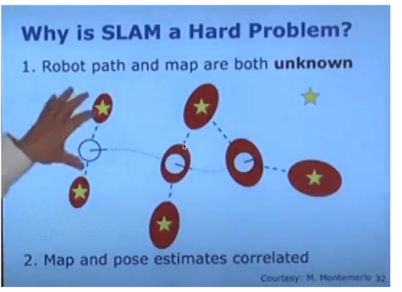
• 빨간색 -> 노이즈 포함
• 별 : observation
• 동그라미 : 위치
• 첫번째 pose는 이동치가 없으니까 motion 노이즈는 없고 observation 부분에는 노이즈가 있다
• 이동 후 : motion 노이즈 추가
• 이동하면서 점점 노이즈가 추가되어 uncertainty 증가
• 이 증가하는 uncertainty를 해결하는 방법이 있다 -> loop closure (이건 이따가 다룬다)

Maximum-a-posterior(MAP) Estimation

• 노이즈 패턴을 분석하면서 최적의 로봇 pose와 landmark position 값을 얻는다
• motion model과 observation model의 정보를 기반으로 노이즈에도 최적의 값을 구하는 것 = belief
• 실제 센서 데이터는 관측 후에 나타나는 어떠한 결과 즉 사후 데이터이기 때문에 사후 데이터를 가장 잘 표현하는 확률을 찾는다 즉, 최대 사후 확률(MAP)을 구한다

MAP 푸는 방법

• motion와 observation의 확률 분포를 찾고, 이 확률 분포를 정확하게 표현하는 state의 값을 찾는 것이 목표

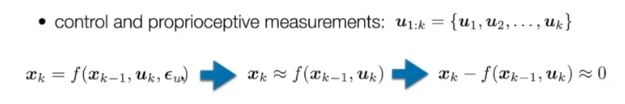
• motion model
• 노이즈 $\epsilon_u$ 가 0에 수렴한다는 가정
• 이전 state값에 이동값을 더하면 현재 state가 나와야한다
• $\epsilon_u$ 가 0에 수렴하게 되니까 이 값이 x-f(x,u)와 동일하다고 볼 수 있다

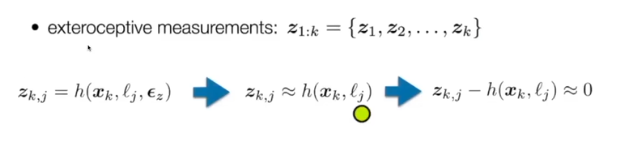
• observation model
• $\epsilon_z$가 0에 수렵한다는 전제

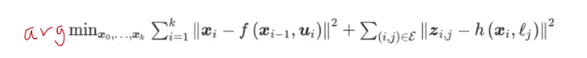
• 두개의 $\epsilon$이 최소화되는 지점을 찾는 것이 목표
• argmin : 식이 최소화가 되는 파라미터가 되는 값들을 찾으려고 한다
• 왼쪽항 : motion model의 e값의 제곱 -> Least squares에서는 에러를 제곱 -> 모든 케이스에 대해 합
• 오른쪽항 : observation model의 e값의 제곱의 합
• 전체 : motion model의 total error + observation model의 total error -> total error
• argmin(total error) : total error가 최소화되는 state 구하기

Motion-model only

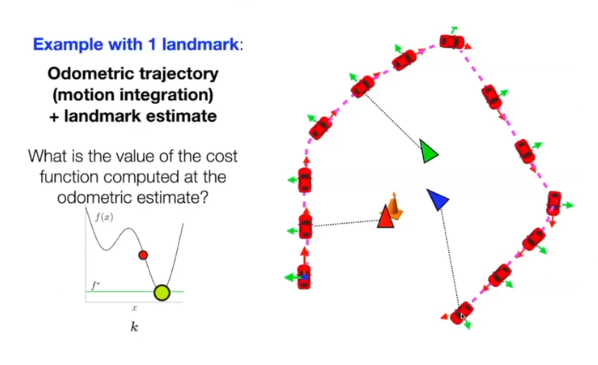
• motion model error만 최적화했다고 하자
• 그 후 landmark의 위치를 추정하면 동일한 위치가 아니다

motion model + obsevation model

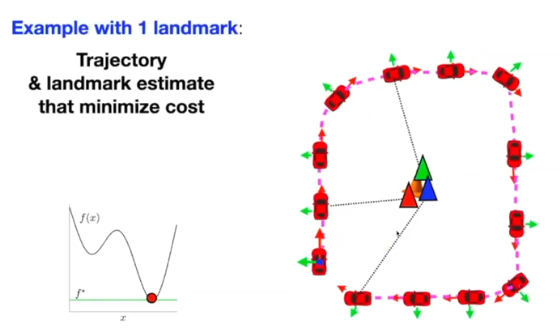
• 둘다 정확해졌다
• 노이즈를 완벽하게 제거하지는 못했지만 최소화된 에러를 가지는 state들을 계산했다
• 최적화 수식에 motion와 obsevation 둘다 넣어서 동시에 최적화시켰기 때문에 가능

• 여러개의 cost function을 한번에 최적화해서 state 구하는 것 (여러 파라미터 동시 최적화) = joint optimization
• SLAM : 동시적 위치추정과 mapping을 할 수 있는 이유 (한번에 최적화)

---

3. Graph-based SLAM

SLAM의 2가지 방법론

• incremental SLAM (online SLAM)
  • 주로 filter 기반 알고리즘이 사용되는 경우가 많다
  • particle filter, extended kalman filter
  • batch SLAM 보단 빠르지만 drift error에 취약하고 부정확하다
• batch SLAM(offline SLAM)
  • graph 최적화 알고리즘이 사용되는 경우가 많다
  • graph-based SLAM
  • batch의 grapy 최적화 방법론이 incremental의 필터 방식보다 효율적이다 -> 대부분의 VSLAM에서 batch 방법 사용

incremental SLAM

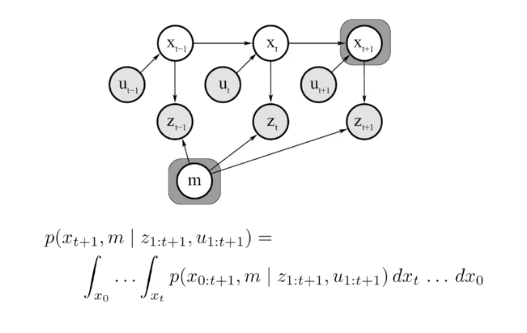
• 가장 최종 state만 추정한다
• 기본 전제 조건 : markov chain assumption
  • 이전 state들의 정보는 지속적으로 새로운 state에 녹아든다
• 새로운 state 계산 = 이전 state + control input + observation 정보만 있으면 된다
• 계산에 들어가는 정보가 적어서 빠르다 -> 실시간으로 사용할 수 있다는 의미로 online SLAM이라고 한다

Batch SLAM

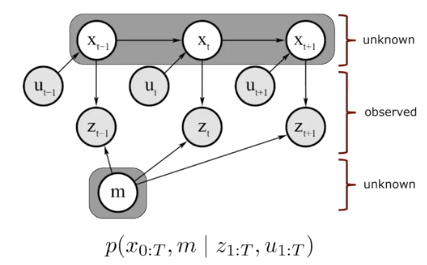
• 여러 시점의 state를 한번에 추론
• 동시에 여러 시점의 정보를 독립적인 확률 분포를 가지고 추론 -> state간의 drift 에러는 해소된다 (drift error : 누적 에러)
• 많이 정보를 계산해야하기 때문에 속도가 느리다
• 하지만 현대 SLAM에서는 batch SLAM도 실시간으로 사용할 수 있다

Factor graph

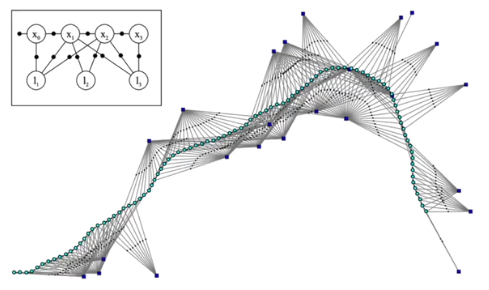
• SLAM의 graph를 다루는 방식
• node와 edge로 이루어진 그래프
  • node : robot state, landmark state 정보가 저장되어 있다
  • edge : motion model의 정보(motion constraints), observation model의 정보(observation constraints)가 저장되어 있다
• edge에 저장되는 내용을 factor라고 부른다

• 그래프를 최적화한다 = 특정 node에 연결되어있는 factor의 에러치를 이용하여 최적화한다

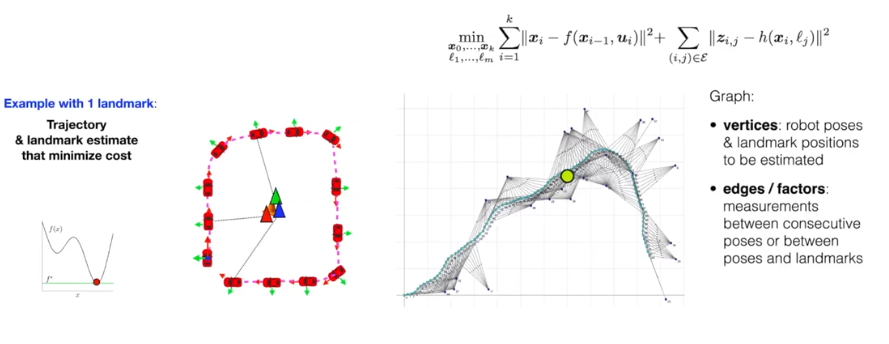
Graph-based SLAM

• factor graph 사용이 보편화되면서 Graph-based SLAM이 주로 VSLAM이 사용하는 방법이 되었다
• Graph-based SLAM을 통해 SLAM의 Least squares를 쉽게 적용할 수 있게 되었다
• 장점
  • robot pose와 observation에 대한 링크를 쉽게 파악할 수 있다
• 그래프 안에 loop가 생기게 되는 경우 loop에 대한 graph 최적화를 함으로써 loop 속에서 누적된 uncertainty를 제거해주고, loop 안의 모든 node들에 대한 최적화된 값을 찾을 수 있게 되었다 -> loop closure
• loop closure를 통해 노이즈를 효과적으로 제거할 수 있게 되었다

program flow of graph-based SLAM

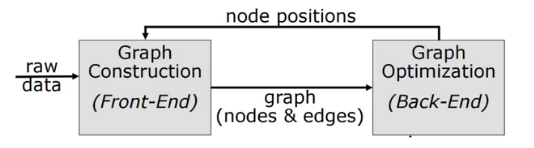
• SLAM에도 pipeline이 생기게 되었다
• frontend
  • 그래프의 새로운 node와 edge를 추가해주는 작업
  • feature를 뽑고 relative를 구하고 triangulation 등등
• backend
  • loop closure, 그래프 최적화 알고리즘 수행

Visual-odometry vs Visual-SLAM

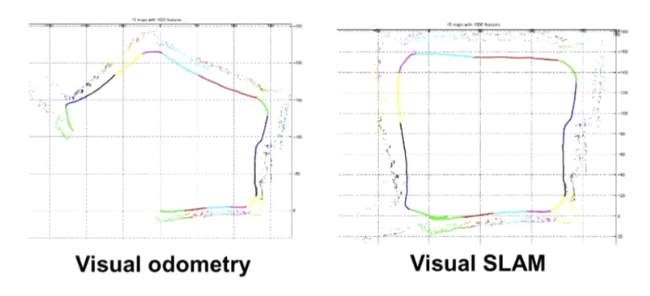
• Visual-odometry

  • 누적되는 drift를 직접 제거할 수 있는 방법
  • global graph optimization을 할 방법이 없다

• Visual-SLAM

  • 누적되는 drift를 제거할 수 있는 방법 즉, loop closure 방법이 있다
  • global graph optimization 포함

Visualization of graph-based SLAM