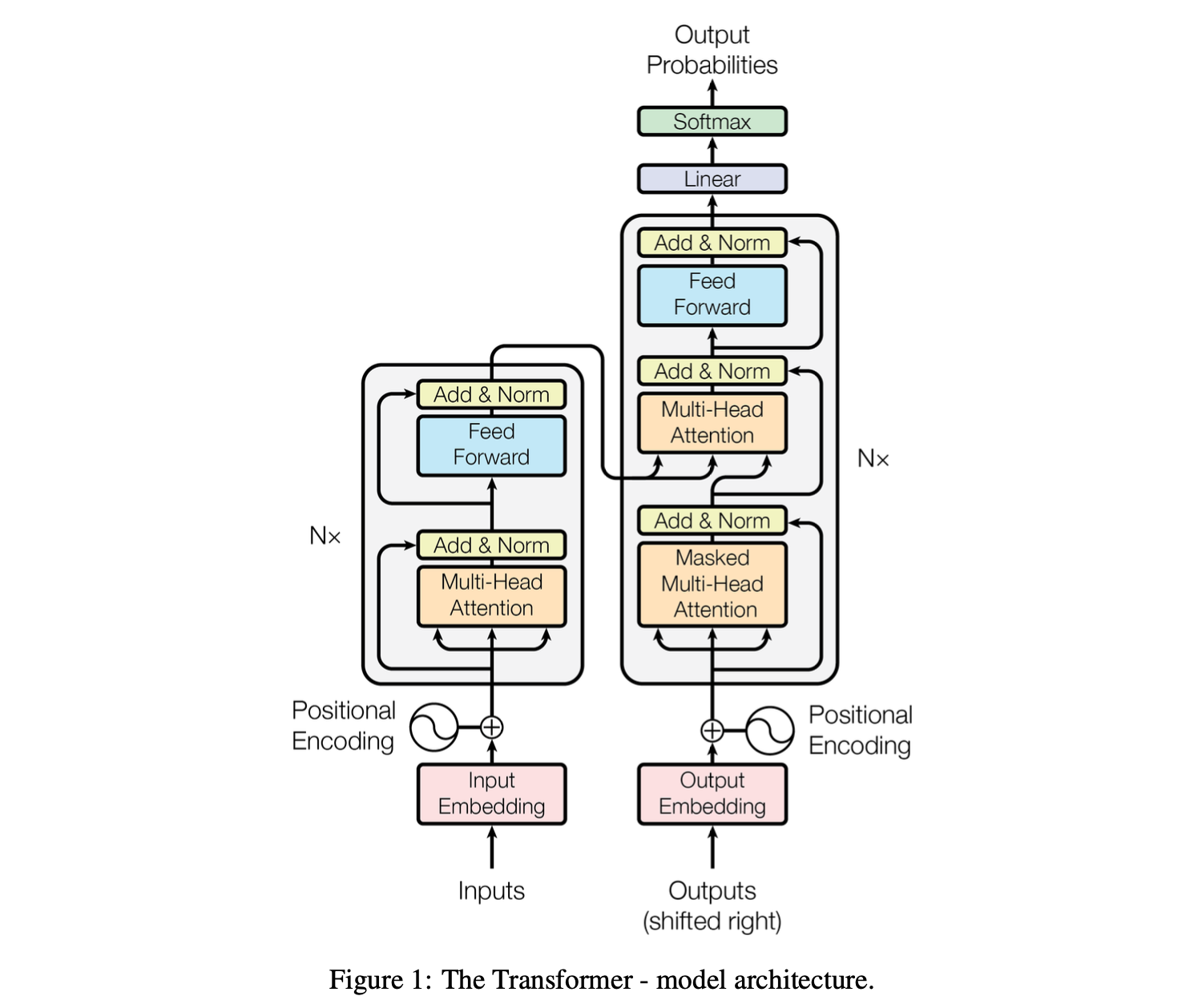
abstract
대부분 시퀀스 변환 모델은 RNN/CNN 기반 인코더-디코더 구조. 가장 성능 좋은 모델도 어텐션 메커니즘으로 인코더-디코더 구조
→ 더 심플한 트랜스포머 구조 제안. Recurrent/Convolution 연산 배제
2개 기계 번역 테스크에서 병렬화, 학습 시간 줄이는데 아주 좋아요
8개 GPU로 3.5일 동안 훈련해서 WMT 2014 SOTA 찍음. 우리가 짱
Instruction
RNN/LSTM/gated-RNN이 그 동안 시퀀스 모델링/변환 문제에서 짜세였음. 많은 사람들이 도전했었음.
RNN의 문제점: 기억력 이슈로 example 간 배치 연산 제한됨 ⇒ 병렬화 안 됨. 최근(2017) 연구 중, factorization, conditional computation 등 일부 발전함 → 하지만 시퀀스 연산에서 제한은 여전히…
- 왜 메모리 제한됨?(기억력을 메모리로 착각한 이슈) 메모리가 아니였음(현재는 수정함) 복습할 겸 다시 적자면, hidden 값 다음으로 넘겨주면서 기울기 소실/폭발 문제 발생함! → 넌 왜 항상 그런 식이야? 🥵
어텐션 매커니즘: RNN과 함께 사용됨
반복 피하고 입/출력 종속성을 줄이기 위해 트랜스포머 만들었음. 트랜스포머는 병렬화할 수 있고 GPU 8개 12시간으로 학습해도 번역에서 SOTA임.
Background
시퀀스 연산 줄이려는 시도: Extended Neural GPU, ByteNet, ConvS2S → CNN을 기본 블록으로 사용, 입출력 hidden 계층을 병렬로 연산
위치에 따라 연산량이 ConvS2S에서는 linear, ByteNet에서는 지수적으로 증가 → 멀리 떨어져 있는 시퀀스 학습 힘듦 vs 트랜스포머에서는 일정함
트랜스포머에서 attention 계수에 따라 effective resolution이 낮아짐
- effective resolution 설명
 출처: https://yonghip.tistory.com/entry/%EB%B6%80%EC%8A%A4%ED%8A%B8%EC%BA%A0%ED%94%84-Transformer-%EC%A0%95%EB%A6%AC
출처: https://yonghip.tistory.com/entry/%EB%B6%80%EC%8A%A4%ED%8A%B8%EC%BA%A0%ED%94%84-Transformer-%EC%A0%95%EB%A6%AC
effective resolution이 낮아지는 현상을 Multi-Head Attention으로 해결
Self-attention(intra-attention)은 시퀀스 내 attention임. 시퀀스 내 위치를 연관지어서 시퀀스 표현을 계산함
- 개인적인 재해석
- 원문: Self-attention, sometimes called intra-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence.
- 트랜스포머 구조: 인코더 6개 계층 - 디코더 6개 계층
- 각 계층에서 attention value/context vector를 연산할 때 현재 시퀀스, 즉 자기 자신을 사용
- 현재 시퀀스/자기 자신: 인코더의 경우 입력, 디코더의 경우 현재까지 출력(미래 참고하면 안 되니깐)
- 시퀀스 내 위치를 연관짓는다 → attention value/context vector 구하기
- 시퀀스 표현을 계산 → context vector와 현재까지 시퀀스 각 계층에서 다음 단계로 넘겨주는 행위 가 아닐까라는 생각. 이 부분에 대해서는 이야기 나눠보면 좋을 듯!
Self-attention은 독해, 요약, 텍스트 함의, 문장 표현 학습에서 짱짱맨
- 텍스트 함의, 문장 표현 학습(Text entailment, Task-independent sentence representation)
- 텍스트 함의: 전제 문장이 있는 경우, 결론 문장을 추론하는 작업
 출처: https://en.wikipedia.org/wiki/Textual_entailment
출처: https://en.wikipedia.org/wiki/Textual_entailment
- 문장 표현 학습: 문장을 고정된 크기의 벡터로 표현하는 방법(의미에 따른 임베딩)

- 텍스트 함의: 전제 문장이 있는 경우, 결론 문장을 추론하는 작업
End-to-end 메모리 네트워크: recurrent attention에 기반함 → 그리고 단순한 QA와 language modeling에서 좋았음!
- 개인적인 재해석 + 논문 참고 End-to-End: 별도 피처 엔지니어링 없이 입력에서 출력까지 학습 가능한 방식. attention과 memory를 결합. step 1. 입력 데이터를 외부 메모리에 저장함. step 2. 질문이나 작업 들어옴. step 3. 여러 번의 메모리 접근(memory hop이라고 하네요.)으로 답변
→ 모델 전체(end-to-end)가 학습. 감독 없이도 효과적이라고 합니다. 하나의 손실 함수만 사용한대요. https://arxiv.org/abs/1503.08895?utm_source=chatgpt.com
그러나! 트랜스포머는 최초의 변환(transduction) 모델임. RNN, 콘볼루션 사용 안 함.
- 변환을 “transduction”이라고 자꾸 표현한 이유. https://en.wikipedia.org/wiki/Transduction_(machine_learning)
 transduction는 특수한 케이스 → 특수한 케이스로 대응하는 reasoning이다. conversion이 아닌 이유: conversion은 바뀌는 과정이 단순한 경우에 사용하기 때문. 트랜스포머 작동을 간단하게 설명하면 입력 시퀀스 넣으면 출력 시퀀스가 나오는데, 이는 AI 처음 배울 때 나오는 회귀(Regression)와 다름. 회귀는 입출력 형식(차원)이 정해져 있는 반면, 트랜스포머는 입출력 형식이 정해져 있지 않음. 따라서 입력을 넣으면 출력으로 ‘변환’된다고 표현하는 듯. 우리 STS 강의에서 했던 N21, N2M 생각해보면 좋음. 문장마다 다른 토큰 개수 맞추기 위해 임베딩을 Collation하지만, 본질적으로는 문장마다 ‘특수한’ 케이스를 출력하므로 트랜스포머를 transduction 모델이라고 지칭하는게 아닐까 싶음.
transduction는 특수한 케이스 → 특수한 케이스로 대응하는 reasoning이다. conversion이 아닌 이유: conversion은 바뀌는 과정이 단순한 경우에 사용하기 때문. 트랜스포머 작동을 간단하게 설명하면 입력 시퀀스 넣으면 출력 시퀀스가 나오는데, 이는 AI 처음 배울 때 나오는 회귀(Regression)와 다름. 회귀는 입출력 형식(차원)이 정해져 있는 반면, 트랜스포머는 입출력 형식이 정해져 있지 않음. 따라서 입력을 넣으면 출력으로 ‘변환’된다고 표현하는 듯. 우리 STS 강의에서 했던 N21, N2M 생각해보면 좋음. 문장마다 다른 토큰 개수 맞추기 위해 임베딩을 Collation하지만, 본질적으로는 문장마다 ‘특수한’ 케이스를 출력하므로 트랜스포머를 transduction 모델이라고 지칭하는게 아닐까 싶음.
Model Architecture
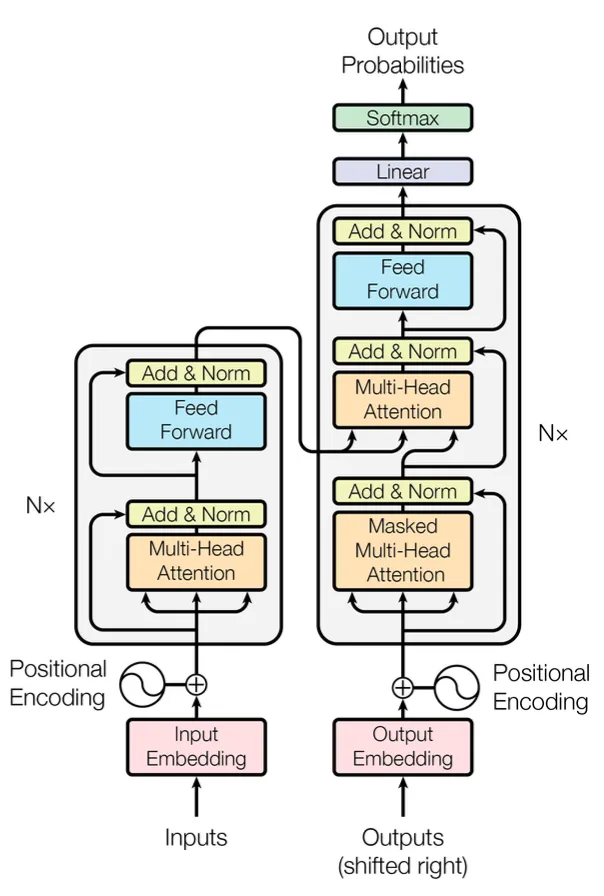
3.1 Encoder and Decoder Stacks
Encoder
- 모든 층이 똑같은 6층
- 각 층은 2개의 세부 층으로 나뉨
- multi-head self-attention(이하 MHA)
- fully connected feed-forward (neural) network(이하 FFN)
- 각 층에 Residual connection 이후 Layer Normalization
- Residual connection 위해서
Decoder
- 6층이고요
- 디코더에서 MHA → 인코더 층 출력과 같이 MHA → FFN
- residual connection, layer normalization
- 디코더 MHA에서는 이전 출력만 참고하도록 마스킹
3.2 Attention
- TMI: 제 노래 취향은 Attention < Super Shy임니다. 노래 추천 시 참고 바람.
attention 함수는 query, key-value 쌍, output으로 표현됨. 전부 벡터임. query, key로 계산된 계수로 value를 weighted-sum.
3.2.1 Scaled Dot-Product Attention
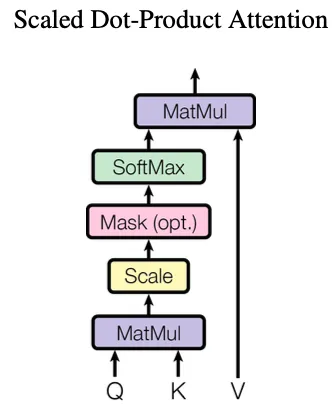
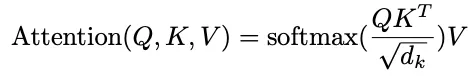
query, key의 차원: , value의 차원:
query * key 하고 로 나누고 softmax 취해서 value 곱함
query 묶어서 Q라는 행렬로 표현. key, value도 각각 K, V로.
가장 흔하게 쓰이는 attention 함수는 additive attention, dot-product attention임. dot-product와는 스케일링 인자를 가지는 것 이외는 전부 동일.
Additive attention은 1개 은닉층으로 구성된 FFN를 사용해서 함수(compatibility function)을 계산함
Dot product attention과 Additive attention은 복잡도가 똑같으므로(로 동일. 행렬 곱 연산에서 복잡도 참고.) Dot product가 빠르고 공간을 덜 차지한다.
- 행렬 곱 코드(numpy)는 최적화가 잘 되어 있음.
- Additive attention은 행렬 곱 연산만 하지 않음. 따라서 최적화 영향 덜 함
가 작은 경우에는 두(dot product, additive) 어텐션이 비슷하게 동작하지만, 가 큰 경우에는 additive < dot-product. additive에서 소프트맥스 연산 사용.
반면, dot-product에서 값이 클 수록 소프트맥스 함수를 완전 작은 그래디언트로 만듦. dot-product 결과가 additive로 들어가기 때문에 로 스케일링 함.
3.2.2 Multi-Head Attention
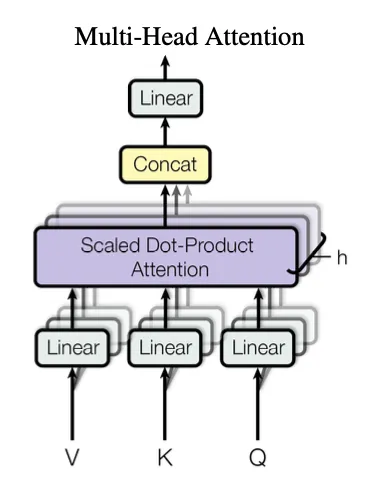
쿼리, 키, 값을 학습 가능한 선형 변환(여기서는 행렬 이 학습 대상)을 차원으로 번 투영한게 더 좋음.
- 여기서 투영은 선형대수에 나오는 개념. 사영(projection) 떠올릴 것.
각 투영된 쿼리, 키, 값을 병렬로 수행 → 헤드마다 독립적으로 어텐션 수행 → 헤드 별 representation subspace 정보 학습 가능
- 헤드 별로 다른 관점으로 정보를 학습 가능하다는 이야기
헤드 별 출력을 concat함 → 다시 투영. 이때도 선형 변환으로 투영하는데, 학습 대상은
멀티 헤드의 이점 다시 정리: 헤드 별로 다른 representation subspace에서 다양한 위치와 정보를 동시에 주목(attend)! 단일 헤드는 이를 방해함.
- 내 예시: 하나의 헤드는 전체 의존성(위치, 단어 등)을 학습. 멀티 헤드는 각 헤드가 따로 의존성을 학습해 취합.
헤드는 8개. 따라서 헤드 별 차원은 를 8개로 나눈 64
- further question: 왜 h=8인가? → 논문 후반부에서 설명!
전체 계산량은 동일하지만, 헤드 별로 따로 attention 학습
3.2.3 Applications of Attention in our Model
Encoder-Decoder Attention
쿼리는 이전 디코더 층에서, 메모리 키와 값은 인코더 출력에서 온다. (정확히는 ‘쿼리들, 키들, 값들’)
디코더에 모든 위치가 입력 시퀀스 모든 위치를 attend 하도록 → 전형적인 encoder-decoder attention 모방
Encoder Attention
키, 값, 쿼리가 이전 인코더 층 출력에서 온다. 현재 인코더 위치 별로 이전 인코더 위치 전체를 attend 하도록
Decoder Attention
인코더 어텐션과 비슷: 현재 디코더의 위치 별로 이전 디코더 층 위치 전체를 attend 하도록
하지만 auto-regressive 특성을 살리기 위해 미래(논문 표현 leftward) 정보 참조를 방지함 → scaled dot product 어텐션 내부에 미래 정보를 음의 무한대로 마스킹 → 소프트맥스 입력에서 미래 정보 참조 막기 위함
3.3 Position-wise Feed-Forward Networks
인코더/디코더에 FFN → 각 위치를 따로, 동등하게 적용함
선형 변환 - 렐루 - 선형 변환
- 선형 변환 하나만 두고 렐루 변환하면 안 됨? 차원을 늘렸다 줄이기 위함 → 모델이 더 복잡한 패턴을 학습하도록 출처가 정확하지 않아서 다시 생각해야 함: https://hazel-nut-library.tistory.com/entry/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0-Attention-is-All-You-Need-Transformer?utm_source=chatgpt.com
층 별로 가중치 다름.
FFN을 다르게 표현하는 방법: 커널 크기가 1인 2개 conv
- 컨볼루션으로 설명하기
 패딩은 언급 없으니 0, 스트라이드는 최소 단위인 1, 입력 크기를 n이라고 하면,
패딩은 언급 없으니 0, 스트라이드는 최소 단위인 1, 입력 크기를 n이라고 하면, 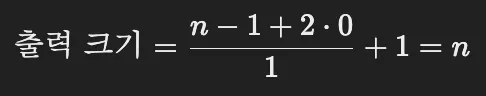
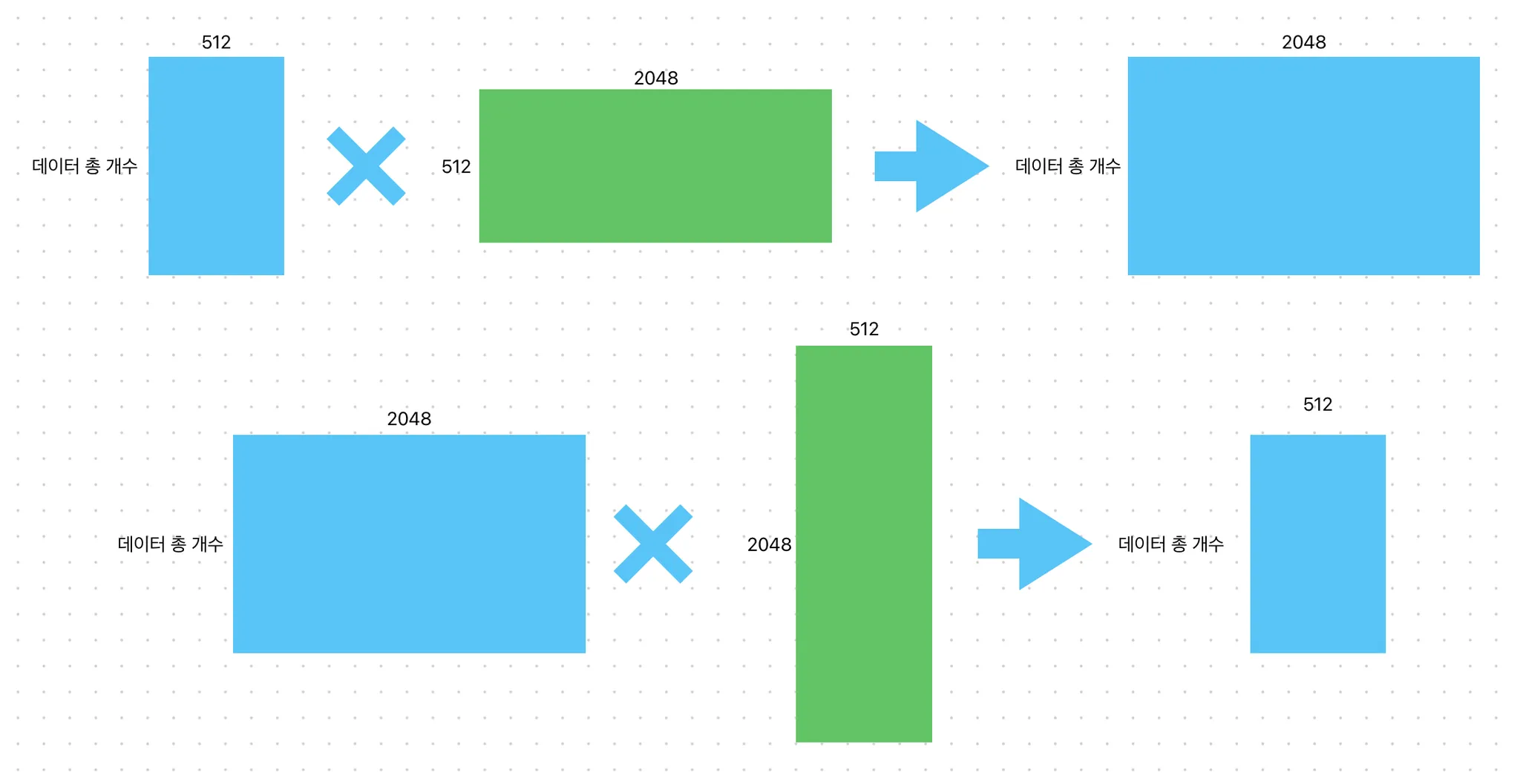
입출력 차원: , FFN 내부 차원
- 위 차원 설명이 부실하다고 생각해서 직접 그려봄. 우선, 임베딩 차원이 512이면, 열 방향으로 512 → 멀티헤드 어텐션 거친 결과 열 방향으로 512 행 방향 차원 크기는 데이터 개수(데이터 하나가 토큰인지 문장인지 헷갈림)

3.4 Embeddings and Softmax
학습된 임베딩: 입출력 토큰을 차원 벡터로 변환
학습된 선형 변환 & 소프트맥스: 디코더 출력을 다음 토큰 확률로 변환
두 임베딩 층(인코더, 디코더)에서 같은 가중치 행렬 공유
선형 변환도 마찬가지
임베딩 층에서 가중치에 곱함
- 뇌피셜* 임베딩하면 일반적으로 값이 작아지니, 키우기 위해서 곱하지 않았을까? 혹시 명확한 설명을 찾은 사람?
3.5 Positional Encoding
recurrence, convolution 없으므로 상대/절대적 위치 정보를 주입해야 함 → 임베딩에 positional encoding 더 해서 인코더/디코더로 들어감
positional encoding이 와 차원이 같아서 덧셈 가능
- 레퍼런스 논문에서 position embedding 부분 발췌 → 레퍼런스 논문에는 그냥 더하는 것만 나옴 포지션 임베딩을 피드백 먹여서 위치 정보를 넣으니 성능이 좋았다 재밌는 점은 출력에 포지션 임베딩 두고 입력에 포지션 임베딩 빼면 정신 못차렸다 → 연구진은 모델이 입력 위치 정보 없이 출력 위치 정보를 잘 찾지 못 한다고 표현함 https://www.geeksforgeeks.org/positional-encoding-in-transformers/ 여기 설명 믿을 수 있나?? 아래 설명은 여기서 나옴 positional encoding을 곱하지 않는 이유: 값의 범위가 크게 변화함 → 학습 불안정, 원래 의미나 위치 정보 왜곡 가능
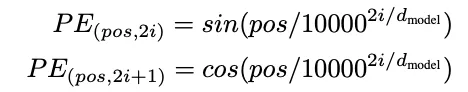
pos는 위치, i는 차원 → 각 positional encoding의 차원은 sinusoid와 대응
상대 위치에 따라 모델이 attend 행위를 학습할 수 있다고 가정 → 괴상한 식..
- 뇌피셜* https://www.geeksforgeeks.org/positional-encoding-in-transformers/ 요기 내용 참고함 주파수의 정의: 에서 를 주파수라고 한다. (로 묶는 경우 각주파수. 여기서는 각주파수랑 주파수를 구분 X) 고주파: 사인/코사인 안에 값(주파수, 진동수의 정의)이 커지는 경우 → i가 작아지는 경우 → 임베딩에서 왼쪽으로 가는 경우(앞 열) 저주파: 사인/코사인 안에 값(주파수, 진동수의 정의)이 작아지는 경우 → i가 커지는 경우 → 임베딩에서 오른쪽으로 가는 경우(뒷 열)
-
인덱스가 0부터 시작해서 짝홀 순서입니다
고주파 - 짝 고주파 - 홀 저주파 - 짝 저주파 - 홀 값이 자주 바뀜(증-감-증-감) 값이 자주 바뀜(감-증-감-증) 값이 덜 바뀜(증-감-증-감) 값이 덜 바뀜(감-증-감-증) 주파수 변화가 지수적으로 이루어진다 → 비대칭 → 같은 토큰이라도 위치가 다르면 비대칭하게 positional encoding을 준다. → 긴 문맥 정보도 학습할 수 있다
-
함수를 고정해서 학습 중에 보지 못한 위치도 표현 가능
k를 오프셋으로 두어서 위치를 선형 변환함 → sin, cos 합차 공식
4. Why Self-Attention
비교를 위한 3개의 기준
-
연산 복잡도 per 층
-
최소 순차 연산량로 측정되는 병렬화 가능한 계산량 → 순차적인 데이터는 병렬화가 안 됨
-
네트워크에서 장거리 의존성 간 경로 길이: 최대 경로 길이
시퀀스 앞뒤로 왔다갔다하는게 학습에 영향을 미침 → 짧으면 쉬움
다양한 레이어로 구성된 네트워크에서 경로 길이도 비교 → 셀프 어텐션, CNN, RNN 비교

연산 복잡도 per 층: 이면 Recurrent보다 셀프 어텐션이 더 빠름
순차 연산량: Recurrent는 인데 셀프 어텐션은 상수
제한된 셀프 어텐션 설명: 출력 위치 중심으로 입력 시퀀스 일부만 참조(윈도우 길이 r) → 최대 경로 길이 복잡도는 로 증가
Convolution에서 이면 입출력 위치 연결 X. Recurrent보다 배 연산 복잡함
- 어텐션 시각화
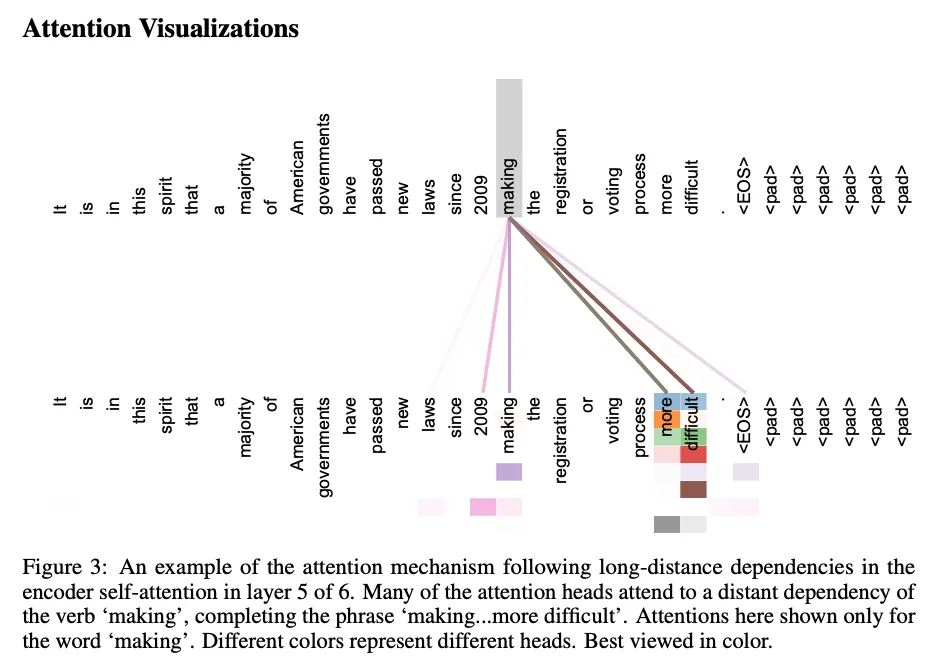
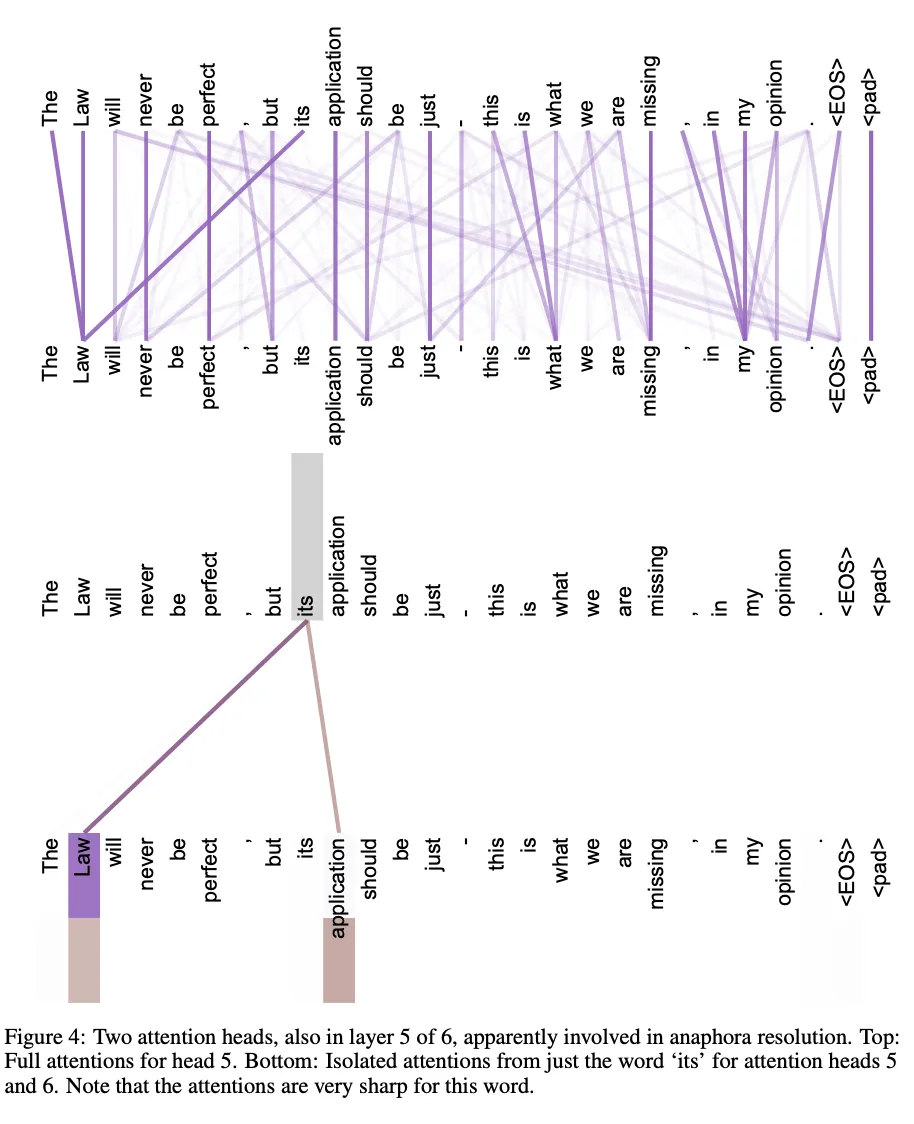
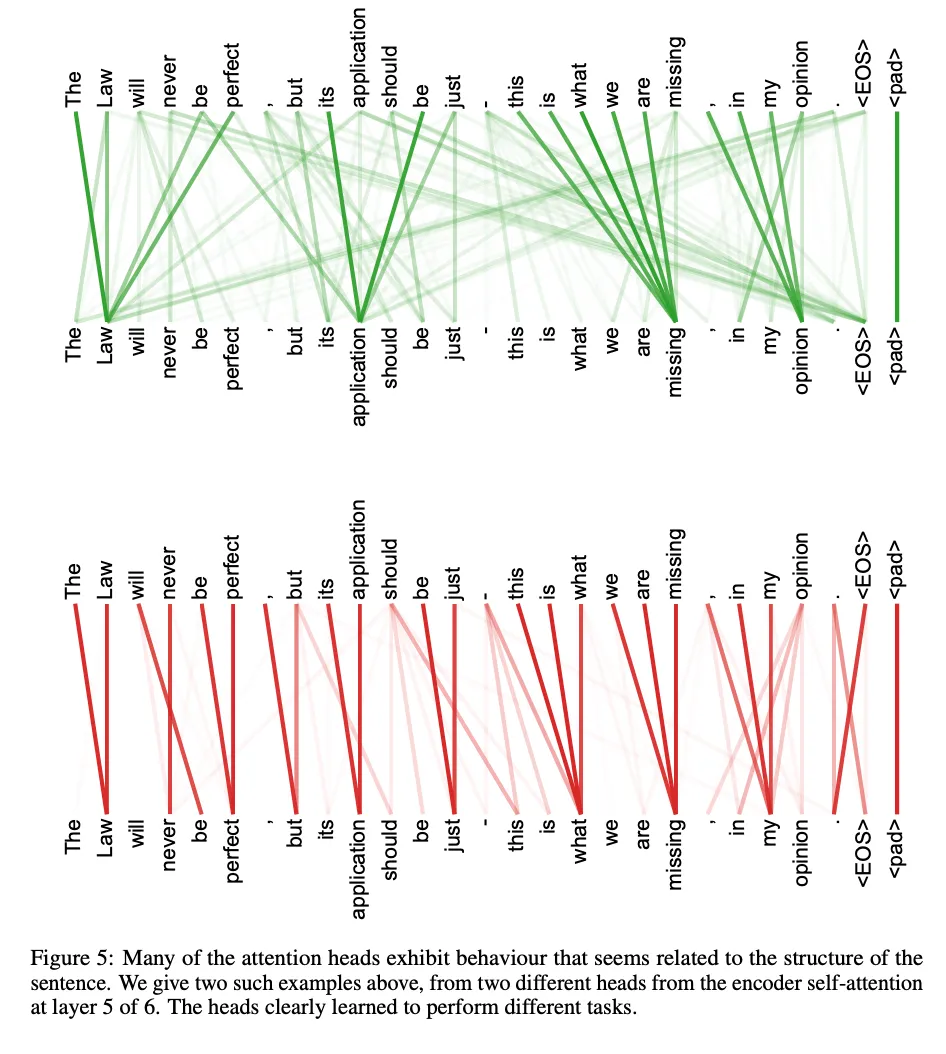
5. Training
5.1 Training Data and Batching
- standard WMT 2014 영-독 데이터: 문장 쌍 450만 개
- 문장 BPE 사용: source-target 어휘 37000 토큰
- larger WMT 2024 영-프 데이터: 문장 쌍 3600만 개
- Word-piece로 32000 토큰
- 문장 쌍은 시퀀스 길이에 따라 배치로 묶음 → 긴 문장 쌍은 긴 문장 쌍끼리, 짧은 문장 쌍은 짧은 문장 쌍끼리
- 각 훈련 배치에는 25000개 소스/타겟 토큰이 포함된 문장 쌍
5.2 Hardware and Schedule
- P100 8개
- 하이퍼파라미터는 과 같이 논문에 명시됨
- 각 훈련 스텝은 0.4초
- 베이스 모델 훈련은 10만 스텝을 12시간 동안 훈련
- 큰 모델은 30만 스텝을 3.5일 동안 훈련
5.3 Optimizer
- 로 세팅한 아담 사용
- learning rate를 학습 중간에 공식에 따라 동적으로 바꿈
- 처음 까지는 학습률을 증가하고 이후에는 천천히 감소함(step의 역제곱근에 비례함) → 미세 조정 가능. 으로 세팅
5.4 Regularization
Residual Drop
- 각 sub-layer의 입력과 normalize에서 드롭아웃 적용
- 인코더/디코더 둘 다 임베딩, positional encoding에도 적용
- 로 설정
Label Smoothing
- 로 설정
- PPL은 안 좋아지는데, 정확도와 BLEU 향상
- Label Smoothing 공식 예시) 원래 원-핫 벡터가 [0, 1, 0, 0, 0]이라 가정 인 경우 → [0.02, 0.88, 0.02, 0.02, 0.02] 이점 1. 과적합 방지되어 일반화 성능 오름 이점 2. 확률 분포가 극단적이지 않고, 안정적이고 균형 있게 학습됨
6. Results
6.1 Machine Translation

WMT 2014 영-독 번역에서 big 모델이 BLEU 28.4 달성
- big 모델은 Table 3 맨 마지막 줄, 학습에는 8개 P100로 3.5일 소요
- 기본 모델은 이전 모델/앙상블을 능가하고, 학습 비용 훨씬 적음
WMT 2014 영-프 번역에서 big 모델이 BLEU 41.0 달성
- big 모델이 모든 단일 모델 능가, 이전 SOTA 모델의 학습 비용 1/4도 안 됨
- 영-프 작업에서는 드랍아웃 비율을 0.3에서 0.1로 설정
- 기본 모델은 10분 간격으로 저장된 마지막 5개 체크포인트를 평균 내어 하나의 모델로 사용함
- big 모델은 마지막 20개 체크포인트 평균 냄
빔 서치 사용함 → 길이는 4, 패널티는
- 빔 서치 그리디 서치와 비슷함: 현재 가장 높은 확률을 우선 고름 그리디 서치와 완전 탐색 사이라고 생각하면 좋을 듯 하지만 유지할 후보 개수를 정함: 위 경우에는 4개. 즉 현재 ~ 4개 이전 토큰을 바탕으로 가장 높은 확률을 우선 고름 시퀀스 확률을 기준으로 평가
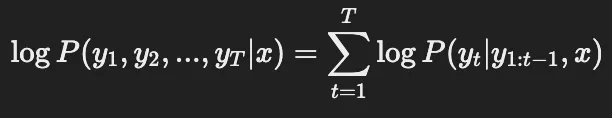 출력 시퀀스가 너무 짧아지는 문제를 해결하기 위해서 패널티를 추가함
출력 시퀀스가 너무 짧아지는 문제를 해결하기 위해서 패널티를 추가함 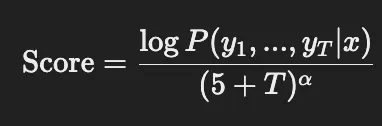
dev set(newstest2013 데이터셋) 실험 후에 선택됨
추론 중 출력 길이 제한을 입력 길이 +50으로 설정. 가능하면 일찍 종료함
부동 소수점 연산 수 추정함: 학습 시간 x GPU 수 x 각 GPU에서 부동 소수점 정밀도(single-precision floating point capacity)
6.2 Model Variation
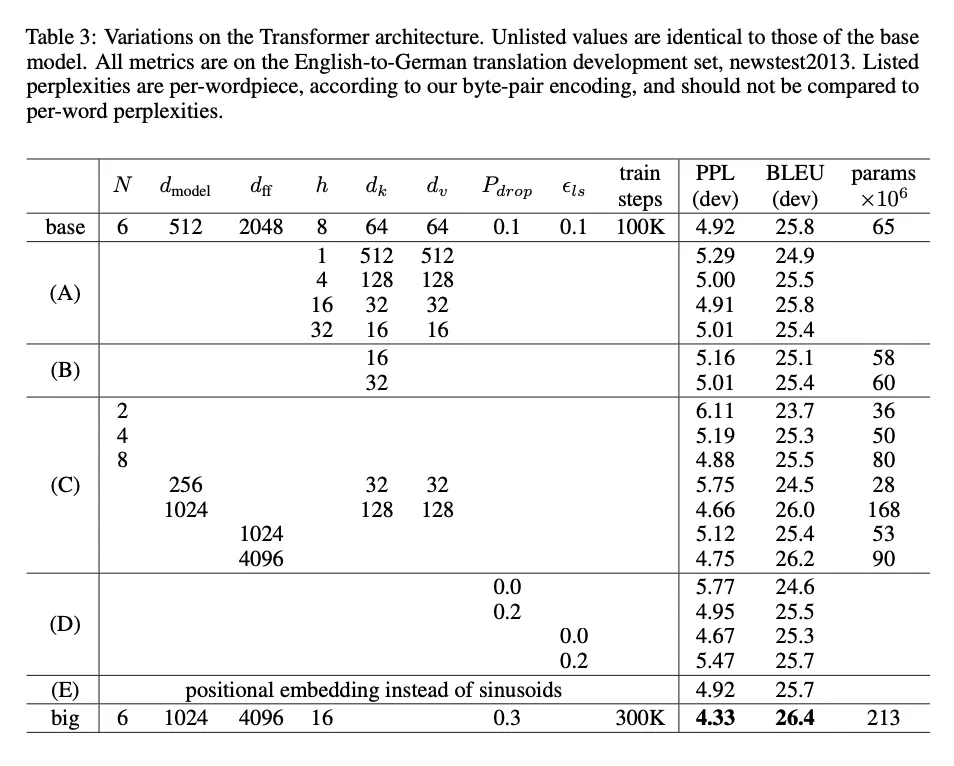
각 구성 요소의 중요성 평가 → 기존 모델 변형. newstest2013 영-독 번역 성능 변화 측정
빔 서치는 썼는데, 체크포인트 평균화는 X
Table 3 (A): 어텐션 헤드 수와 키/값의 차원 변화
- 단일 어텐션은 최적치보다 0.9 BLEU 낮음 → 아마 다양한 관계 학습 안 되서?
- 헤드가 너무 많아도 품질 저하됨 → 계산 복잡도가 증가해서?
Table 3 (B): 어텐션 키 크기 줄여도 모델 품질 저하됨 → 키-쿼리의 유사성 계산에 표현이 부족해지지 않을까? → 더 정교한 함수가 있지 않을까?
Table 3 (C), (D): big 모델이 짱짱, 드롭아웃이 과적합에 좋음
Table 3 (E): positional encoding을 학습 임베딩으로 교체해도 비슷
6.3 English Constituency Parsing
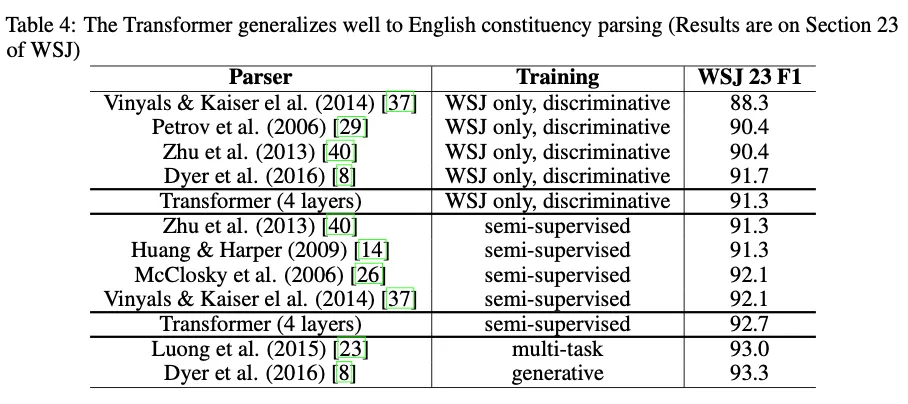
트랜스포머 범용성 평가하기 위해 영어 구성 구문 분석 실험 수행
- 영어 구성 구문 분석 실험: 문장을 트리로 분석함 → 명사구, 동사구를 추출하는 작업
주어진 문장: The quick brown fox jumps over the lazy dog. S ├── NP (The quick brown fox) └── VP (jumps over the lazy dog)
출력이 트리 형식으로 빡세고, 입력보다 길다.
RNN S2S는 작은 데이터셋 환경에서 SOTA 못 했음
4개 층, 설정으로 Penn Treebank에서 추출한 약 4만 개 WSJ 데이터로 학습
정확도 높은 BerkeleyParser corpora 1700만개 문장과 반지도학습 세팅 포함
- BerkeleyParser
WSJ만 사용 → 16000개 어휘, 반지도학습 설정 32000개 어휘 사용
어텐션과 residual하게 적용한 드롭아웃, 학습률, 빔 서치 사이즈만 실험하고 나머지는 영-독 기본 모델 설정 그대로
출력 제한을 입력 길이 + 300으로 늘림
빔 크기 21, 패널티 0.3으로 둠
별도로 작업에 특화해서 튜닝 안해도 RNN 이김. 심지어 WSJ 데이터만 사용해도 BerkeleyParser 이김 ㅎㅎ
7. Conclusion
오직 attention만 사용하는 transduction model인 트랜스포머 제시했음. RNN 안쓰고 멀티헤드어텐션 씀
번역 작업에서 트랜스포머 학습 속도가 RNN/CNN 기반 모델보다 현저히 빠름 → WMT 2014 영-독, 영-프 작업 모두 우리가 SOTA 찍었음. 영-독은 심지어 앙상블도 이김 ㅎㅎ
어텐션 기반 모델의 미래 기대하고 있겠음. 다른 테스크에도 적용해보려고 함. 입출력 modality를 확장해서 이미지, 오디오, 비디오와 같은 대규모 입력과 출력을 효율적으로 처리하고 싶음 → 어텐션 메커니즘 더 파 볼 생각. local: 입력에 일부만, restricted한 어텐션 → 영역 제한해서 거기서 만 어텐션
덜 순차적으로 생성하는 것도 목표임 → 병렬화할 수 있음
무슨 문제 때문에(또는 왜) 이 논문을 냈는가
- 이전까지 RNN/CNN 기반 모델들이 시퀀스 관련 작업에서 성능이 가장 좋았음
- 이전까지 쓰이던 어텐션 메커니즘, End-to-End Memory Network도 RNN 기반 RNN/CNN 기반 모델은 기울기 소실/폭발이라는 근본적인 문제를 해결하지 못했음
- 즉, 멀리 떨어져 있는 정보를 학습하지 못했음
그래서 문제를 어떻게 해결했는가
- RNN/CNN을 배제한 모델을 설계함
- attention 매커니즘을 활용함
- self-attention으로 각 위치에서 전체 문맥을 학습하도록 설계
결과는 어땠는가
- WMT 2014 영-독/영-프 번역 SOTA
- 영-독은 앙상블해서 28.4 BLEU 달성
- 영-프는 8개 GPU로 3.5일 학습해서 41.8 BLEU 달성 → 학습 시간도 문헌 상 논문 중에 제일 빨랐다고 합니다.
- WSJ로 학습해서 구문 분석 테스크는 BerkeleyParser랑 RNN 이겼다고 합니다.
