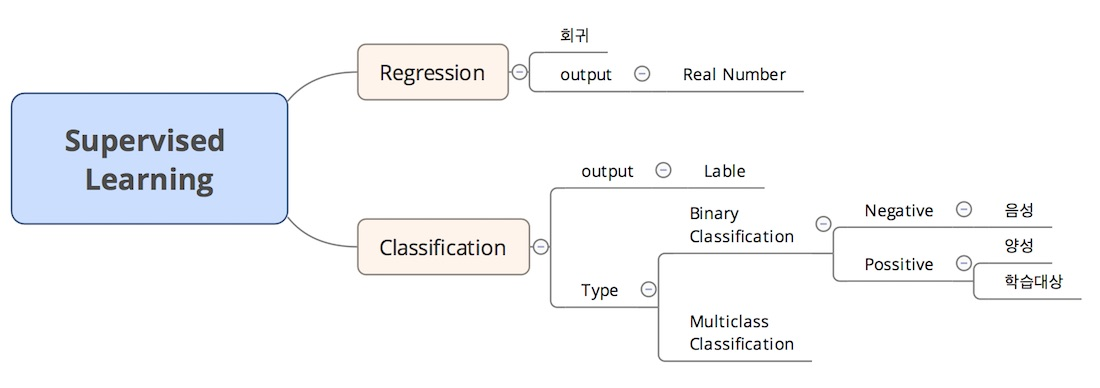
지도학습(Supervised Learning)
- 정답 label을 적절하게 예측하도록 학습하는 머신러닝 방법
- 분류(Classification)와 회귀(Regression)
특성 공학(Feature Engineering)
- GIGO(Garbage In, Garbage Out)
- 데이터나 변수들을 중복되지 않고, 현실문제에 맞도록 재분류함
- 변형해 새로운 Feature로 내보내는 것
[1] 분류
→ 범주형(Categorical) 데이터
□ 데이터 형태에 따른 분류
1. 이미지 내의 대상
- CNN 활용(딥러닝)
- 이미지 특징 추출
2. 콘텐츠 내용에 따라 주제 분류
- 텍스트마이닝: 텍스트의 단어를 토큰화하여 사용된 언어에 따라 글의 주제 분류
- 언어모델: 문장이나 문단 단위로 쓰인 텍스트 정보를 임베딩(단어 의미 공간에 벡터화)하여 주제 분류
3. 정형 데이터 분류
- df을 입력받아 분류
- 각 열이 하나의 특성이 되고, 이를 바탕으로 분류
□ 예측하는 범주의 개수에 따른 분류
1. 이진 분류 (Binary Classification)
- 참/거짓으로 나눌 수 있음
- 임계치가 0.5이지만 데이터가 불균형한 경우 조정 필요
- 예시: 호텔 취소 여부 예측
2. 다중 분류(Mulitple Classification)
- 예측범주가 3개 이상
- 예시: 피파 선수 포지션 할당
[2] 회귀
→ 연속형(continuous) 데이터
- 실제로 정확한 값이 나오도록 가중치 조정 필요
- 정확도는 실제값과 예측값의 차이로 판단
- 예시: 집값 예측
지도학습 머신러닝 모델
(1) KNN(K-nearest neighbors)
- K-초근접 이웃, 분류문제 알고리즘으로 활용
- 특정 포인트와 가까운 순으로 K개의 이웃 데이터를 선정!
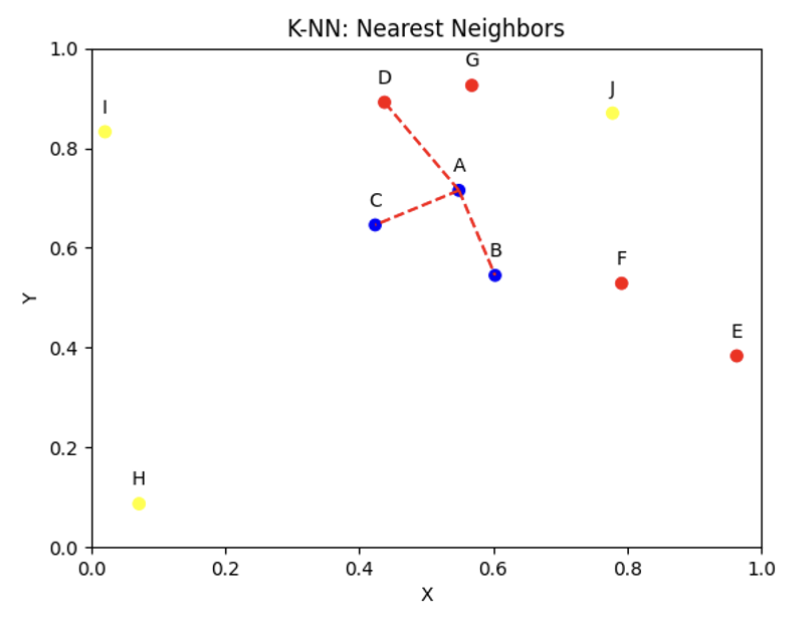
▶ KNN 설명 및 코드
1. 거리 계산
- 분류하려는 입력 데이터와 훈련 데이터 간의 거리를 계산
- 일반적으로 유클리디안 거리(Euclidean distance)가 사용
def _euclidean_distance(self, x1, x2):
return np.sqrt(np.sum((x1 - x2)**2))
def _predict(self, x):
# x와 훈련 세트의 모든 예제 사이의 거리 계산
distances = [self._euclidean_distance(x, x_train) for x_train in self.X_train]
2. 가까운 이웃 선택
- 입력 데이터와 가장 가까운 K개의 이웃을 선택 (하이퍼파라미터)
- K는 일반적으로 홀수로 설정 -> 이후 다수결 투표를 진행예정이기 때문
def _predict(self, x):
...
# 거리를 기준으로 정렬하고 첫 k개 이웃의 인덱스 반환
k_indices = np.argsort(distances)[:self.k]
# k개의 가장 가까운 이웃 훈련 샘플의 레이블 추출
k_nearest_labels = [self.y_train[i] for i in k_indices]3. 다수결 투표
- 선택된 K개의 이웃들의 정답 레이블을 확인
- 다수결 투표를 통해 입력 데이터의 레이블을 결정
- 가장 많은 표를 얻은 레이블이 입력 데이터의 예측 레이블이 됨
def _predict(self, x):
...
# 다수결 투표 이후 클래스 레이블 반환
most_common = np.argmax(np.bincount(k_nearest_labels))
return most_common▶ KNN 전체 코드
import numpy as np
class KNN:
def __init__(self, k=3):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
y_pred = [self._predict(x) for x in X]
return np.array(y_pred)
def _euclidean_distance(self, x1, x2):
return np.sqrt(np.sum((x1 - x2)**2))
def _predict(self, x):
# x와 훈련 세트의 모든 예제 사이의 거리 계산
distances = [self._euclidean_distance(x, x_train) for x_train in self.X_train]
# 거리를 기준으로 정렬하고 첫 k개 이웃의 인덱스 반환
k_indices = np.argsort(distances)[:self.k]
# k개의 가장 가까운 이웃 훈련 샘플의 레이블 추출
k_nearest_labels = [self.y_train[i] for i in k_indices]
# 다수결 투표 이후 레이블 반환
most_common = np.argmax(np.bincount(k_nearest_labels))
return most_common(2) SVM (Support Vector Machine)
- 분류나 회귀 분석하는데 사용
- SVM은 가장 잘 분류할 수 있는 최적 결정 경계를 찾음
- 2차원에서는 직선으로, 3차원 이상에서는 초평면(Hyperplane)으로 결정 경계 찾음
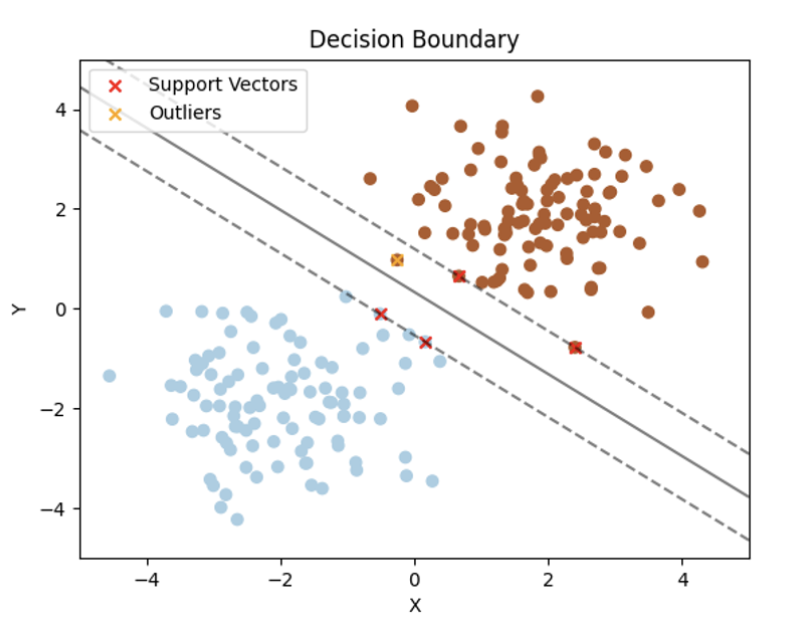
▶ SVM 설명 및 코드
1. 데이터 분류를 위한 최적의 결정 경계 찾기
- 데이터들을 고차원공간으로 매핑한 뒤, 해당 공간에서 데이터를 최적으로 분리할 수 있는 초평면을 찾음
- 초평면은 클래스 간의 거리를 최대화하는 방식으로 결정
2. 서포트 벡터
- 서포트 벡터: 데이터와 초평면 사이의 경계 영역에 위치한 데이터 포인트들 (그림에서 붉은색 X 된 데이터 포인트)
3. 마진 최대화
- margin: 결정경계와 서포트 벡터간의 거리
- margin 커질수록, 일반화 능력 향상
class SVM:
def fit(self, X, y):
...
# 경사 하강법 최적화로 마진 최대화
for _ in range(self.num_iterations):
for i in range(n_samples):
if y[i] * (np.dot(X[i], self.w) - self.b) >= 1:
self.w -= self.learning_rate * (2 * self.lambda_param * self.w)
else:
self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(X[i], y[i]))
self.b -= self.learning_rate * y[i]▶ SVM 전체 코드
# SVM 클래스 정의
class SVM:
def __init__(self, learning_rate=0.01, lambda_param=0.01, num_iterations=1000):
self.learning_rate = learning_rate
self.lambda_param = lambda_param
self.num_iterations = num_iterations
self.w = None
self.b = None
# fit 함수 정의
def fit(self, X, y):
# y<=0을 만족하면 -1, 만족하지 않으면 1을 출력
y = np.where(y <= 0, -1, 1)
n_samples, n_features = X.shape
# 가중치 초기화
self.w = np.zeros(n_features)
self.b = 0
# 경사 하강법 최적화
for _ in range(self.num_iterations):
for i in range(n_samples):
if y[i] * (np.dot(X[i], self.w) - self.b) >= 1:
self.w -= self.learning_rate * (2 * self.lambda_param * self.w)
else:
self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(X[i], y[i]))
self.b -= self.learning_rate * y[i]
def predict(self, X):
linear_output = np.dot(X, self.w) - self.b
return np.sign(linear_output)
# 0보다 작으면 -1, 0보다 크면 1로 반환
(3) 로지스틱 회귀 (Logistic Regression)
- 이진 분류 문제에 많이 활용됨
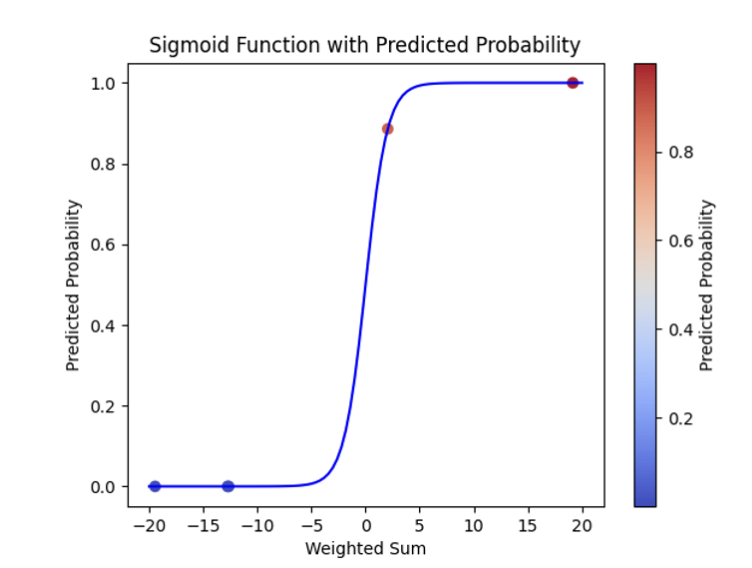
▶ LR 설명 및 코드
1. 입력 데이터와 가중치 행렬 선형 조합
- z는 입력 특성들과 가중치의 선형 조합을 나타냄
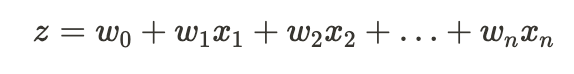
2. 로지스틱함수에 z입력
- 활성화함수인 시그모이드(Sigmoid)함수를 이용
- 시그모이드 함수는 눕힌 S자 모형의 출력을 0과 1사이로 제한
- 는 양성 클래스의 확률을 나타냄
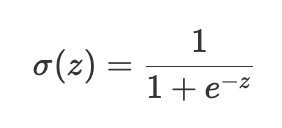
3. 경사하강법
- 로지스틱 손실이라고 불리는 비용함수를 최소화하는 최적의 가중치를 학습
- 비용함수는 예측된 확률과 실제 클래스 레이블 간의 유사성을 측정
- 경사하강법과 같은 최적화 기법을 사용하여 반복적으로 조정 및 최적의 파라미터 찾음
- 로지스틱 회귀는 일반적으로 0.5로 설정된 결정 경계 임계값 사용
- 임계값 초과시 양성클래스로 분류
class LogisticRegression:
...
def fit(self, X, y):
num_samples, num_features = X.shape
# 가중치 및 편향 초기화
self.weights = np.zeros(num_features)
self.bias = 0
# 경사 하강법 최적화
for _ in range(self.num_iterations):
linear_model = np.dot(X, self.weights) + self.bias
predicted_labels = self.sigmoid(linear_model)
# 기울기 계산
dw = (1 / num_samples) * np.dot(X.T, (predicted_labels - y))
db = (1 / num_samples) * np.sum(predicted_labels - y)
# 파라미터 업데이트
self.weights -= self.learning_rate * dw
self.bias -= self.learning_rate * db
▶ LR 전체 코드
import numpy as np
# 로지스틱 회귀 class 정의
class LogisticRegression:
def __init__(self, learning_rate=0.01, num_iterations=1000):
self.learning_rate = learning_rate
self.num_iterations = num_iterations
self.weights = None
self.bias = None
# 활성화 함수인 시그모이드 함수 정의
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
# fit 함수 정의
def fit(self, X, y):
num_samples, num_features = X.shape
# 가중치 및 편향 초기화
self.weights = np.zeros(num_features)
self.bias = 0
# 경사 하강법 최적화
for _ in range(self.num_iterations):
linear_model = np.dot(X, self.weights) + self.bias
predicted_labels = self.sigmoid(linear_model)
# 기울기 계산
dw = (1 / num_samples) * np.dot(X.T, (predicted_labels - y))
db = (1 / num_samples) * np.sum(predicted_labels - y)
# 파라미터 업데이트
self.weights -= self.learning_rate * dw
self.bias -= self.learning_rate * db
# 예측함수 정의
def predict(self, X):
linear_model = np.dot(X, self.weights) + self.bias
predicted_labels = self.sigmoid(linear_model)
predicted_labels = np.where(predicted_labels >= 0.5, 1, 0)
return predicted_labels
(4) 의사 결정 나무 (DT)
- 의사결정나무(Decision Tree)는 분류와 회귀 문제에 널리 사용
- 데이터를 분할하여 특성에 따라 의사결정 규칙을 학습하고, 이를 통해 새로운 데이터 포인트를 예측
- 장점: DT는 해석이 용이, 특성의 중요도를 파악 가능
- 단점: 데이터의 비선형 관계를 잘 처리하지 못하는 단점 존재
- 극복: 앙상블 기법인 RF등을 활용해 모델의 성능 향상 가능
▶ DT 설명 및 코드
1. 엔트로피 계산
-
데이터의 불확실성을 나타내는 척도

-
엔트로피⬆ 혼잡도⬆ 불순도⬆ | 5:5면 불순도가 높다!!
- (5:5)로 나뉘었다 => 불순도⬆
- (1:9)로 나뉘었다 => 불순도⬇
import numpy as np
class DecisionTree:
def __init__(self, max_depth=None):
self.max_depth = max_depth
self.tree = {}
def entropy(self, y):
_, counts = np.unique(y, return_counts=True)
probabilities = counts / len(y)
entropy = -np.sum(probabilities * np.log2(probabilities))
return entropy
2. 정보 이득 최대화
- DT는 엔트로피를 사용하여 데이터를 분할할 때 정보 이득(Gain) 최대화⬆ 방향으로 학습(분할 유용 방향)
- Gain⬆ = 분할 전 후의 엔트로피 차이
class DecisionTree:
...
def information_gain(self, X, y, feature_idx, threshold):
left_mask = X[:, feature_idx] <= threshold
right_mask = X[:, feature_idx] > threshold
left_y = y[left_mask]
right_y = y[right_mask]
left_entropy = self.entropy(left_y)
right_entropy = self.entropy(right_y)
left_weight = len(left_y) / len(y)
right_weight = len(right_y) / len(y)
# GAIN: 분할된 하위 노드의 엔트로피들의 가중평균을 뺀 값
information_gain = self.entropy(y) - (left_weight * left_entropy + right_weight * right_entropy)
return information_gain
3. 최적의 임계값(Thresholds) 찾기
- Gain을 기준으로 데이터를 분할할 최적의 특성과 임계값을 찾음
def split(self, X, y):
num_samples, num_features = X.shape
best_info_gain = 0
best_feature_idx = None
best_threshold = None
for feature_idx in range(num_features):
thresholds = np.unique(X[:, feature_idx])
# 입력 데이터 특성이 임계값 후보
for threshold in thresholds:
# 정보 획득량 계산
info_gain = self.information_gain(X, y, feature_idx, threshold)
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature_idx = feature_idx
best_threshold = threshold
left_mask = X[:, best_feature_idx] <= best_threshold
right_mask = X[:, best_feature_idx] > best_threshold
left_X = X[left_mask]
left_y = y[left_mask]
right_X = X[right_mask]
right_y = y[right_mask]
return best_feature_idx, best_threshold, left_X, left_y, right_X, right_y
4. 의사결정나무 구축
- 데이터를 분할하고, 정지 기준을 충족할때까지 의사결정나무를 계속 구축
- 정지기준: 최대깊이 or 순수한 리프 노드
def build_tree(self, X, y, depth=0):
num_samples, num_features = X.shape
# 기저 사례(base case): 최대 깊이에 도달하거나 순수한 리프 노드(pure leaf nodes)인 경우
if len(np.unique(y)) == 1 or depth == self.max_depth:
_, counts = np.unique(y, return_counts=True)
leaf_label = np.argmax(counts)
return leaf_label
feature_idx, threshold, left_X, left_y, right_X, right_y = self.split(X, y)
decision_node = {
'feature_idx': feature_idx,
'threshold': threshold,
'left': self.build_tree(left_X, left_y, depth+1),
'right': self.build_tree(right_X, right_y, depth+1)
}
return decision_node
▶ DT 전체 코드
# DT 클래스 정의, max_depth 등
class DecisionTree:
def __init__(self, max_depth=None):
self.max_depth = max_depth
self.tree = {}
# 엔트로피 정의
def entropy(self, y):
_, counts = np.unique(y, return_counts=True)
probabilities = counts / len(y)
entropy = -np.sum(probabilities * np.log2(probabilities))
return entropy
# Gain 정의 및 최대화 방향
def information_gain(self, X, y, feature_idx, threshold):
left_mask = X[:, feature_idx] <= threshold
right_mask = X[:, feature_idx] > threshold
left_y = y[left_mask]
right_y = y[right_mask]
left_entropy = self.entropy(left_y)
right_entropy = self.entropy(right_y)
left_weight = len(left_y) / len(y)
right_weight = len(right_y) / len(y)
information_gain = self.entropy(y) - (left_weight * left_entropy + right_weight * right_entropy)
return information_gain
# 최적의 임계값(Thresholds) 찾기
def split(self, X, y):
num_samples, num_features = X.shape
best_info_gain = 0
best_feature_idx = None
best_threshold = None
for feature_idx in range(num_features):
thresholds = np.unique(X[:, feature_idx])
# 입력 데이터 특성이 임계값 후보
for threshold in thresholds:
# 정보 획득량 계산
info_gain = self.information_gain(X, y, feature_idx, threshold)
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature_idx = feature_idx
best_threshold = threshold
left_mask = X[:, best_feature_idx] <= best_threshold
right_mask = X[:, best_feature_idx] > best_threshold
left_X = X[left_mask]
left_y = y[left_mask]
right_X = X[right_mask]
right_y = y[right_mask]
return best_feature_idx, best_threshold, left_X, left_y, right_X, right_y
# 의사결정나무 구축
def build_tree(self, X, y, depth=0):
num_samples, num_features = X.shape
# 최대깊이에 도달하거나 순수한 리프 노드인 경우 : 기저 사례
if len(np.unique(y)) == 1 or depth == self.max_depth:
_, counts = np.unique(y, return_counts=True)
leaf_label = np.argmax(counts)
return leaf_label
feature_idx, threshold, left_X, left_y, right_X, right_y = self.split(X, y)
decision_node = {
'feature_idx': feature_idx,
'threshold': threshold,
'left': self.build_tree(left_X, left_y, depth + 1),
'right': self.build_tree(right_X, right_y, depth + 1)
}
return decision_node
def fit(self, X, y):
self.tree = self.build_tree(X, y)
def predict_sample(self, x, tree):
if isinstance(tree, int):
return tree
feature_idx = tree.get('feature_idx')
threshold = tree.get('threshold')
if x[feature_idx] <= threshold:
if isinstance(tree['left'], dict):
return self.predict_sample(x, tree['left'])
else:
return tree['left']
else:
if isinstance(tree['right'], dict):
return self.predict_sample(x, tree['right'])
else:
return tree['right']
def predict(self, X):
predictions = []
for x in X:
prediction = self.predict_sample(x, self.tree)
predictions.append(prediction)
return np.array(predictions)
[출처 | 딥다이브 Code.zip 매거진]
