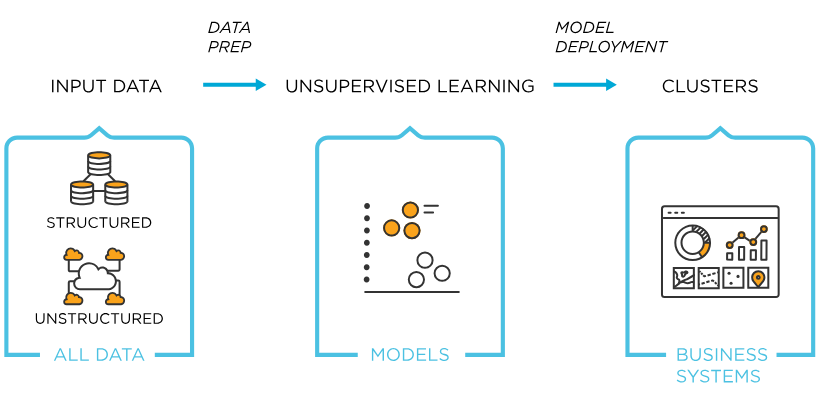
비지도학습(Unsupervised Learning)
- 정답 데이터가 없는 경우에도 활용 가능한 학습방법
- 데이터의 특성 및 구조를 바탕으로 보다 객관적인 의견 제시 가능
- 크게 군집화, 차원축소로 구성
[1] K-Means Clustering
- 데이터 포인트과 중심점 사이의 거리를 기반으로 각 군집의 기준을 설정
- K는 군집의 개수, Means는 군집에 선택된 데이터 포인트들의 평균(중심점)
▶ 1단계: 군집의 개수 설정
- 초기 개수 설정에 따라 결과가 많이 달라짐
- 정답 레이블이 없어서, 최적의 군집을 알기 어려움
- 여러번 실험을 반복해 최적의 군집을 찾거나, 군집 평가 지표를 활용 가능
class KMeans:
def __init__(self, n_clusters, max_iters=100):
self.n_clusters = n_clusters # 군집의 개수 K 지정
self.max_iters = max_iters # 최대 학습 반복횟수 지정
self.centroids = None # 중심점 변수를 설정▶ 2단계: K개의 초기 중심점(Centroid, 무게중심) 설정
- K개의 초기 중심점(Centroid, 무게중심)을 설정
- Scikit-Learn에서 내장되어 있는 K-Means ++ 알고리즘에 따라 초기 중심점 지정
def fit(self, X):
n_samples, n_features = X.shape
# 무작위로 중심점 초기화 - 클러스터 개수를 초기 중심점으로 설정
random_indices = np.random.choice(n_samples, self.n_clusters, replace=False)
self.centroids = X[random_indices]▶ 3단계: 모든 데이터를 가장 가까운 중심점으로 할당 (군집 할당)
- 유클리디안 거리를 계산
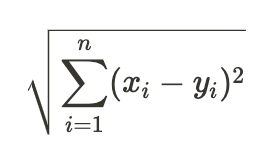
def _euclidean_distances(self, X, Y):
distances = np.sqrt(np.sum((X[:, np.newaxis] - Y)**2, axis=2))
return distancesdef _assign_labels(self, X):
distances = self._euclidean_distances(X, self.centroids)
labels = np.argmin(distances, axis=1)
return labels ▶ 4단계: 군집 내 데이터들의 평균점을 새로운 중심점으로 갱신
def _update_centroids(self, X, labels):
new_centroids = np.zeros_like(self.centroids)
for cluster in range(self.n_clusters):
# 특정 클러스터에 해당하는 포인트 모음
cluster_points = X[labels == cluster]
# 특정 클러스터 포인트의 중심점을 찾기 위해 평균을 계산
new_centroid = np.mean(cluster_points, axis=0)
# 새로운 클러스터로 할당
new_centroids[cluster] = new_centroid
return new_centroids
▶ 5단계: 더이상 중심점이 갱신되지 않을때까지 3-4번 반복
- 장점: 직관적으로 이해 가능, 처리 속도 빨라 많은 데이터 다루기 가능
- 단점: 모든 특성들이 연속적이여야 가능, 군집의 밀도나 크기가 다른 경우 군집화 어려움
def fit(self, X):
...
for _ in range(self.max_iters):
# 각 샘플에 레이블 할당
labels = self._assign_labels(X)
# 중심점 업데이트
new_centroids = self._update_centroids(X, labels)
# 중심점이 수렴했는지 확인
if np.allclose(self.centroids, new_centroids):
break
# 더 이상 업데이트 되지 않으면 훈련을 중단
self.centroids = new_centroids
▶ K-means 전체 코드
import numpy as np
# K-Means 정의
class KMeans:
def __init__(self, n_clusters, max_iters=100):
self.n_clusters = n_clusters
self.max_iters = max_iters
self.centroids = None
# K개의 초기 중심점을 내장되어있는 알고리즘에 따라 지정
def fit(self, X):
n_samples, n_features = X.shape
# 무작위로 중심점 초기화
random_indices = np.random.choice(n_samples, self.n_clusters, replace=False)
self.centroids = X[random_indices]
# 더이상 중심점이 갱신되지 않을때가지 3-4번 방복
for _ in range(self.max_iters):
# 각 샘플에 레이블 할당
labels = self._assign_labels(X)
# 중심점 업데이트
new_centroids = self._update_centroids(X, labels)
# 중심점이 수렴했는지 확인
if np.allclose(self.centroids, new_centroids):
break
# 더이상 업데이트 안되면 훈련 중단
self.centroids = new_centroids
# 유클리디안으로 군집 할당
def _assign_labels(self, X):
distances = self._euclidean_distances(X, self.centroids)
labels = np.argmin(distances, axis=1)
return labels
# 군집 내 데이터들의 평균점을 새로운 중심점으로 갱신
def _update_centroids(self, X, labels):
new_centroids = np.zeros_like(self.centroids)
for cluster in range(self.n_clusters):
# 특정 클러스터에 해당하는 포인트 모음
cluster_points = X[labels == cluster]
# 특정 클러스터 포인트들의 중심점을 찾기위해 평균 계산
new_centroid = np.mean(cluster_points, axis=0)
# new 클러스터로 할당
new_centroids[cluster] = new_centroid
return new_centroids
# 군집 할당을 위한 유클리디안 정의
def _euclidean_distances(self, X, Y):
distances = np.sqrt(np.sum((X[:, np.newaxis] - Y)**2, axis=2))
return distances
def predict(self, X):
labels = self._assign_labels(X)
return labels
[2] DBSCAN
- Density-Based Spatial Clustering of Application with Noise
- 데이터 포인트를 기준으로 지정된 반경 내에 있는 데이터 포인트의 개수에 따라 군집이 형성
- 설정값 -> 반경(Epsilon), 반경 내 최소 데이터 포인트수(minPts)
- 모든 데이터들마다 하나의 코어(원)가 형성
- 코어를 형성하지 못한 데이터포인트는 Border Point와 Noise Point로 구분
◦ Border Point: 최소 데이터 포인트 수를 충족 시키지는 못하지만 반경 내 코어 포인트가 포함되어 있음
◦ Noise Point: 최소 데이터 포인트 수를 충족 시키지는 못하지만 반경 내 코어 포인트가 포함되어 있지 않음
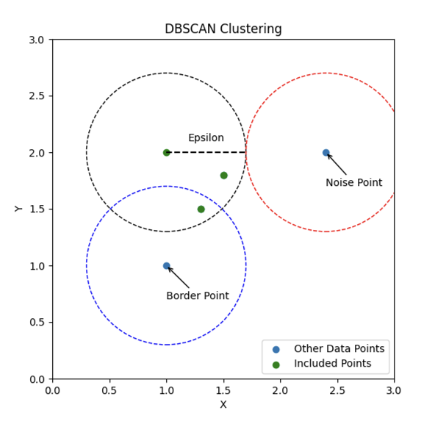
▶ 1단계: 주어진 거리 범위(Epsilon) 내에서 포인트의 이웃들을 찾음
# 주어진 거리내에서 포인트들의 이웃을 찾는 함수 정의
def _get_neighbors(self, X, i):
distances = np.linalg.norm(X - X[i], axis=1)
neighbors = np.where(distances <= self.eps)[0]
return neighbors▶ 2단계: 도달 가능한 포인트를 추가하여 클러스터를 확장해감
# 현재 데이터 포인트를 클러스터에 할당
def _expand_cluster(self, X, i, neighbors, cluster_label, visited):
self.labels[i] = cluster_label
# 새로운 이웃들을 현재 이웃들에 추가
j = 0
while j < len(neighbors):
neighbor = neighbors[j]
if not visited[neighbor]:
visited[neighbor] = True
new_neighbors = self._get_neighbors(X, neighbor)
if len(new_neighbors) >= self.min_samples:
neighbors = np.concatenate((neighbors, new_neighbors))
# 이웃을 현재 클러스터에 할당
if self.labels[neighbor] == 0:
self.labels[neighbor] = cluster_label
j += 1
▶ 3단계: 모든 데이터 샘플에 대해서 클러스터 할당
- DBSCAN은 군집의 수를 지정하지 않아도 군집을 형성할 수 있음
- Noise Point 개념을 도입하여 이상치에 군집이 민감하게 반응하지 않도록 함
# DBSCAN 정의
class DBSCAN:
def __init__(self, eps=0.5, min_samples=5):
self.eps = eps
self.min_samples = min_samples
self.labels = None
def fit(self, X):
n_samples = X.shape[0]
self.labels = np.zeros(n_samples, dtype=int)
visited = np.zeros(n_samples, dtype=bool)
cluster_label = 0
for i in range(n_samples):
if visited[i]: # 이미 방문한 적이 있다(클러스터가 할당되었다)면 continue
continue
visited[i] = True
neighbors = self._get_neighbors(X, i)
if len(neighbors) < self.min_samples:
self.labels[i] = -1 # Noise point
else:
cluster_label += 1
self._expand_cluster(X, i, neighbors, cluster_label, visited)
▶ DBSCAN 전체코드
import numpy as np
# DBSCAN 정의
class DBSCAN:
def __init__(self, eps=0.5, min_samples=5):
self.eps = eps
self.min_samples = min_samples
self.labels = None
def fit(self, X):
n_samples = X.shape[0]
self.labels = np.zeros(n_samples, dtype=int)
visited = np.zeros(n_samples, dtype=bool)
cluster_label = 0
for i in range(n_samples):
if visited[i]: # 클러스터가 할당되었다면 continue
continue
visited[i] = True
neighbors = self._get_neighbors(X, i)
if len(neighbors) < self.min_samples:
self.labels[i] = -1 # Noise point
else:
cluster_label += 1
self._expand_cluster(X, i, neighbors, cluster_label, visited)
# 주어진 거리범위(Epsilon) 내에서 포인트들의 이웃을 찾음
def _get_neighbors(self, X, i):
distances = np.linalg.norm(X - X[i], axis=1)
neighbors = np.where(distances <= self.eps)[0]
return neighbors
# 도달 가능한 포인트를 추가하며 클러스터를 확장해감
def _expand_cluster(self, X, i, neighbors, cluster_label, visited):
self.labels[i] = cluster_label # 현재 데이터 포인트를 클러스터에 할당
j = 0
while j < len(neighbors):
neighbor = neighbors[j]
if not visited[neighbor]:
visited[neighbor] = True
new_neighbors = self._get_neighbors(X, neighbor)
if len(new_neighbors) >= self.min_samples:
neighbors = np.concatenate((neighbors, new_neighbors))
# 새로운 이웃들을 현재 이웃들에 추가
if self.labels[neighbor] == 0:
self.labels[neighbor] = cluster_label
# 이웃을 현재 클러스터에 할당
j += 1
def predict(self, X):
return self.labels
K-Means & DBSCAN 결과 비교
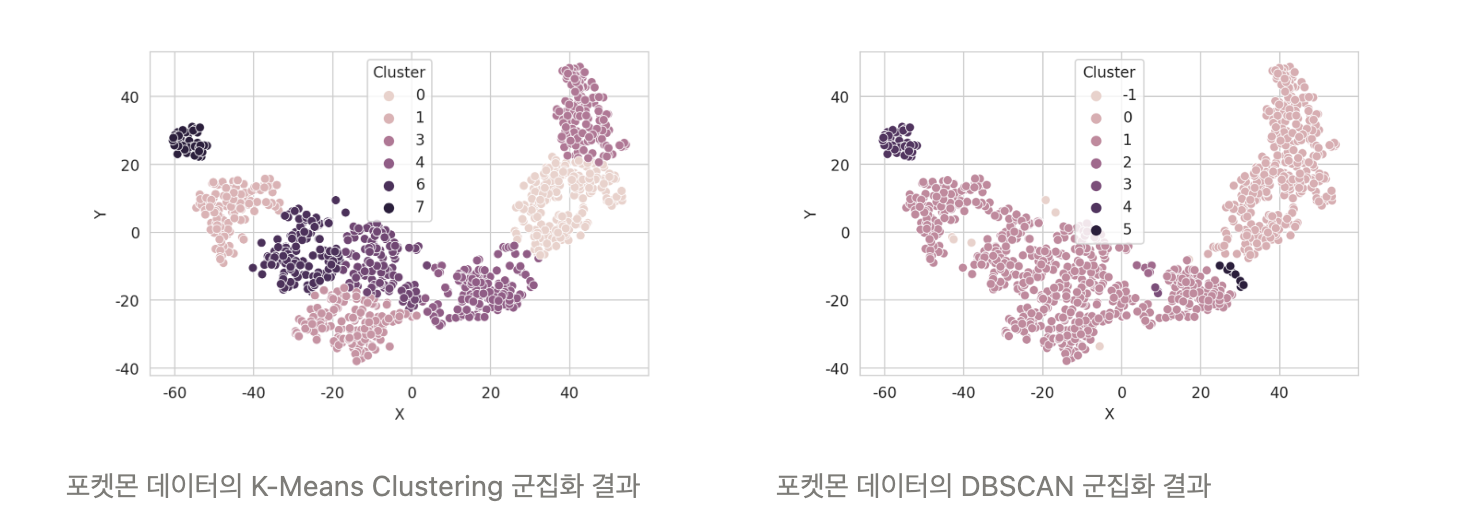
[3] 차원축소방법
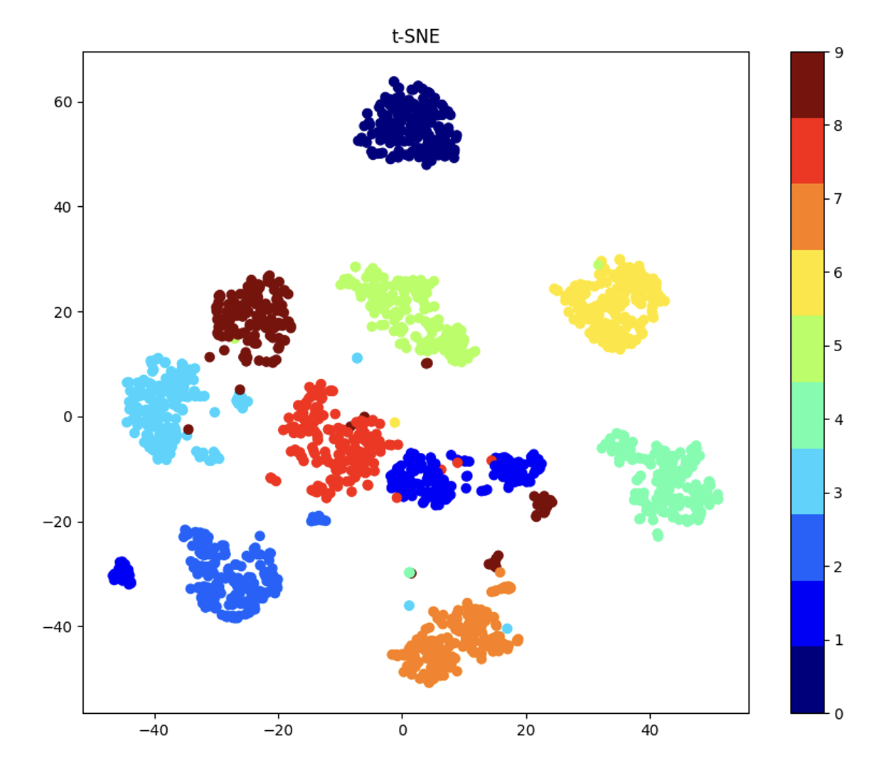
● t-SNE
- 고차원 데이터를 저차원 공간으로 변환한는 비지도 차원축소 알고리즘
- 비슷한 데이터는 비슷한 형태로 근접하게 변환
- 다른 데이터는 멀리 떨어져 변환
- 각 데이터 포인트의 상관관계를 유지하며 데이터 변환 (시각화에 적합)
- 수학적 원리: t-스튜던트 분포, 경사 하강법
▶ 예제 코드
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
digits = load_digits()
X = digits.data
y = digits.target
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
plt.figure(figsize=(10, 8))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap=plt.cm.get_cmap("jet", 10))
plt.colorbar(ticks=range(10))
plt.title("t-SNE")
plt.show()
● PCA 주성분 분석
- Principal Component Analysis
- 분산이 가장 큰(데이터의 분포를 가장 잘 설명하는) 요소를 남긴다
- 데이터의 중요한 특성들을 추출하여 저차원 공간에 투영 (Dimension Reduction)
- 특성추출 Feature Extraction
- 특성공학 Feature Engineering
- 수학적 원리: 공돌이의 수학정리 노트
▶ PCA 전체 코드
import numpy as np
def pca(X, num_components):
# 데이터 중심화
X_centered = X - np.mean(X, axis=0)
# 공분산 행렬 계산
cov_matrix = np.cov(X_centered.T)
# 공분산 행렬의 고윳값과 고유벡터 계산
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 고유값을 내림차순으로 정렬
sorted_indices = np.argsort(eigenvalues)[::-1]
sorted_eigenvalues = eigenvalues[sorted_indices]
sorted_eigenvectors = eigenvectors[:, sorted_indices]
# 상위 k개의 고유벡터 선택 (주성분)
selected_eigenvectors = sorted_eigenvectors[:, :num_components]
# 데이터를 새로운 특징 공간으로 변환
transformed_data = np.dot(X_centered, selected_eigenvectors)
return transformed_data▶ PCA 실습 코드 예시
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
digits = load_digits()
X = digits.data
y = digits.target
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
plt.scatter(X_pca[:,0] , X_pca[:,1], c = y, cmap=plt.cm.get_cmap("jet", 10))
plt.colorbar(ticks=range(10))
plt.title("PCA")
plt.show()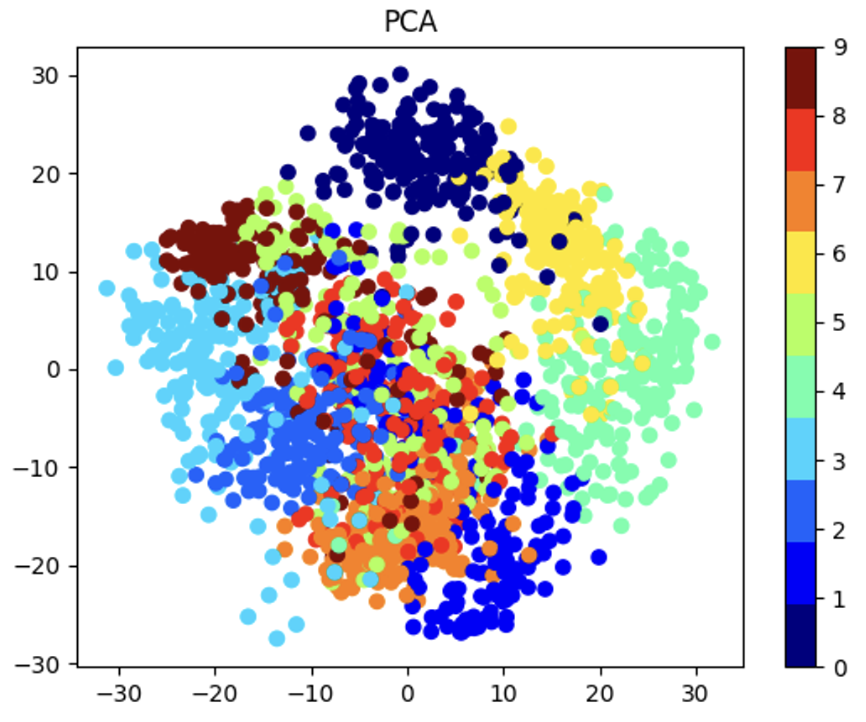
[출처 | 딥다이브 Code.zip 매거진]
