[논문] UniMotion: Unifying 3D Human Motion Synthesis and Understanding

재가 좋아하는 Real Virtual Human 연구소에서 새로운 논문 UniMotion: Unifying 3D Human Motion Synthesis and Understanding을 발표했습니다. 이미 많은 분야에서 사용하고 있는 Diffusion모델을 Motion쪽에도 적용하였습니다. 물론, 벌써부터 Text to Motion은 많이 연구되어오긴했는데, 아직은 뭔가 엉성한? 느낌이 없지 않아 있고, artifact들이 있었습니다. 그런데 이번에 소개할 논문은 그런 느낌을 최소화하는 방향과 동시에, 프레임 단위의 동작과 전체적인 동작이 잘 어우러지게 조작할 수 있도록 해주었습니다.

모델의 원리도 중요하지만, 데이터를 어떻게 사용했는지와 같은 디테일적인 면도 정말 필요하게 느껴졌는데, 그 내용은 supplementary Material을 통해서 알 수 있었습니다. 그 부분에서 연구자들이 얼마나 많은 시행착오를 했는지 알 수 있었습니다. 👏

https://arxiv.org/pdf/2409.15904
https://coral79.github.io/uni-motion/
https://github.com/Coral79/Unimotion

Introduction

: 생성 모델은 global한 목적을 인지하고 있는 동시에 local한 부수 task까지 수행하며, 어떤 행동이 언제 일어나는지 인지하고 있어야 한다. 하지만, 대부분의 연구들은 계층적인 조작이 어렵거나, 동작이 어설프고, frame별로 동작이 어려운 경우가 많다. 본 논문은 Unimotion을 제안하여, flexible한 동시에 frame level motion에 대한 이해가 가능하도록 하였다.

모델의 input은 전체적인(global), 세부적인(local) 모션에 대한 설명이나, 모션 시퀀스, 또는 일부, 심지어 없을 수 있다. 이에 따른 모델의 output은 세부적인 포즈 설명이나 모션 시퀀스가 될 수 있다. 이러한 flexibility는 Frame-Level Text-to-Motion, Sequence-Level Text-to-Motion and Motion-to-Text를 한번에 할 수 있음을 나타낸다. 더불어, frame-level로 모션을 만들수 있기도 하고, 모션 description을 만들 수 있다.

이 모델은 기본적으로 transformer 구조를 가지고 있다. 또한 UniDiffuser 방법론처럼, 각각의 다른 diffusion time variables을 이용하여, text와 pose를 같이 diffuse함으로써 개선하였다.

UniMotion: Unifying Motion Synthesis and Understanding

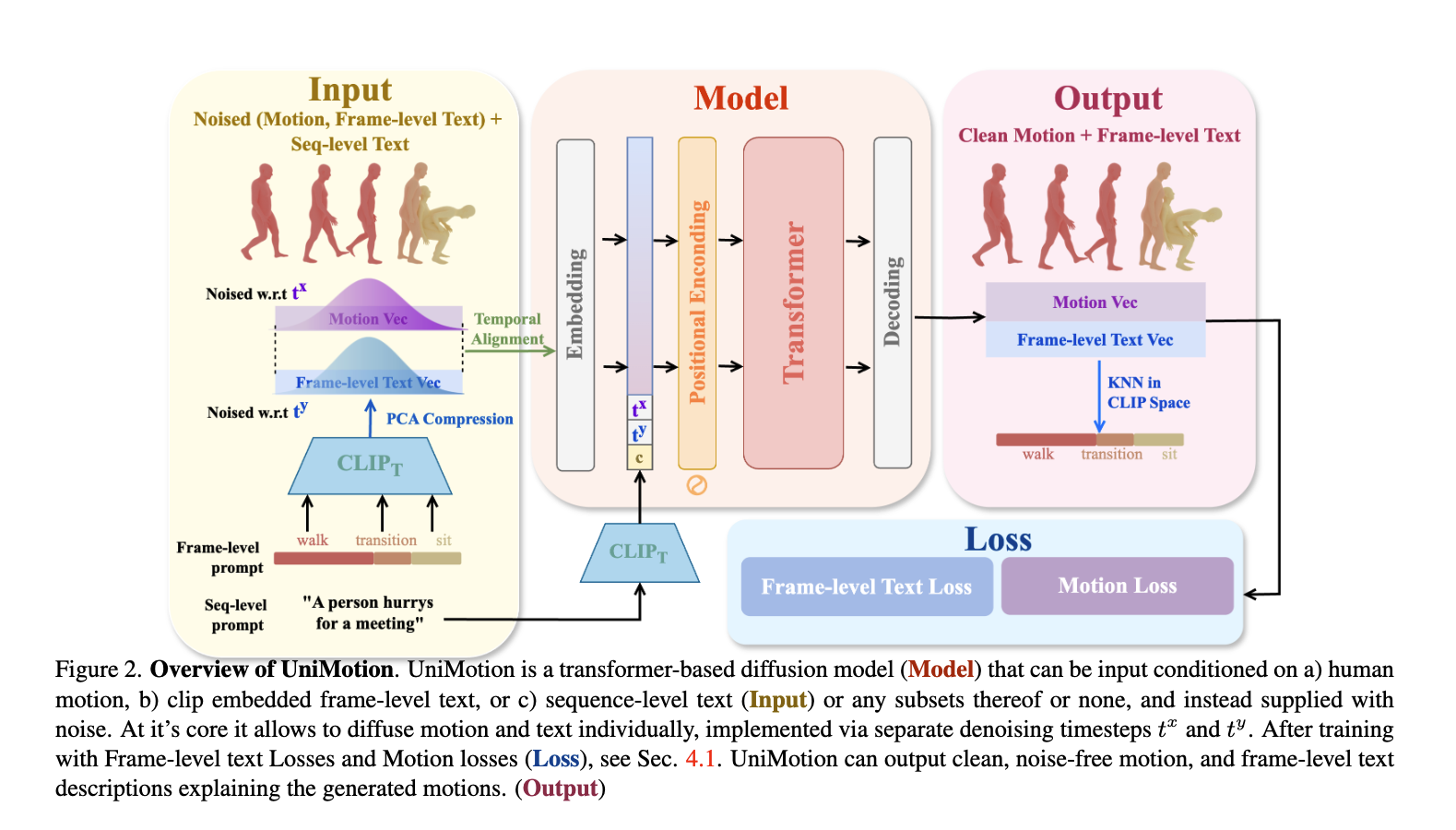
Multi-Modal Motion and Text Diffusion

• 기존 모델 (text-to-motion)들과 달리 motion과 text를 동시에, 즉 multi-modal로, 학습하고 생성하는 방식 제안
  • 모션 시퀀스 + 프레임 단위의 상세한 텍스트 정보 함께(동시에) 학습 가능
  • text와 motion을 함께 모델링하기 때문에 시간적 정렬 유지 가능
• 모델
  $G_{\theta} (\mathbf{x}_t^x, \mathbf{y}_t^y ; t^x, t^y, c)$
• $\mathbf{x}_t^x$: 노이즈가 추가된 모션 데이터
• $\mathbf{y}_t^y$ : 노이즈가 추가된 텍스트 데이터

Temporally aligned Text and Motion Encoding

• motion과 text를 하나로 묶어 input으로 사용하는 것이 핵심
  • 모션과 텍스트가 서로 독립적으로 입력하면, 연관성이 유지되지 않음.
  • Unidiffuser 방식: text의 각 token을 개별적으로 입력 (text를 시퀀스로 나눠 모션 처리)하는 방싱느 성능 저하가 생김
  • motion과 text를 시간축으로 결합하여 하나의 인풋으로 사용. 신경망이 text와 Motion의 정렬방식에 신결 쓸 필요가 없음!
• CLIP 기반의 embedding
  • 단순한 정렬은 최적의 성능 보장 불가하기 때문에 사용
  • text를 사전 학습된 CLIP 모델의 embedding 공간상의 vector로 변환
  • 그러나 CLIP 임베딩은 고차원의 벡터로 변환시키기 때문에, PCA를 추가하여 50차원으로 줄임.
• 최종 텍스트 라벨 복원
  • diffusion의 출력을 CLIP 임베딩으로 변환
  • 모델이 생성한 CLIP 임베딩을 기존의 텍스트 베이스와 비교하여 가장 가까운 텍스트를 매칭. (생성된 벡터와 가장 유사한 기존 라벨 매칭 방식. KNN)

Data Merging

• AMASS가 메인 데이터
  • BUT, 모션만 있고 Text 없어서 BABEL, HumanML3D도 사용
    • BABEL: 프레임 단위 text
    • HumanML3D: 시퀀스 단위 text
• 학습 방법
  • frame단위와 sequence단위 라벨을 함께 정렬 (특정 경우는 하나만 사용하기도 함)

Supplementary Material

Trainig Data

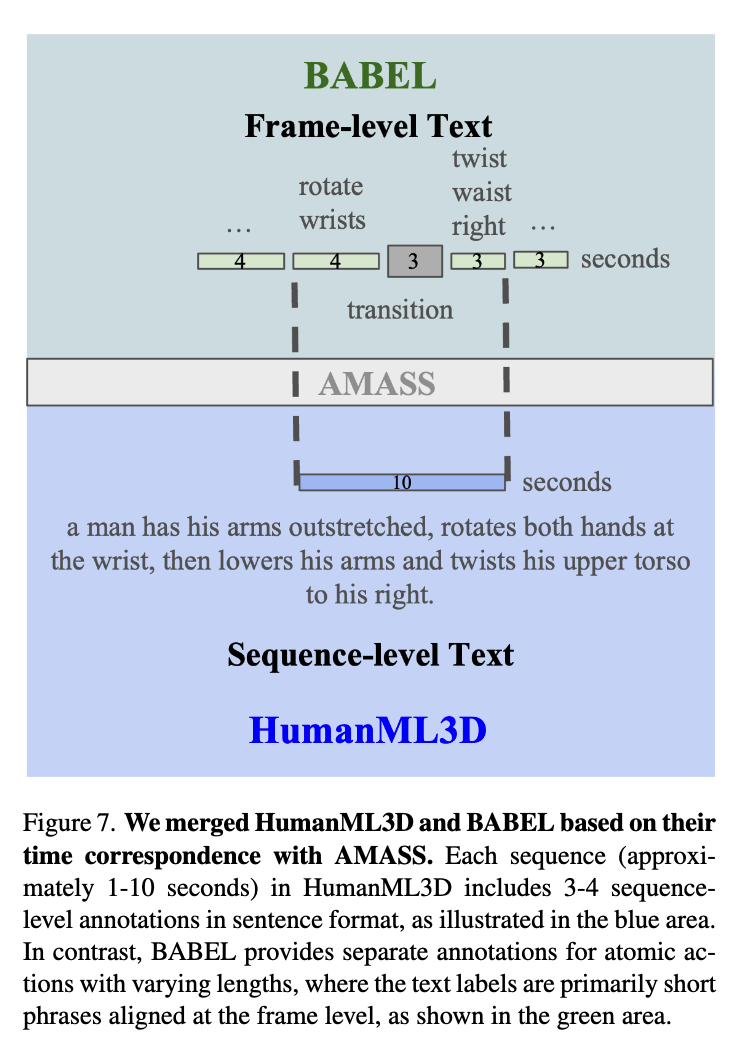
학습에 사용한 BABEL(frame-level)과 HumanML3D(sequence-level)의 공통 데이터는 8,829 시퀀스로, HumanML3D 전체의 30.25%밖에 되자 않았습니다.

Implementation Details

(모델 구현에 대한 세부정보)

• MDM을 확장.
• 모션과 frame-level의 모션과 텍스트를 timestep에 따라 나눠서 학습.
• 병합된 데이터(두 데이터셋에 공통된 부분)를 스크래치로 재학습. (하이퍼 파라미터는 MDM과 동일)
• frame-level text는 MDM과 같은 CLIP사용해서 embedding 생성 -> PCA사용하여 256차원에서 51차원으로 축소.(원 variance의 70% 보존) -> KNN 적용하여 output CLIP embedding에 대하여 미리 저장된 데이터 베이스에서 가까운 embedding 찾음.
• Algorithm 1: Training

1. repeat:
2.    샘플링: x₀, y₀, c ~ q(x₀, y₀, c)
3.    확률적으로 c를 비움 (10% 확률)
4.    t 값을 Uniform(1, 2, ..., T) 에서 무작위 선택
5.    정규분포에서 노이즈 샘플링: εˣ, εʸ ~ 𝒩(0, I)
6.    노이즈 추가:
      xₜ = √ᾱₜ * x₀ + √(1 - ᾱₜ) * εˣ
      yₜ = √ᾱₜ * y₀ + √(1 - ᾱₜ) * εʸ
7.    모델을 학습하기 위한 그래디언트 스텝 수행:
      ∇θ|ℓθ(xₜ, yₜ, t, c) - [x₀, y₀]|²
8. until (수렴할 때까지 반복)

• Algorithm 2: Sampling x₀ conditioned on y₀

1. 샘플링: xₜ⁰ ~ 𝒩(0, I)
2. 조건 설정: c = ⌀ (또는 사용자가 지정)
3. for t = T, ..., 1 do:
4.     정규분포에서 노이즈 샘플링: εₜˣ ~ 𝒩(0, I)
5.     업데이트 공식:
       xₜ₋₁⁰ = εθ(√ᾱₜ * xₜ⁰ + √(1 - ᾱₜ) * εₜˣ, y₀, t, c)
6. end for
7. return x₀

• Algorithm 3: Joint Sampling of x₀, y₀

# Algorithm 3: Joint Sampling of x₀, y₀
1. 샘플링: xₜ⁰, yₜ⁰ ~ 𝒩(0, I)
2. 조건 설정: c = ⌀ (또는 사용자가 지정)
3. for t = T, ..., 1 do:
4.     정규분포에서 노이즈 샘플링: εₜˣ, εₜʸ ~ 𝒩(0, I)
5.     업데이트 공식:
       xₜ₋₁⁰ = εθ(√ᾱₜ * xₜ⁰ + √(1 - ᾱₜ) * εₜˣ, t, c)
       yₜ₋₁⁰ = εθ(√ᾱₜ * yₜ⁰ + √(1 - ᾱₜ) * εₜʸ, t, c)
6. end for
7. return x₀, y₀

More Applications

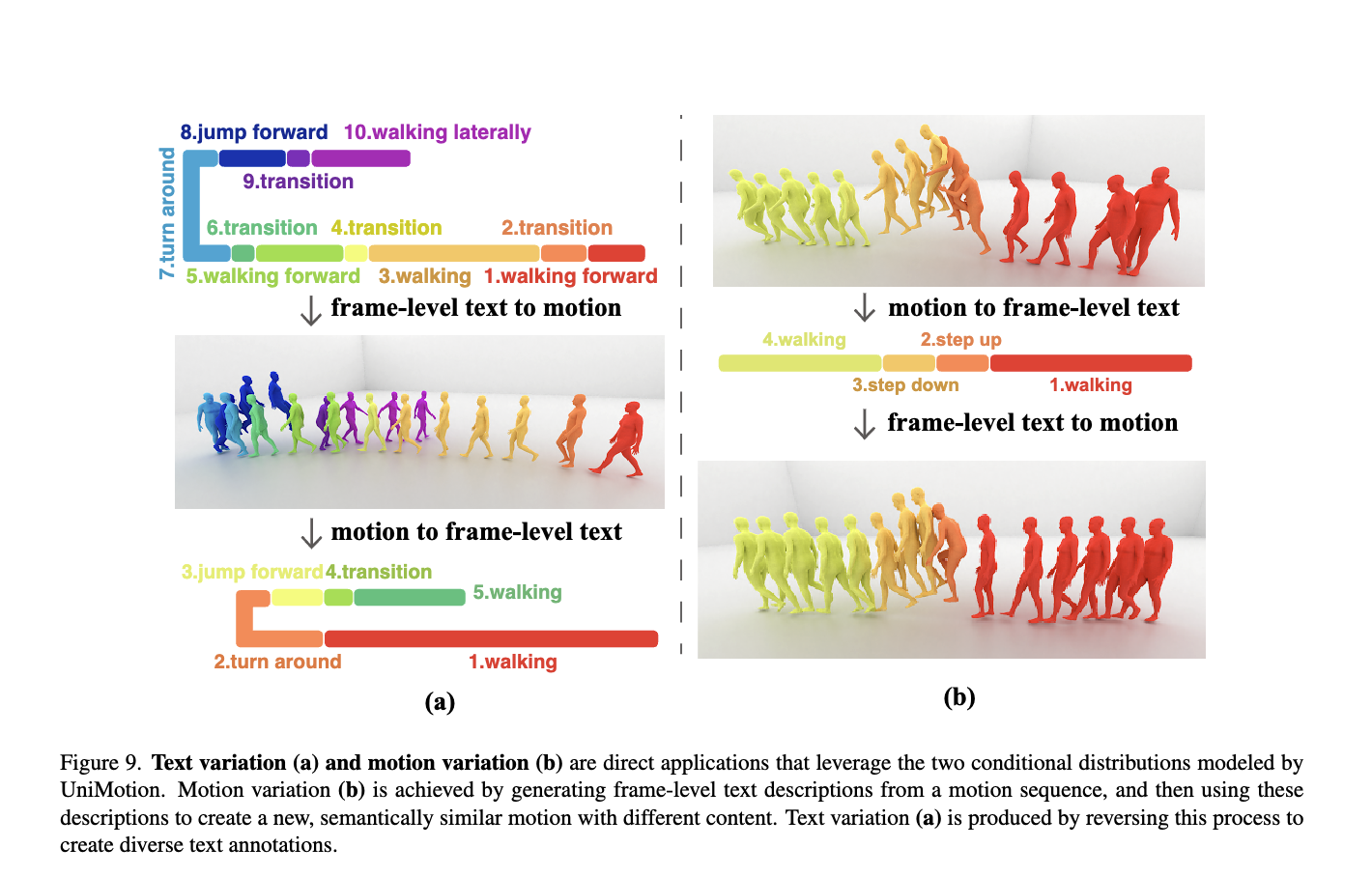
• 다양하게 응용 가능
  • 모션 변형: 주어진 모션 시퀀스에 대해 motion understanding 작업으로 frame-level로 text를 만들고, 이것을 활용해서 다시 모션을 만들면 기존과 비슷하지만 변형된 결과를 만들 수 있음.
  • 텍스트 변형: 모션 변형을 반대로 적용

Motion-to-text Understanding Baselines

• LLM(GPT)사용 시도: 시퀀스를 프레임단위로 나누는 것이 가능하나, 정보가 불완전하고, 프레임 인덱스를 구분하는 것이 신뢰할 수 있는 정도가 아니여서 사용 못 함.
• Motion GPT 사용 시도: 모션 데이터와 text prompts를 함께 쓸 수 있지만, 정보의 신뢰도가 떨어져 사용할 수 없었음.