이전 논문에서 Mask를 사용하는 tranformer를 사용하여 퀄리티를 높이는 text-to-motion 연구를 봤었는데요. 그 논문보다 성능이 좋지는 못하지만 굉장히 유사한 방법을 사용했길래 살펴보게되었습니다. 이전 논문이 정말 세심한 기법들을 사용해서 그런지 이 연구가 조금은 아쉽기도 했는데요...그래도! 뭐에 더 집중하고 싶었는지를 잘 보여주는 것 같고, 또 뭔가 설명이 친절해서 text-to-motion의 전체적인 연구동향을 알기가 쉬웠다는 점도 있습니다. ㅎㅎㅎ(뭔가 표현이 이 연구에 대해 부정적인 것 같은데 절대 그렇지 않아요!! 이걸 먼저 읽었으면 이전 논문 이핵 더 빨랐을 거 같긴하네요 ㅋㅋㅋ) 그래도 CVPR 2024중에 Highlight로 선정된 논문입니다!!!!
https://arxiv.org/pdf/2312.03596
https://exitudio.github.io/MMM-page/
https://github.com/exitudio/MMM/
Introduction
저자들은 다른 연구들에서 제안했던 방식들이 품질이 별로거나, 속도가 느리거나 모션 편집이 불가능하다는 단점들을 모두 만족시킬 수 있는 방법을 제한하려합니다.
- 다른 연구들
- 언어와 모션의 latent 정렬
- 속도는 빠르나, 세밀한 정보를 잃음
- Conditional Diffusion Model
- 품질은 좋으나 속도가 느림
- Conditional Autoregressive Model
- 속도가 빠르지만 디테일이 아쉬움
그래서 저자들은 실시간 성능, 퀄리티, 편집 가능성이 다 가능한 MMM을 제안합니다.
- 언어와 모션의 latent 정렬
- MMM
- VQ-VAE 기반 motion tokenizer를 pretrain하여, 3D 모션을 discrete token sequence로 변환.
- 일부 토큰을 무작위로 마스킹 후, conditional masked transformer를 사용하여 복원하도록 함.
- 장점
- parallel decoding: autoregressive대비 빠름
- bidirectional: diffusio보다 더 자연스러운 모션
- editability: inbetweening 가능
Method
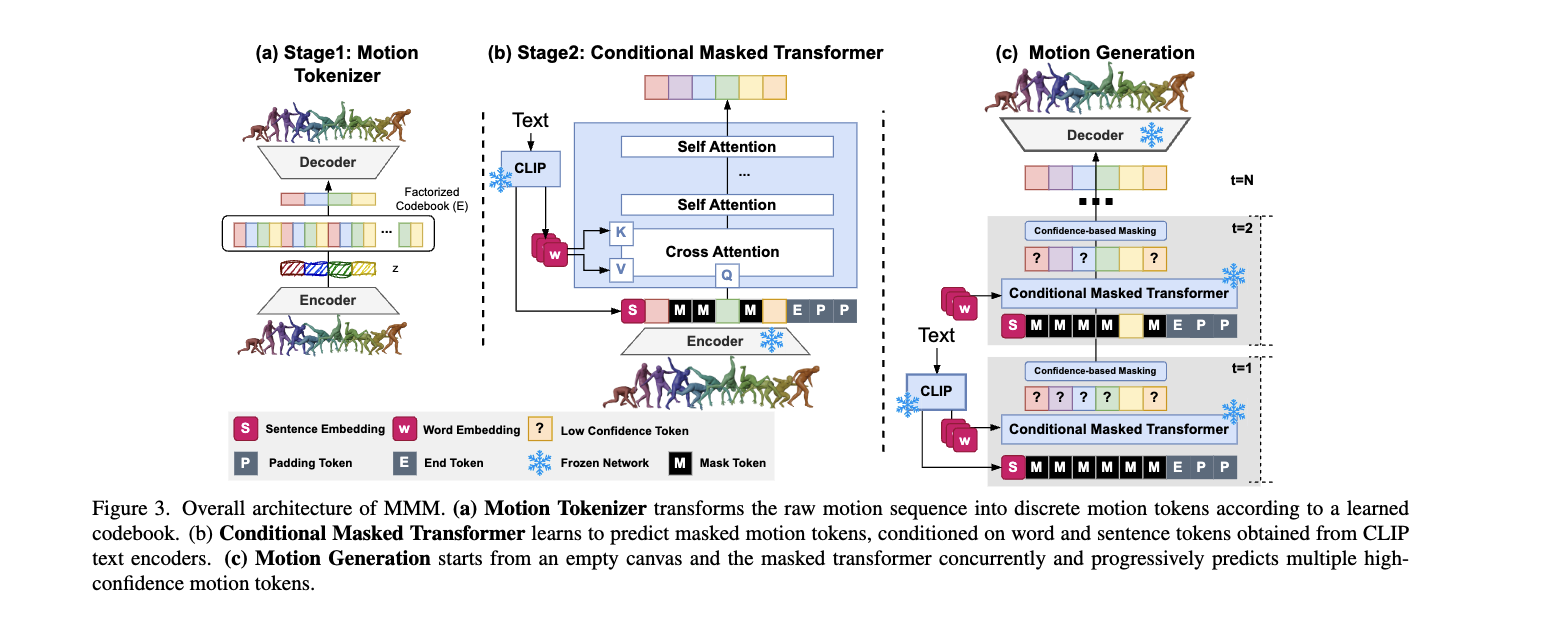
- 목표: 품질좋고 빠르고 편집 가능한 text-to-motion
- 구성: Motion Tokenizer, conditional masked motion transformer
Motion Tokenizer
- vector quantization의 objective:
- : stop-gradient, : commitment loss parameter, : codebook vector from Codebook
- embedding 는 아래 방식(유크리드 거리)으로
- Codebook 사이즈: 8192
- 실험해봤는데, 크면 모션 품질이 올라감 (단, 너무 크면 codebook collapse 발생할 수 있음)
- codebook collapse: 대부분의 token이 소수의 code에만 집중되고, 나머지 항목들은 비활성화되는 문제
- 실험해봤는데, 크면 모션 품질이 올라감 (단, 너무 크면 codebook collapse 발생할 수 있음)
- factorized code방식인 code lookup과 code embedding 분리를 통해 codebook을 안정화하고 활용도를 높임
- moving average방식으로 코드북의 update와 reset
Conditional Masked Motion Model
Text-conditioned Masked Transformer
- Input: motion token sequence, text embeddings, special-purpose tokens
- text embeddings
- sentence embedding: CLIP 모델을 사용하여 얻은 문자 전체를 의미를 가진 임베딩
- word embedding: 개별 단어들의 임베딩
- 단어별로 모션과 연결될 수 있도록 Cross-Attention 을 적용함.
- 단어별로 모션과 연결될 수 있도록 Cross-Attention 을 적용함.
- special-purpose tokens
- [MASK], [PAD], [END] 등을 포함하여 학습을 돕는 토큰
- MASK: 일부 모션 토큰을 가리고, 모델이 이를 채우도록 유도
- PAD: 다양한 길이의 모션 시퀀스를 고정된 길이로 맞추기 위한 패딩. 짧은 데이터는 [PAD]로 채워져 모델이 일정한 입력을 받을 수 있도록
- END: 생성된 모션이 불필요하게 길어지는 것을 방지
Training Strategy and Loss
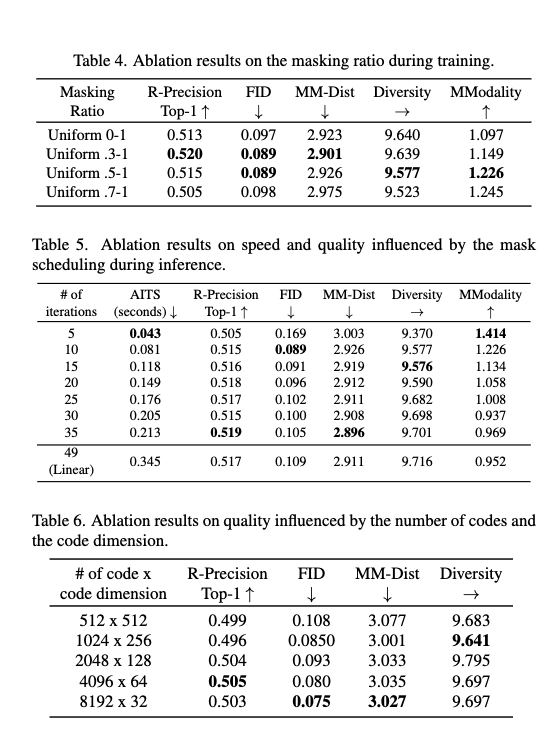
- 모션 토큰 시퀀스 에서 개를 masking하고 해당부분은 [Mask] 토큰으로 대체하여 corrupted motion sequence 으로 만들어냄. (: masking ratio, )
- corrupted motion sequence 과 text embedding 를 text-conditioned masked transformer에 통과하여 아래 loss를 적용하며 복원하도록 한다.
Inference via Parallel Decoding
- 추론 과정에서 모션 토큰을 디코딩하기 위해, 모든 [MASK] 토큰을 입력
- 모든 [MASK] 토큰: 비어있는 캔버스, 반복을 통해 점차 많은 토큰 예측.
- 반복적인 병렬 디코딩(iterative parallel decoding)
- 각 반복(iteration)에서 트랜스포머는 모델이 가장 신뢰도가 낮은(confidence가 낮은) 모션 토큰의 일부를 마스킹한 후, 다음 반복에서 이 마스킹된 토큰들을 병렬로 예측
- 마스킹 개수
- 선형적 감소 스케줄과 비교해보았으나, 위 방식이 더 나음.
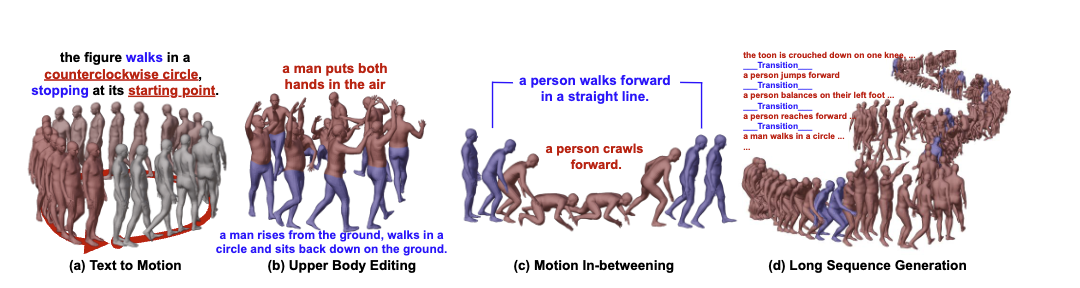
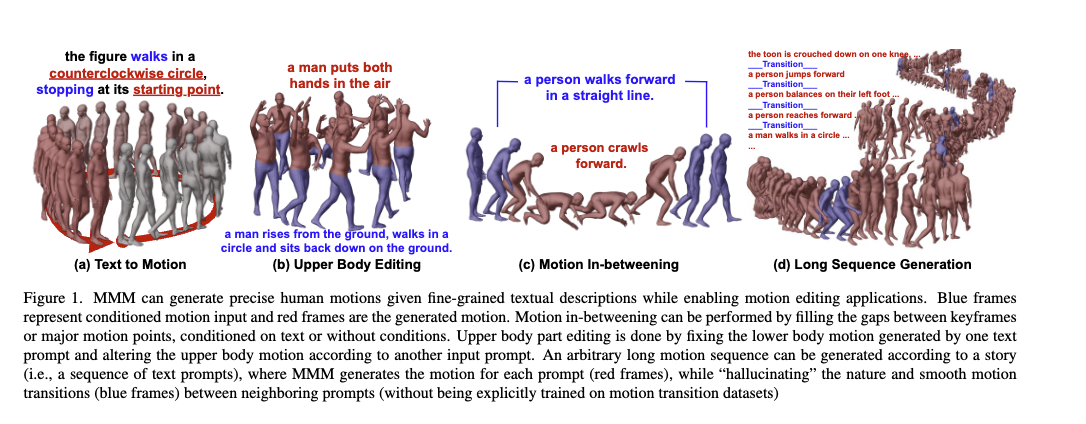
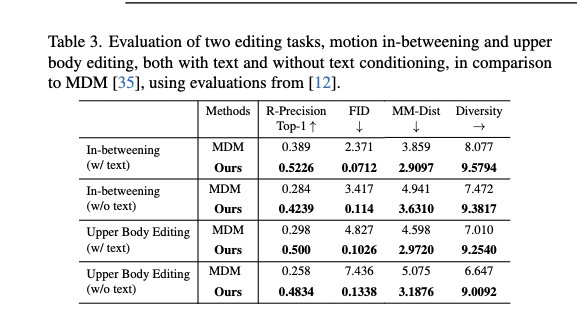
Motion Editing
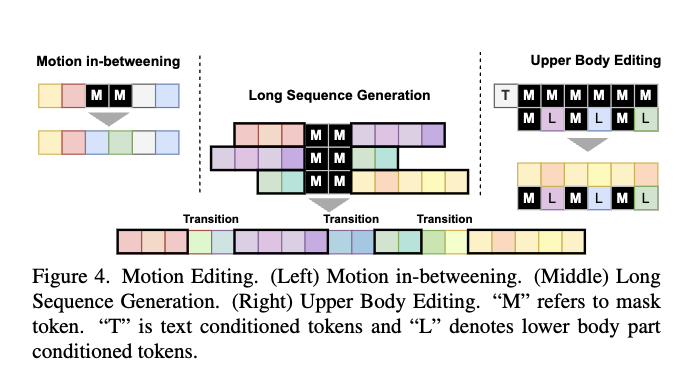
위 이미지처럼 다양한 편집이 가능
Motion In-betweening
- 원하는 위치에 [MASK] 토큰을 배치하여 편집 수행
Long Sequence Generation
- 여러 개의 text prompts로 구성된 스토리가 주어지면, 모델은 각 프롬프트에 대한 모션 토큰 시퀀스를 먼저 생성
- 그 후, 이전 모션 시퀀스의 끝과 다음 모션 시퀀스의 시작을 조건으로 하여, transition motion tokens을 생성
Upper Body Editing
- upper body와 lower body 부분의 tokenizer를 개별적으로 pretrain
- 상체 토큰과 하체 토큰을 다시 concatenate하여 full-body 임베딩을 형성
- 하체 모션 시퀀스에 일부 [MASK] 토큰을 무작위로 삽입하여 light corruption 주며, 이를 통해 트랜스포머가 전신 모션의 spatial & temporal 의존성을 더 효과적으로 학습
- Loss
- L{up} = - \mathbb{E}{Y \sim D} \left[ \sum_{i \in {1, L}} \log p\left( y_i^{up} | Y_M^{up}, Y_M^{down}, X \right) \right]
Experiments
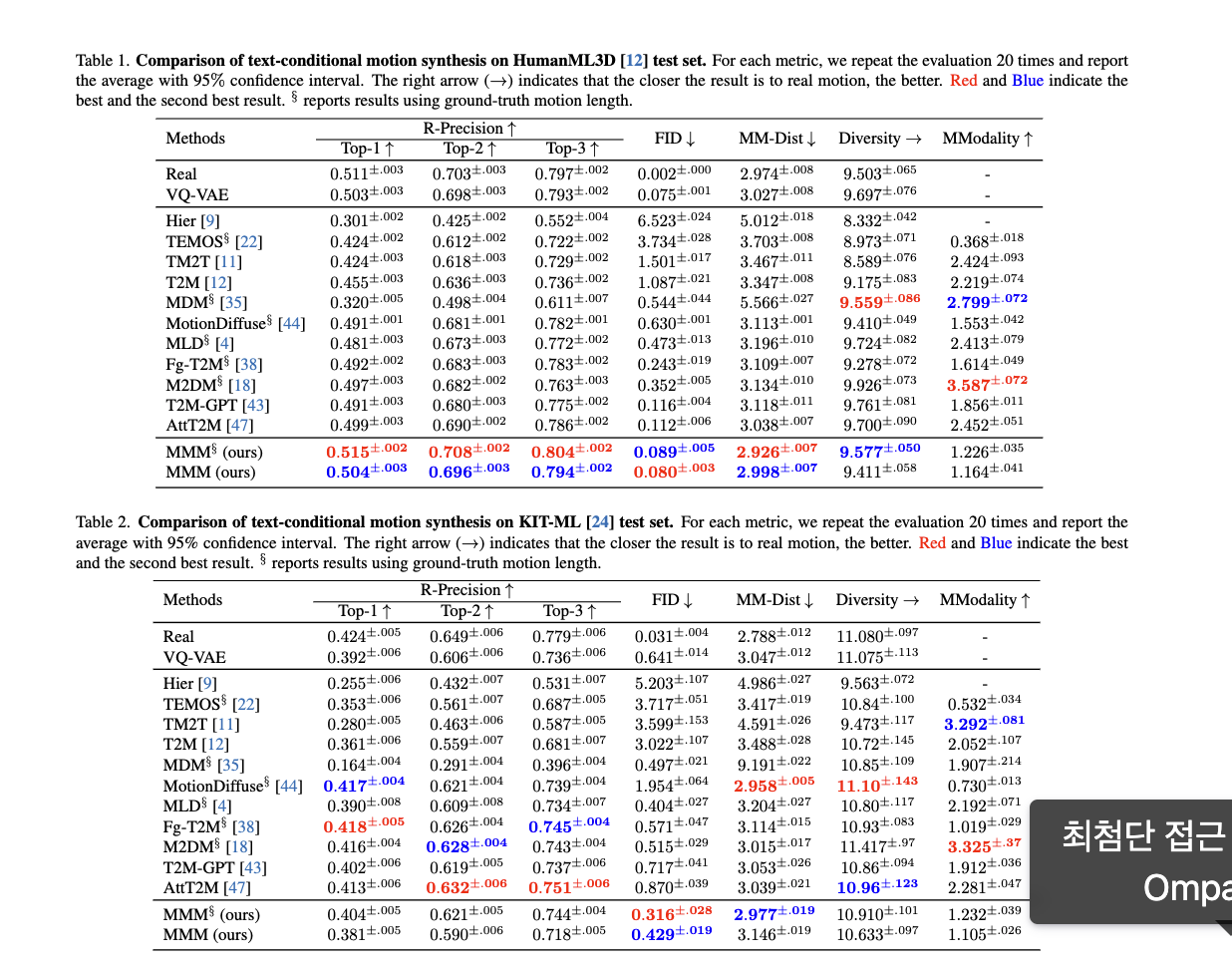
- Dataset: HumanML3D, KIT-ML
- Evaluation Metrics: R-precision, Multimodal Distance (MM-Dist), Frechet Inception Distance (FID), MultiModality (MModality)
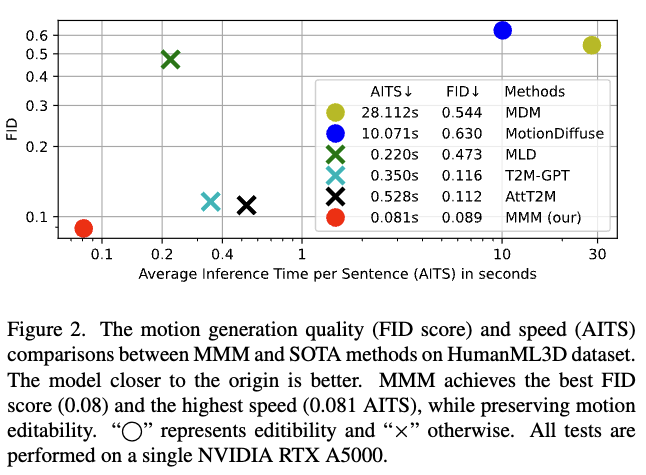
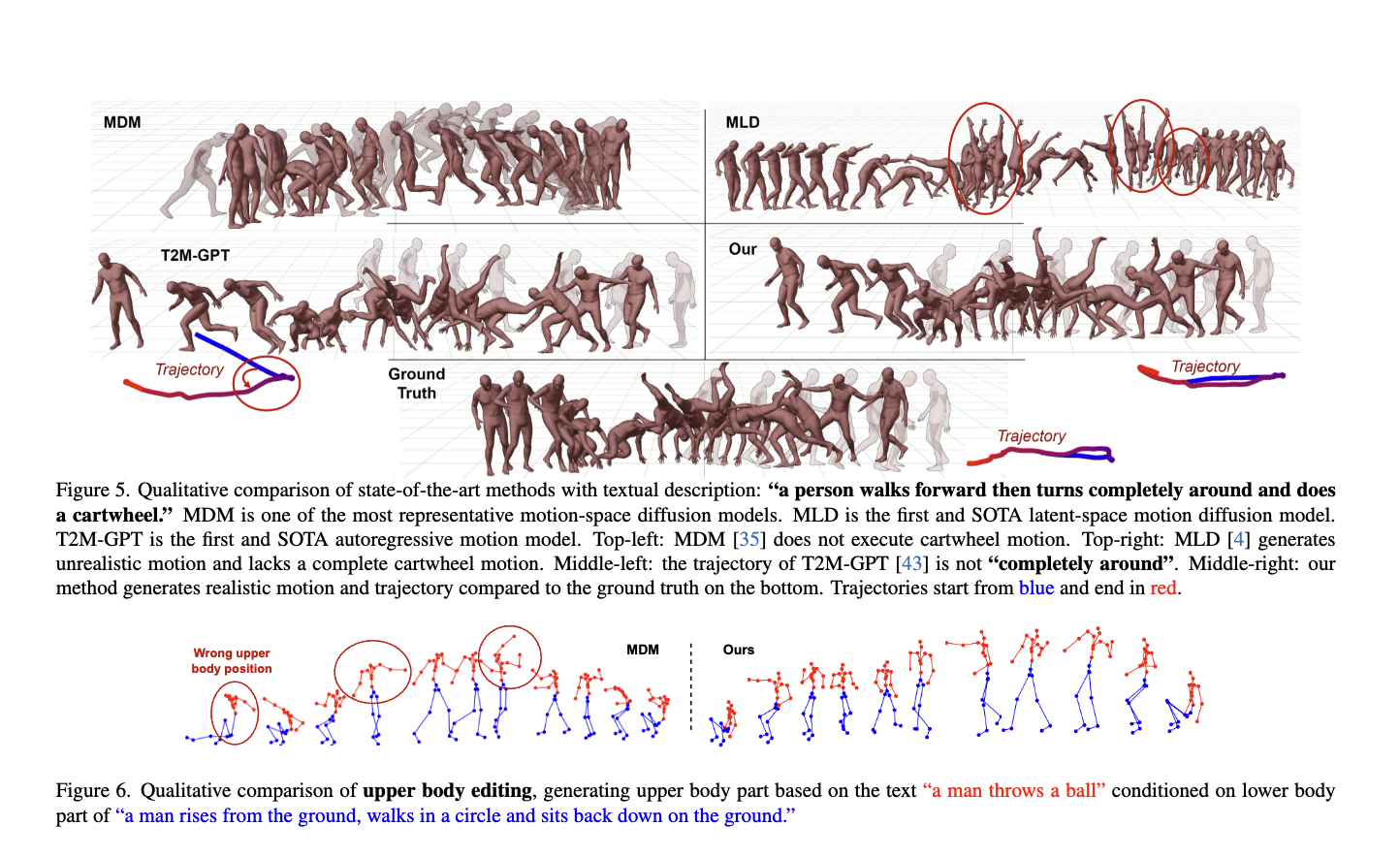
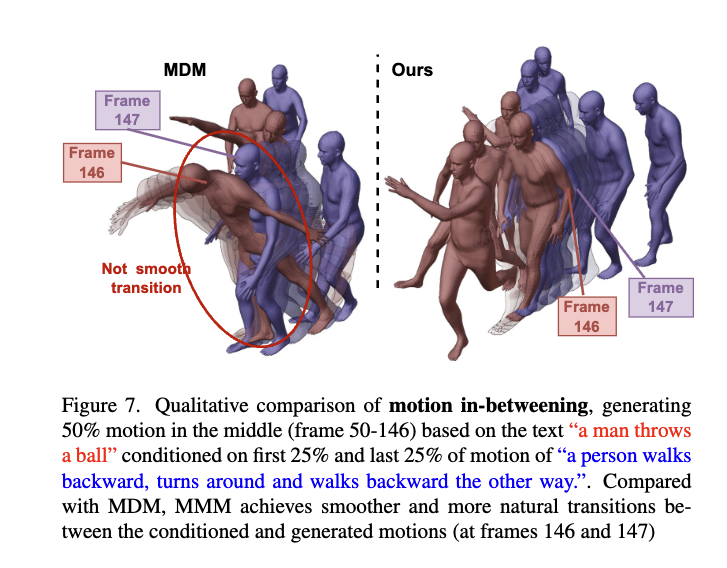
Comparison to State-of-the-art Approaches
Ablation Study