[논문] MDM, Motion Diffusion Model

diffusion이 큰 화제가 되면서 (된지는 좀 됐죠? ^^), motion 생성에도 쓰이기 시작했는데요! 이후에 계속 나온 motion generation 분야에서 기초가 되기도하고, 또는 테스트 비교 대상이 되는 MDM 논문을 소개해봅니다. 이 논문의 가장 큰 포인트는 노이즈를 예측하는 것이 아닌 점에 있는데, 이런 핵심 아이디어가 MDM의 시작이 아닐까 생각해봅니다 ㅎㅎ

https://arxiv.org/pdf/2209.14916.pdf
https://guytevet.github.io/mdm-page/
https://github.com/GuyTevet/motion-diffusion-model
https://replicate.com/daanelson/motion_diffusion_model

Introduction

모션 생성은 many-to-many 매핑 문제로 봐야합니다. 논문의 예를 인용하자면, "kick"은 축구의 발차기를 의미할 수도 있지만, 카라테의 발차기가 될 수 도 있기 때문이죠(위 그림 참조). 하지만, text-to-motion 연구들의 대부분은 Auto-Encoder또는 VAE를 사용하기 때문에, 학습된 분포 속에서 one-to-one 매핑 또는 정규 분포로 제한되죠. 이런 문제를 저자들은 target distribution으로 부터 자유로운 diffusion model을 이용하여 해결하였습니다.
단, diffusion에게도 단점은 있습니다. 일단 리소스가 많이들어가고, 제어도 어렵기 때문이죠. 저자들은 이 어려움에도 불구하고 아래와 같은 특징을 가진 최대한 효율적이고 정교한 모델을 개발합니다.

• UNet이 아닌 transformer 기반의 backbone 사용
  • ligthweight(비교적 가볍고), temporal & non-spatial의 특징을 가진 모션 데이터에 적합
• Geometric loss를 이용하여, 속도 조절과 발 미끄러짐을 제어.
• 다양한 형태의 conditioned 생성 가능 (다양한 기능 지원)
  • text-to-motion, action-to-motion, unconditioned motion generation
• classifier-free manner를 이용한 다양성과 정확성의 밸런싱

위와 같은 특징으로, HumanML3D와 KIT에서 SOTA성능을 달성했고, 심지어 정성평가에서 42%의 심사자들이 MDM의 결과물을 더 선호했다고 합니다.

Motion Diffusion Model

• 모델의 목표: 조건 $c$에 따라 길이 $N$의 인간 모션 $x_{1:N}$을 생성. (조건이 없는 경우도 포함)
  • $x_{1:N} = {x_i}_{i=1}^{N}$ : generated pose sequence
  • $x_i \in \mathbb{R}^{J \times D}$, $J$: joint개수, $D$: dimension of joint representation.
  • pose 표현 방식: location / ratation / (location, roation)

Framework

• Diffusion은 Markov noisiong process에 따라 모델링 된 것.

  • $q(x_{1:N}^{t} | x_{1:N}^{t-1}) = \mathcal{N} \left( \sqrt{\alpha_t} x_{1:N}^{t-1}, (1 - \alpha_t) I \right)$

    • $\{x^{1:N}_t\}_{t=0}^{T}$: difffusion 과정에서 $t=0$부터 $t=T$까지 변하는 모든 $x_t^{1:N}$ 들의 모음.
    • $x_t^{1:N}$ : 시간 $t$ 에서의 모션 시퀀스(전체 프레임)
    • $\alpha_t \in (0,1)$: 고정된 하이퍼파라미터

  • 위 수식에서, $\alpha_t$ 가 아주 작으면 $x_{1:N}^{T}$ 는 정규분포 $\mathcal{N}(0, I)$ 에 가까워지고, 이후부터는 노이즈 단계 $t$ 스텝에서의 전체 시퀀스를 $x_t$ 로

• 모션 생성에 있어서는 $p(x_0 | c)$ 를 reverse diffusion process로 모델링하며, 이는 노이즈가 많은 $x_T$ 를 점진적으로 깨끗한 데이터로 변환하는 과정.

• 기존 diffusion 처럼, 역방향 과정에서 노이즈를 예측하는 것이 아닌 signal 자체를 예측하는 방식. $\hat{x_0}=G(x_t,t,c)$

• 손실함수 $L_{simple}$

  • $L_{\text{simple}} = \mathbb{E}_{x_0 \sim q(x_0 | c), t \sim [1, T]} \left[ \| x_0 - G(x_t, t, c) \|^2_2 \right]$

Geometric Losses

• 전체 Loss

  • $L = L_{\text{simple}} + \lambda_{\text{pos}} L_{\text{pos}} + \lambda_{\text{vel}} L_{\text{vel}} + \lambda_{\text{foot}} L_{\text{foot}}$

• $L_{\text{pos}} = \frac{1}{N} \sum_{i=1}^{N} \| FK(x_i^0) - FK(\hat{x}_i^0) \|_2^2$

  • 예측된 관절 위치가 원본과 잘 align 되도록
  • $FK(\cdot)$ : rotation을 positiondm로 변환하는 forward kinematic function

• $L_{\text{foot}} = \frac{1}{N - 1} \sum_{i=1}^{N-1} \| (FK(\hat{x}_{i+1}^0) - FK(\hat{x}_i^0)) \cdot f_i \|_2^2$

  • 발이 지면에 닿았을 때 속도를 0으로 만들어 발 미끄러짐(foot-sliding) 현상을 완화

• $L_{\text{vel}} = \frac{1}{N - 1} \sum_{i=1}^{N-1} \| (x_{i+1}^0 - x_i^0) - (\hat{x}_{i+1}^0 - \hat{x}_i^0) \|_2^2$

  • 예측된 모션의 속도가 원본 모션과 일관되도록

Model

• 모델 $G$ : 단순한 Transformer기반의 인코더 전용(encoder-only) 아키텍처

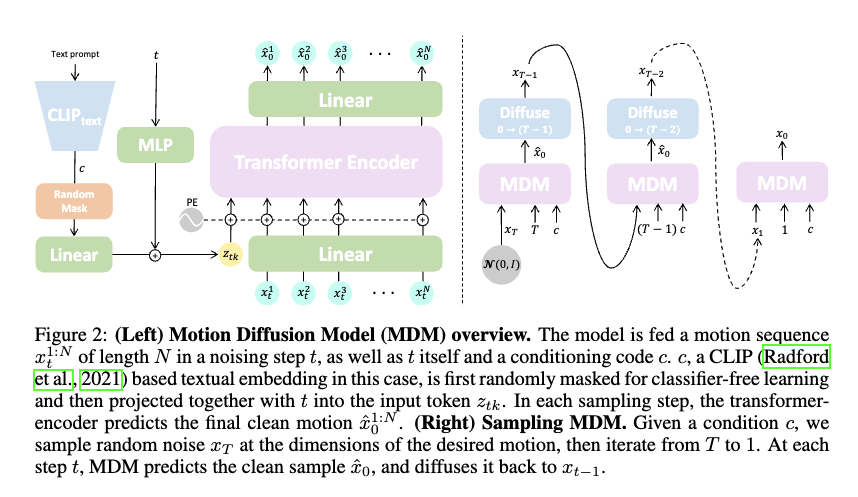
• 과정(이미지 참조):

  • 노이즈 time step $t$와 condition $c$가 각각 feed-forward network를 통해 Transformer 차원으로 projection되며, 이후 합산되어 토큰 $z_t^k$ 를 생성.

    • $z_t^k = \text{FFN}_t(t) + \text{FFN}_c(c)$

  • 노이즈가 추가된 입력 $x_t$ 의 각 프레임은 Transformer 차원으로 linear projection되며, positional embedding과 합쳐진다.

  • 이후 $z_t^k$ 와 변환된 프레임들이 Transformer 인코더에 입력

  • 인코더 출력에서 첫 번째 토큰($z_t^k$에 해당)을 제외한 나머지는 원래의 모션 차원으로 다시 변환되며, 최종적으로 예측된 $\hat{x}_0$
    가 됨

    • $\hat{x}_0 = \text{Proj}(\text{Encoder}(z_t^k, x_t))$

  • CLIP 텍스트 인코더를 사용하여 텍스트 프롬프트를 $c$ 로 인코딩함으로써 text-to-motion 변환을 구현하며, 각 클래스별 학습된 임베딩을 이용하여 action-to-motion 변환을 구현한다.

Sampling

• 각 시간 스텝 $t$ 마다, 모델은 깨끗한 모션 샘플 $\hat{x}_0 = G(x_t, t, c)$ 를 예측한 후, 다시 노이즈를 추가하여 $x_{t-1}$ 로 변환($t=T$ 부터 시작하여 $x_0$ 에 도달할 때까지 반복)
• 모델 $G$는 classifier-free guidance를 활용하여, conditional과 unconditioned 분포를 동시에 학습
  • 샘플의 10%에 대해 $c = \emptyset$ (조건이 없음)으로 설정하여 $G(x_t, t, \emptyset)$ 가 $p(x_0)$ 를 근사하도록 학습
  • 그 후, 샘플링 시에는 두 가지 방식을 interpolation 또는 extrapolation하여 다양성과 정확성 간의 균형을 조정
• $G_s(x_t, t, c) = G(x_t, t, \emptyset) + s \cdot (G(x_t, t, c) - G(x_t, t, \emptyset))$

Editing

• 연구자들은 시간적인 면에서 특정 부분의 모션을 보간하는 기능과 신체 일부만을 편집하는 기능 추가
  • 편집은 학습과정 없이 샘플링중에 이뤄짐.
  • 모션 시퀀스의 일부가 주어졌을 때, 각 iteration 마다 모델이 예측한 $\hat{x}_0$ 를 원본 모션의 일부로 덮어쓴다. -> 보간 효과

Experiments

• $T=1000$의 노이즈 스텝과 코사인 노이즈 스케줄로 학습
• NVIDIA GeForce RTX 2080 Ti GPU 한 대로 3일 학습

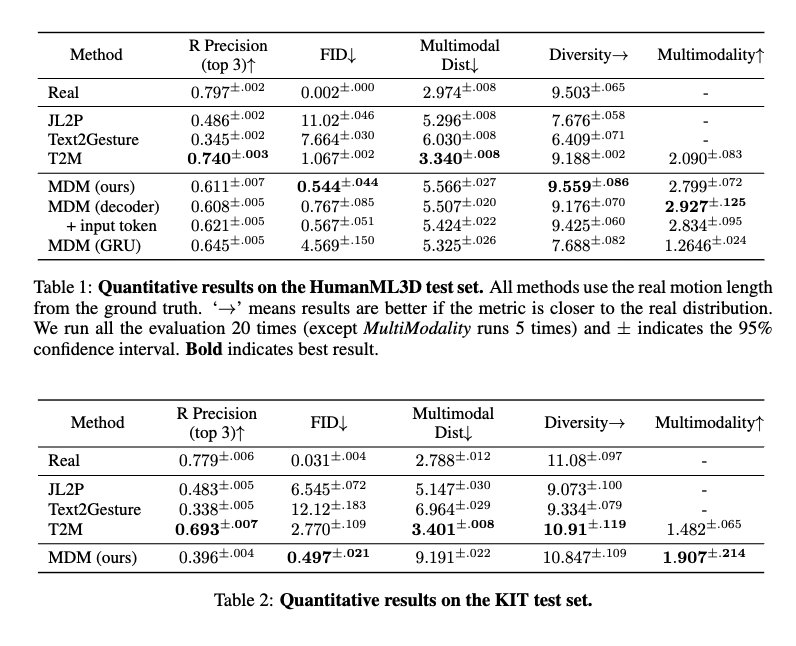
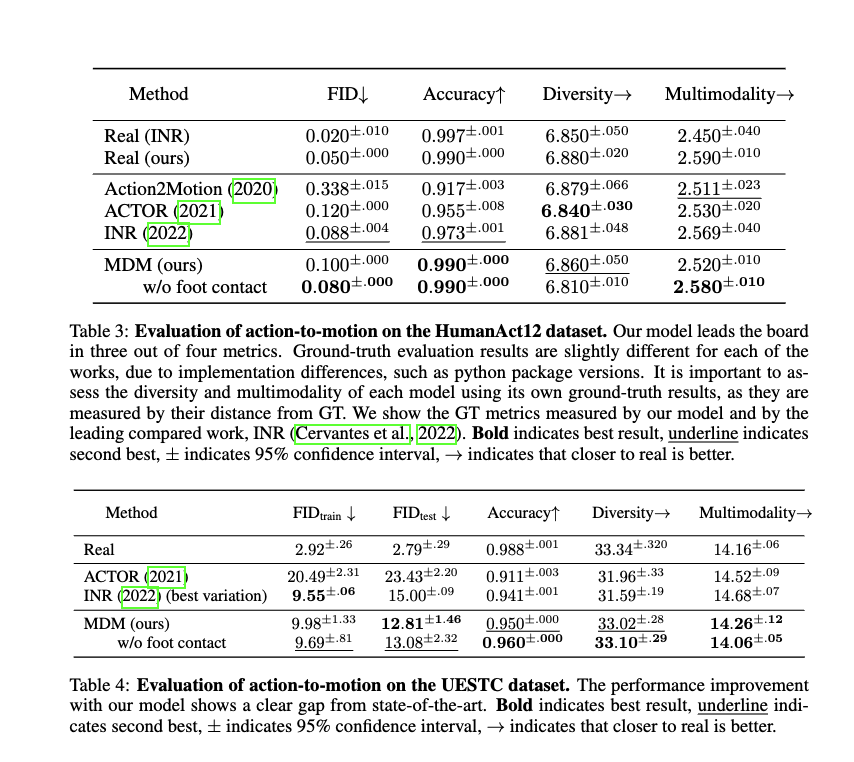
• KIT와 HumanML3D에서 사용한 평가지표 사용 (Guo et al.)
  • R-precision
  • Multimodal-Dist
  • FID: 생성된 모션 분포와 GT 모션 분포의 연관성
  • Diversity: 생성된 모션분포의 다양성
  • MultiModality: 하나의 프로폼트에서 생성된 모션들의 평균 분산

Data

• HumanML3D: AMASS 와 HumanAct12에 텍스트, 루트 속도, 관절 위치, 관절 속도, 관절 회전, 발접촉 정보 추가
• KIT