[231N] Assignment 1 - SVM
과제 1 의 두번째 코드인 SVM을 시작해보려 한다.
일단 CIFAR-10 Data Loading and Preprocessing 부분을 모두 실행한다.
데이터를 train, valid, test로 나누고 32,32,3 크기를 3072로 합친다.
그리고 추가적으로 development set을 만든다.
이는 train set에서 500개를 랜덤으로 고른 것이다.
Preprocessing 과정에서는
1. 평균을 계산한다.
2. train, val, test, dev set 모두 평균을 뺀다.
3. bias trick 를 추가한다.
SVM Classifier
여기서 이제 linear_svm.py를 수정해야한다.
일단 loss는 구현되어있고, 이제 기울기를 구해야한다. svm_loss_naive를 수정하면 된다.
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in range(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in range(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
loss += margin
dW[:, y[i]] -= X[i]
dW[:, j] += X[i]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += reg * np.sum(W * W)
dW += reg * 2 * W이렇게 dW를 구했다.
사실 dW를 갑자기 구하라니 너무 어렵게 생각했는데 일단
를 각각 편미분하면 된다.

편미분한 것은 위 두번째, 세번째 공식에 있다. 사실 편미분을 어떻게하는지는 나도 잘 모른다ㅠ 그냥 저 공식을 이용하자.
dW[:j] 는 Wj에 대한 편미분, dW[:y[i]]는 yi에 대한 편미분으로
각각 xi, -xi를 나타내서 sum하는 것이다...
dW[:, y[i]] -= X[i]
dW[:, j] += X[i]근데 for j의 반복문 내에서 실행되고 있기 때문에 y[i]는 margin이 0보다 큰 개수만큼 xi를 더하게 된다. (공식대로)
그리고 나누는 것은 미분도 마찬가지이고
regularization에서 를 미분하면 2W가 된다.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += reg * np.sum(W * W)
dW += reg * 2 * W잘 기울기을 계산했는지 확인하는 코드를 실행하면
numerical: 13.558055 analytic: 13.558055, relative error: 2.078249e-11
numerical: 10.319701 analytic: 10.319701, relative error: 6.520262e-11
numerical: -8.430116 analytic: -8.430116, relative error: 4.154574e-11
numerical: -24.947223 analytic: -24.947223, relative error: 1.406682e-11
numerical: -42.624425 analytic: -42.624425, relative error: 3.465745e-12오차가 거의 없는 것을 알 수 있다.
Inline Question 1
가끔 gradcheck의 차원이 정확하지 않을 수도 있다.
이러한 불일치의 원인은 무엇일까요? 우려할 만한 이유인가요? 그라데이션 체크가 실패할 수 있는 한 차원의 간단한 예는 무엇인가요? 이런 일이 발생하는 빈도에 따라 마진에 미치는 영향은 어떻게 달라질까요? 힌트: SVM 손실 함수는 엄밀히 말해 미분 가능하지 않습니다.
물어보는 것은 일단
1. numerical과 analytic의 차이가 왜 일어나는지
2. graident check가 실패할 경우, margin이 실패할 경우 어떤 영향이 일어나는지?
이다.
SVM loss function 은 max(0,x) 모양이다. x = 불일치 클래스 - 올바른 클래스 + 상수 이다. x가 0보다 크면 오차가 발생하고 0보다 작으면 0으로 설정한다.
일반적으로 x=0일 때 미분이 가능하지 않다. 이러한 경우가 gradient check에 실패한다.
만약 아주 0과 가까운 음수인 x = -1e-8이 있다고 하자. 그렇다면 max(0,x) = 0이기 때문에 analytic한 기울기는 0이다. 하지만 numerical 기울기는 다르다. 만약 h를 양수에서부터 오는 극한값이라 하자. (ex h = 1e-8) 그러면 max(0,x+h) = c > 0이기 때문이다. 그래서 numerical과 analytic의 차이가 있다.
x 값의 상수가 증가하면? 더 많은 x값들이 0보다 커질 것이다. 즉 손실점수가 더 커지고, 0인 값들이 없어지기 때문에 미분 불가능한 점들이 적어져서 gradient check 실패할 가능성이 적어진다.
svm_loss_vectorized
벡터화해서 다시 loss, dW를 구해보자.
np.maximum 함수에 대해서는 미리 공부하자.
연습문제로 다음 코드를 이해해보자.
W = np.array([ [1,2,3],[4,5,6],[7,8,9],[12,1,2],[13,4,2]])
print(W)
print()
arr = np.arange(5)
print(W[arr,1].reshape(5,1))[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[12 1 2]
[13 4 2]]
[[2]
[5]
[8]
[1]
[4]]이해가 되었다면 이제
code를 작성한다.
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
scores = X.dot(W)
correct_class_score = scores[np.arange(num_train), y].reshape(-1,1)
margin = np.maximum(0, scores - correct_class_score + 1)
#correct margin에 대해서 고려
margin[np.arange(num_train),y ] = 0
loss = margin.sum() / num_train
loss += reg * np.sum(W * W) scores는 내적하여 구한다.
correct_class_score는 arange를 통해서 0부터 499까지의 행의 올바른 값(y)에 접근하는 것이다. 그리고 하나의 행을 훈련 데이터 개수만큼의 행렬로 전치시킨다.
margin은 함수 그대로 사용할 수 있다. maximum 함수를 통해 한번에 여러 array에 접근이 가능하기 때문이다. 이때 j != yi 를 고려해야 하기 때문에 0을 더하고 모든 margin을 더한뒤 한번에 나눠준다.
그리고 regularization을 해주면 된다.
코드 작성 후 시간차이 비교이다.
Naive loss: 8.929866e+00 computed in 0.181815s
Vectorized loss: 8.929866e+00 computed in 0.004852s
difference: -0.000000속도 차이는 크고, 정확도의 차이는 거의 없다.
이제 미분값을 구해야하는데, 사실 이것도 만만치 않게 어려웠다.
아까 편미분 공식을 보면
정답 클래스일 때, 0보다 큰 것의 개수만큼 빼주는 것을 알 수 있다.
그리고 그 다음 x를 곱하는 것을 알 수 있다.
이 모든 것을 한번에 하는 코드는 다음과 같다.
margin[margin > 0] = 1
valid_count = margin.sum(axis = 1)
margin[np.arange(num_train),y ] -= valid_count
dW = (X.T).dot(margin) / num_train
dW += reg * 2 * W
일단 0보다 큰 것의 값을 1로 만든후 열로 더하면 각 행에서(각 훈련 케이스에서) 0보다 큰 개수들을 구할 수 있다.
np.arange를 통해 각 훈련 케이스의 정답 클래스 margin에서 개수들을 빼자. (두번째 공식 참고)
그럼 각 훈련케이스의 정답 클래스는 손실 개수만큼 -가 되는 것이다.
이미 margin은 0보다 큰것을 1로 설정했기에 j에 대한 추가적인 코드는 필요없고 바로 X를 내적하면 된다.
어렵다면 다음 코드를 먼저 이해하고 공부하면 좋을 것 같다.
W = np.array([ [1,0,3],[0,5,0],[0,8,0],[2,1,2],[13,0,1]])
print(W)
W[np.arange(5),1] = 0
W[W > 0] = 1
print(W)
print()
valid = W.sum(axis=1)
print(valid)
print()
W[np.arange(5),1] -= valid
print(W) t
[[ 1 0 3]
[ 0 5 0]
[ 0 8 0]
[ 2 1 2]
[13 0 1]]
[[1 0 1]
[0 0 0]
[0 0 0]
[1 0 1]
[1 0 1]]
[2 0 0 2 2]
[[ 1 -2 1]
[ 0 0 0]
[ 0 0 0]
[ 1 -2 1]
[ 1 -2 1]]미분의 차이도 속도 차이가 꽤 크고, 정확도의 차이는 없었다.
Naive loss and gradient: computed in 0.186250s
Vectorized loss and gradient: computed in 0.023591s
difference: 0.000000
LinearClassifier
train
지금까지 한게 뭐지? 바로 SVM 을 구현했다.
그러면 이제 선형분류기를 구현해서 SGD를 한번 해보자.
일단 근데 아직 LinearClassifier의 train 함수를 구현하지 않았다.
SGD를 통해 선형 분류기를 학습시켜보자.
일단 batch size 만큼 랜덤으로 선택해서 고른다.
예시 코드를 통해 이해해보자. 중복은 허용하지 않는다.
import random
res = [ 1,2, 3,4,4,3,431,1,2,2,222]
indices = np.random.choice(res,3, replace = False)
print(indices)[2 4 3]이렇게 작성하면 된다.
batch_indices = np.random.choice(num_train, batch_size, replace = False)
X_batch = X[batch_indices]
y_batch = y[batch_indices]그리고 이제 parameter를 update해야한다. 이는 공식에 따르면
new_W = old_W - learning_rate * gradients 이다.
self.W = self.W - learning_rate * grad
이렇게 작성한다.
train을 모두 구현 후
직접 실행하면
iteration 0 / 1500: loss 794.350099
iteration 100 / 1500: loss 290.218714
iteration 200 / 1500: loss 109.070153
iteration 300 / 1500: loss 42.860449
iteration 400 / 1500: loss 18.719957
iteration 500 / 1500: loss 10.458855
iteration 600 / 1500: loss 7.089050
iteration 700 / 1500: loss 6.282646
iteration 800 / 1500: loss 5.601564
iteration 900 / 1500: loss 5.160246
iteration 1000 / 1500: loss 5.571617
iteration 1100 / 1500: loss 5.493367
iteration 1200 / 1500: loss 5.588462
iteration 1300 / 1500: loss 5.859742
iteration 1400 / 1500: loss 5.278896
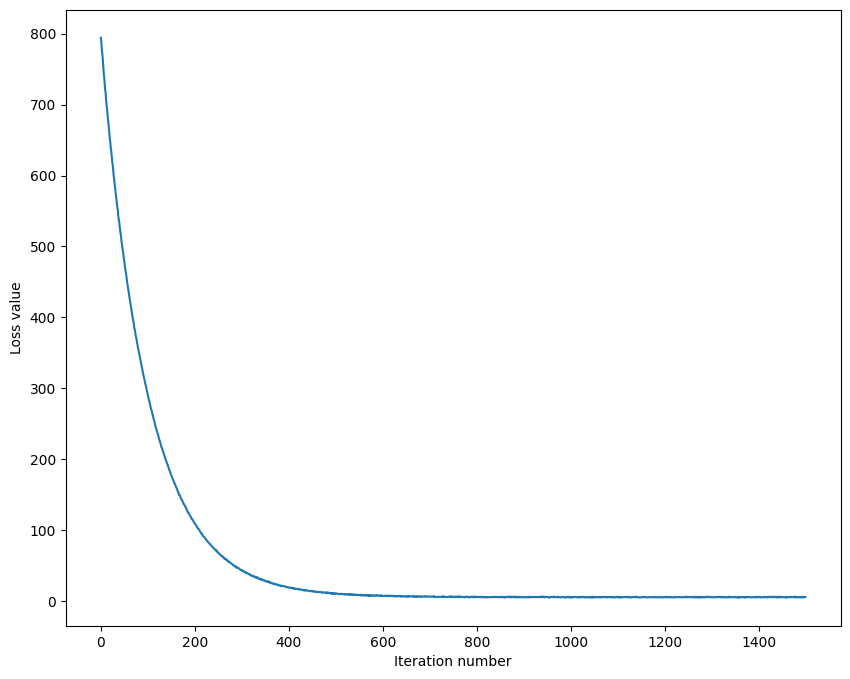
That took 15.212310sloss가 점점 줄어드는 것을 확인할 수 있다.
매번 실행시마다 값이 달라지는데, 이는 random으로 W가 초기에 선택되기 때문에 어느정도 값에 영향을 주는 것 같다. 또한 batch 도 랜덤이기 때문이다.
그래서 plot은 다음과 같이 보여준다.
그리고 예측 함수도 구현한다.
scores = X.dot(self.W)
y_pred = scores.argmax(axis = 1)
이건 Wx 값에서 클래스별 가장 큰 점수의 인덱스를 y_pred에 담는 것이다.
learning_rates = [1e-7, 5e-5]
regularization_strengths = [2.5e4, 5e4]이렇게 학습률과 정규화 강도를 설정해서, 총 4가지 조합에 대해 하이퍼파라미터를 실험해볼 예정이다.
for lr in learning_rates:
for rs in regularization_strengths:
svm = LinearSVM()
svm.train(X_train, y_train, lr, rs, num_iters = 500, verbose = True)
y_train_pred = svm.predict(X_train)
train_accuracy = np.mean(y_train == y_train_pred)
y_val_pred = svm.predict(X_val)
val_accuracy = np.mean(y_val == y_val_pred)
if val_accuracy > best_val:
best_val = val_accuracy
best_svm = svm
results[(lr,rs)] = (train_accuracy, val_accuracy)results 를 이렇게 저장해주면 된다.
실행결과
lr 1.000000e-07 reg 2.500000e+04 train accuracy: 0.364510 val accuracy: 0.370000
lr 1.000000e-07 reg 5.000000e+04 train accuracy: 0.351735 val accuracy: 0.371000
lr 5.000000e-05 reg 2.500000e+04 train accuracy: 0.053633 val accuracy: 0.049000
lr 5.000000e-05 reg 5.000000e+04 train accuracy: 0.070122 val accuracy: 0.068000
best validation accuracy achieved during cross-validation: 0.371000
가장 정확도가 높은 것은 첫번째 였다.
그리고 test 결과
linear SVM on raw pixels final test set accuracy: 0.358000정확도는 살짝 더 떨어졌다.
W 시각화

best w를 시각화했다. 각 class의 템플릿 형상을 보여준다.
Inline question 2
Describe what your visualized SVM weights look like, and offer a brief explanation for why they look the way they do.
그림을 보면 각각의 형상은 각 템플릿을 닮아있다. 다른건 모르겠지만 car, horse의 경우는 확실히 비슷하다.
이 이유는 무엇인가?
예를 들어 car class의 경우는 car와 곱해진 결과가 다른 데이터보다 곱해진 결과보다 더 값이 높도록 학습된다.
즉 real car image 의 픽셀과 W의 픽셀값은 비슷해진다. car의 픽셀값이 높은 곳에서 w의 픽셀값도 높고 car의 픽셀값이 낮은 곳에서 w의 픽셀값도 낮아질 것이다. 왜냐하면 곱해진 결과의 점수가 높아야하기 때문이다.
결과적으로 전체 픽셀의 분포가 표현해야하는 이미지의 모양과 비슷해질 수 밖에 없다.
