[231N] Assignment 1 - KNN

AND_E·2023년 11월 29일

과제

Stanford University CS231n, Spring 2017

목록 보기

4/10

과제1 를 시작한다.

과제는 Colab에서 수행하고, 일단 처음 환경설정하는 건 동영상을 보고 쉽게 따라할 수 있다.

과제 링크

그리고 과제 하나에 여러개의 과제가 또 있다.

순서대로

KNN
SVM
Softmax classifier
Two-Layer Neural Network
Higher Level Representations : Image Features

이다.

우선 KNN 과제를 수행해보겠다.

KNN

첫번째 과제는 KNN 과제이다. 2강에서 KNN에 대해 배웠다.
우리는 유클리디안 거리를 통해 KNN을 우선 구해보자.

compute_distances_two_loops 구현

일단은 첫번째로 모든 테스트와 훈련 데이터 예제의 거리를 구해야한다.
조잡하지만 2 loops를 통해 구현할 수 있다.

cs2231n > assignments > assignment1 > cs231n > classifiers 에 있는 k_nearest_neighbor.py 에서 코드를 수정하자.

이전 6번째 셀에서 우리는

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)

를 통해 class를 실행하고 훈련데이터를 저장했다.

compute_distances_two_loops의 parameter인 X는 테스트 데이터이다.

그리고 친절하게 함수에 써있듯 self.X_train 을 사용해서 각각의 훈련 데이터와의 거리를 구하자. 유클리디안 공식을 활용하면,

        for i in range(num_test):
            for j in range(num_train):
                #####################################################################
                # TODO:                                                             #
                # Compute the l2 distance between the ith test point and the jth    #
                # training point, and store the result in dists[i, j]. You should   #
                # not use a loop over dimension, nor use np.linalg.norm().          #
                #####################################################################
                # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

                dists[i][j] = np.sqrt(np.sum(np.square(X[i] - self.X_train[j])))

                # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        return dists

으로 작성할 수 있다.

# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()

이 셀을 실행하면

이 그림이 나온다.

결과적으로 500 * 5000 행렬 그림이고,
일반적으로 낮은 거리는 검정색, 높은 거리는 흰색으로 나타난다.

Inline question 1

What in the data is the cause behind the distinctly bright rows?
What causes the columns?

$\color{blue}{\textit Your Answer:}$ 만약 i번째 테스트 데이터가 train 데이터와 가깝다면 검정색으로 나타날 것이고 그 반대는 하얀색이다. 만약 j 번째 train 데이터가 테스트 데이터와 가깝다면 검정색으로 나타날 것이고 그 반대는 하얀색으로 나타날 것이다.

일단 이렇게 답했다.

k=1

k=1 일때의 knn은 가장 가까운 train을 선택하는 것이다.
이때 구현 전 실행한 결과 0.1의 정확도를 보였다.

Got 57 / 500 correct => accuracy: 0.114000

27% 의 정확도를 얻는것이 목적이라고 한다.
predict_labels를 수정해야한다.

일단 구현하기 위해서는 argsort, bincount, argmax 에 대해 알아야 한다.

링크를 통해 들어가서 공부했다.

첫번째 구현은 정렬 후에 k 번째 y train의 값들을 저장하는 것이다.

            closest_y = []
            #########################################################################
            # TODO:                                                                 #
            # Use the distance matrix to find the k nearest neighbors of the ith    #
            # testing point, and use self.y_train to find the labels of these       #
            # neighbors. Store these labels in closest_y.                           #
            # Hint: Look up the function numpy.argsort.                             #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            s = dists[i].argsort() 
            closest_y = self.y_train[s[:k]]

정렬 후 closest_y에 저장한다.

그 다음 closest_y의 라벨 값들의 개수를 모두 bincount로 센 다음, 가장 많은 값을 가진 인덱스를 argmax로 추출한다.

y_pred[i] = np.argmax(np.bincount(closest_y))

Got 139 / 500 correct => accuracy: 0.278000

이때 정확도는 약 27%이고
그럼 k=5로 설정했을 때 정확도는 아주 조금 커진 것을 알 수 있었다.

Inline question 2

We can also use other distance metrics such as L1 distance.
For pixel values $p_{ij}^{(k)}$ at location $(i,j)$ of some image $I_k$ ,

the mean $\mu$ across all pixels over all images is $\mu=\frac{1}{nhw}\sum_{k=1}^n\sum_{i=1}^{h}\sum_{j=1}^{w}p_{ij}^{(k)}$
And the pixel-wise mean $\mu_{ij}$ across all images is
$\mu_{ij}=\frac{1}{n}\sum_{k=1}^np_{ij}^{(k)}.$
The general standard deviation $\sigma$ and pixel-wise standard deviation $\sigma_{ij}$ is defined similarly.

다음 중 L1 거리를 사용하는 가장 가까운 이웃 분류기의 성능을 변경하지 않는 전처리 단계는 어느 것입니까? 해당하는 항목을 모두 선택하세요. 명확히 하기 위해, 훈련 예와 테스트 예는 모두 같은 방식으로 전처리됩니다.

Subtracting the mean $\mu$ ( $\tilde{p}_{ij}^{(k)}=p_{ij}^{(k)}-\mu$ .)
Subtracting the per pixel mean $\mu_{ij}$ ( $\tilde{p}_{ij}^{(k)}=p_{ij}^{(k)}-\mu_{ij}$ .)
Subtracting the mean $\mu$ and dividing by the standard deviation $\sigma$ .
Subtracting the pixel-wise mean $\mu_{ij}$ and dividing by the pixel-wise standard deviation $\sigma_{ij}$ .
Rotating the coordinate axes of the data, which means rotating all the images by the same angle. Empty regions in the image caused by rotation are padded with a same pixel value and no interpolation is performed.

$\color{blue}{\textit Your Answer:}$
1.2.

$\color{blue}{\textit Your Explanation:}$

일단 1,2를 맞다고 생각하는데 1,3이 맞다고 생각하는 사람들도 많았다.
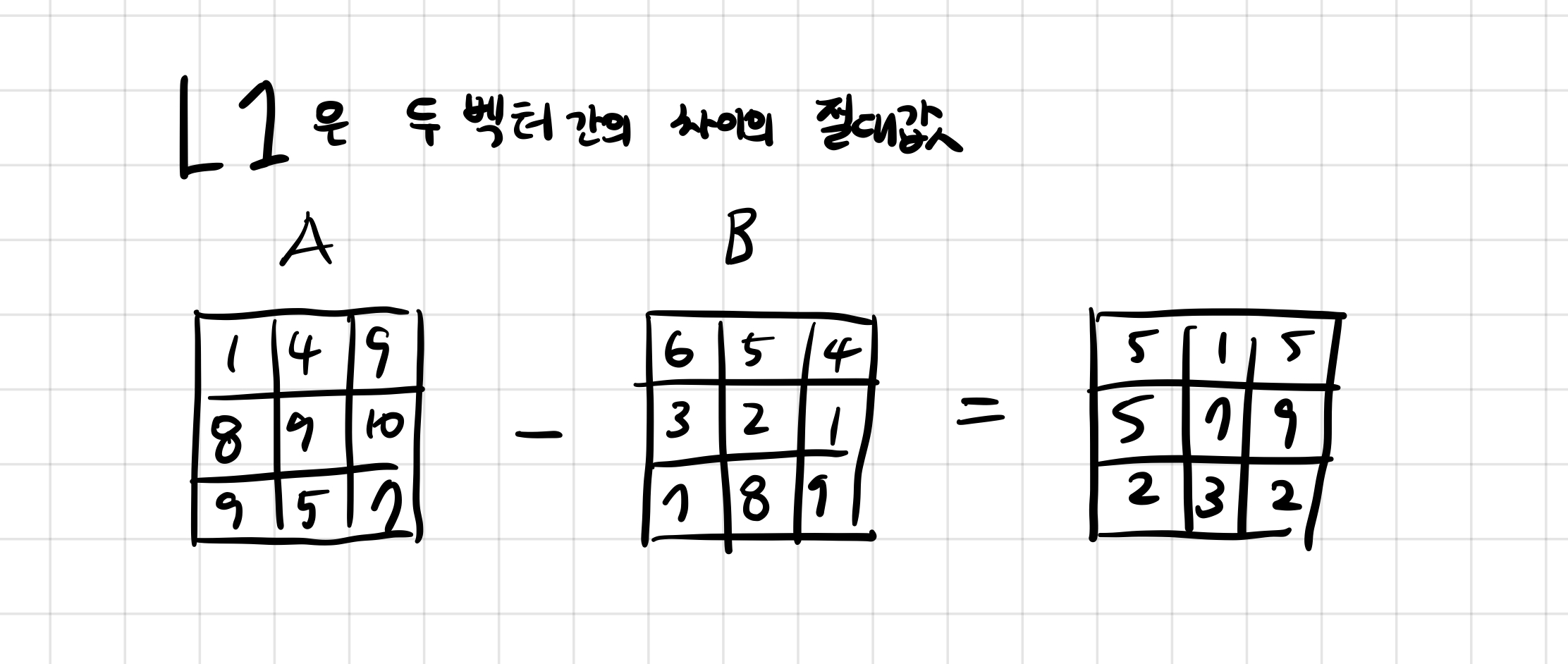
L1은 이미지 a, 이미지 b가 있다면 각 i,j 위치의 픽셀에서 차이의 절대값을 의미한다.
그래서 일단 어떤 식으로 변경을 하던, 이 전처리를 수행하기 전과 후의 값이 절대로 바뀌면 안된다고 생각한다. 그래서 바뀐다면 성능이 바뀌는 것이라 생각한다.

그래서 일단 1번은 모두 같은 값 u로 빼는 것이기 때문에 차이는 동일하다. 그래서 1번은 성능을 변경하지 않는다.
2번은 각 픽셀의 평균값으로 빼는 것이다. 이것도 성능의 차이는 없다고 생각한다. 왜냐하면 각 픽셀의 위치에 따른 평균값을 빼는 것이고 이는 결국 차이가 동일하다.

예를 들어 A의 0,0 번째 픽셀이 있다고 하고 0,0위치의 픽셀 평균은 $\mu_{00}$ 이라고 할때,
$|(p_{00}^{(a)} -\mu_{00}) - (p_{00}^{(b)} -\mu_{00})| = |p_{00}^{(a)}- p_{00}^{(b)}|$ 이다.

3번의 경우 평균을 빼고 표준 편차로 나누는 것인데 이는 표준 편차로 나눔으로써 값이 변하게 된다.
4번 또한 표준 편차로 나누기 때문에 값이 변경되고 결과적으로 성능에 차이가 있다고 생각한다.
5번의 경우에는 회전을 해도 되는가를 물어본다.
90도씩 변경되는 경우는 값이 차이가 없지만 45도씩 변경되는 경우 빈공간이 발생하고 이는 동일한 픽셀값으로 바뀐다고 해도 이전의 픽셀값과의 차이가 있다고 생각하여 성능 차이가 있다고 생각한다. L2의 경우에는 거리가 원 모양이지만 L1의 경우는 거리가 마름모 꼴이다. (2강 참조)

compute_distances_one_loop 구현

이전에는 two loops를 구현했다면 이제는 one loop을 구현해보자.

i번째 test data와 동시에 모든 train data를 비교하는 것이다.

여기서는 sum axis 개념이 쓰인다.

dists[i, :] = np.sqrt(np.sum(np.square(X[i] - self.X_train), axis = 1))
이렇게 구현했고 다음은 루프 없이 구현해보자.

compute_distances_no_loops

이거 꽤 오래걸렸다ㅠㅠ 에휴

        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        #(a-b)^2 = a^2 + b^2 - 2ab
        A = np.sum(X**2, axis = 1).reshape(-1,1)
        B = np.sum(self.X_train**2, axis = 1)
        C = 2 * np.matmul(X, self.X_train.T)
        dists = A + B - C
        dists = np.sqrt(dists)
        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

시작은 test data와 train data 행렬을 전체 큰 행렬로 보는 것부터 시작한다.
이 둘을 A,B라고 하면 (A-B)(A-B) = A^2 + B^2 - 2AB 로 풀어나갈 수 있다.
작은 예시를 통해 이 코드를 이해해보자.

import numpy as np
arr = np.array([[1,1,2],[1,3,3]])
arr2 = np.array([[1,2,3],[1,2,3],[1,2,3]])

arr = np.sum(arr**2, axis = 1).reshape(-1,1)
arr2 = np.sum(arr2**2, axis = 1)
print(arr)
print(arr2)
result = arr+arr2
print(result)
print(result.shape)

output:

[[ 6]
 [19]]
[14 14 14]
[[20 20 20]
 [33 33 33]]
(2, 3)

결과를 보면 일단 첫번째 배열은 제곱이 된 후 행으로 나타나고, 두번째 배열은 제곱이 된 후 열로 나타난다.
이를 더한 것은 각각 행과 열에 더한 값이 나온다. 모양은 (2,3)임을 알 수 있다.

A = np.sum(X**2, axis = 1).reshape(-1,1)이 부분이 이제 A^2인데, 자기자신을 곱하고 (-1,1)로 변형하면 (500,1) 모양이 된다.

B^2 부분이 B = np.sum(self.X_train**2, axis = 1) 인데 이제 제곱을 한 뒤 모양은 (5000,) 이다. 5000개의 열이라고 생각할 수 있다.

즉 둘을 더하면 (500,5000)이 되고 C는 A,B 행렬을 곱한 것이기 때문에 (500,5000)의 모양을 갖는다.

모두 더한 뒤 sqrt를 구할 수 있다.

속도비교

Two loop version took 38.010734 seconds
One loop version took 51.271788 seconds
No loop version took 1.017225 seconds

No loop 가 훨씬 빠른 것을 알 수 있다.

k-fold

새로운 걸 이번에 많이 배운는데, k-fold를 하기 위해서는 나누는 것이 필요하다.
이를 numpy array_split 을 통해 할 수 있다.

그냥 split과 array_split의 차이는 split은 딱 나눠지지 않으면 error를 출력하지만, array_split은 error를 출력하지 않는다.
그래서 array_split을 사용하여 작성할 수 있다.

# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

그리고 구현한 k-fold를 통해 knn의 최적 k를 구해보자.

# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
  k_to_accuracies[k] = []
  for i in range(num_folds):
    X_train_fold = np.concatenate([ fold for j, fold in enumerate(X_train_folds) if i != j ])
    y_train_fold = np.concatenate([ fold for j, fold in enumerate(y_train_folds) if i != j ])
    
    classifier.train(X_train_fold, y_train_fold)
    y_pred_fold = classifier.predict(X_train_folds[i], k=k, num_loops = 0)


    num_correct = np.sum(y_pred_fold == y_train_folds[i])
    accuracy = float(num_correct) / num_test
    k_to_accuracies[k].append(accuracy)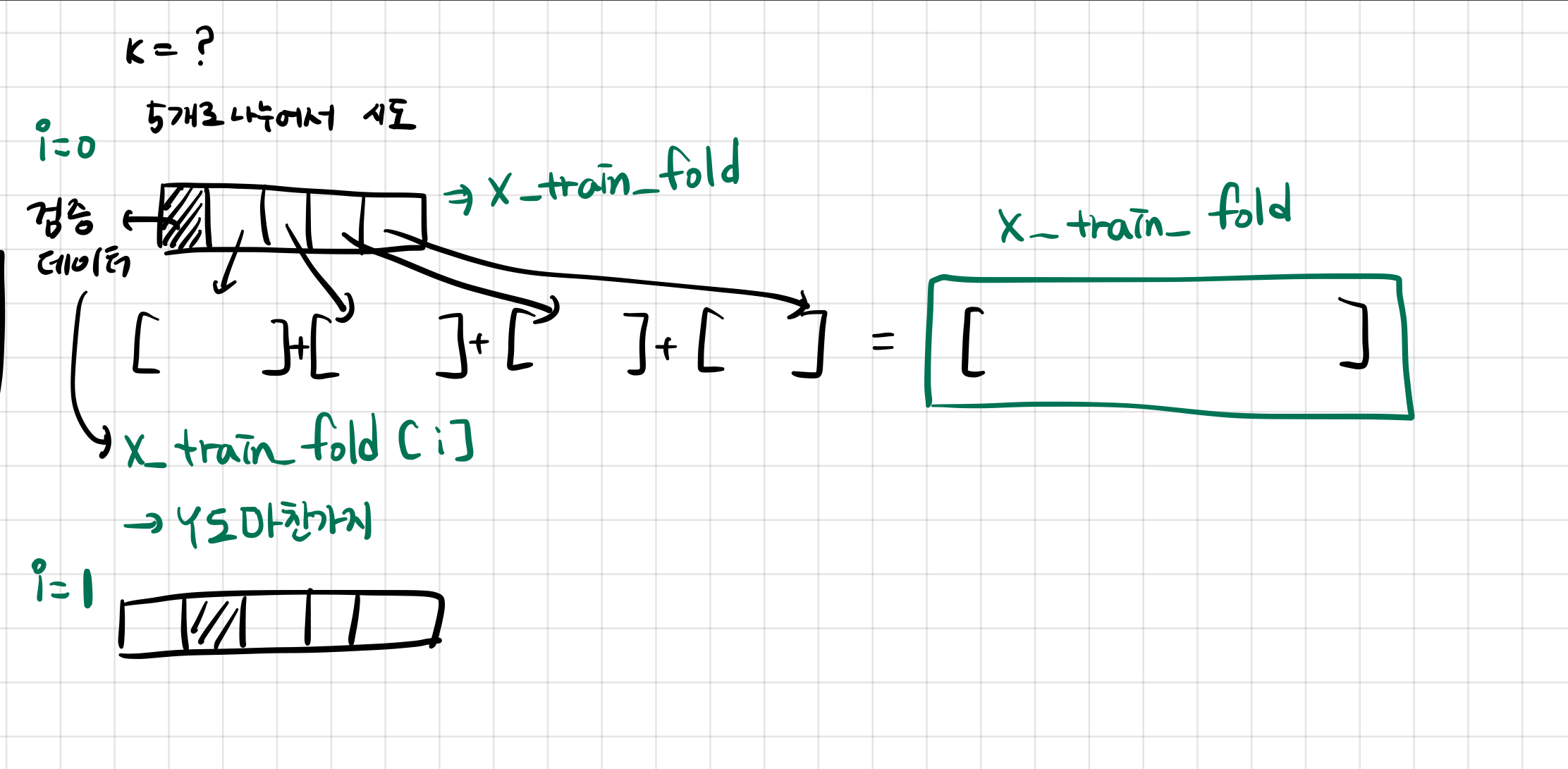

그리고 그래프를 출력하면,

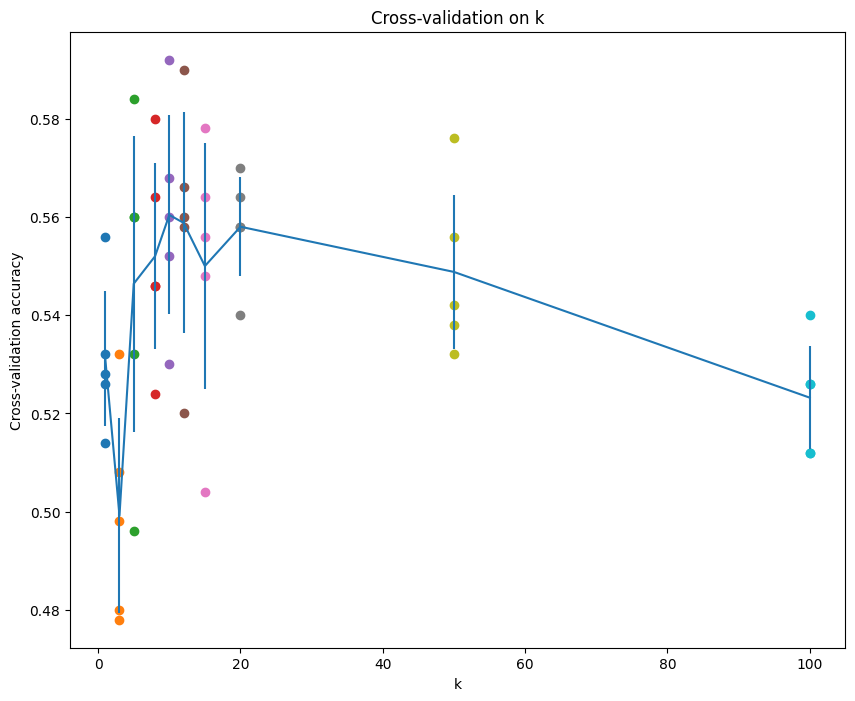
이런 그래프가 출력되고 best한 k를 찾아보자.
일단 가장 높은 값인 k=10을 선택하면,
Got 141 / 500 correct => accuracy: 0.282000
k=12
Got 128 / 500 correct => accuracy: 0.256000
k=20
Got 136 / 500 correct => accuracy: 0.272000

보니 가장 좋은 건 10일때이다.

Inline Question 3

Which of the following statements about $k$ -Nearest Neighbor ( $k$ -NN) are true in a classification setting, and for all $k$ ? Select all that apply.
1. The decision boundary of the k-NN classifier is linear.
2. The training error of a 1-NN will always be lower than or equal to that of 5-NN.
3. The test error of a 1-NN will always be lower than that of a 5-NN.
4. The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
5. None of the above.

$\color{blue}{\textit Your Answer:}$

2.4

$\color{blue}{\textit Your Explanation:}$

x. 경계는 일직선 모양인가? 아니다. 들쑥날쑥할 수 있다.
o. 훈련데이터에 대해서 k=1일때보다 k=5일때 항상 오류가 적을까? 에대한 질문이다. 이는 훈련데이터에 대해서는 자기자신을 고를 수 밖에 없기 때문에 k=1이 더 오류가 적다.
x. 아까 20보다 10을 선택한 것이 더 정확도가 높은 것처럼 항상 그런 것은 아닐 것이다.
o. 훈련데이터가 많아질 수록 당연히 분류시간은 더 많아진다. 왜냐하면 계산량이 늘어나기 때문이다.