Lecture 7

모델을 train 시키기 위해 필요한 개념 2를 정리하도록 한다.

강의링크

이번 강의에서는

• Fancier optimization
• Regularization
• Transfer Learning

에 대해 알아보자.

Optimization (최적화)

기존의 최적화는 vanilla gradient descent 로 기울기를 계산하고, 학습률과 기울기를 곱해서 기존 weights에서 뺀다.

근데 기존 바닐라 최적화 방법은 문제가 있다.

만약 손실이 한 방향에서 빠르게 나타나고 다른 방향에서는 느리게 나타나게 되면 어떻게 되는가?

만약 타원형의 좌표가 있고, 빨간 점에서 웃음점(최적점)으로 이동을 해야한다고 하자.
이때, x축(수평) 방향의 loss는 느리고, y축(수직) 방향의 loss는 빠르다고 가정하자.
그렇게 된다면 항상 y축 방향으로만 다음 위치를 선정할 것이다.

이렇게 된다면 지그재그 모양으로 길이 나타나고 결국 비효율적이게 되는 것이다.

또 다른 문제도 있다.

loss function이 local minima 또는 안장점이 있다면?

만약 극소값이 있다면, 지역극소값은 전체 함수의 최소값을 보장하지 않기 때문에
해당 점보다 더 낮은 극소값이 있는지 확인해야하지만, 바닐라 최적화 방법에서는 LOSS가 0이되면 해당 점을 최소로 보고 다음 점을 찾지 않는다.

또한 안장점에서는 기울기가 모든 방향에서 느리게 작동하기 때문에 학습 속도가 너무 느려진다는 단점이 있다.

그리고 보통 차원이 작다면 local minima가 문제가 되지만 보통의 차원은 엄청 많고, 이때는 local 보다는 안장점문제가 더 많아지게 된다. 모든 차원에서 오목 들어가는 형태(local minima)는 거의 없기 때문이다.

그래서 이를 보완한 방법이 하나 있다.

SGD + Momentum

기존 코드에서 vs라는 속도를 추가한다.

Velocity는 기울기의 평균이라 볼 수 있고 Rho는 friction이다. (마찰력)
약간 물리적으로 접근한 것이라 볼 수 있다.

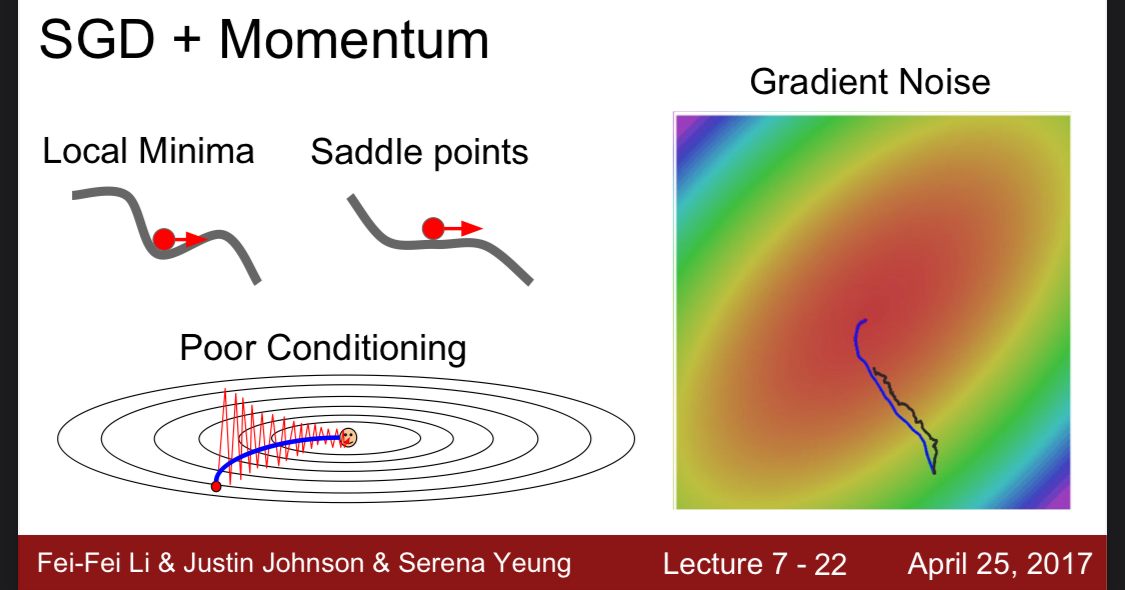
그래서 기존 바닐라 최적화에서 local minima와 saddle point에서 고여있던 점들이 속도를 추가하면 그 점을 빠져나와 다음 점을 찾는 것이다.

Nesterov Momentum

Nesterov는 기존 Momentum을 추가한 방법에서 조금 더 나아간 방법이다.

현재 위치에서 모멘텀을 추가한 방법과 다르게 모멘텀으로 인한 예측된 다음 위치에서 그래디언트를 계산한다.
이렇게 계산하면 모멘텀방향으로 더 정확한 그래디언트를 계산할 수 있다고 한다.

즉 모멘텀 방향으로 미리 약간 이동한 지점에서의 기울기를 찾는것이다.

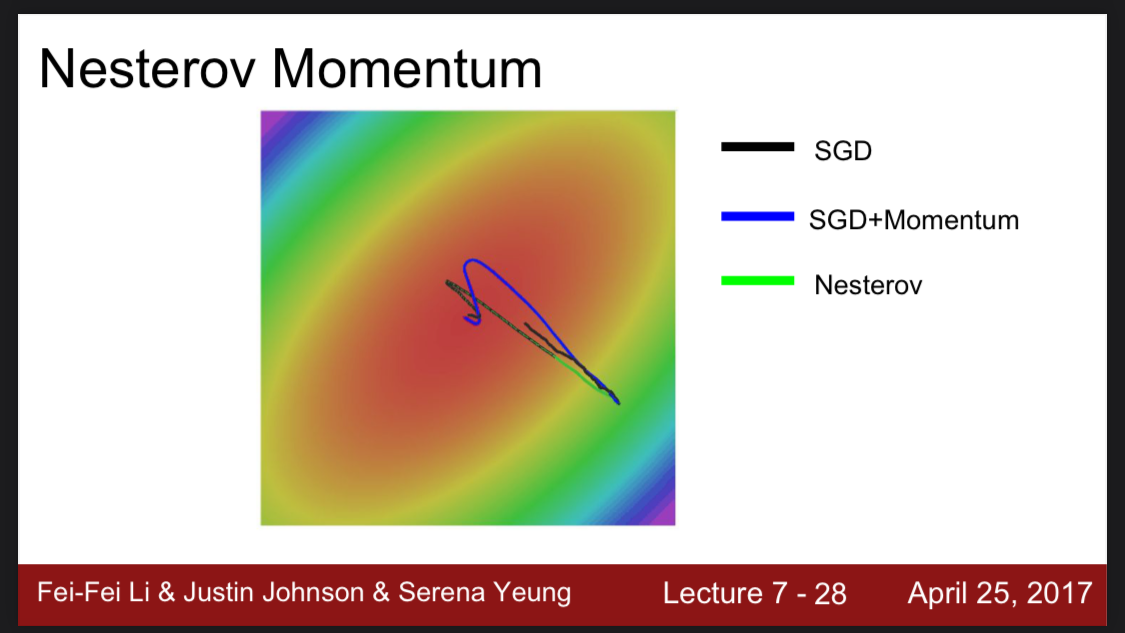
비교하면 그냥 모멘텀을 사용한 선보다 덜 오버슈팅이 된 것을 확인할 수 있다.

여기서 질문.
만약 속도때문에 지나치는 최솟값이 있는 경우는 어떻게 처리하는가?

날카로운 최솟값이 있다면, 사실 그 값은 별로 좋지 못한 값일 수도 있다. 이 말은 너무 훈련 데이터에 최적화되어 있어서 과적합이 일어난 최소값이라는 의미이다. 좋은 최소값은 날카롭게 아래로 그려진 그래프가 아닌 완만하게 오목한 그래프이다.

AdaGrad

또 다른 최적화 방법이다.

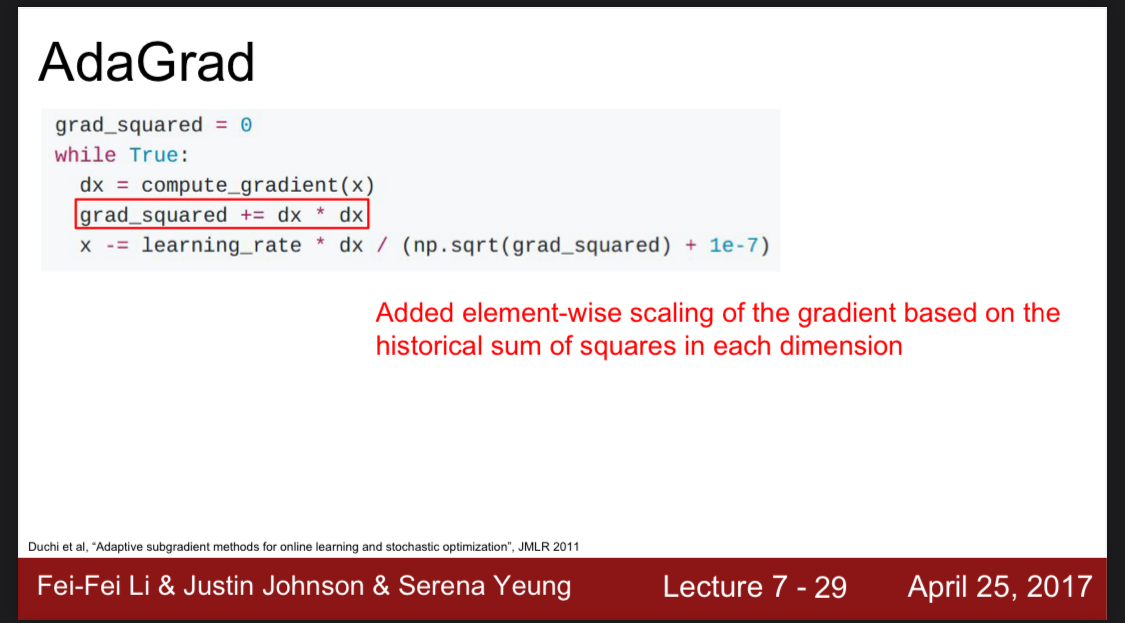
이 방법은 훈련 기간 동안 나타난 모든 그라디언트의 제곱을 누적해서 더하는 것이다.

그렇게 된다면 점점 단계가 진행될 수록 그라디언트의 제곱을 더하게 되고 그다음 제곱근으로 나누게 되니 학습률은 점점 줄어들게 된다.

이는 볼록구조를 가진 형태에 유용하다. 볼록구조는 점점 학습률이 줄어드는 구조가 적합하기 때문이다.

하지만 볼록구조가 아니라면 수렴하는데 너무 시간이 오래 걸리기 때문에 적합하지 않다. 이를 수정한 다른 최적화 방법이있다.

RMSprop

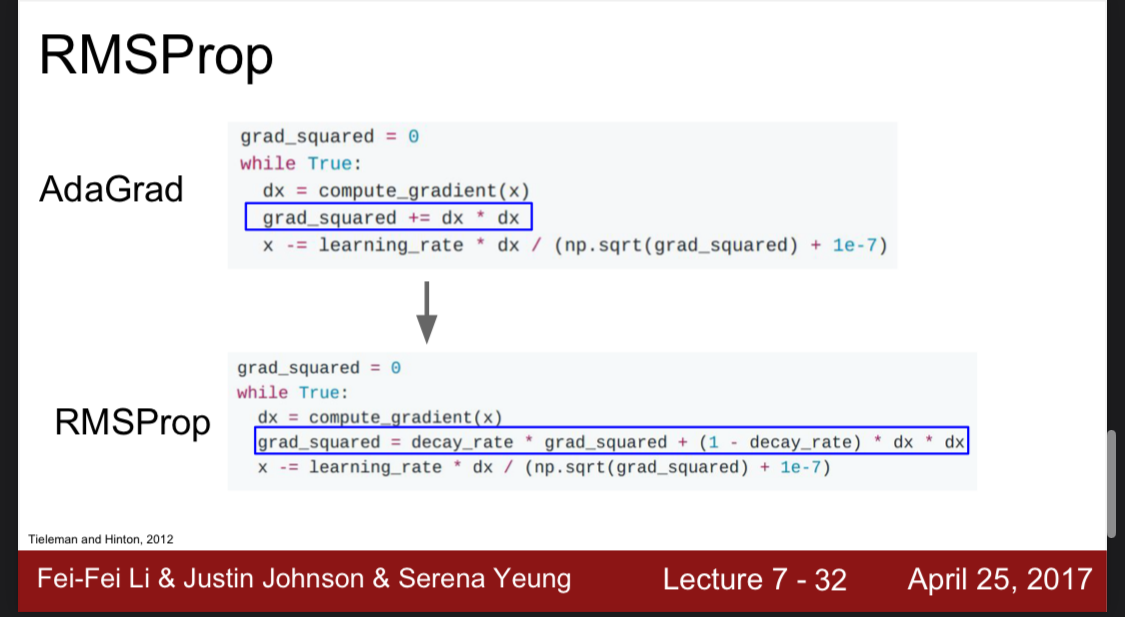
RMSprop은 부식정도(decay rate)를 통해 어느정도 이전 그래디언트를 삭제하고 나머지를 더하는 구조로 AdaGrad를 보완했다.

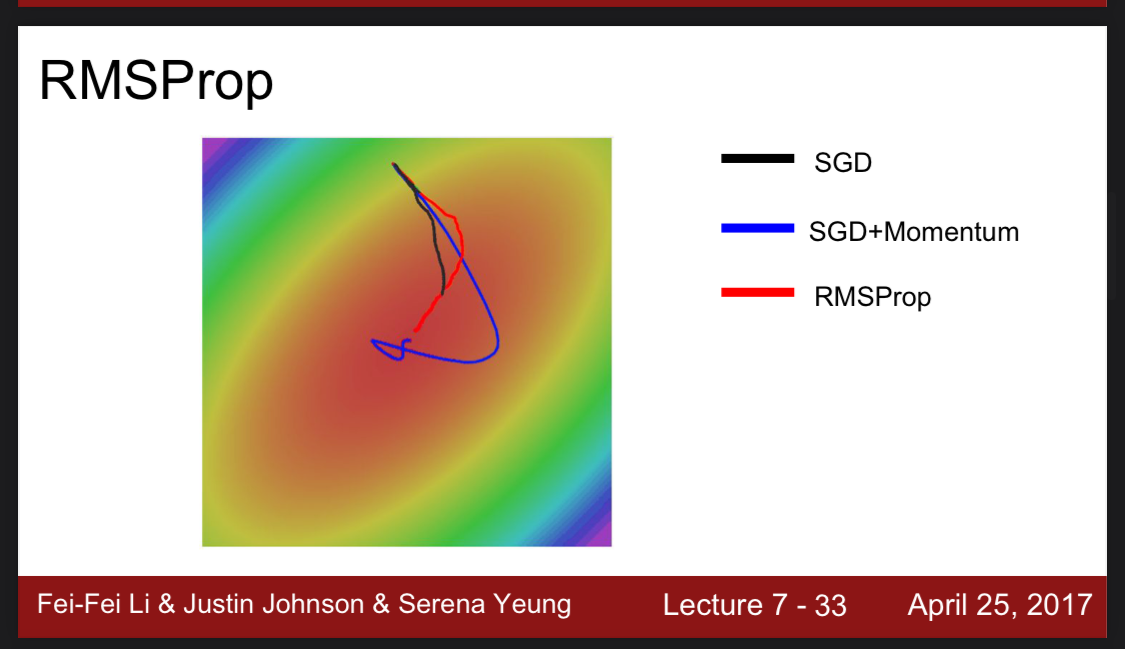
그림을 보면 RMSprop은 모멘텀을 추가한 SGD보다 오버슈팅이 없고 SGD보다는 빠르게 최적점에 도달한 것을 확인할 수 있다.

Adam

Adam 최적화 기법은 Momentum과 RMSprop의 최적화 방법을 섞은 것이라 볼 수 있다.

첫번째 first_moment의 경우는 Momentum을 다루었고, second_moment는 RMSprop을 다룬 것이다.
보통의 beta1은 0.9로 설정한다고 한다.
맨 처음 시행을 보면,
first_moment = 0.9 x 0 + (1 - 0.9) x dx = 0.1 x dx 임을 알 수 있다.
beta2는 보통 0.999로 설정한다고 한다.
second_moment = 0.999 x 0 + (1 - 0.999) x dx = 0.001 x dx 이다.

근데 이렇게 된다면, 처음부터 아주 작은 값(0에 근사한 값)으로 학습률을 시작하기 때문에 약간의 편향을 조정한다.

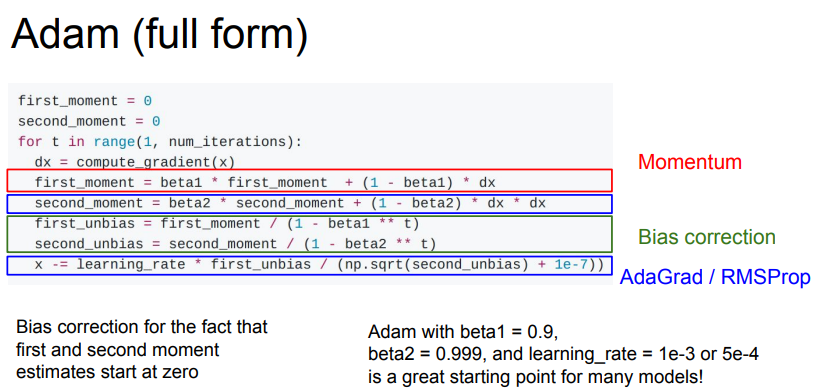
이렇게 작성한다면 t는 t단계를 의미한다. 따라서 t가 커질수록 beta는 1보다 작기 때문에 beta1 ^t는 점점 작은 숫자가 되고, 1-beta1^2는 점점 더 커진다. 분모에 있기 때문에 first_unbias는 점점 더 작아지는 것이다.

이는 점점 학습률을 줄여야하는 목표와 일치한 것을 알 수 있다.

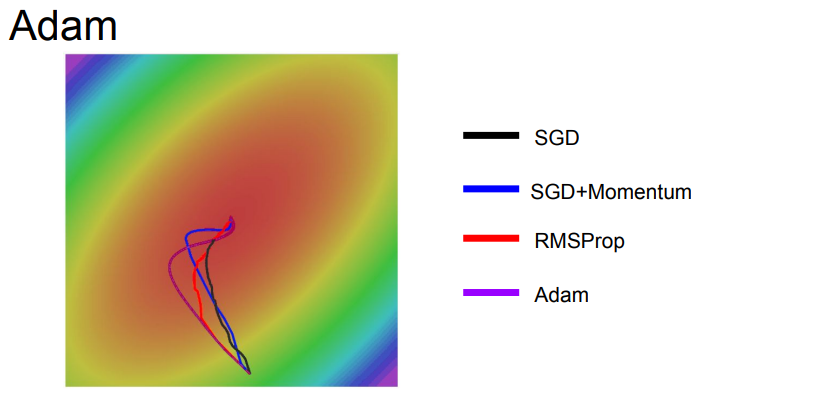
Adam의 선은 모멘텀의 선보다 덜 오버슈팅되지만 다른 선들에 비해 깔끔한 것을 알 수 있다.

hyperparameter learning rate

learning rate는 훈련때마다 항상 같은 비율을 유지하지 않는다.

좋은 learning rate는 초기는 크게 잡고 점점 비율을 줄여나가는 것이다.

이는 여러 방법이 있다.

• step decay
  - few epochs를 거치고 반으로 비율을 줄이는 것이다.
• exponential decay
  - $\alpha = \alpha_0 e^{-kt}$
• 1/t decay
  - $\alpha = \alpha_0 / (1+kt)$
  

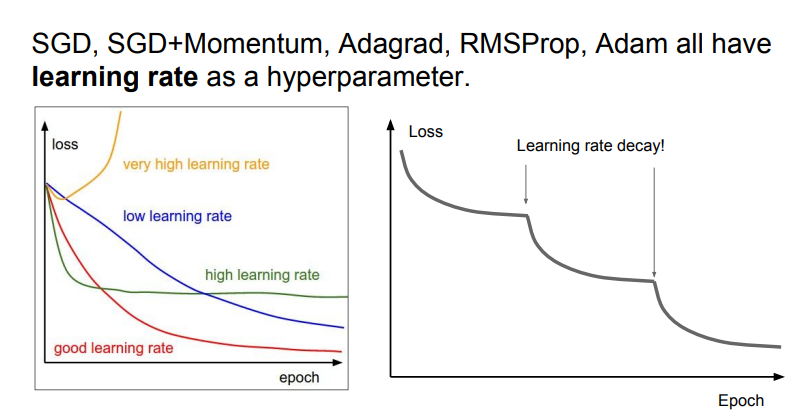
위 그래프를 보면 어느정도 진행이 되고 급진적으로 loss가 떨어진 곳이 있다. 이 부분이 바로decay가 이뤄진 곳이다. 이 경우는 step decay가 일어난 것이다.

Second - Order Optimization

지금까지 그래디언트를 계산할 때 테일러 1차 근사법인 first-order optimization을 사용했다.

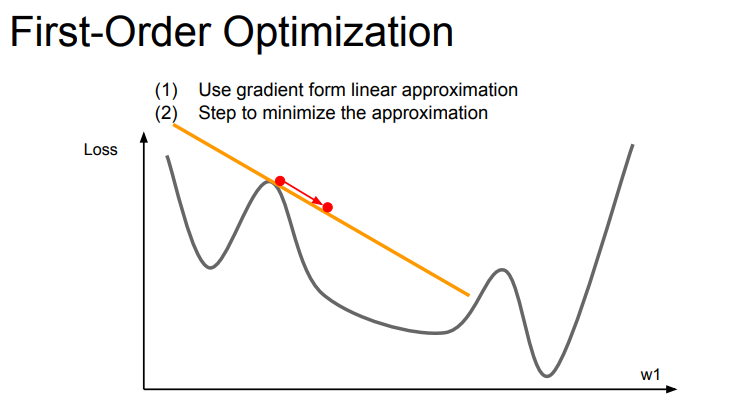
이 경우는 빨간점에 현재 위치해 있을 때 직선 아래로 이동하게 된다.

하지만 2차 최적화는 1차 도함수와 2차 도함수를 모두 고려한 근사법이다. 2차 테일러 근사법을 만들어 이차식을 사용해서 함수를 극소적으로 만든다.

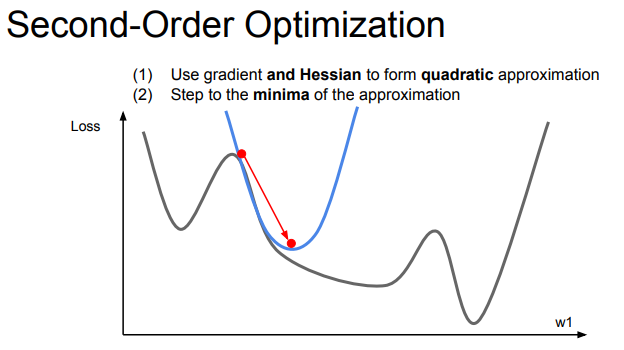
이렇게 1차 근사식을 사용한 것보다 더 빠르게 다음 점을 찾을 수 있다.

이 방법을 사용하면 뭐가 좋을까?

바로 학습률을 고려하지 않아도 된다는 점이다.

하지만 뭐가 안좋을까?

2차 미분값은 Hessian Matrix가 필요하고

단점은 전치를 시켜야하기 때문에 nxn 크기의 계산이 필요하고 이는 n이 커질수록 비용과 시간이 커진다.

• 시간 복잡도는 O(n^3), 공간 복잡도는 O(n^2)

BGFS, L-BGFS 방법도 있다는데 이건 간단하게 넘어간다.

---

Model Ensembles

지금까지는 사실 train error 를 줄이는 것을 목표로 두었지만 가장 중요한 것은 train error와 test error의 간극을 좁히는 것이다.

그러한 간극을 좁히기 위한 방법 중 하나는 앙상블이다.

모델 앙상블은 여러개의 독립적인 모델을 합해서 하나의 예측을 수행하는 기법이다.

1. 여러개의 독립적인 모델들을 train한다.
2. test time 때 그들의 결과들을 평균낸다.

하는 방법으로 진행된다.

Tips and Tricks

조금 더 창의적인 방법이 있다.

독립적인 모델들을 훈련하는 대신 여러 스냅샷들을 모델 훈련중에 사용하는 것이다.

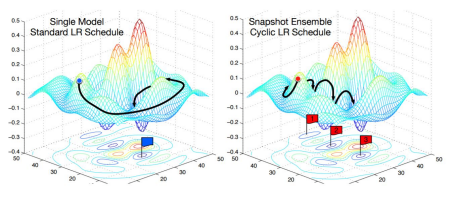
내가 이해한 바로는 독립적인 모델들을 각자 따로 만드는 것이 아니라 하나의 모델 중에서 스냅샷들을 저장하고 test시 스냅샷을 사용하는 것이다.

단점은 하나의 모델을 여러번 학습시켜야하기 때문에 굉장히 시간이 오래 걸린다는 점이다.

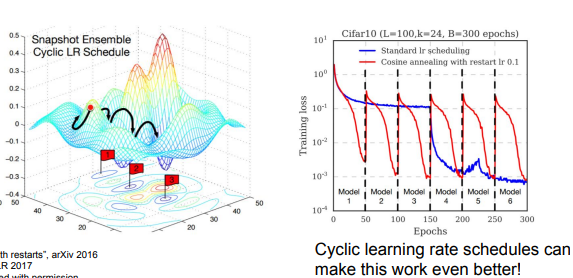
learning rate를 변화시켜서 더 좋은 loss 값을 찾을 수 있다. 점진적으로 learning rate를 감소시킨 다음 다시 일정 Epochs가 지나면 증가시키는 방법이다. 이 방법은 한번의 train으로 다양한 손실 지역에 수렴할 수 있기에 효과가 좋다.

Regularization

어떻게 single - model perfomance를 증가시킬 수 있을까?

Regularization을 통해 가능하다.

우리는 이미 Regularization을 배웠다. L1, L2 정규화이다.

좀 더 Fanicer 한 것에 대해 배워보자.

Dropout

이름부터 바로 알 수 있다시피 뭔가를 Drop (빼고) Out (제외시킨다) 이다.

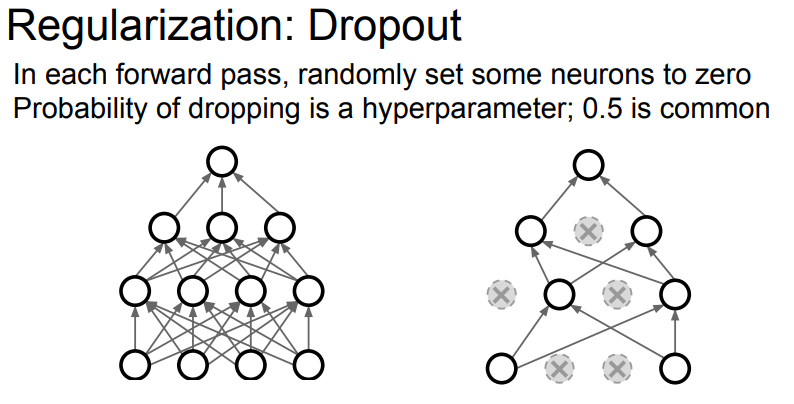
그림을 보면 쉽게 이해할 수 있는데,

뉴런 자체를 0으로 꺼버리는 것이다. 한 layer에서 랜덤으로 어떤 뉴런을 활성화에서 제외할 지 선택하고 그 다음 layer로 이동한다.

p를 0.5로 설정했기 때문에 H1의 값들이 만약 0.5보다 작게되면 0, 아니면 1로 설정해서 꺼버리는 것이다. 따라서 p값이 커지면 덜 꺼지고 작아지면 더 많이 꺼지게 된더,

Dropout이 왜 좋은 방법일까?

학습하면서 사실 모든 뉴런을 공평하게 보면서 학습하지 않을 것이다. 더 점수가 잘나오게 하기 위해서 어떤 뉴런에 더 의지를 할 수 있다. Dropout은 이렇게 과도하게 하나의 feature에 더 의존하는 현상을 방지한다.

결과적으로는 과적합을 방지한다고 한다.

다른 관점에서는 여러 앙상블을 학습시키는 것으로 볼 수 있다.

왜냐하면 각 layer 마다 다른 뉴런을 선택한다. 랜덤으로. 따라서 forward마다 다른 모델을 만드는 것과 동일하다.

그래서 Dropout은 동시에 거대 앙상블 모델을 학습시키는 것과 동일하다.

그럼 이렇게 학습을 했다고 하면 어떻게 test 할까?

$y = f_W(x,z)$
y는 output 이고 x는 input이고 z는 random mask 이다.

그래서 이를 평균내는 방법은 위 공식을 적분하는 것이다.

$\int{p(z)f(x,z)}$

근데 미분보다 사실 적분이 더 어렵다.

그럼 더 계산하기 쉽게 확률적으로 접근해보자.

만약 2개의 뉴런이 있고 그 다음 layer에 a가 있다고 하자. 그러면 w1, w2는 가중치이고 x,y가 꺼지거나 켜질 경우의 수는 4개이다. 이것들을 모두 계산해서 평균을 내자.
결과적으로 2개일 때는 $1/2(w_1x + w_2y)$이다.

그럼 이렇게 된다면 p = 0.5이고 항상 테스트 때마다 0.5를 곱해줘야 한다.

시간을 더 절약할 수 없을 까?

훈련할 때 그냥 바로 p를 나눠주는 것이다.

test가 좀 더 간단해졌다.

Dropout을 사용하면 좀 더 학습시간이 길어지지만 좋은 일반화 모델을 얻을 수 있게 된다.

• 학습시에는 Random을 추가해서 train data에 overfitting 하지 않게 만든다.
• 테스트시에는 randomness를 평균화하여 계산한다.

Mini-batch 를 사용해서 Regularization 하는 방법도 있다. 바로 Batch-Nomalization인데 이는 지금 자세히 다루지는 않겠다.

정리하면 Dropout을 사용하면 어떤 뉴런에 대해 의존하는 현상을 줄이는 것이고, 이는 노이즈를 추가해서 조금 더 일반화 시키는 방법이라고 할 수 있다.

Data Augmentation

Data Augmentation는 데이터에 대해서 Regularization을 시키는 것이다.

그러니까 만약에 고양이 사진이 있다면, 고양이 사진을 반대로 뒤집거나 사진의 명암도를 조절하거나 하는 등의 변형을 주는 것이다. 이전 사진을 변형을 시켜도 사실 고양이가 사자가 되지 않는다.
고양이 사진은 고양이 사진이 유지된다.

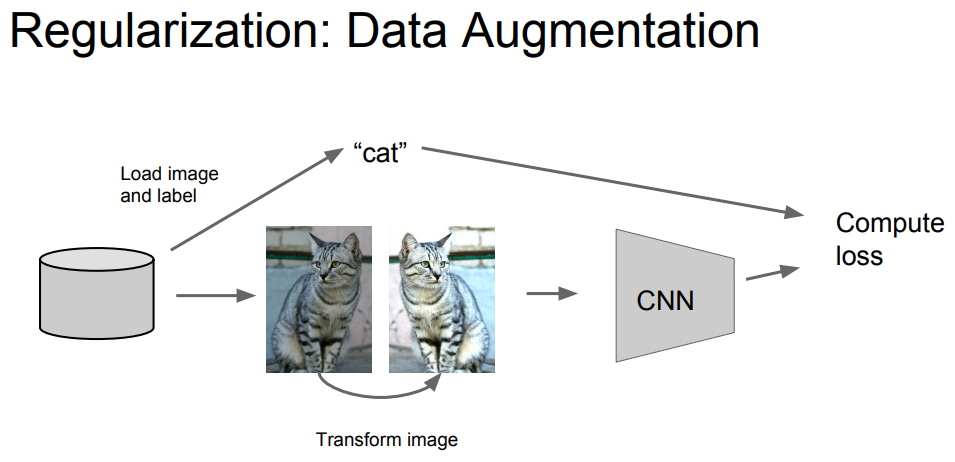
이미지 사진을 크롭하거나 크기를 바꿔서 학습을 시키기도 한다.

그리고 test할 때는 크기를 여러개로 하고 각각의 크기에 대해 크롭을 해서 test를 진행한다.

Data Augmentation에는 다양한 방법이 있다.

• translation
• rotation
• stretching
• shearing,
• lens distortions

DropConnect

아까 Dropout은 뉴런을 선택하지 않는 것이라면 이 DropConnect는 weight를 임의로 0으로 만들어버리는 것이다.

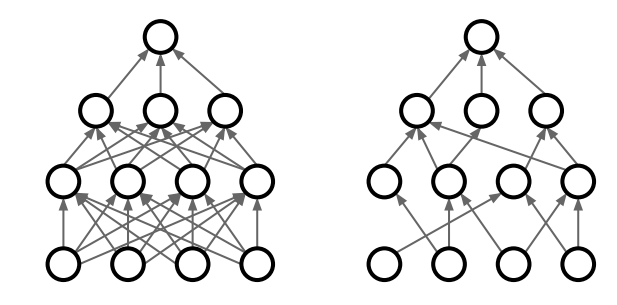
Fractional Max Pooling

잘 쓰지 않는 방법인데 꽤나 좋은 방법이라고 한다.

기존의 Max Pooling 은 고정된 지역에 대해서 진행했지만 여기서는 임의로 선택된 지역에 대해서 Max Pooling을 진행한다.

test 할 때는 pooling 할 지역을 고정하거나 여러개의 pooling 지역을 평균하는 방법이 있다고 한다.
사실 잘 이해가 되지 않았다 이건

Stochastic Depth

이 방법은 layer를 임의로 선택하여 학습하는 방법이다.

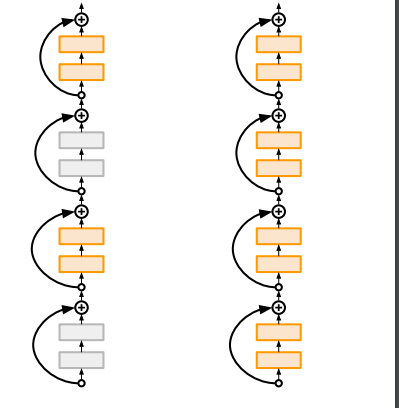
test 진행시에는 모든 layer를 사용한다.

Transfer learning

한국어로 전이학습이라고 한다.

전이학습은 기존에 있는 학습된 모델에 데이터를 조금 추가하여 추가학습 시키는 것이다. 이를 Fine Tunning 이라 한다.

1. 기존 데이터를 학습 시킨 모델이 있다.

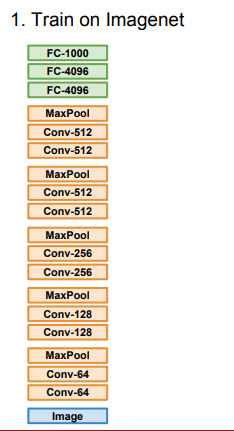
2. 데이터 셋이 조금인 경우에는 가장 마지막 FC layer 하나만 초기화하여 우리의 데이터셋으로 바꾼다.
   

3. 만약 데이터 셋이 많은 경우는 데이터 셋 여러개를 초기화해서 우리의 데이터셋으로 바꾼다.

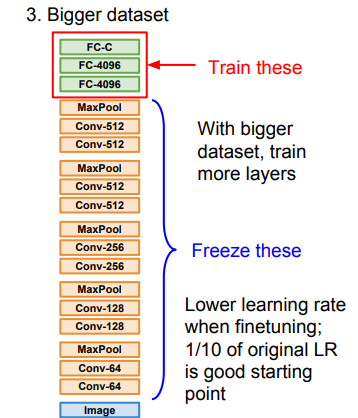
전이 학습을 할 때 4가지의 경우가 발생한다.

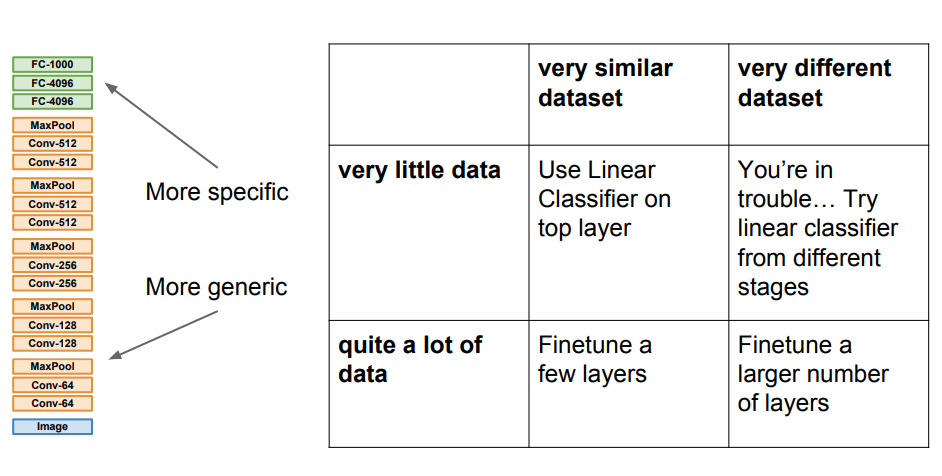
1. 데이터가 적고, 데이터 셋은 기존 데이터와 비슷하다.
   • 선형 분류기를 top layer에 적용한다.
2. 데이터가 많고, 데이터 셋은 기존 데이터와 비슷하다.
   • 몇개의 layers만 Finetune 한다.
3. 데이터가 적고, 데이터 셋은 기존 데이터와 많이 다르다.
   • 제일 문제가 되는 부분이다. 다른 방법을 찾으라고 교수님은 말한다.
4. 데이터가 많고, 데이터 셋은 기존 데이터와 많이 다르다.
   • 많은 수의 layers를 Finetune 시킨다.

Transfer learning은 보통 다음과 같을 때 사용한다.

• 데이터가 적을 때 : 충분한 양의 데이터를 얻는 것 조차 시간과 비용이 많이 소모 된다. 따라서 적은 데이터셋으로 효과적으로 학습시킬 때 전이학습이 유용한다.
• 계산의 제약이 있을 때 : 미리 훈련된 모델의 일부 또는 전체를 가져오기 때문에 계산 리소스가 적게 사용 된다.
• 유사한 도메인일 때 : 만약 뉴스 기사에서 자연어처리 모델이 학습되었다면, 다른 일반적인 문서 분류 작업에서도 해당 모델을 사용할 수 있다.

결론적으로 Transfer learning은 데이터가 적을 때, 시간을 절약하고 싶을 때 아주 유용한 방법이다.

---

7강 끝!