Node 06. 딥러닝 모델 학습

6-1. 들어가며

---

학습 목표

• 딥러닝 모델 학습을 위한 개념 파악
• 손실 함수, 옵티마이저, 지표에 대한 내용 파악

학습 내용

• 손실 함수

  • 평균절대오차
  • 평균제곱오차
  • 원-핫 인코딩
  • 교차 엔트로피 오차
  • 이진 분류 문제의 교차 크로스 엔트로피

• 옵티마이저와 지표

  • 경사하강법
  • 볼록함수와 비볼록함수
  • 안장점
  • 학습률
  • 지표

• 딥러닝 모델 학습

  • 데이터 생성
  • 모델 생성
  • 모델 학습
  • 모델 평가
  • 모델 예측

6-2. 손실 함수(Loss Function)

---

손실 함수란?

• 학습이 진행되며 해당 과정이 얼마나 잘되고 있는지 나타내는 지표를 의미
• 모델 훈련 중 최소화될 값으로 주어진 문제에 대한 성공 지표
• 손실 함수에 따른 결과 ➡️ 파라미터 조정을 하면서 학습 진행됨
• 최적화 이론: 최소화하고자 하는 함수로 미분 가능한 함수 사용!

Keras 제공 손실 함수

• sparse_categorical_crossentropy
  • 클래스 배타적 방식 구분
  • (0,1,2, ....,9)와 같은 방식으로 구분되어 있는 경우 사용
• categorical_cross_entropy
  • 클래스가 원-핫 인코딩 방식일 때 사용
• binary_crossentropy
  • 이진 분류 수행 시 사용

평균 절대 오차(Mean Absolute Error, MAE)

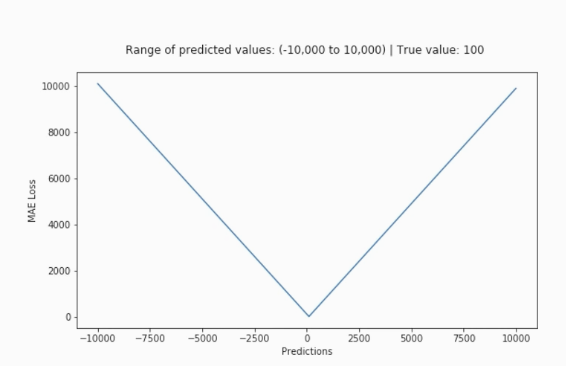
• 오차가 커져도 손실함수는 일정한 증가 추세를 보이는 경우
• 이상치에 강한 특성을 보임
• 데이터에서 [입력-정답]의 관계가 부적절한 경우 발생
  • 이상치에 해당하는 지점 ~ 손실 함수 최솟값으로 가는 정도 영향력이 작음
• 회귀에 많이 사용하는 손실 함수

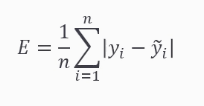
평균 제곱 오차(Mean Squared Error, MSE)

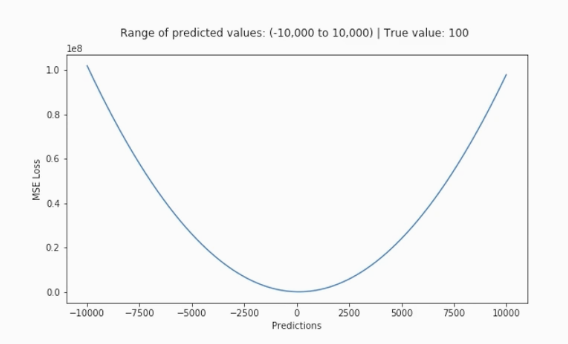
• 가장 많이 사용됨
• 오차가 커질수록 ➡️ 손실함수가 빠르게 증가
• 정답값과 예측값 차이가 클수록 ➡️ 더 많은 패널티 부여
• 회귀에서 사용되는 손실함수
  

평균 절대 오차 vs 평균 제곱 오차

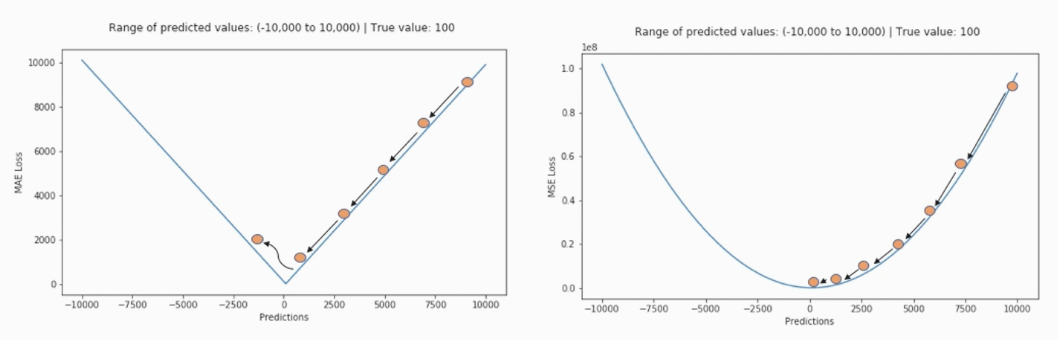
• MAE : loss가 일정하게 감소
• MSE : loss 즉, 차이가 클수록 더 큰 가중치를 주는 것

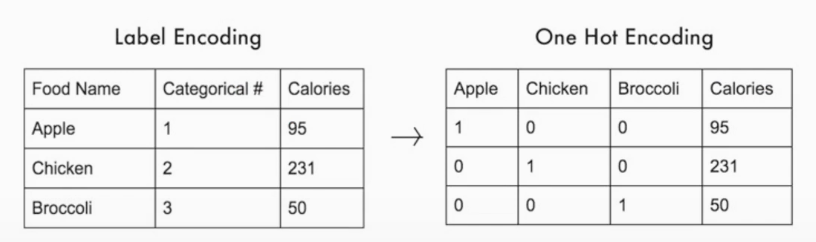
원-핫 인코딩(One-Hot Encoding)

• 범주형 변수 표현 시 사용
• = 가변수
• 정답 label만 1, 나머지는 0
  

교차 엔트로피 오차(Cross Entropy Error, CEE)

• 이진 분류, 다중 클래스 분류에 사용

• softmax 결과 및 원-핫 인코딩 사이 출력 간 거리를 비교한 것을 오차로 잡음

• 정답을 맞추는 경우 ➡️ 오차 0

• 틀리는 경우 ➡️ 차이가 클수록 오차가 무한하게 커짐
  

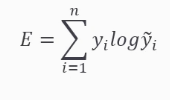
• 이진 분류 문제 교차 엔트로피 계산
  

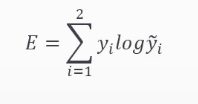
옵티마이저(Optimizer)와 지표

---

옵티마이저(Optimizer)

• 손실 함수 기반 모델이 어떤 방식으로 업데이트되는지를 결정
• Keras에서 여러 옵티마이저 제공
  • keras.optimizer.SGD() : 기본 확률적 경사 하강법
  • keras.optimizer.Adam() : 사용 빈도가 높은 옵티마이저
  • 옵티마이저 튜닝을 위해서 따로 객체 생성하고, 컴파일시에 포함하는 방식으로 구현

경사하강법(Gradient Decent)

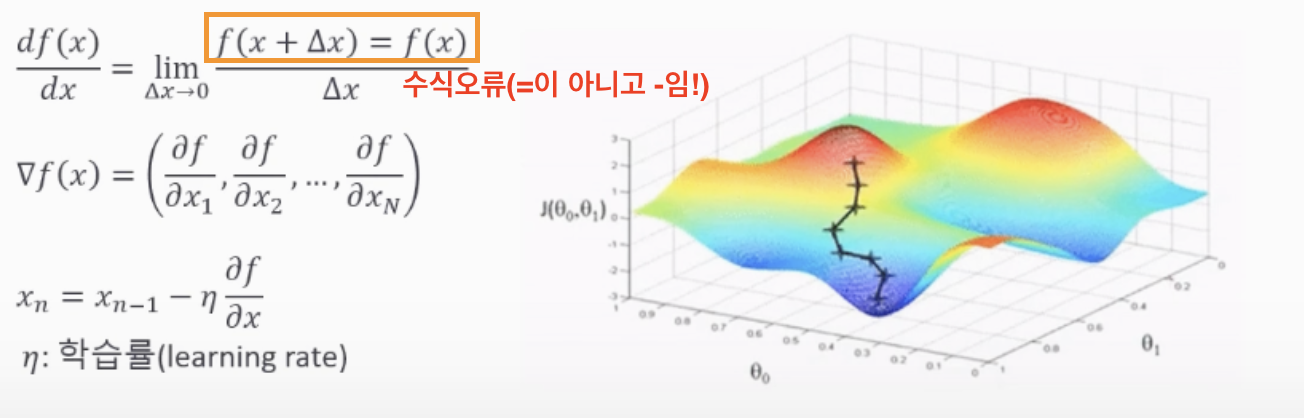
• 최적해를 찾는 방법 중 하나
• 미분 및 기울기로 동작
• 스칼라를 벡터로 미분
• 변화 있는 지점 : 미분 값 존재
• 변화 없는 지점 : 미분 값 0
• 미분 값 클수록 ➡️ 변화량도 큼
• 한 스텝마다의 미분값에 따라서 이동 방향 결정, $f(x)$ 값이 변하지 않을 때까지 반복

볼록 함수와 비볼록 함수(Convex Function & Non-Convex Function)

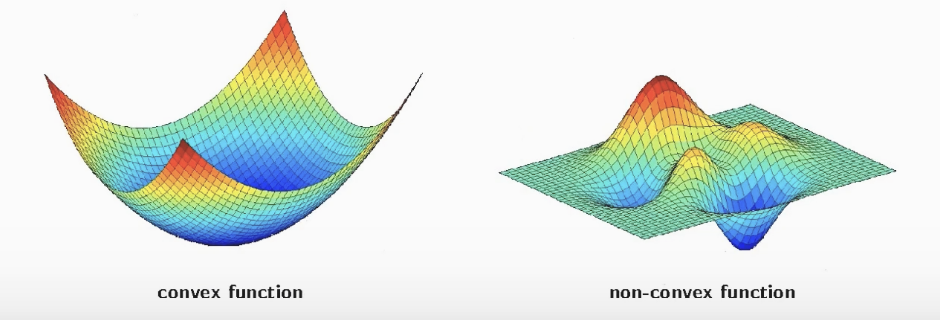
• 볼록 함수 : 어떤 지점에서 시작해도 *최적값에 도달할 수 있음
  • *최적값 : 손실함수가 최소로 하는 점을 말함
• 비볼록 함수 : 시작점 위치에 따라서, 다른 최적값에 도달할 수 있는 것
  • 운이 좋지 못하면 최적해가 아닌 해를 찾기도..

안장점(Saddle Point)

• 기울기가 0이나, 극값은 아닌 안장점이 있음
• 경사하강법은 안장점에서 벗어나지 못함

Q. 경사하강법으로 안장점(Saddle point)에서 벗어나지 못하는지?

A. 기울기의 반대 방향으로 이동해야 하나, 기울기가 0이기 때문에 더이상 업데이트가 일어날 수 없기 때문에 벗어나지 못하고 최적화가 정체될 수 있음.

학습률(Learning Rate)

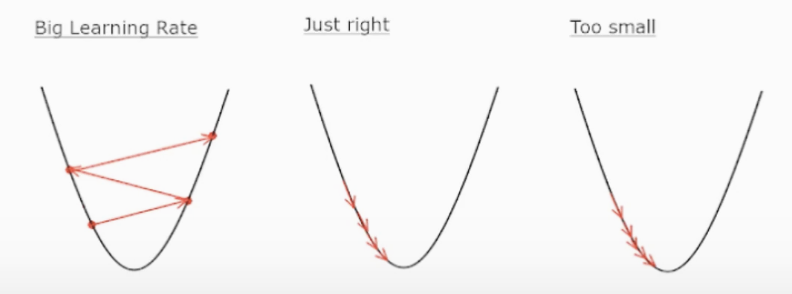
• 모델 학습을 위해 적절한 학습률 부여해야만 최저점에 도달 가능
• 학습률이 과도하게 큰 경우 : 발산
• 학습률이 과도하게 작은 경우 : 학습 시간 오래 걸림, 최저점 미도달 문제 발생

지표(Metrics)

• 딥러닝 학습 시 필요한 다양한 지표들 지정 가능
• mse 또는 accuracy 사용
  • acc로 사용 가능
• keras 지표 종류 : https://keras.io/ko/metrics/

6-4. 딥러닝 모델 학습

---

딥러닝 모델 학습에 필요한 구성 및 관련 요소

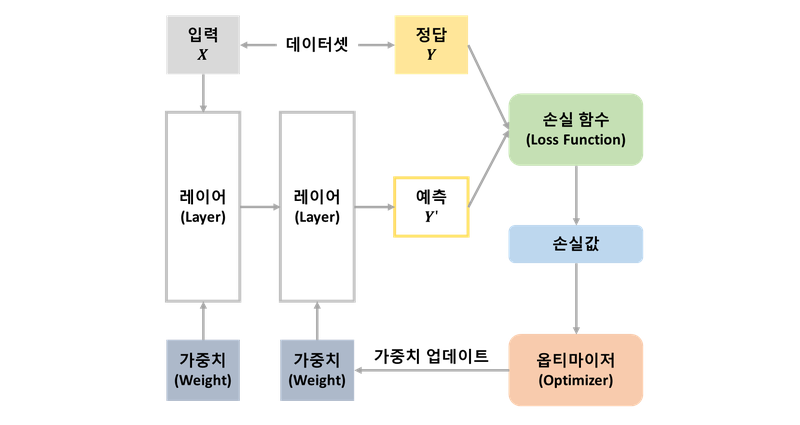
1. 데이터셋을 입력 X와 정답 label인 y로 구분함
2. 입력 데이터 : 연속 레이어로 구성된 네트워크를 통해 결과로 예측한 y' 출력
3. 손실 함수 : 모델이 예측한 y'과 실제 정답인 y를 비교 ➡️ 차이의 정도에 따라 측정되는 손실값이 다름
4. 옵티마이저 : 손실값을 이용해 모델 가중치를 업데이트
5. 모델이 새로 예측한 y'과 실제 정답 y 차이를 측정하는 손실값 계산 ➡️ 반복
6. 계산된 손실값을 최소화할 수 있도록 옵티마이저가 동작

데이터 생성

• 선형회귀를 위한 딥러닝 모델 생성
• make_regression
  • 입력 X, 정답 y
  • n_samples(샘플 개수) : 200개
  • n_featrues(특징 개수) : 1개
  • bias : 5.0
  • noise : 5.0
  • random_state : 123(랜덤 시드 지정)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression

X, y = make_regression(n_samples=200, n_features=1, 
                       bias=5.0, noise=5.0, random_state=123)
y = np.expand_dims(y, axis=1)

plt.scatter(X, y)
plt.show()

• 데이터 구분
  • x_train, y_train : 학습용 데이터셋
  • x_test, y_test : 테스트용 데이터셋

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=0.2, 
                                                    shuffle=True,
                                                    random_state=123)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

모델 생성

• 필요한 라이브러리 import

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import models, layers, optimizers, utils

• Sequential()로 모델 생성
• Dense 레이어 1개 추가
  • 레이어 유닛수 1개, activation은 linear
  • input_shape : (1,) ➡️ 1차원 모양
• summary() : 최종 모델 구조 확인

model = keras.Sequential()
model.add(layers.Dense(1, activation='linear', input_shape=(1,)))
model.summary()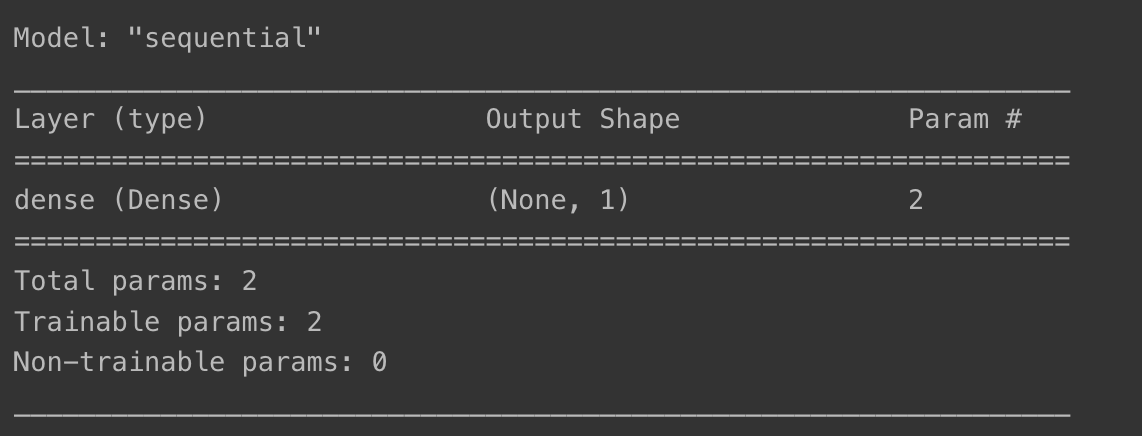

• 모델 시각화

utils.plot_model(model)

모델 학습

• SGD(Stochastic Gradient Descent)
  • 딥러닝 모델 학습 진행 방식 결정 시 사용하는 옵티마이저 중 하나
• compile : 손실함수, 옵티마이저, 지표 지정
• 손실함수는 mse로 지정
• 옵티마이저는 정의했던 SGD 사용
• 지표는 mae와 mse 사용
• fit() : 모델 학습 진행
  • x_train과 y_train 지정
  • 학습 반복 횟수(epochs) : 40

optimizer = optimizers.SGD()
model.compile(loss='mse', optimizer=optimizer, metrics=['mae', 'mse'])
history = model.fit(x_train, y_train, epochs=40)

Epoch 1/40
5/5 [==============================] - 2s 2ms/step - loss: 573.3981 - mae: 19.1674 - mse: 573.3981
Epoch 2/40
5/5 [==============================] - 0s 1ms/step - loss: 461.0914 - mae: 17.2276 - mse: 461.0914
Epoch 3/40
5/5 [==============================] - 0s 1ms/step - loss: 371.4703 - mae: 15.5221 - mse: 371.4703
Epoch 4/40
5/5 [==============================] - 0s 2ms/step - loss: 300.3263 - mae: 13.9134 - mse: 300.3263
Epoch 5/40
5/5 [==============================] - 0s 1ms/step - loss: 243.1690 - mae: 12.5352 - mse: 243.1690
Epoch 6/40
5/5 [==============================] - 0s 1ms/step - loss: 198.1948 - mae: 11.3014 - mse: 198.1948
Epoch 7/40
5/5 [==============================] - 0s 2ms/step - loss: 162.0112 - mae: 10.2153 - mse: 162.0112
Epoch 8/40
5/5 [==============================] - 0s 1ms/step - loss: 133.2978 - mae: 9.2251 - mse: 133.2978
Epoch 9/40
5/5 [==============================] - 0s 1ms/step - loss: 110.1979 - mae: 8.4215 - mse: 110.1979
Epoch 10/40
5/5 [==============================] - 0s 2ms/step - loss: 92.0803 - mae: 7.6909 - mse: 92.0803
Epoch 11/40
5/5 [==============================] - 0s 1ms/step - loss: 77.5406 - mae: 7.0378 - mse: 77.5406
Epoch 12/40
5/5 [==============================] - 0s 1ms/step - loss: 65.9422 - mae: 6.5127 - mse: 65.9422
Epoch 13/40
5/5 [==============================] - 0s 1ms/step - loss: 56.8376 - mae: 6.0565 - mse: 56.8376
Epoch 14/40
5/5 [==============================] - 0s 2ms/step - loss: 49.4224 - mae: 5.6138 - mse: 49.4224
Epoch 15/40
5/5 [==============================] - 0s 1ms/step - loss: 43.4766 - mae: 5.2351 - mse: 43.4766
Epoch 16/40
5/5 [==============================] - 0s 2ms/step - loss: 38.8747 - mae: 4.9559 - mse: 38.8747
Epoch 17/40
5/5 [==============================] - 0s 2ms/step - loss: 35.1471 - mae: 4.6994 - mse: 35.1471
Epoch 18/40
5/5 [==============================] - 0s 2ms/step - loss: 32.1710 - mae: 4.4728 - mse: 32.1710
Epoch 19/40
5/5 [==============================] - 0s 1ms/step - loss: 29.8394 - mae: 4.3011 - mse: 29.8394
Epoch 20/40
5/5 [==============================] - 0s 2ms/step - loss: 27.9350 - mae: 4.1438 - mse: 27.9350
Epoch 21/40
5/5 [==============================] - 0s 1ms/step - loss: 26.4692 - mae: 4.0377 - mse: 26.4692
Epoch 22/40
5/5 [==============================] - 0s 2ms/step - loss: 25.2609 - mae: 3.9402 - mse: 25.2609
Epoch 23/40
5/5 [==============================] - 0s 1ms/step - loss: 24.3205 - mae: 3.8724 - mse: 24.3205
Epoch 24/40
5/5 [==============================] - 0s 1ms/step - loss: 23.5766 - mae: 3.8274 - mse: 23.5766
Epoch 25/40
5/5 [==============================] - 0s 2ms/step - loss: 22.9866 - mae: 3.7823 - mse: 22.9866
Epoch 26/40
5/5 [==============================] - 0s 2ms/step - loss: 22.4922 - mae: 3.7448 - mse: 22.4922
Epoch 27/40
5/5 [==============================] - 0s 1ms/step - loss: 22.1143 - mae: 3.7163 - mse: 22.1143
Epoch 28/40
5/5 [==============================] - 0s 2ms/step - loss: 21.8074 - mae: 3.6945 - mse: 21.8074
Epoch 29/40
5/5 [==============================] - 0s 2ms/step - loss: 21.5809 - mae: 3.6766 - mse: 21.5809
Epoch 30/40
5/5 [==============================] - 0s 1ms/step - loss: 21.3961 - mae: 3.6617 - mse: 21.3961
Epoch 31/40
5/5 [==============================] - 0s 1ms/step - loss: 21.2558 - mae: 3.6549 - mse: 21.2558
Epoch 32/40
5/5 [==============================] - 0s 1ms/step - loss: 21.1199 - mae: 3.6411 - mse: 21.1199
Epoch 33/40
5/5 [==============================] - 0s 1ms/step - loss: 21.0021 - mae: 3.6331 - mse: 21.0021
Epoch 34/40
5/5 [==============================] - 0s 5ms/step - loss: 20.9313 - mae: 3.6252 - mse: 20.9313
Epoch 35/40
5/5 [==============================] - 0s 2ms/step - loss: 20.8649 - mae: 3.6205 - mse: 20.8649
Epoch 36/40
5/5 [==============================] - 0s 2ms/step - loss: 20.8200 - mae: 3.6136 - mse: 20.8200
Epoch 37/40
5/5 [==============================] - 0s 2ms/step - loss: 20.7878 - mae: 3.6108 - mse: 20.7878
Epoch 38/40
5/5 [==============================] - 0s 1ms/step - loss: 20.7570 - mae: 3.6090 - mse: 20.7570
Epoch 39/40
5/5 [==============================] - ETA: 0s - loss: 22.3289 - mae: 3.9033 - mse: 22.328 - 0s 2ms/step - loss: 20.7228 - mae: 3.6043 - mse: 20.7228
Epoch 40/40
5/5 [==============================] - 0s 2ms/step - loss: 20.7291 - mae: 3.6044 - mse: 20.7291

• 지표 시각화

plt.plot(history.history['mae'])
plt.plot(history.history['mse'])
plt.xlabel('Epoch')
plt.legend(['mae', 'mse'])
plt.show();

모델 평가

• evaluate() 함수 사용
• x_test, y_test에 대한 지표인 mae, mse 확인

model.evaluate(x_test, y_test)

2/2 [==============================] - 0s 3ms/step - loss: 21.9171 - mae: 3.9882 - mse: 21.9171

모델 예측

• predict() : 학습된 모델을 이용한 입력 데이터 X 예측값 받아오는 함수
• 실제 데이터 결과값 y 및 모델 예측 결과 result 시각화

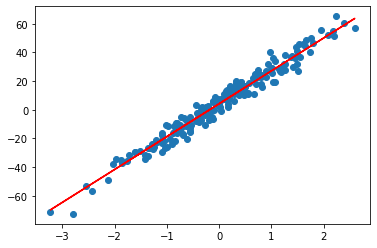
result = model.predict(X)

plt.scatter(X, y)
plt.plot(X, result, 'r')
plt.show()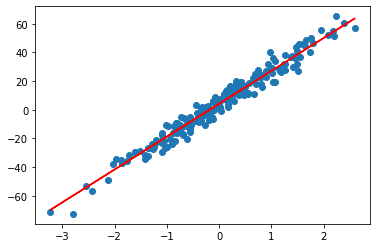

• 딥러닝에서 사용한 레이어 확인

model.layers

• 레이어 이름 확인
  • 모델의 0번째 레이어인 layers[0]을 가져오면 ➡️ layer.name으로 레이어 이름 확인 가능
• get_layer()함수로 같은 이름 레이어를 볼 수도 있음!

layer = model.layers[0]
print(layer.name)
layer = model.get_layer('dense')
print(layer.name)

• 레이어에서 사용한 가중치 및 바이어스 확인
  • 이를 통해 선형 회귀식 획득

weights, biases = layer.get_weights()
print(weights)
print(biases)

• 선형회귀식
  • np.array(weights * X + biases)

plt.scatter(X, y)
plt.plot(X, np.array(weights * X + biases), 'r')
plt.show()