Node 04. 지도학습(회귀)

4-1. 들어가며

---

학습 목표

• 지도학습(회귀) 모델 활용
• 최적 하이퍼파라미터
• 모델 평가

학습 내용

• 선형 회귀
• 릿지 회귀
• 라쏘 회귀
• 엘라스틱넷 회귀
• 랜덤포레스트 & xgboost
• 하이퍼파라미터 튜닝
• 평가(회귀)

4-2. 선형 회귀

---

선형 회귀

• 단순 선형 회귀 : 독립변수 1개
• ⭐️다중 선형 회귀 : 독립변수 2개 이상
  • 자주 사용!

손실 함수

• 비용함수, 목적함수와 동일한 의미
• 데이터 모델 간 거리 계산
• error(오차) 계산(실제값과 예측값 사이의 차이)
• 평균 제곱 오차를 최소화할 파라미터 서치

경사하강법

• 오차 찾기
• 손실함수의 기울기 |절대값|이 가장 작은 지점을 찾아 오차가 작은 모델을 만드는 방법론!

실습

from sklearn.metrics import mean_squared_error

• MSE(Mean_Squared_Error) 사용!

  • 오차를 제곱한 것
    

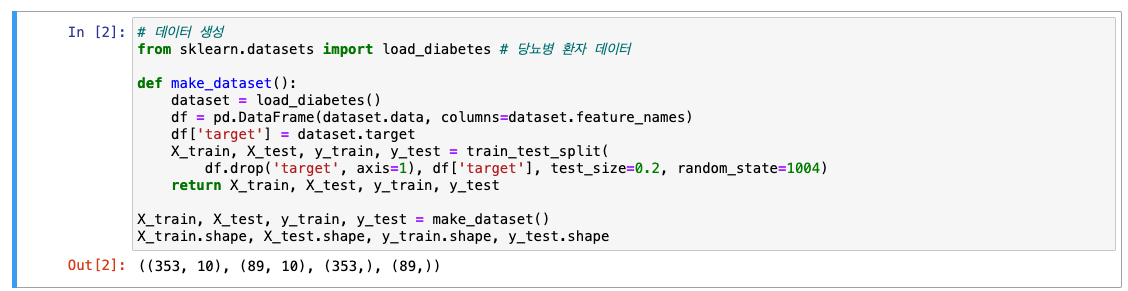
• 데이터셋 불러오기
  

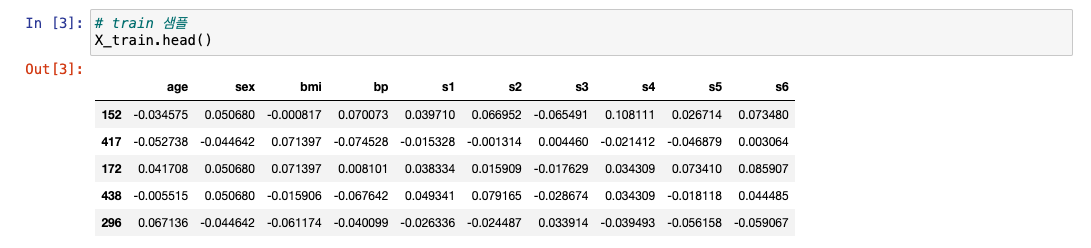
• train 데이터 샘플 확인
  

• Target 데이터 샘플 확인 & Target 비율 확인

  • 50~100 사이가 가장 많고, 그 이후 값들은 점점 하강하는 형태
    

• 선형 회귀

  • LinearRegression
    
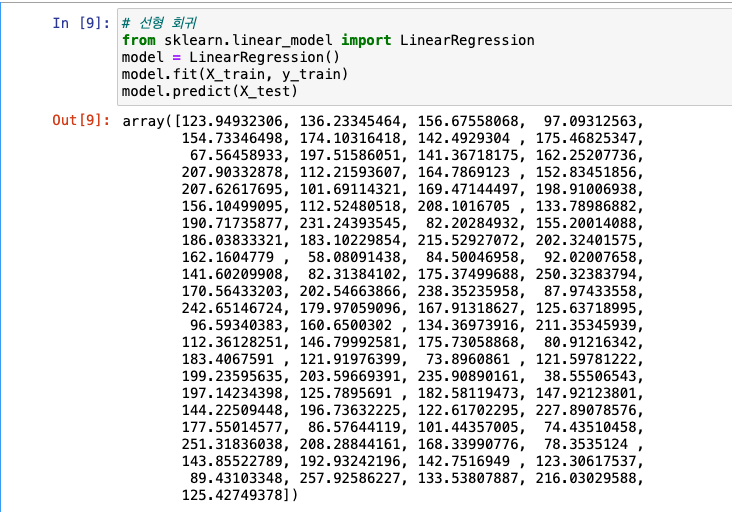
  • MSE로 평가 -> 수치가 작을 수록 좋음
    

4-3. 릿지 회귀(Ridge regression)

---

릿지 회귀

• overfitting 문제를 해결하기 위해 규제(regularization) 적용한 모델
• L2 규제
• 파라미터 값으로 조절
• 파라미터 값이 커질수록 -> 회귀 계수 값을 작게 만든다!
  • ex) W1*X1 + W2*X2 + W3*X3 + ... + Wn*Xn
    • W:회귀계수, X:피쳐(변수)

규제로 성능을 올린다!

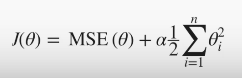
실습

• from sklearn.linear_model import Ridge

  • 선형 회귀에 비해 수치가 커짐 -> 선형 회귀보단 좋지 못한 모델이다!
    

• 회귀 계수 확인 : 피쳐 순서대로 나옴
  

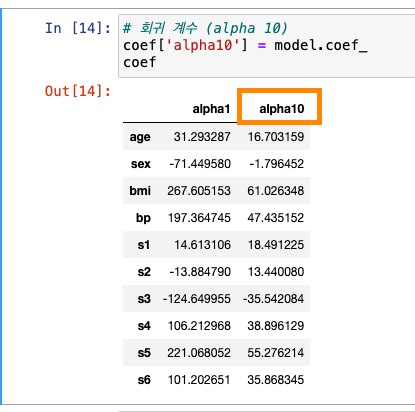
• Ridge() 기본값 : alpha가 1

  • alpha를 10으로 바꾼다면?
    

• alpha 값이 10이라는 것을 회귀 계수에 저장

  • .coef_
    

• 이번에는 alpha를 0.1로 -> 앞선 선형 회귀와 비슷한 수치
  

• alpha = 0.05
  
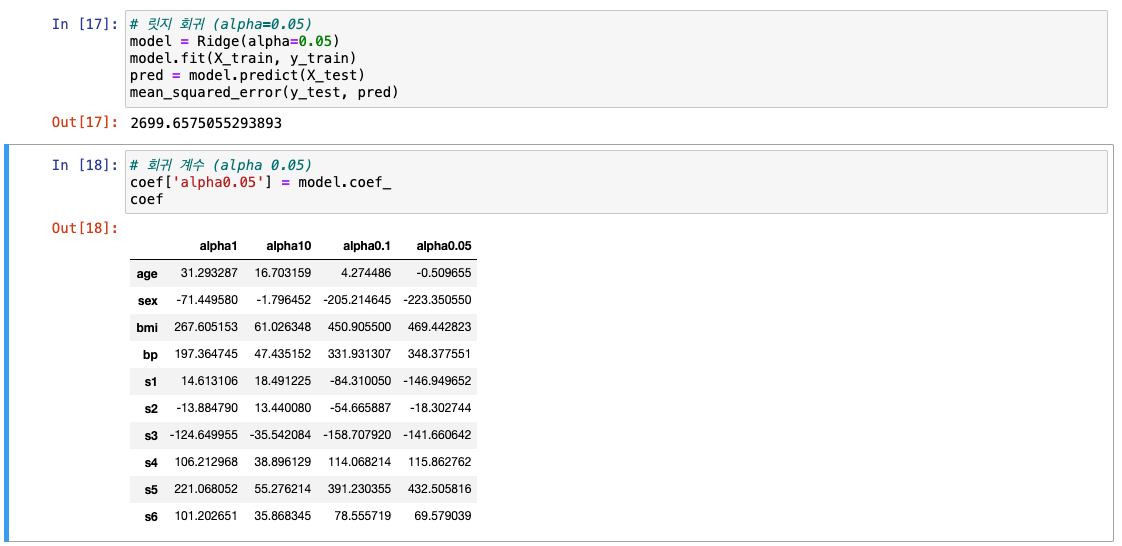
  • 최고 성능이기 때문에 0.05로 저장!

4-4. 라쏘 회귀

---

라쏘 회귀

• overfitting 문제를 해결하기 위해 규제(regularization) 적용한 모델
• L1 규제(중요 피쳐만 선택!)
• L2와는 달리 회귀 계수를 급강하시켜 중요하다 생각하는 피쳐만 선택(나머지는 0으로 만들어버림)
• 릿지 회귀보다 더 극단적이라고 볼 수 있음

실습

• from sklearn.linear_model import Lasso

  • 라쏘도 alpha 기본값 1
    

• alpha=1 회귀계수 저장

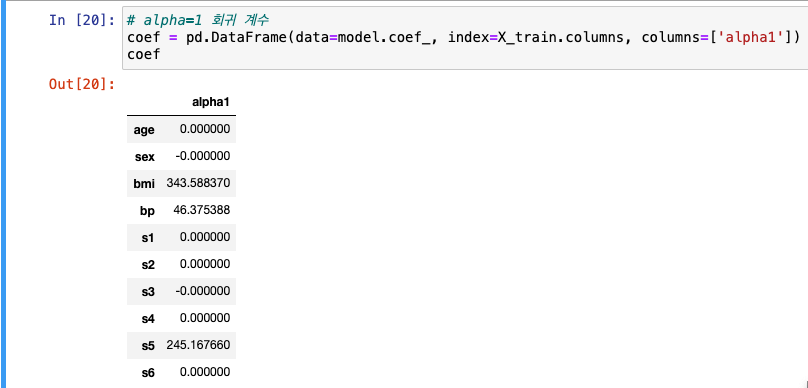
  • 주요 피쳐 제외하고 0으로 만들어진 것을 볼 수 있음
    

• alpha=2

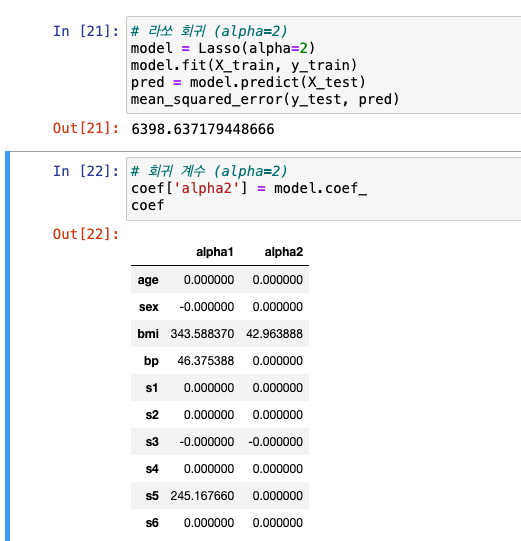
  • 전체적으로 수치가 줄었고, 0으로 만들어진 피쳐도 더 많아짐!
    

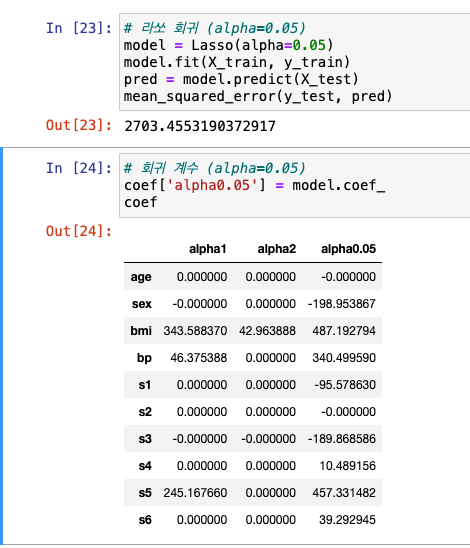
• alpha=0.05
  

4-5. 엘라스틱넷 회귀

---

엘라스틱넷 회귀

• overfitting 문제를 해결하기 위해 규제(regularization) 적용한 모델
• L2 + L1 결합
• 시간 오래걸림!!!

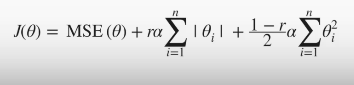
실습

• from sklearn.linear_model import ElasticNet
  • 이것도 기본 alpha는 1
  • 오차가 큰 편
    

• alpha를 아주 작게, L1 규제 비율 설정하기!
  • l1_ratio={수치}로 사용 가능
  • L1과 L2는 기본적으로 0.5(반반)으로 설정되어 있음
    

🔎 규제 방식 비교

• 릿지 회귀 : L2
• 라쏘 회귀 : L1(중요한 피처만 쓰고, 나머지는 0으로)
• 엘라스틱넷 회귀 : L2+L1

4-6. 랜덤포레스트 & xgboost

---

랜덤포레스트 VS XGBoost

• 랜덤포레스트

  • 여러 개의 Decision Tree
  • 앙상블 방법: bagging 방식
  • 부트스트랩 샘플링(데이터셋의 중복을 허용)
  • 최종 다수결 Voting

• XGBoost

  • 트리 앙상블 중에서 성능이 좋은편
  • 약한 학습기가 -> 계속해서 업데이트 -> 좋은 모델을 빌딩

실습: MSE로 평가

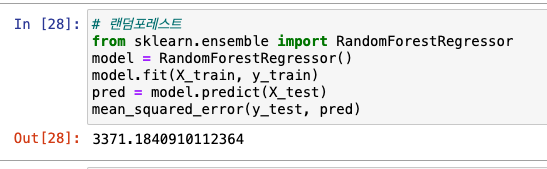
• 랜덤 포레스트
  -from sklearn.ensemble import RandomForestRegressor
  - 회귀에서는 RandomForestRegressor를 불러와서 사용!
  

• XGBoost

  • from xgboost import XGBRegressor
    - 회귀에서는 XGBRegressor를 불러와서 사용!
    

4-7. 하이퍼파라미터 튜닝

---

사이킷런 model_selection

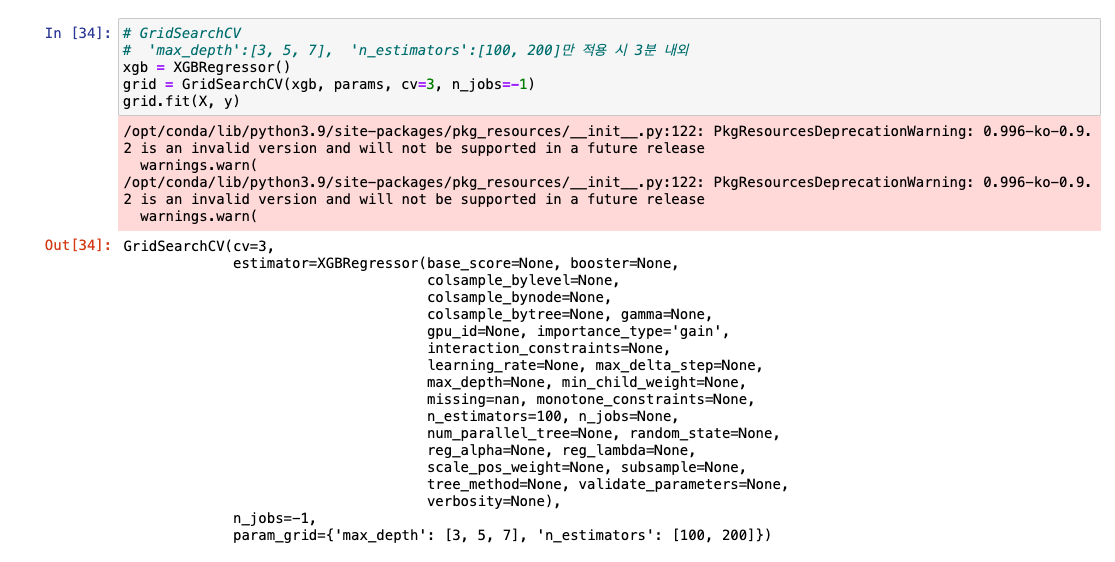
GridSearchCV

• grid search 방식으로 최적 하이퍼파라미터 찾음
• 시간 오래 걸림..

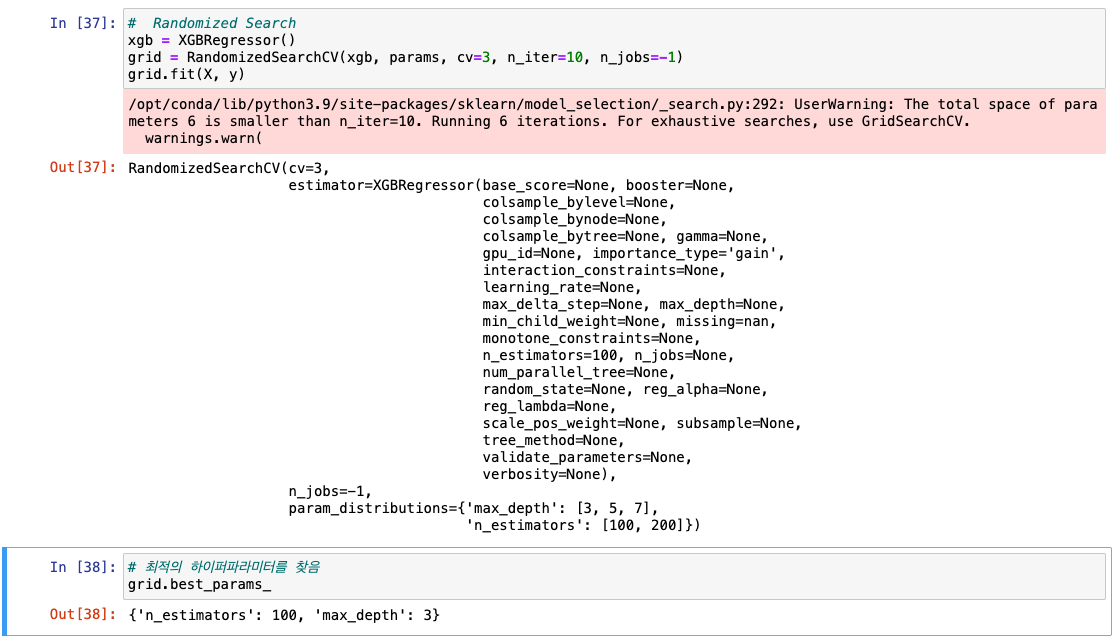
RandomizedSearchCV

• 랜덤 N개의 조합으로 탐색
• 시간 안에 찾게 되는 값이 최적 하이퍼파라미터

실습

• 기본 설정 : 라이브러리를 불러오고, 하이퍼파라미터를 지정, 그 후 데이터셋 로드
  

• GridSearchCV

  • n_jobs=-1 : 병렬 코어(코어 전부 사용하겠다는 의미)
    

  • 최적 파라미터 탐색
    

  • 하이퍼파라미터 튜닝 진행: MSE로 평가해보기
    

• RandomizedSearchCV
  

4-8. 평가(회귀)

---

정리

평가 지표	설명	수식
MAE	평균 절대 오차 (Mean Absolute Error) - 실제 값과 예측 값 사이 -> 절대값으로 평균
MSE	평균 제곱 오차 (Mean Squared Error) - 실제 값과 예측 값 사이 -> 제곱한 다음 평균
RMSE	루트 평균 제곱 오차 (Root Mean Squared Error) - MSE에 루트를 씌운 형태 - MSE가 실제 오류보다 커짐 -> 그래서 루트를 사용
RMSLE	루트 평균 제곱 로그 오차 (Root Mean Squared Log Error) - RMSE에 로그를 씌운 형태 - 예측 값이 실제 값보다 작을 때 -> 더 큰 패널티
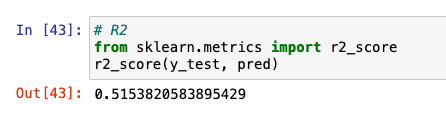
R2	결정계수 (R Squared Score) - 실제 값 분산 대비 예측 값의 분산을 계산(1에 유사할수록 성능 good) - 위는 오차, 아래는 편차

실습

• MAE

  • from sklearn.metrics import mean_absolute_error
    

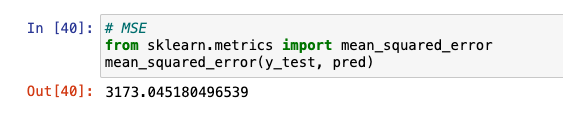
• MSE
  from sklearn.metrics import mean_squared_error
  

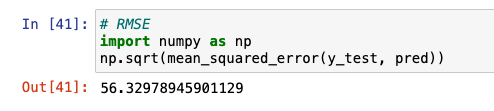
RMSE와 RMSLE는 바로 사용할 수는 없지만, 사이킷런과 넘파이로 조합해 사용 가능

• RMSE
  

• RMSLE

  • from sklearn.metrics import mean_squared_log_error를 사용한 뒤 한번 더 루트 씌워줘야 함!
    

• R2

  • from sklearn.metrics import r2_score