선형회귀

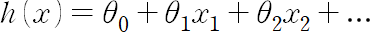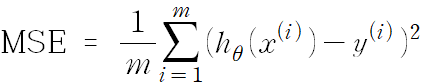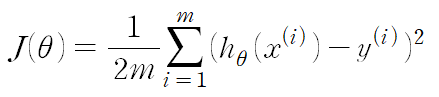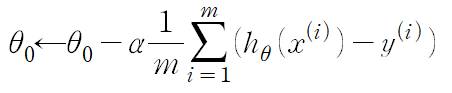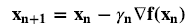
선형 회귀(Linear Regression)

• 지도 학습 중 회귀에 해당한다.
• data에 가장 알맞는 선(최적선)을 찾는 것
• 단순하고 유용하며 다른 알고리즘의 기반이 된다.
• 목표 변수(target variable) : 맞추려고 하는 값
• 입력 변수(feature) : 맞추는데 사용되는 값

가설 함수(hypothesis function)

• 데이터에 대한 최적선을 찾으려고 시도해보는 모든 함수
• x를 바꾸는 것이 아니라 theta값을 바꾸며 최적화한다.

평균 제곱 오차(MSE)

• 가설 함수 평가법 → 데이터들과 가설함수가 평균적으로 얼마나 떨어져있는지 확인하는 방법
• 가설 함수의 예측 값과 실제 값 차의 제곱의 합

  왜 오차의 제곱을 더하는 것인가?
  → 값의 차이를 양수/음수에 상관없이 똑같이 취급을 해야하고, 오차가 커질수록 더 부각시키기 위해서이다.

• MSE 값이 크면 가설 함수가 데이터에 잘 맞지 않다.
• MSE 값이 작으면 가설 함수가 데이터에 잘 맞다.

손실 함수(Loss Function)

• 가설 함수의 성능을 평가하는 함수
• 손실 함수가 크면 가설함수가 데이터에 잘 맞지 않다.
• 손실 함수가 작으면 가설함수가 데이터에 잘 맞다.
• theta의 값은 여러개지만 편의를 위해 식에서는 1개로 나타냄
  - 주의! : 손실함수 J의 input은 theta이다.

경사 하강법(Gradient Descent)

• 손실함수의 output을 최소화하는 방법 중 하나
  

• 손실함수 그래프에서 기울기의 반대 방향으로 가다보면 극소점에 도달하게 된다 → 가설함수가 데이터에 가장 잘 맞게 된다.
  

• 위와 같은 과정을 반복하며 극소점으로 향하게 된다.

• 수학적인 식으로 간단히 표현을 하면 위와 같은 식이 된다.

• 학습률 알파의 크기에 따른 경사하강법
  • 학습률 알파를 learning rate라고도 한다.
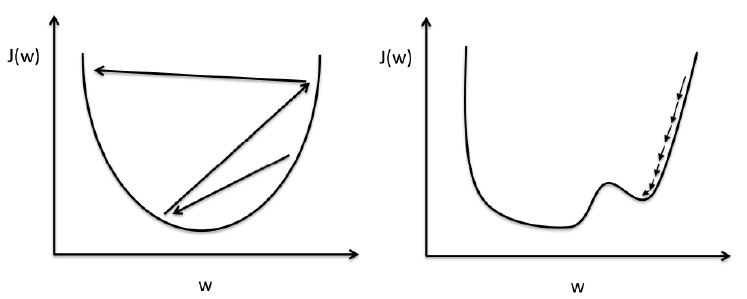
  • 학습률이 클 때 : overshooting의 발생
  • 학습률이 작을 때 : many iterations 또는 local minimum에 빠지게 된다.

★어떻게 적절한 학습률을 찾을 수 있는가?
: 일반적으로 0.0~1 사이의 숫자로 정하고, 여러개를 실험해보면서 경사 하강을 제일 적게 하면서 손실이 잘 줄어드는 학습률을 선택한다.

평균 제곱근 오차(RMSE)

• 평균 제곱 오차의 제곱근
• training set과 test set을 분할 한 뒤 training set으로 학습을 한 뒤, test set으로 RMSE를 판단한다.

본 포스트는 코드잇 강의를 공부하며 정리한 내용입니다! 자세한 설명은 "코드잇 머신러닝 강의를 참고해주세요!

+) 코드잇 강의 바로가기