런던의 데이터엔 자전거가 있다

수수·2023년 8월 4일
ACFARIMAKPSSPACFProphetSARIMASARIMAXadfpdqseasonalitystationary계절성공유자전거런던모델시계열시계열분석예측자전거정상성차분추세학습
0
post-thumbnail

데이터 출처 : London bike sharing

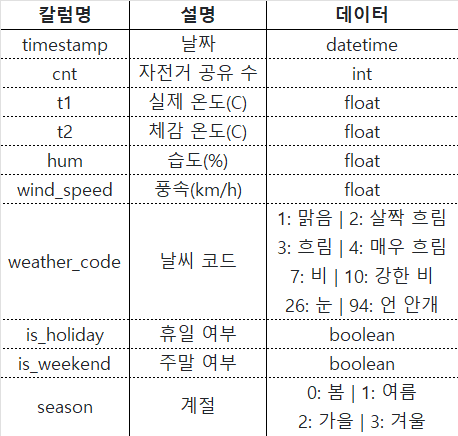
런던의 공유 자전거 공유 수를 예측하는 모델을 만들어보자. 시간 정보를 담고 있는 데이터이므로 시계열 모델을 만들도록 한다.

1. 데이터 EDA & 전처리

우선 원활한 분석을 위해 현재 시간 단위의 정보를 일 단위로 요약한다. 연속형 변수는 평균값으로, 범주형 변수는 최빈값으로 요약한다. 

df = pd.read_csv(
	"./data/london_bike.csv", 
	index_col="timestamp", 
    parse_dates=True
    )

df1 = df.iloc[:, :5].resample('D').mean()

def most_common(x):
    if x.empty:  # 그룹이 비어있는 경우 처리
        return None
    return x.value_counts().idxmax()
    
df2 = df.iloc[:, 5:].resample('D').apply(most_common)

df1 = df1.interpolate(method='time') # 보간
df2 = df2.interpolate(method='time')

df = pd.concat([df1, df2], axis=1)

요약을 하고 보면, 정보가 없는 날이 딱 하루가 있는데, 판다스에서 제공하는 interpolate 메서드 함수를 이용해 보간해주자. 이후 자체 검증을 위해 데이터를 train, test 셋으로 나눠줘야 하는데 그 기준은 '적당히' 잡아주면 된다. 7:3, 8:2 비율이 제일 무난하고, 그게 아니더라도 '보기에 그럴 듯 하다면' 크게 상관 없다. 본 분석에선 특정 날짜를 기준으로 train, test셋을 나눴다.

threshold = pd.Timestamp("2016-09-30")
train_df = df[:threshold].copy()
test_df = df[threshold:].copy()
  • 범주형 변수 처리

이제 범주형 변수들을 처리해줘야 한다. 불리언 변수인 is_holiday, is_weekend의 경우는 그대로 둬도 되지만, weather_code, season의 경우, 원핫 인코딩을 해주어야 한다. 현재는 숫자 타입의 변수로 설정되어있으므로 이를 문자 타입으로 바꿔주고, pandas의 라이브러리의 함수 get_dummies를 이용해 원핫 인코딩을 해준다. 이때 첫째 열은 drop해줌으로써 차원의 저주(변수가 많아질수록 데이터가 왜곡되는 현상)를 최소화하자. 이후, train과 test셋의 칼럼을 똑같이 맞춰주어야 하는데, test_df = test_df[train_df.columns] 이 코드를 먼저 실행해보고, 오류창에 없다고 표시되는 칼럼을 미리 test셋에 생성해주면 된다.

train_df['weather_code'] = train_df['weather_code'].astype(str)
train_df['season'] = train_df['season'].astype(str)
test_df['weather_code'] = test_df['weather_code'].astype(str)
test_df['season'] = test_df['season'].astype(str)

train_df = pd.get_dummies(train_df, drop_first=True)
test_df = pd.get_dummies(test_df, drop_first=True)

# test셋엔 'weather_code_26.0', 'season_1.0', 'season_2.0' 범주가 없음.
test_df[['weather_code_26.0', 'season_1.0', 'season_2.0']] = 0
test_df = test_df[train_df.columns]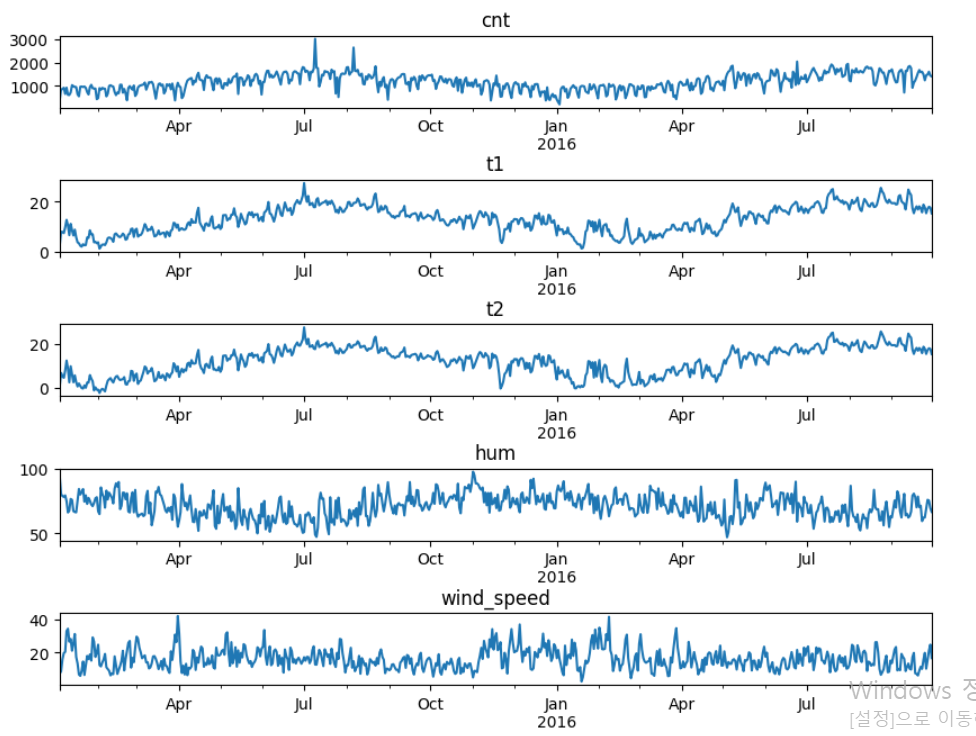

  • 계절성 확인

여기까지 완료하면 연속형 변수의 선 그래프가 위와 같이 그려짐을 확인할 수 있을 것이다. 그런데, 시계열 분석을 위해선, Trend(추세), Seasonality(계절성), Cycle(주기), Irregular Variation(불규칙 변동) 등이 어떤지를 확인해봐야 하는데, 어떻게 확인할 수 있을까? 위의 그림에서 '얼추' 추산은 해볼 수 있겠지만 아무래도 수치적인 데이터가 더 설득력이 있지 않겠는가?

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

def plot_acf_pacf(df, target_column, lags=30):
    target_series = df[target_column].dropna()
    fig = plt.figure(figsize=(10, 4))
    ax1 = fig.add_subplot(1, 2, 1)
    ax2 = fig.add_subplot(1, 2, 2)
    plot_acf(df[target_column].dropna(), ax=ax1, lags=lags);
    plot_pacf(df[target_column].dropna(), ax=ax2, lags=lags);

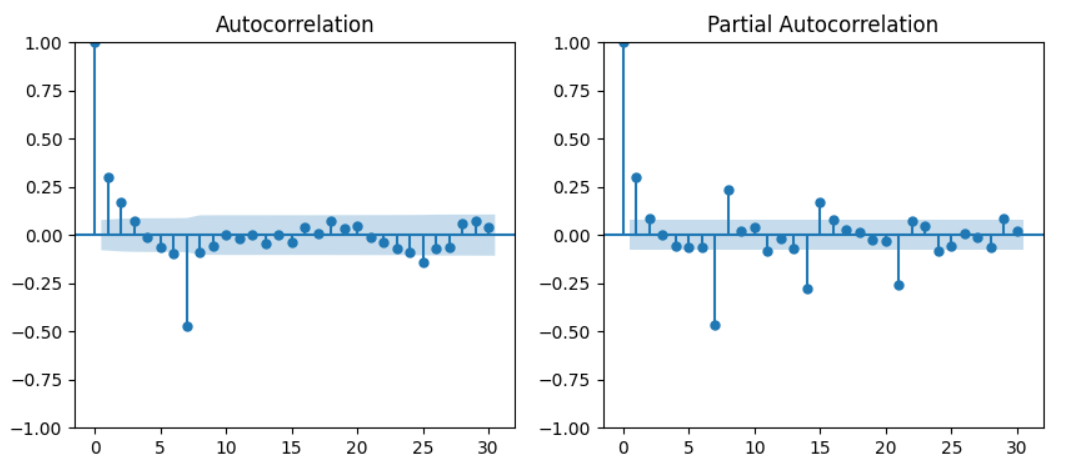
plot_acf_pacf(train_df, 'cnt')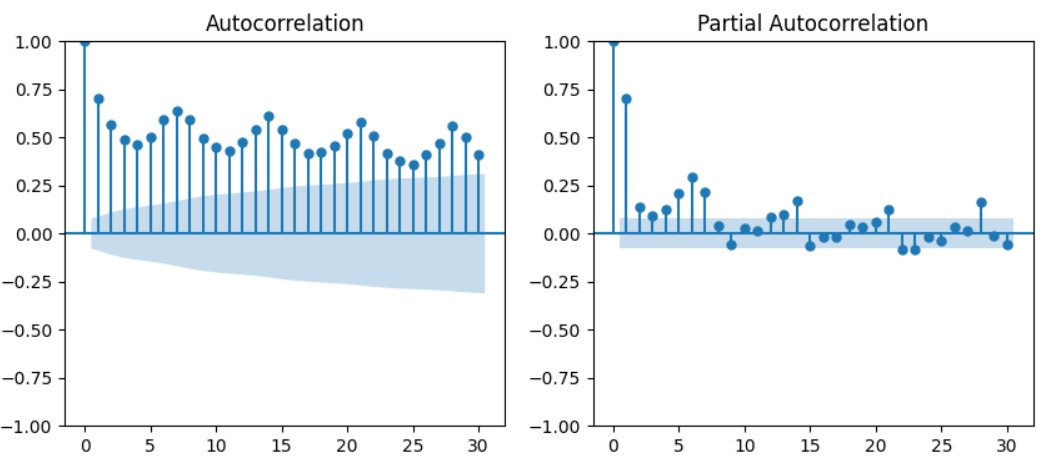

ACF(AutoCorrelation Function) 그래프는 원래 날짜의 데이터와 lag(지연날짜)의 데이터간의 상관을 표시한 그래프이다. 자기 자신의 데이터를 쓰므로 자기상관(AutoCorrelation)이라는 표현을 사용한다. PACF(Partial ACF) 그래프는 ACF보다 더 직접적인 상관을 표시한 그래프이다. ACF는 원래 날짜와 lag 날짜 사이의 데이터도 어느 정도 고려한 값이지만, PACF는 사이 데이터들의 영향력을 철저히 배제한다. 아무튼, 이렇게 확인한 그래프에서 원래 날짜와 상관이 높다고 나오는 날짜들의 간격을 보면 계절성을 확인할 수 있다. 해당 데이터에선 7일(7시점) 간격으로 상관이 주기적으로 높아짐을 확인할 수 있다. 즉, 해당 데이터는 7일을 간격으로 한 계절성을 가지고 있는 데이터이다.

계절성을 가지고 있는 것이 확인되었으므로, 계절성을 고려하여 ARIMA 분석을 할 수 있는 SARIMA(Seasonal ARIMA) 모델을 만들기로 한다.

2. SARIMA

  • 정상성

시계열 분석을 위해선, 정상성을 띄지 않는 데이터를 정상성을 띄는 데이터로 만들어줘야 한다. 정상성을 띄는지 확인하는 데에는 ADF Test, KPSS Test 결과값을 이용한다. ADF의 경우 p-value가 0.05보다 낮아야, KPSS는 p-value가 0.05보다 높아야 정상성을 띈다고 해석할 수 있다고 한다. 두 테스트 중 테스트 하나만 통과해도 정상성을 띄는 데이터라고 판단할 수도 있겠지만, 본 분석에선 좀 더 엄격하게 두 테스트를 모두 통과하는지 확인해보도록 한다.

from statsmodels.tsa.stattools import adfuller, kpss

def stationary_test(df, target_column):
    target_series = df[target_column].dropna()
    adf_result = adfuller(target_series)
    adf_p_value = adf_result[1]
    kpss_result = kpss(target_series)
    kpss_p_value = kpss_result[1]
    print(f"{target_column} ADF p-value: 
    	  {round(adf_p_value, 4)} stationary: {adf_p_value < 0.05}")
    print(f"{target_column} KPSS p-value: 
          {round(kpss_p_value, 4)} stationary: {kpss_p_value > 0.05}")

stationary_test(train_df, 'cnt')

테스트 결과, 아깝게 KPSS 테스트를 통과하지 못했다. 이 정도 해도 '아 그래도 정상성을 띄는 데이터구나' 하고 넘어갈 수 있겠지만, 앞서 우리는 본 데이터가 '계절성'을 띄는 데이터임을 확인했다. 정상성을 띄는 데이터란 이런 계절성, 추세따위가 없는 일정하고 무던한 데이터임을 뜻하므로, 여기선 확실히 정상성을 띄는 데이터로 만들어주기로 한다. 가장 많이 차용되는 방법은, '차분'을 해주는 것이다.

  • 차분
train_df["diff"] = train_df["cnt"].diff()
train_df["seasonal_diff"] = train_df["cnt"].diff(7)

차분이란, 현 시점의 데이터에서 특정 예전 시점의 데이터를 빼주는 것을 의미한다. 보통 차분을 한다고 하면, 1시점 단위의 차분을 진행한다. 그리고 차분 중 '계절 차분'이라는 개념이 있는데, 계절 차분의 경우 계절성의 주기로 판단되는 시점의 값을 빼주면 된다. 본 데이터에선 주기성이 7로 판단되었으므로, 7시점 이전의 데이터를 빼주면 되는 것이다. 이렇게 차분을 한 후, 정상성을 판단하면, 두 데이터 모두 정상성을 띈다고 결과값이 나온다. 이제 이 두 차분값을 이용해 각각 ACF, PACF 그래프를 한 번 더 그려주면, SARIMA 모델을 만드는 데에 필요한 파라미터값을 얻을 수 있다.

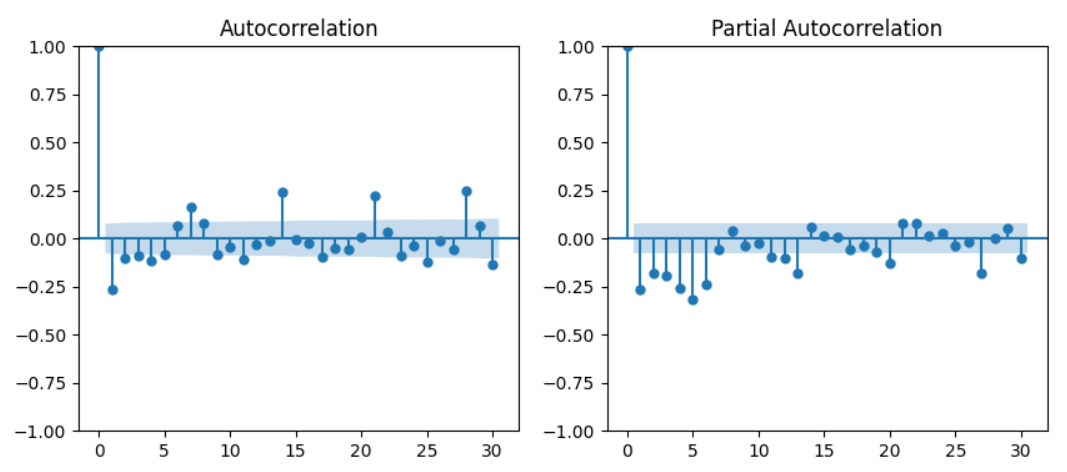
diff 변수의 ACF, PACF를 통해, 일반 차분값의 파라미터 p, d, q 값을 정할 수 있다. p, d, q란 ARIMA 모델을 학습시키기 위해서 필요한 값이다.

p: Auto Regressive 모델이 몇 lag 까지를 모델에 포함시킬 것인가
d: 차분을 몇번 적용할 것인가
q: Moving Average 모델이 몇 lag 까지를 모델에 포함시킬 것인가

아니, 선생님, Auto Regressive(AR), Moving Average(MA)는 또 뭡니까? 각각 자기 회귀, 이동 평균을 의미하는데, 간단히 설명하면, AR은 과거 시점의 데이터를 이용해 선형 회귀식을 만든다고 이해하면 될 것이다. MA는 선형 회귀식을 만들어서 그 식을 이용해 현 시점의 값을 예측해봤을 때, 실제값과의 오차로 또 선형 회귀식을 만든 것이다. ARMA는 이렇게 만들어진 두 식을 이어 붙인 개념이다. 아무튼, 이렇게 AR, MA 모델을 만드는 데에 참고할 과거 시점을 어디까지할지를 정하는 값이 바로 p, q 값인 것이다.

p값은 PACF 그래프를, q값은 ACF 그래프를 참고해서 정해볼 수 있는데, 이는 절대적인 기준이 아님을 유념하길 바란다. p값은 PACF 그래프에서 점이 처음으로 유의한 값이 아니라고 표시되는 시점, 즉, 그래프에서 블록 처리가 된 영역으로 값이 들어가기 직전의 시점을 기준으로 잡는다고 한다. 본 그래프에선 7을 p값으로 잡아볼 수 있을 것이다. q값은 ACF 그래프에서 y값이 '뚝' 떨어지는 시점을 기준으로 잡는다고 한다. 본 그래프에선 1을 q값으로 잡아볼 수 있을 것이다.

하지만 정상성을 띄는 그래프라면 으레 1시점부터 값이 마이너스로 떨어지기 마련이다. 마이너스로 떨어진 시점에서 '뭔가' 변화되는 포인트가 있다는 해석도 존재한다. 즉 p, q 둘 다 시점을 1 혹은 0으로 잡아야 한다는 것이다. 본 분석에선 둘 다 1로 잡고 분석을 진행해보기로 한다.

선생님, 그럼 d값은 어떻게 정하나요? 차분을 얼마나 진행했는지를 표시해주면 된다. 우리는 차분을 한 번 진행했으므로 d값은 1로 설정해주면 된다. 아니 선생님, 어차피 모델 만들 때는 차분을 한 번 진행한 데이터로 만드는 거 아닌가요? 아니다. 본 데이터인 cnt 데이터를 기준으로 만들어줄 것이기 때문에, d값은 1로 설정해주도록 하자!

계절 차분도 마찬가지 기준으로 해석을 진행하면 된다.

계절 차분을 통해 얻은 파라미터는 구분을 위해 대문자인 P, D, Q로 표기해준다. 이번엔 아까보다 뭔가 더 그럴싸한 느낌의 그래프이므로, P값은 2, Q값은 1로 보통의 해석 기준을 그대로 적용해주기로 한다. D의 경우 이번에도 역시 계절 차분 딱 한 번 진행해줬으므로 1로 표기해주자.

이렇게 p, d, q, P, D, Q 각각 1, 1, 1, 2, 1, 1이라는 값을 얻어줬다. 여기에 하나 더 파라미터가 필요한데, 바로 주기값이 그것이다. 우리 데이터에선 아까 구한 7을 사용해주면 되겠다.

  • SARIMA, AUTO_SARIMA

이렇게 구한 파라미터를 통해 이제 SARIMA 모델을 만들어보자.

from statsmodels.tsa.statespace.sarimax import SARIMAX

order = (1, 1, 1)
seasonal_order = (2, 1, 1, 7)

sarima_model = SARIMAX(
    train_df["cnt"],
    order=order,
    seasonal_order=seasonal_order
).fit()

SARIMA 모델을 자동으로 만들어주는 함수도 있다. 파라미터를 일종의 일종의 grid searching 방법으로 구해서 모델을 만드는 것이다.

from pmdarima import auto_arima

auto_sarima_model = auto_arima(
    train_df["cnt"],
    seasonal=True,
    m=7,
    D=1,
    trace=True
)

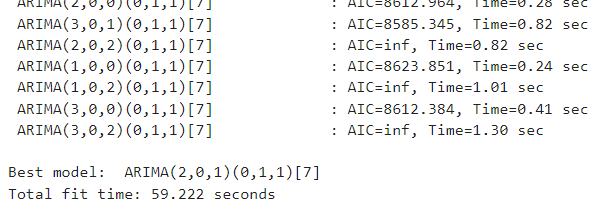
자동으로 구한 파라미터는 2, 0, 1, 0, 1, 1, 7인 것으로 나타났다. 우리가 직접 구한 파라미터와는 차이가 있을 건데, 이 말인 즉슨, 파라미터를 구함에 있어서 정확한 답은 없다는 것이다.

이렇게 만든 두 모델을 이용해 각각 예측값을 구하고, 실제값과 어느 정도 일치하는지 RMSE값을 비교해보도록 하자.

  • 모델 성능 확인
from sklearn.metrics import mean_squared_error

def calculate_rmse(df, label_column, target_column):
    target_df = df[[label_column, target_column]].dropna()
    rmse = mean_squared_error(
    	target_df[label_column], 
        target_df[target_column], 
        squared=False
        )
    print(f"{target_column} RMSE: {rmse}")

train_df["SARIMA"] = sarima_model.predict()
test_df["SARIMA"] = sarima_model.forecast(steps=len(test_df))
train_df["AUTO_SARIMA"] = auto_sarima_model.predict_in_sample()
test_df["AUTO_SARIMA"] = auto_sarima_model.predict(n_periods=len(test_df))

calculate_rmse(train_df, "cnt", "SARIMA")
calculate_rmse(train_df, "cnt", "AUTO_SARIMA")
calculate_rmse(test_df, "cnt", "SARIMA")
calculate_rmse(test_df, "cnt", "AUTO_SARIMA")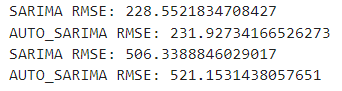

일단 성능 지표를 확인해보면 위 그림처럼 에러가 두 배 이상 늘어난 걸 확인할 수 있다. 이 문젠 잠시 제쳐두고, 수동 SARIMA와 자동 SARIMA 중 테스트세트 예측에 있어서 어느 쪽이 에러가 적은지 확인해보자. 수동 SARIMA가 에러가 더 적음을 알 수 있다. 즉, 자동으로 어떻게 구해냈다 해도, 그것이 반드시 더 좋은 성능을 내는 보장이 없다는 것이다. 그래도 결국 도토리 키재기일 뿐이다. 그래프로 그려보면 얼마나 현재 예측이 엉망인지 더욱 소상히 확인 가능하다.

from matplotlib import pyplot as plt

test_df[["cnt", "SARIMA", 'AUTO_SARIMA']].plot(figsize=(10, 3))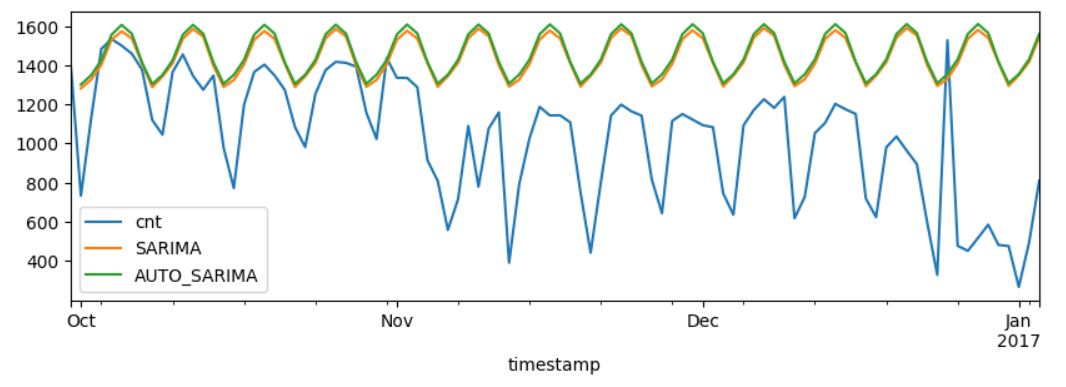

거의 OMR 카드에다 자 대고 한 줄로 쫙 그은 수준이다. 아니 그럼 선생님, 이제 우린 어떻게 해야한다 말인가요? 아직 한 발이 남았다. 바로, 외생 변수를 삽입하여 만드는 SARIMAX 모델을 만들어보는 것이다.

3. SARIMAX

외생 변수를 삽입하지 않은 경우 SARIMA는 모든 날들에 동일한 가치를 부여한다. 분명 주말/휴일 여부에 따라, 계절에 따라, 날씨에 따라 소비 패턴에 차이가 있을 건데 말이다. 그래서 이런 요소들을 고려하라고 알려준다면, 그 모델은 좀 더 정확한 예측을 해내지 않을까? 바로 이런 요소들을 외생 변수라고 하며, 외생 변수를 고려한 SARIMA 모델을 SARIMAX라고 한다.
SARIMAX 모델은 코드만 살짝 다르고 자동으로 파라미터는 추출해주지만 모델까지 만들어주진 못하는 것 말곤 SARIMA 모델과 크게 다르지 않다.

from statsmodels.tsa.statespace.sarimax import SARIMAX

exog = train_df.columns[1:15]

sarimax_model = SARIMAX(
    train_df["cnt"],
    exog=train_df[exog],
    order=order,
    seasonal_order=seasonal_order
).fit()

train_df["SARIMAX"] = sarimax_model.predict(
	exog=train_df[exog]
)

test_df["SARIMAX"] = sarimax_model.forecast(
	steps=len(test_df), 
    exog=test_df[exog]
)

아까 구해놓은 파라미터를 그대로 이용해주고 여기에 외생 변수만 넣어주면 된다. 외생 변수로는 종속 변수 cnt를 제외한 나머지 모든 변수들을 사용해주자.

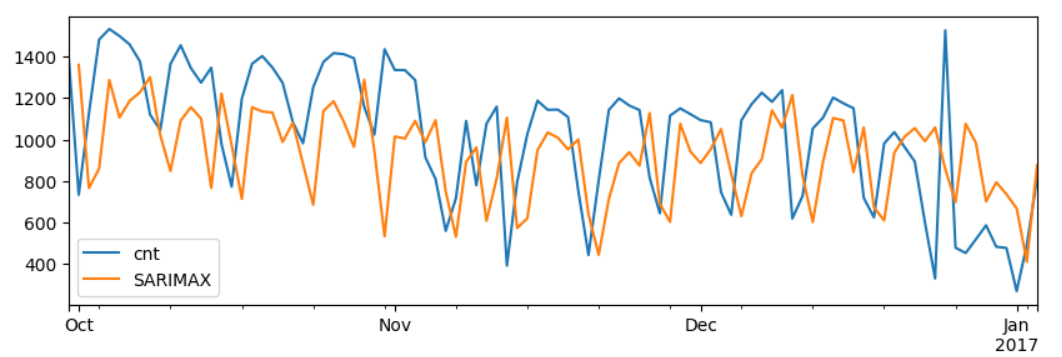
일단 그래프만 대충 딱 봐도, 예측이 훨씬 정교해졌음을 알 수 있다. SARIMA에 비해 에러가 훨씬 줄었다. 여기서 얼추 몇 시점만 앞으로 땡겨주면 매우 훌륭한 적합도를 보일 것 같다.

4. Prophet

지금까지 우리는 시계열 데이터의 속성을 파악하여 수동으로든 자동으로든 파라미터를 구해서 하나하나 가장 적합한 모델이 뭔지 직접 비교해가는 과정을 거쳤다. 하지만 Meta에서 개발한 Prophet 모델을 사용하면, 이런 과정을 모두 생략하면서도 훨씬 정교한 모델을 만들어낼 수 있다.

import pandas as pd
from prophet import Prophet
from prophet.plot import plot_plotly

df = pd.read_csv(
	"./data/london_bike.csv", 
    index_col='timestamp', 
    parse_dates=True
)
df1 = df.iloc[:, :5].resample('D').mean()

def most_common(x):
    if x.empty:  # 그룹이 비어있는 경우 처리
        return None
    return x.value_counts().idxmax()

df2 = df.iloc[:, 5:].resample('D').apply(most_common)

df1 = df1.interpolate(method='time')
df2 = df2.interpolate(method='time')

df = pd.concat([df1, df2], axis=1)

threshold = pd.Timestamp("2016-09-30")
threshold2 = pd.Timestamp("2016-10-01")
train_df = df[:threshold].copy()
test_df = df[threshold2:].copy()

train_df['weather_code'] = train_df['weather_code'].astype(str)
train_df['season'] = train_df['season'].astype(str)
test_df['weather_code'] = test_df['weather_code'].astype(str)
test_df['season'] = test_df['season'].astype(str)

train_df = pd.get_dummies(train_df, drop_first=True)
test_df = pd.get_dummies(test_df, drop_first=True)
>
# test셋엔 'weather_code_26.0', 'season_1.0', 'season_2.0' 범주가 없음.
test_df[['weather_code_26.0', 'season_1.0', 'season_2.0']] = 0
test_df = test_df[train_df.columns]

# 인덱스 설정 된 변수를 인덱스 해제
train_df = train_df.reset_index()
test_df = test_df.reset_index()

# 시간 정보를 담고 있는 변수는 'ds'로, 종속 변수는 'y'로 칼럼명 변경
train_df = train_df.rename(columns={"timestamp": "ds", "cnt": "y"})
test_df = test_df.rename(columns={"timestamp": "ds", "cnt": "y"})

# Prophet 모델 생성
prophet_model = Prophet()

# 모델에 외생 변수 추가
for col in train_df.columns[2:]:
    prophet_model.add_regressor(col)

# 모델 학습
prophet_model.fit(train_df)

# 미래 예측을 위한 데이터프레임 생성
future = prophet_model.make_future_dataframe(
	periods=len(test_df), 
    freq='D'
)

for col in train_df.columns[2:]:
    future[col] = pd.concat(
    	[train_df[col], test_df[col]],
        axis=0
    ).reset_index(drop=True)

# 예측 수행
forecast = prophet_model.predict(future)

# 그래프 생성
plot_plotly(prophet_model, forecast)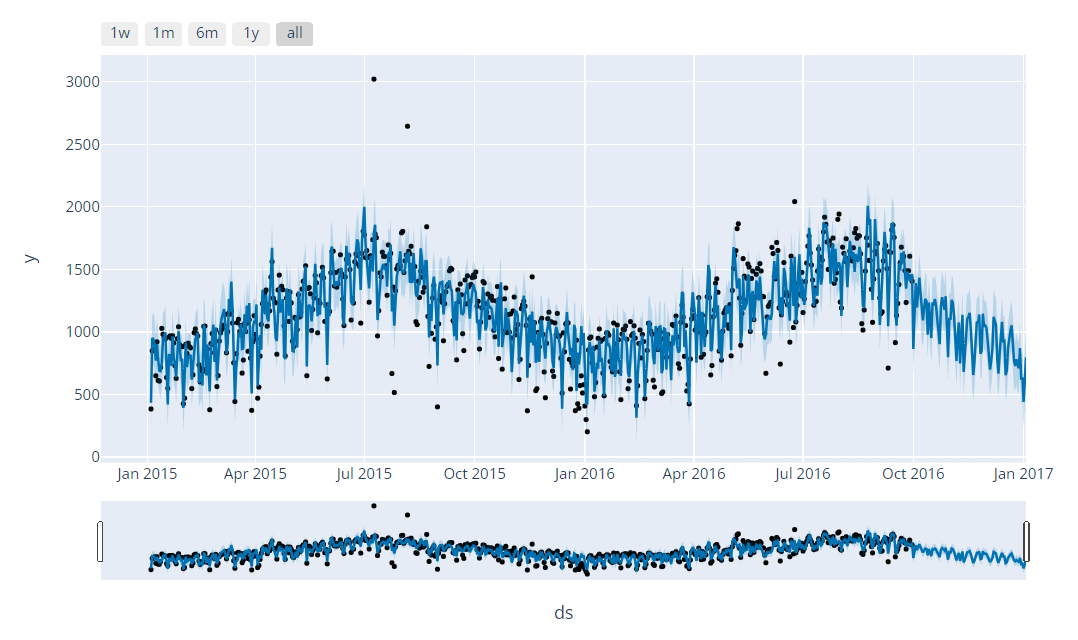

그래프를 보면 검은 점들이 실제값들이 파란 선은 그에 대한 예측을 해내는 선이다. Prophet에서 설정해줄 파라미터는 freq, 즉, 시점 간격밖에 없다. 이거 하나만 설정해주면 이렇게 인터엑티브한 그래프를 만들어줄 수 있다. 그럼, 실제 예측해내는 정도는 어느 정도 수준일까? 

from sklearn.metrics import mean_squared_error

forecast1 = forecast.set_index("ds")
test_df1 = test_df.set_index('ds').join(forecast1["yhat"])
test_df1[['y', 'yhat']].plot(figsize=(10, 3))

rmse = mean_squared_error(test_df1["y"], test_df1["yhat"], squared=False)
print(f"RMSE: {rmse}")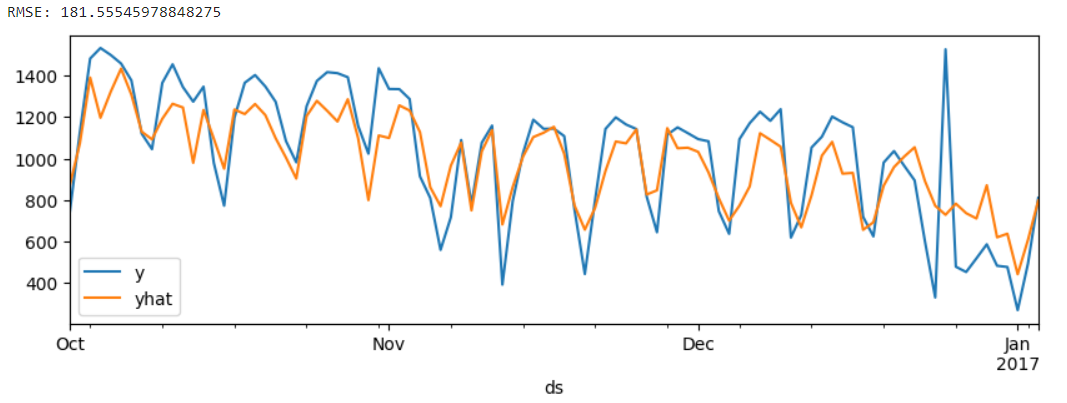

Prophet test 모델 적합도가 SARIMAX로 train 모델 적합했을 때와 비슷한 수준으로 나온다. 이 얼마나 굉장하고 허무한 결과인가. 이런 편의성과 성능적 우수함 덕분인지 현업에선 Prophet 모델을 많이 이용한다고 한다.

5. 마치며

시계열 데이터 분석을 한다 하면, 우선, 계절성이 있는지 없는지 판단하고, 외생 변수를 추가한 ARIMAX 혹은 SARIMAX 모델을 만들어준다면 꽤나 우수한 예측 모델을 만들 수 있다. 그러나, 이들의 성능을 가뿐히 뛰어넘는 Prophet 모델을 사용하는 게 현장에선 마음이 한결 가벼울 것 같다. 편의성, 성능적 우수함 뿐만 아니라 실제로는 시계열 이론 틀이 잘 적합하는 데이터가 잘 없다고 하니, 이론적 근거를 바탕으로 만들어가는 ARIMA 모델이 힘을 발휘하긴 어려운 환경이기도 하니 말이다.

profile
수수
반갑구만 반가워요
이전 포스트

코로나와 주식, 그리고 Granger Test

다음 포스트

넌 고양이니 개니?

0개의 댓글