그룹 비교: 통계 검정
6.1 그룹 비교를 위한 데이터
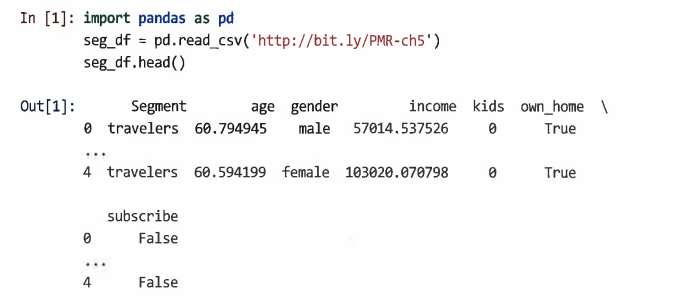
- 앞선 5장의 데이터를 그대로 사용한다.
6.2 그룹 빈도 검정:scipy.stats.chisquare()
- 그룹 간의 차이가 실제 유의미한 차이인지를 식별하기 위해서 통계 검정을 진행해야 한다!
- 카이제곱 검정은 가장 간단한 통계 검정 중 하나로, 2개의 범주형 변수가 서로 연관성이 있는지, 즉 서로 독립인지를 통계적으로 판단하는 방법이다.
H0(귀무가설): 두 변수 사이에 확률적으로 차이가 없다.
H1(대립가설): 두 변수 사이에 확률적으로 차이가 있다. - 카이제곱 검정은 셀의 빈도가 총 개수를 기준으로 예상되는 것과 크게 다른지 여부를 결정한다.
- Scipy stats에서 chisquare() 명령을 사용해 카이제곱 검정을 실행할 수 있다.
예1) 데이터가 0에서 3까지의 숫자에 대한 95개의 관측치를 포함하고 각각의 개수는 거의 같지만 완전히 동일하지는 않다. scipy.stats.chisquare()로 이를 검정한다.
-
데이터 생성

-
Numpy의 unique() 메서드를 사용해 각 값의 개수를 얻는다.

-
Scipy에서 stats를 임포트하고 stats.chisquare() 메서드를 사용한다.

-
N = 95의 관측치 개수가 주어졌을 때 0, 1, 2, 3 값이 균등하게 분포된 대규모 모집단에서 데이터가 무작위로 샘플링됐다는 귀무가설하에 이러한 결과가 나타날 가능성을 평가할 수 있다.
-
0.852의 p값은 귀무가설이 참인 경우 테이블에 있는 것과 유사하거나 더 큰 차이가 있는 데이터셋을 볼 확률이 85%로 추정됨을 나타낸다. 즉, 네 숫자의 실제 빈도 차이가 있지 않다.
-
이 데이터는 무작위 표본 추출을 가정할 때 모집단의 그룹 크기가 동일하지 않다는 증거를 보여주지 못한다.
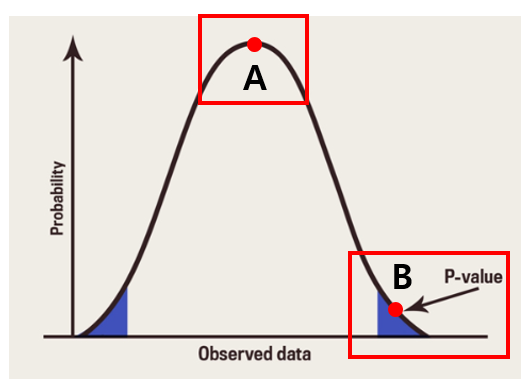
* p값(p-value)
어떤 사건이 우연히 발생할 확률, 유의확률
- A의 경우 우연히 관측될 확률이 높다.
- B의 경우 우연히 관측될 확률이 낮다.
- 즉, 우연히 일어날 확률, 유의확률이 작을수록 해당 사건은 무언가의 이유(인과관계, 상관관계 등)이 있을 것이라고 추측할 수 있다.
- 보통 p값이 0.01이나 0.05보다 작을 경우 귀무가설을 기각한다.
예2) 위의 코드에서 관측치 개수 '3'을 20부터 10까지 변경할 경우

- 이 경우 p값은 0.047이므로 '95% 신뢰도'로 숫자 간에 차이가 없다는 귀무가설을 기각할 수 있다고 결론 내릴 수 있다.
- 즉, N = 85개 관측치의 무작위 표본이라고 가정할 때 현재의 0부터 3 사이의 값 분포는 더 큰 모집단에서는 같지 않을 가능성이 있음을 시사한다.
예3) 위의 코드에서 표본이 더 작을 경우
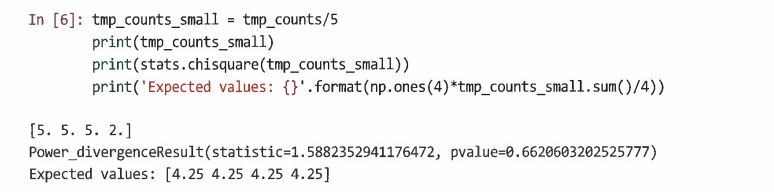
- '3'그룹의 사람들 비율은 결과가 유의한 것으로 나왔던 앞선 더 큰 표본과 동일하지만 여기서는 p값이 유의하지 않다는 결과를 보여준다.
- 결과는 실제 효과뿐 아니라 표본 크기에 따라서도 달라질 수 있다!
- 일반적으로 카이제곱 검정에 필요한 표본의 크기는 전체적으로 20보다 크고 각 카테고리는 5보다 커야한다.
예4) 위의 코드에서 표본이 더 클 경우
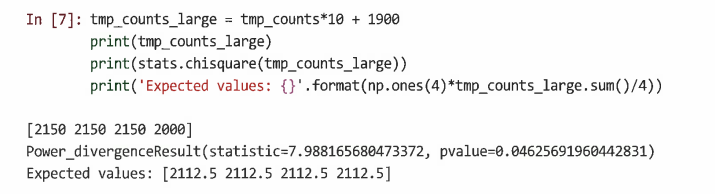
- 여기서 p값은 0.05보다 작은 것으로 나오지만 표본의 크기가 크면 그룹 간의 비례 차이가 상대적으로 작더라도 그렇게 나온다.
- 이 경우 비즈니스 문맥이 중요하다. '3'그룹은 예상보다 약 100명의 회원이 적으며, 이것이 통계적으로 유의미함에도 중요한 것인지 판단할 수 있어야 한다.
- 종종 큰 숫자의 경우 통계적 유의성은 그다지 중요하지 않으며, 차이의 크기를 추정하는 효과 크기(effect size)를 사용하는 것이 더 유용할 수 있다.
예5) N = 300 관측치가 있는 시뮬레이션 세크먼트 데이터에서 세그먼트 크기가 서로 다른지 알아보자
-
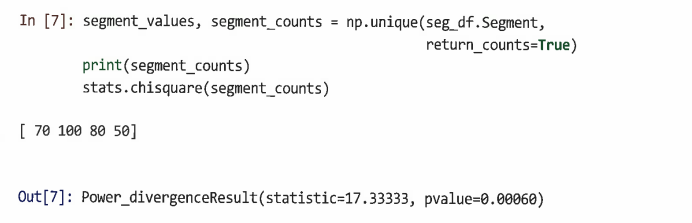
이 데이터의 경우 데이터프레임 형태이기 때문에 np.unique() 대신 pandas의 value_counts() 메서드도 사용할 수 있다.
-
p값이 0.00060으로 세그먼트 크기에 차이가 있다.
-
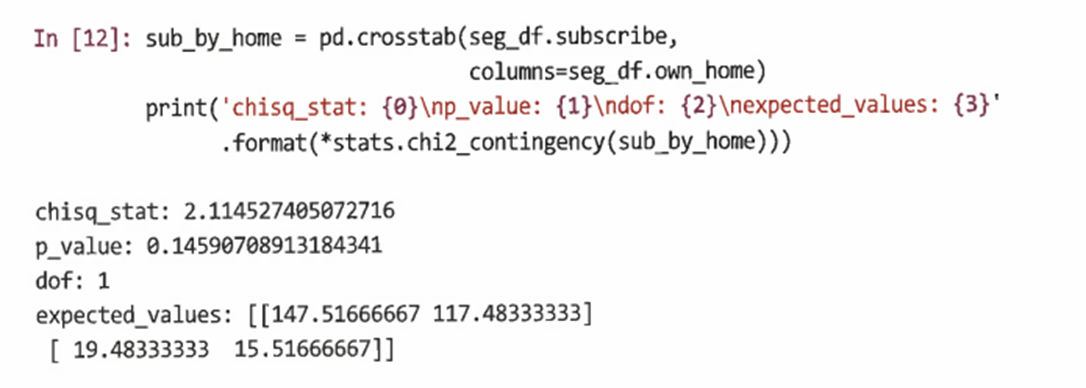
데이터를 추출할 때 가정한 것처럼 구독 상태는 주택 소유와 무관하기 때문에 응답자는 주택 소유 상태와 관계없이 구독할 가능성이 동일하다. pandas의 crosstab() 메서드를 사용해 양방향 테이블을 생성하고 chisquare_contingency()를 사용해 검정할 수 있다.
-
이 경우 귀무가설을 숫자의 개수가 한계 비율에서 예상할 수 있는 것과 같다는 것이다.
-
p값에 따라 귀무가설은 기각되며, 주택 소유가 구독 상태와 무관하다는 증거가 없다는 결론을 도출할 수 있다.
6.3 관찰된 비율 검정: binom_test()
예1) 2014년 슈퍼볼 경기일에 맨해튼에서 12개의 시애틀 팬 그룹과 8개의 덴버 팬 그룹을 관찰했다. 관찰값은 이항값의 무작위 표본이라고 가정할 때, 관찰된 시애틀 팬이 60%이었다면, 이는 팬들이 서로 동일(각각 50%)하다는 가정으로부터 유의하게 다른 것인가?

- statsmodels.proportion.binom_test()를 사용해 참 가능성이 50%라면 20개 중 12개를 무작위로 관찰할 가능성을 단방향으로 검정한다.
- p값은 유의하지 않다. 즉, 귀무가설 채택.

- 95% 신뢰구간을 살펴보면 95% 신뢰구간은 36~81%이며, 이는 귀무가설 값인 50%를 포함한다. 따라서 20명의 표본에서 60%의 시애틀 팬을 관찰했다는 사실은 뉴욕을 걸어다니는 더 큰 그룹에는 시애틀 팬이 더 많이 포함됐다는 사실을 확실히 증명하지 못한다.
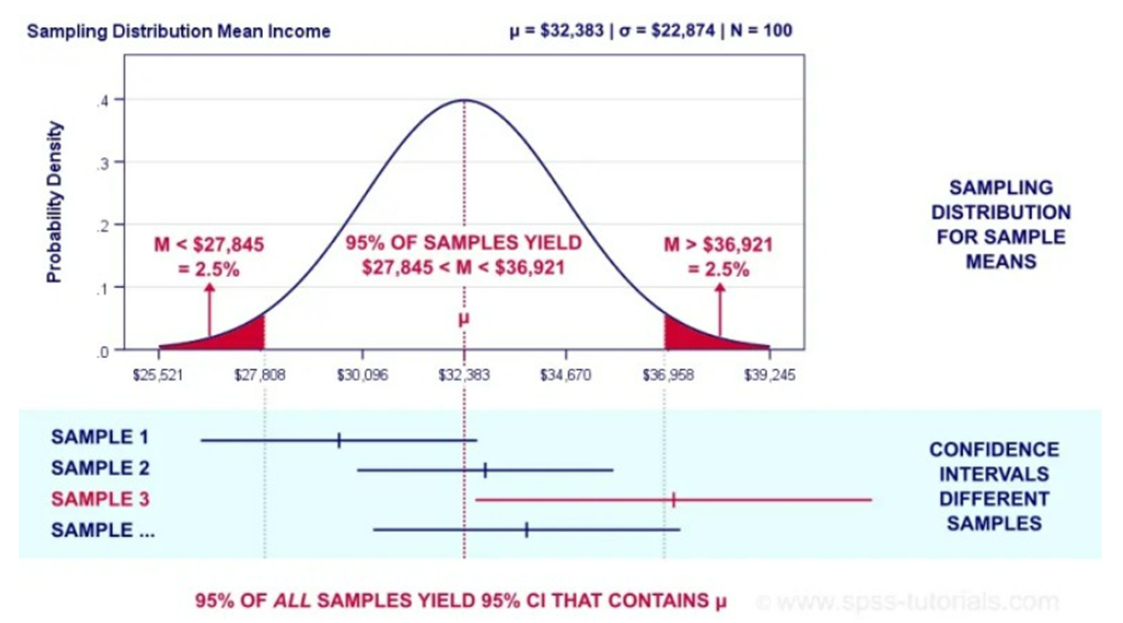
6.3.1 신뢰 구간 정보
95% 신뢰구간: 표본 변화에 따라 변하는 신뢰구간 중에서 약 95%는 모평균을 포함한다는 의미
- 참 값이 신뢰구간 범위에 있다는 의미가 아닌, 실제 값이 우리가 얻은 값이라면, 무작위 샘플링의 추가 라운드에서 추가 추정치가 이 신뢰구간 95% 이내에 속할 것으로 예상하는 것!
=> 신뢰구간은 참 값이 아니라 추정치에 관한 것.
- 신뢰구간에서 귀무가설이 제외되면 결과는 통계적으로 유의하다고 한다.
6.3.2 binom_test()와 이항 분포에 대한 추가 정보
예2) 위의 예시와 같은 비율이지만 더 큰 샘플로 200명 중 120명이 시애틀 팬이라고 관찰됐다면?
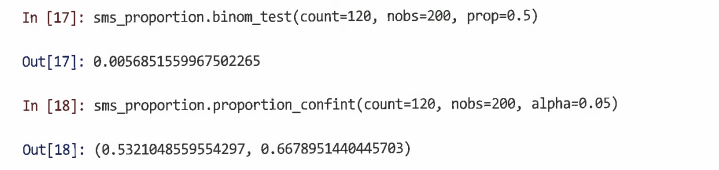
- 이 경우 신뢰구간에 더 이상 50%가 포함되지 않는다.
- p값은 0.05보다 작으며 통계적으로 유의한 차이를 나타낸다.
예3) 실제 비율이 50%인 경우 20명 중 8~12명의 시애틀 팬을 관찰할 확률은 얼마일까?

- 리스트에 각 예상 숫자 지정하거나, range() 사용해 리스트 생성하는 두 가지 방법 존재.
- Scipy의 stats.binom을 사용해 관심 범위에 걸친 이항 분포에 대한 밀도 추정값을 사용하고 포인트 확률을 합산한다.
- 20명의 팬을 관찰한 경우 만약 참 분할이 50%였다면 8~12명의 팬을 관찰할 확률은 73.7%이다.

- 정확한 이항 검정은 신뢰 구간을 추정하는데 지나치게 보수적일 수 있다. 아그레스티-쿨 방법을 사용하면 신뢰 구간이 약간 더 작지만 여전히 50%를 포함한다.

- 이를 이용해 시애틀과 덴버 팬이 혼합된 그룹이 구성될 가장 가능성 있는 비율도 도출할 수 있다.
- 관찰된 혼합 그룹은 20개 중 0개였지만, 혼합된 팬 그룹의 발생은 0~19% 사이에 있을 가능성이 높다.
6.4 그룹 평균 검정: t-검정
t-검정: 한 표본의 평균을 다른 표본의 평균과 비교한다. 정확히 두 집합의 데이터 평균을 비교하여 통계적으로 유의한 차이가 있나 검증.
- p-값이 0.05보다 작으면 통계적으로 유의미한 차이가 있는 것으로 본다.
- 통계 검정이나 모델을 적용하기 전에 데이터를 조사하고 왜도, 불연송성, 특이값을 확인하는 것이 중요하다.
=> 히스토그램 또는 QQ그림으로 비정규 분포를 확인할 수 있다. - 많은 통계 검정에서는 데이터가 정규 분포나 다른 부드러운 연속 분포를 따른다고 가정하기 때문에 이러한 가정을 위반하는 왜도나 특이값을 주의할 필요가 있다.
예1) 응답 변수인 income을 설명 변수인 own_home으로 설명할 수 있는지 측정
-
먼저 데이터에 대한 표본 평균과 표준 편차 확인

-
t-test 통해 주택 소유가 전체 부문에서 소득 차이와 관련이 있는지 여부 검정

=> t통계가 -3.96이고 p값이 0.00009임을 알 수 있다. 즉, 주택 소유에 따른 소득 차이가 없다는 귀무가설이 기각된다. -
주택 소유자와 비소유자 간 평균 소득 차이의 95% 신뢰 구간 확인

-
stats.t.interval(alpha간격너비 , df자유도, loc그룹a와 b의 평균 차이, scale각 그룹에 대한 표준 오차의 기하 평균) 사용.
-
95% 신뢰구간이 -11525~-5514로, 이 표본이 더 큰 모집단의 대표적인 데이터였다면 반복 샘플링에서 그룹 차이가 해당 값 사이에 있을 것임을 95% 신뢰할 수 있다.
예2) 마찬가지로 Travelers 세그먼트의 차이점을 측정

-
-6107~7054의 신뢰구간은 0을 포함하므로 p값 0.93에서 제시된 바와 같이 집을 소유한 여행자와 그렇지 않은 여행자 간의 평균 소득에 유의한 차이가 없다는 결론이 나온다.
=> 예1의 t-검정과 달리 Travelers 내에서는 주택 소유에 대한 소득에 유의미한 차이가 없음을 확인했다. 즉, 차이점은 대부분 Travelers 그룹 외부에 있어야 한다. -
t-검정은 두 그룹만 비교하기 때문에 4개의 세그먼트에 대한 t-검정은 작동하지 않는다. 따라서 이 경우 분산 분석을 진행해야 할 필요가 있다.
6.5 다중 그룹 평균 검정: 분산 분석(ANOVA)
6.5.1 수식 구문에 대한 간략한 소개
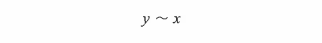
- 물결을 기준으로 왼쪽은 응답 변수, 오른쪽은 설명 변수.
6.5.2 분산 분석
- 분산 분석: 여러 그룹의 평균을 비교한다. 각 그룹의 분산이 비슷하다고 가정한 상태에서 여러 평균 간의 차이를 검정한다.
예1) 세그먼트 데이터의 평균 소득 차이, 특히 주택 소유나 세그먼트 멤버십 또는 둘 다와 관련된 소득에 관해 알아본다

- Scipy의 stats 안에 있는 일원 분산 분석 메서드인 f_oneway()를 사용하며, 다수의 배열이 주어지면 F값과 연계된 p값을 반환한다.

- stats.anova 모듈을 통해 좀 더 완전한 기능을 갖춘 ANOVA 메서드 집합을 사용할 수 있다.
- statsmodels.formula.api.smf.ols(formula, data)를 사용함으로써 모델과 statsmodel.stats를 설정하고 표준 ANOVA 요약을 표시한다.
- 여기서는 주택 소유에 따른 소득을 확인할 수 있다.
=> PR(>F)값은 p값이며, 자신의 주택을 소유한 사람과 소유하지 않은 사람 사이에 유의한 소득 차이가 있음을 반영한다.

- 동일한 방법으로 부분별 소득을 확인할 수 있다.
=> PR(>F)값은 0에 매우 가까워 소득이 부문별로 유의하게 다르다는 것을 확인한다.

- 소득과 주택 소유 두 요소를 모두 추가할 수도 있다.
=> Segment와 own_home 둘 다에서의 소득 차이를 설명하려고 할 때 세그먼트는 유의한 예측 변수이지만 주택 소유는 유의한 예측 변수가 아님을 나타낸다. 이는 이전 결과와 차이를 보이는데, 그 이유는 현재로서는 세그먼트와 주택 소유권이 독립적이지 않고 세그먼트 멤버십만으로도 효과가 충분히 포착된다는 것이다.

- 주택 소유가 일부 세그먼트에서는 소득과 관련이 있지만 다른 곳에서는 관련이 없을 수 있다. 이는 모델에서 상호 작용 효과로 표현된다.
- 모델 공식에서 '+'는 주 효과, ':'는 상호작용, '*'는 주 효과와 상호 작용을 나타낸다.
=> 세그먼트는 중요한 예측 변수이나, 주택 소유권과 세그먼트의 상호 작용은 유의하지 않음을 확인할 수 있다.
6.5.3 ANOVA에서 모델 비교
-
anova_lm(model1, model2, ...) 구문을 사용해 2개 이상의 모델을 비교할 수 있으며, 세그먼트만 있는 ols() 모델과 세그먼트와 수입이 모두 있는 모델을 비교할 수 있다.
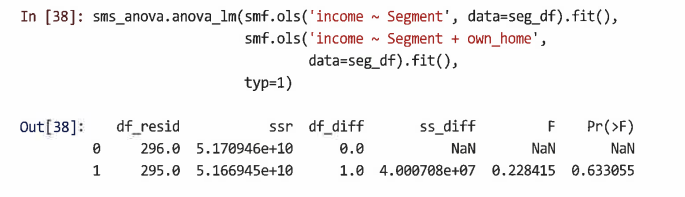
=> 이는 세그먼트와 주택 소유권을 모두 포함하는 모델 1이 모델 0과 전체적으로 크게 다르지 않다는 것을 의미한다. -
anova_lm() 명령으로 수행되는 모델 비교는 중첩된 모델의 경우에만 의미가 있다는 점에 유의해야 한다.
6.5.4 그룹 신뢰 구간 시각화
-
기본 ols() 모델에는 절편항이 있고, 다른 모든 세그먼트는 이에 상대적이다.
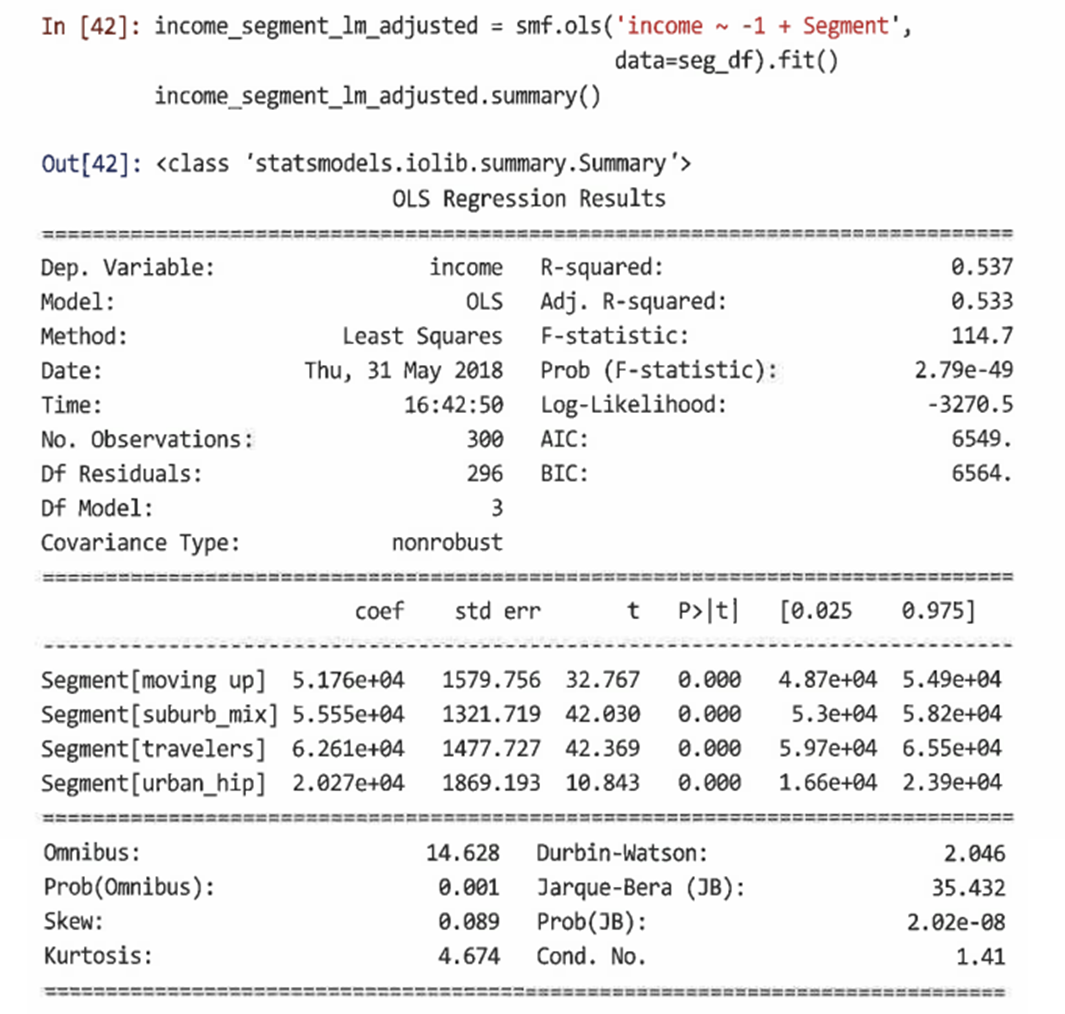
-
모델 공식에 '-1'을 추가해 절편을 제거하는 것이 좋다. 절편이 제거되는 각 계수는 각 세그먼트의 평균 수입에 해당한다.

-
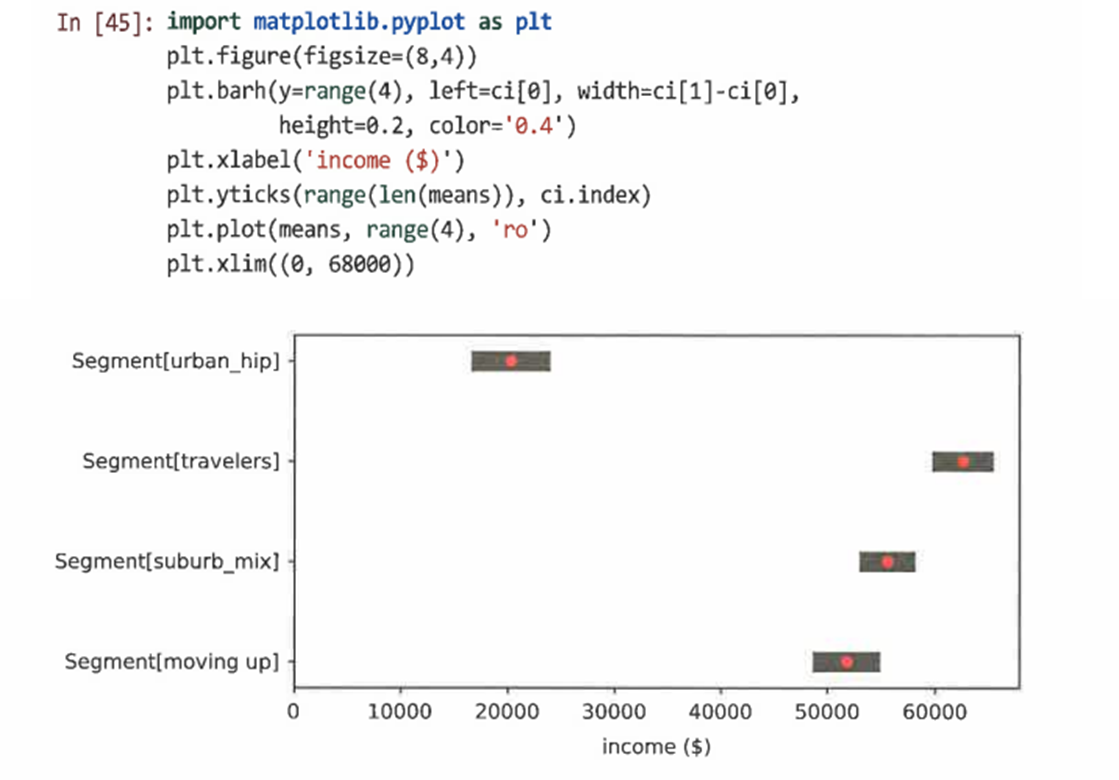
다음과 같이 모델의 평균과 신뢰구간을 그릴 수 있다.
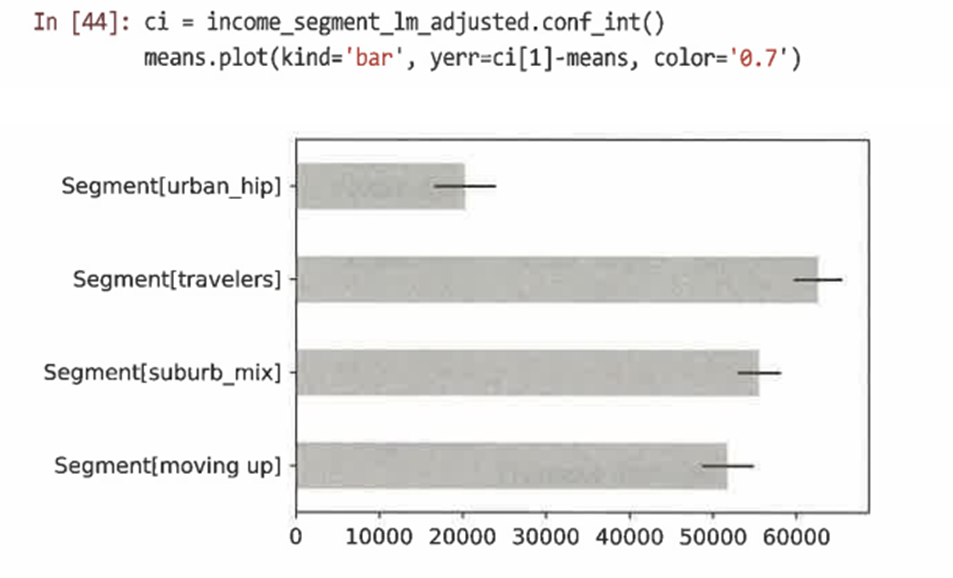
-
다음과 같이 각 세그먼트의 평균 수입에 대한 신뢰구간을 볼 수 있다.
6.6 요점