결과의 동인 식별: 선형 모델

• 만족 동인 분석: 제품의 특정 요소 및 그 제공과 관련해 제품에 대한 만족도를 모델링하는 것
• 마케팅 믹스 모델링: 가격과 광고가 판매와 어떻게 관련돼 있는지 이해하는데 사용되는 선형 모델
• 이때, 동인은 인과 관계를 암시하지 않으며, 모델은 변수 간의 연관성을 나타낸다.

7.1 놀이공원 데이터

• 데이터셋 생성
  

7.1.1 놀이공원 데이터 시뮬레이션

• 랜덤 시드 설정해 관측치에 대한 변수 선언
  

• 각 만족도 점수에 영향을 끼치는 고객의 무작위 변수인 halo로 만족도 후광 점수를 시뮬레이션한다.
  

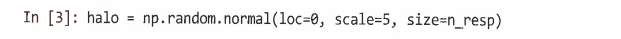
• 설문 조사 항목에 각 응답자의 후광 점수를 추가해 만족도 평가에 대한 응답을 생성한다. 이때 floor()를 사용해 연속값을 정수로 변환한다. 그런 다음 해당 범위를 벗어난 값을 대체해 값을 0-100 범위로 제한한다.
  

• 다른 영향에 대한 가중치 기여도를 추가한다.
  

• random.normal()을 사용해 임의의 정규 변형을 추가한다.
  

• 데이터 포인트를 데이터프레임으로 결합한다.
  

7.2 ols()로 선형 모델 적합화하기

• describe() 이용해 데이터 검사
  

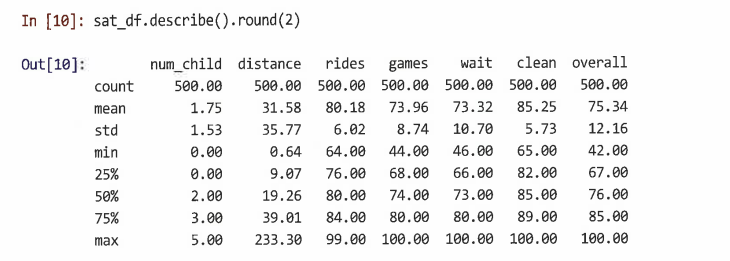
7.2.1 예비 데이터 검사

• 모델링하기 전 확인해야 할 두 가지 중요한 사항:

1. 각 개별 변수가 합리적인 분포를 갖고 있는지
2. 변수 간의 공동 관계가 모델링에 적합한지 확인

• seaborn.PairGrid()를 사용해 sat_df의 변수 분포 및 관계에 대한 초기 검사 수행
  
  => 이항인 weekend와 고도로 치우친 분포를 가진 distance를 제외하고 모든 만족도 등급이 정규 분포에 가깝다는 것을 알 수 있다.

• 로그 변환을 통해 좀 더 정규 분포로 변환한다.
  

=> 그림 7.1 우중앙에 있는 변수가 양의 상관관계가 있는 것으로 보인다는 사실에 주의!

• 만족도 조사의 경우 응답자들은 각 항목에 대해 독립적으로 평가하지 않았을 수 있다.

• 그러나 변수가 강하게 연관되어 있으면 통계 모델로 개별 효과를 평가하기 어렵다.

• pandas의 corr()과 sns.heatmap()을 사용해 상관관계 구조를 추가로 조사한다.
  
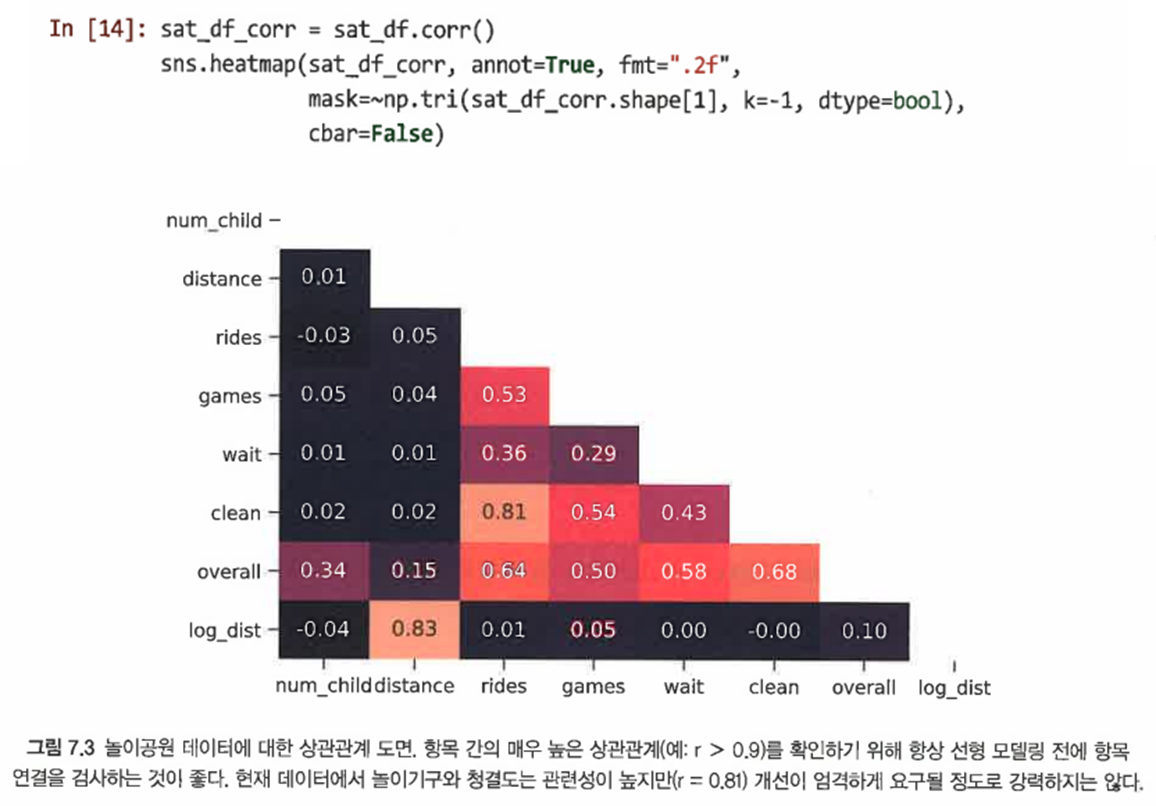
  => 여러 항목에 대해 상관관계가 매우 강해 문제가 되는 것은 없는 것으로 보이기 때문에 이대로 선형 모델링을 진행해도 괜찮은 것으로 평가된다.

7.2.2 요약: 이변량 연관성

• 상관관계가 약한지, 강한지 판단하기 위해 두 변수를 서로에 대해 도식화할 수 있다.
  
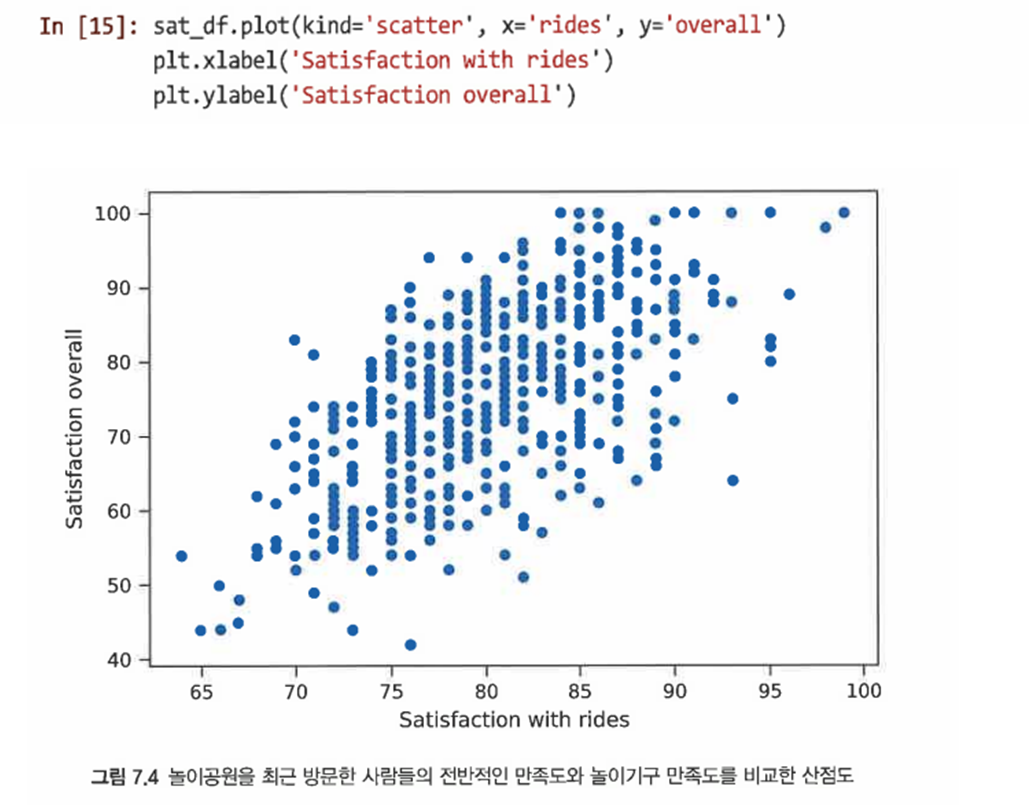
  => 놀이기구에 대한 만족도가 높은 사람들의 전반적인 만족도도 더 높은 경향이 있음을 알 수 있다.

7.2.3 단일 예측자가 있는 선형 모델

• 전체적인 만족도와 놀이기구 만족도에 관련된 선형 모델을 추정하기 위해 overall~rides 공식을 사용하며, 이는 'overall은 rides에 따라 변함'으로 읽을 수 있다.
  
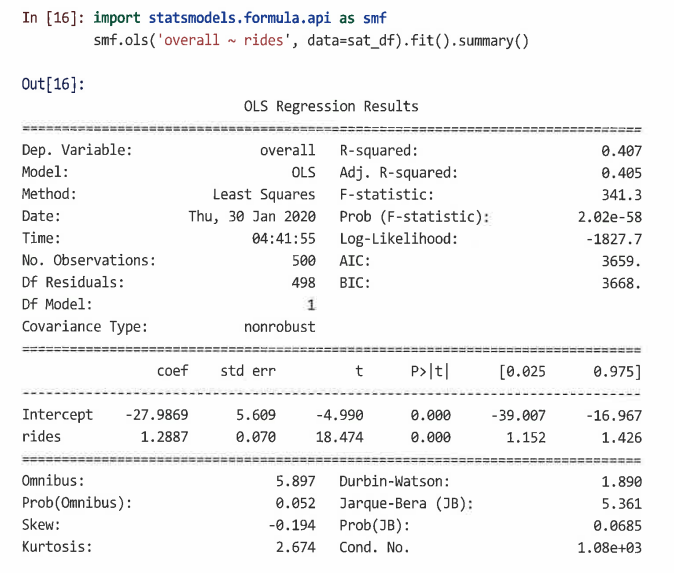
  => 가장 중요한 부분은 coef 열의 모델 계수를 보여주는 중간 부분이다. rides의 계수는 1.2887이므로 rides에 대한 각 추가 평가 점수는 overall 점수를 1.2887점 증가시키는 것으로 추정된다.
  => std err 열은 데이터가 더 큰 모집단의 무작위 표본이라는 가정하에 계수 추정치의 불확실성을 나타낸다.
  => t값, p값과 신뢰구간은 계수가 0과 유의하게 다른지 여부를 나타낸다.

• 절편과 계수는 rides 값에 기반해 응답자의 overall 보고서에 대한 최상의 추정치를 결정하는데 사용할 수 있다.

7.2.4 ols 객체

• 모델에 기반해 overall을 추정하기 위해 ols 객체의 predict() 메서드를 사용할 수 있다.
  

• 위와 마찬가지로 overall~rides에 대한 산점도를 다시 그리면 모델 예측을 사용해 선형 적합선을 추가할 수 있다.
  

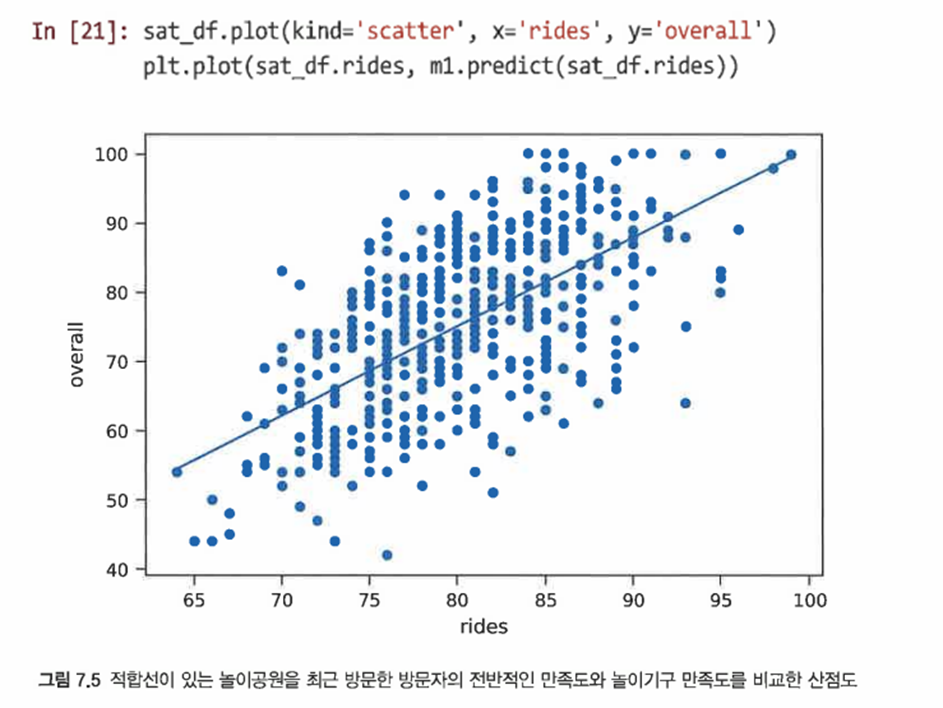
• 또한 잔차를 검사할 수 있다.
  
  => 잔차의 범위는 -27.954에서 22.757까지 매우 넓으며, 이는 주어진 데이터 포인트에 대해 예측이 다소 틀릴 수 있음을 의미한다.

• 히스토그램을 그려 잔차의 대칭을 확인해볼 수 있다.
  
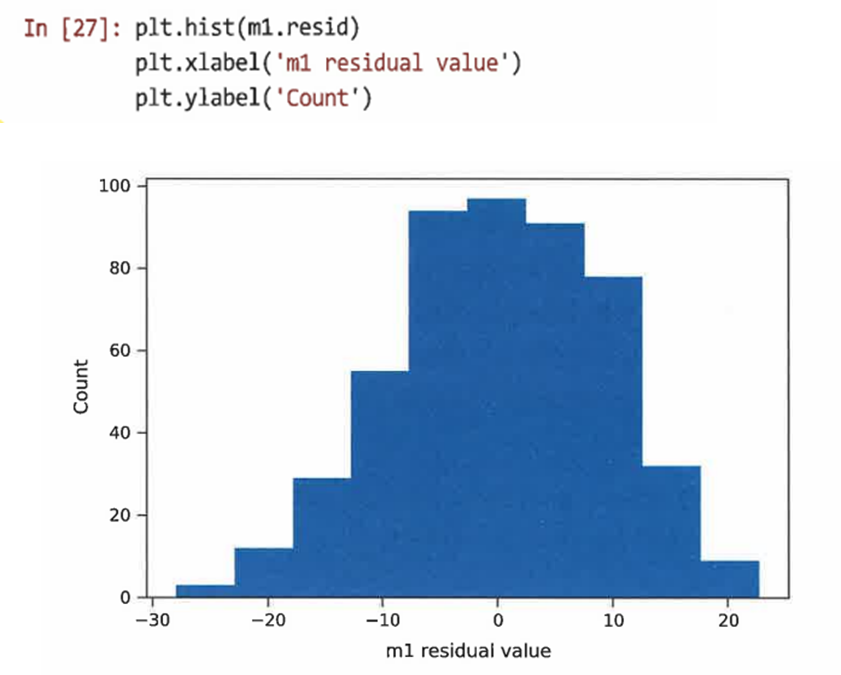
  => 히스토그램이 대칭에 가깝다는 것은 모델이 편향되지 않았다는 좋은 신호이다.

7.2.5 모델 적합 확인

• 선형 모델을 데이터에 적합화할 때:
  가정1. 예측 변수와 결과 간의 관계가 선형이다.
  y가 x^2의 함수인 데이터를 생성한 다음 선형 모델 y~x에 적합화하면 곡선인 점 구름들 사이를 통과하는 직선이 그려진다.
  
  => x에 대한 적합계수는 -0.1129이고 t-검정은 계수가 0과 유의하게 다르지 않다는 것을 보여준다.

• x대 y를 도식화한 다음 도면에 적합선을 그리면 무슨 일이 일어나고 있는지 더 명확하게 볼 수 있다.
  

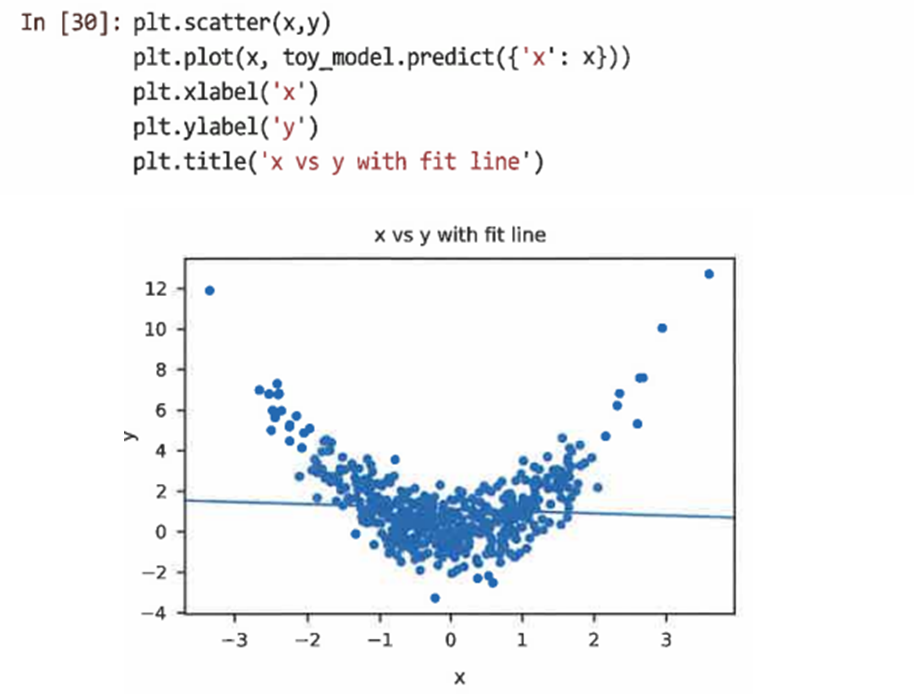
가정2. 예측 오차가 정규 분포를 따르고 패턴이 없는 랜덤 노이즈처럼 보인다는 것이다.
모델의 적합화 값 대 잔차를 그려 조사한다.

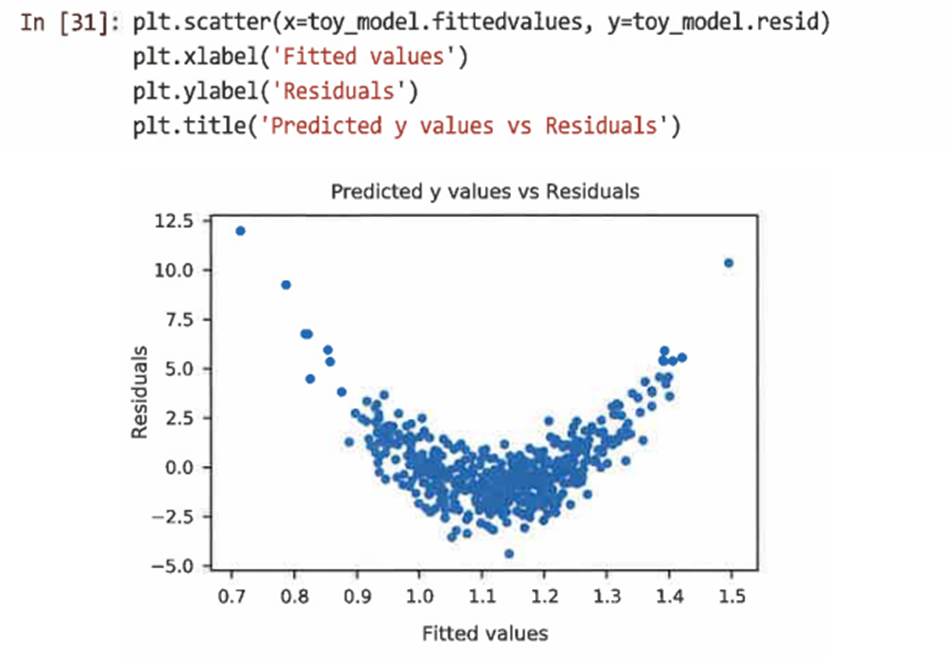
=> 0에 가까운 y의 값을 과소 예측하고 0에서 멀리 떨어진 것은 과도하게 예측한다.
이럴 경우 해결책은 일반적으로 x를 변환하는 것이다.

• 만족도 동인 데이터에 대해 유사한 적합화 도면을 생성할 수 있다.
  
  
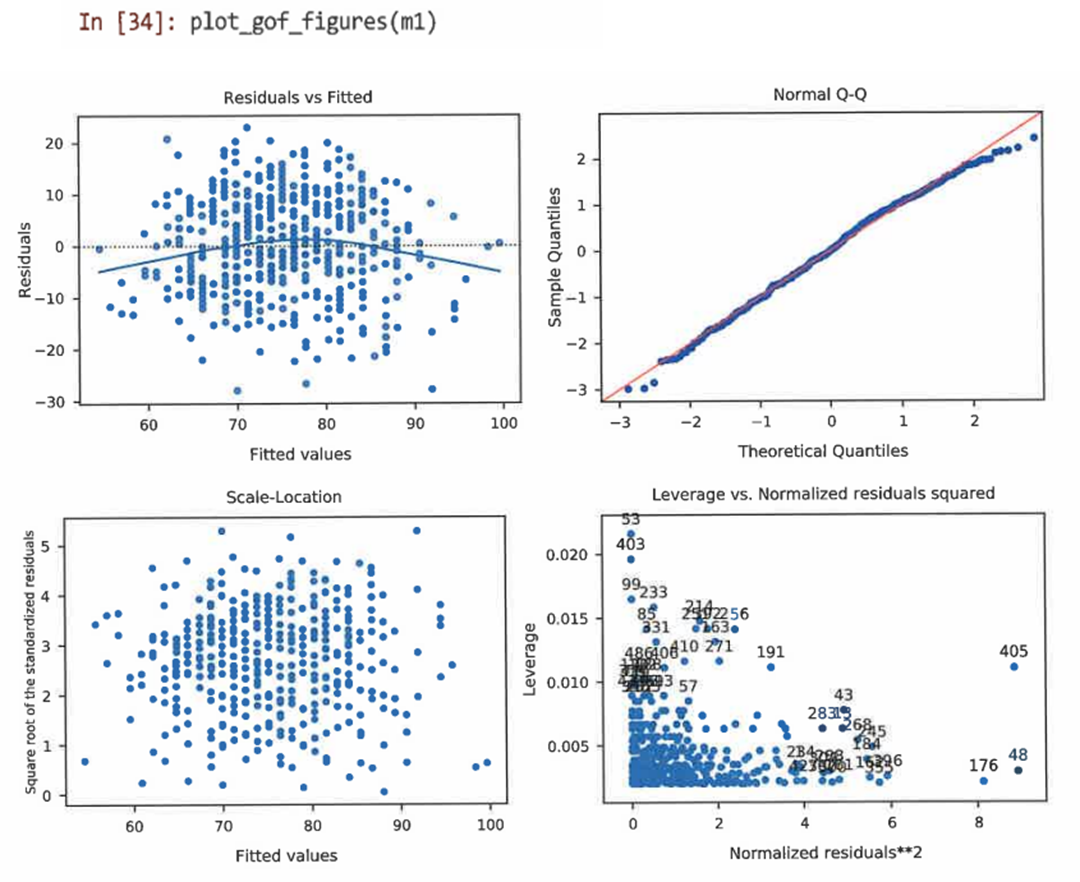
  => 왼쪽 상단 모서리 그림은 적합치 대 잔차를 보여준다. 적합치와 잔차 사이에 명확한 패턴이 없는 것으로 나타나는 것을 보아 잔차가 무작위 오차에 기인한 것이라는 생각과 일치하며, 모델이 합리적이고 명백한 비선형성을 무시하지 않는다는 개념을 뒷받침한다.
  => 왼쪽 아래에 두 번째 그림은 원시 잔차 값을 그리는 대신 잔차 절댓값의 제곱근을 그린다는 점을 제외하고는 첫 번째 그림과 유사하다.

• 잔차 그림의 일반적인 패턴은 원뿔이나 깔때기이다. 분산성, 즉 적합치가 클수록 점차 커지는 오차 범위는 선에 대한 적합화를 최적화하는 선형 모델 가정을 위반한다.

=> 오른쪽 상단 그림은 정규 QQ 도면이다. 잔차가 정규 분포를 따르는지 여부를 확인하는데 도움을 준다. 모델이 적절할 떄 이러한 점들은 유사하고 대각에 가깝다.
=> 오른쪽 하단 패널 그림은 잠재적 특이치, 즉 다른 분포에서 나올 수 있는 관측치를 식별하는데 도움을 준다. 포인트가 고표준화된 잔차 거리와 모델 레버리지를 기반으로 잠재적으로 문제가 되는 특이치인 경우 자동으로 행 번호로 레이블이 지정된다.

• 특이치를 검사하고 데이터에 문제가 있는지 확인하는 것이 바람직하다.
  
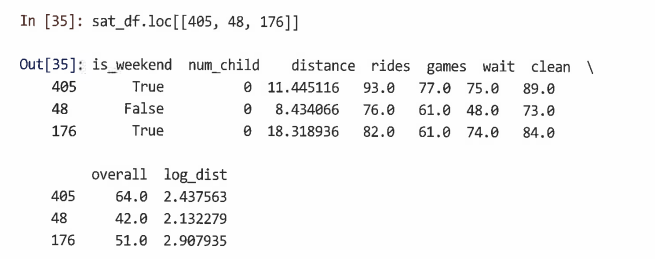
  => 이 경우 값이 1보다 작거나 100보다 큰 경우가 없기 때문에 어떤 데이터 포인트도 명백히 무효인 것이 아닌 것으로 판단하여 특이치를 생략하지 않는다.

7.3 다중 예측자가 있는 선형 모델 적합화

• 다중 변수 모델을 추정하기 위해 모델을 설명하는 공식을 사용해 ols()를 호출한다.
  
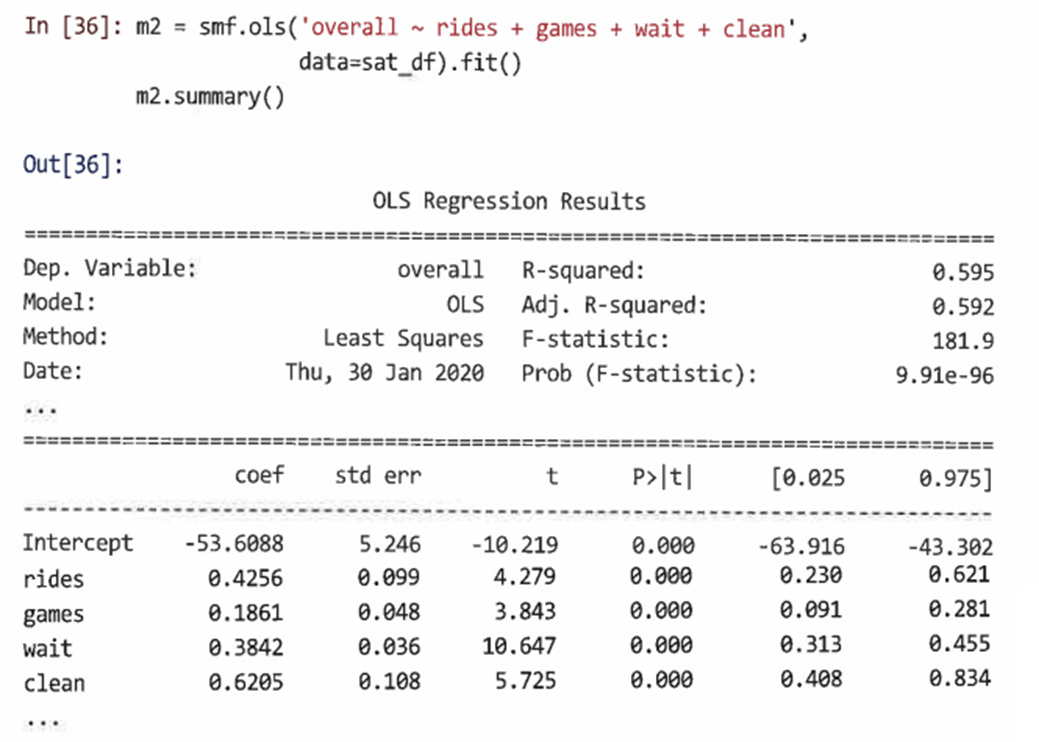
  => 모델은 모든 만족도 항목을 포함해 예측이 향상됐음을 알 수 있다.

• 잔차의 대칭여부를 히스토그램을 그려 확인하고, 모델 계수를 조사한다.

• 각 계수는 다른 예측 변수 값을 조건으로 해당 특징에 대한 만족도와 전체 만족도 간의 관계 강도를 나타낸다.
  => 네 가지 특징 모두 p값, P>|t| <0.05를 통해 통계적으로 유의한 것으로 식별된다.

-도면을 생성해 계수를 시각화하는 것이 더 도움이 된다.

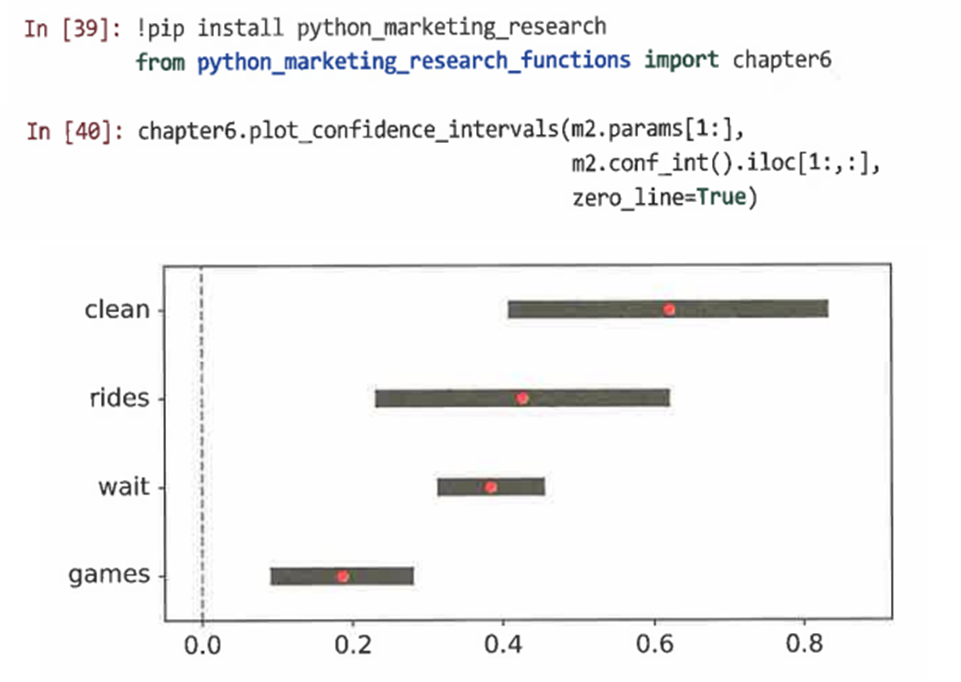
=> 청결에 대한 만족도가 전반적인 만족도와 관련된 가장 중요한 특징으로 추정된다.

7.3.1 모델 비교

• R-제곱 값을 비교해 두 모델을 평가할 수 있다.
  
  => m2가 m1보다 만족도의 변동을 더 많이 설명한다고 말할 수 있다.

• 그러나 예측 변수가 더 많은 모델은 일반적으로 R-제곱값이 더 높으므로 대신 모델의 예측 변수 수를 제어하는 수정 R-제곱 값을 비교해볼 필요가 있다.
  
  => 여전히 m2가 전체 만족도의 변동을 더 많이 설명한다는 것을 암시한다.

• anova_lm()을 사용해 m2가 m1보다 더 많은 변동을 설명하는지 여부를 알아볼 수 있다.
  
  => p값이 낮으면 m2의 추가 예측 변수가 모형의 적합도를 크게 향상시킨다는 것을 나타낸다. 따라서 m2이 더 정확한 모델이라고 볼 수 있다.

7.3.2 모델을 사용해 예측하기

• 모델 계수를 사용해 설명 변수의 다양한 조합에 대한 overall 결과를 예측할 수 있다.

• 4개의 개별 측면을 각각 100점으로 평가한 고객의 전체 평가를 예측하려면 해당 평가에 계수를 곱하고 절편을 추가할 수 있다.
  
  => 최적 추정치는 108.024이며, 이는 최고 점수보다 높다. 모든 것을 100점으로 평가하는 사람은 또한 전체적으로 100점을 줄 가능성이 있음을 알 수 있다.

• ols.predict()를 사용해 더 효율적으로 모델 예측을 계산할 수 있다.
  
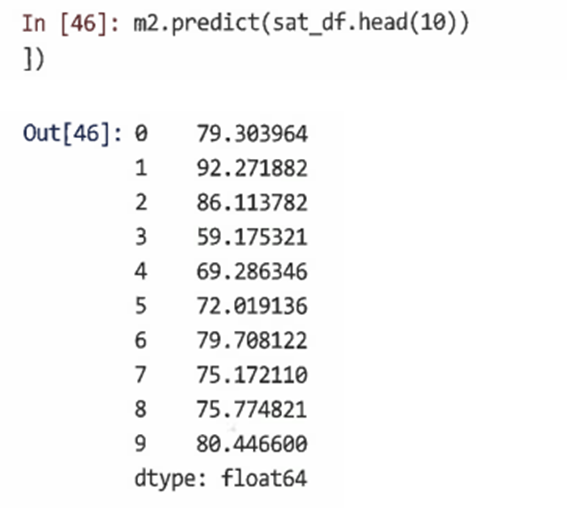
  => 이를 통해 원하는 범위에 대한 예측을 얻을 수 있다. 이 경우 처음 10명의 고객에 대한 예측을 얻을 수 있다.

7.3.3 예측자 표준화

• 계수를 비교하려는 경우 모델을 적합화하기 전에 공통 척도로 데이터를 표준화하면 좋다.

• 가장 일반적인 표준화는 값을 0을 중심으로 표준 편차 단위로 변환하는 것이다. 이는 각 관측치에서 변수의 평균을 뺀 다음 표준 편차(std())로 나누며 Z 점수라고도 한다.
  

• 변수의 크기에 대해 걱정하지 않고 상대적인 기여도만 고려한다면, 크기가 조정된 버전의 sat_df를 만들 수 있다.
  

• 표준화 후에는 결과를 확인해야 한다. 표준화된 변수는 평균이 0이고 값은 평균으로부터 몇 단위 이내에 있어야 한다. describe()로 확인해볼 수 있다.
  
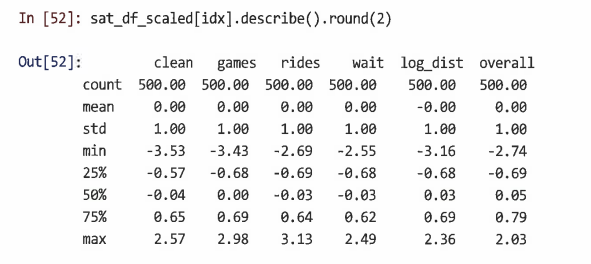
  => 단, 이 때 절편이 0이 되어도 제거하면 안된다. 절편은 표준화 후에도 모델에 계속 남아있어야 한다.

7.4 요인을 예측자로 사용

• 모델을 개선하기 위해 주말에 오거나 먼 곳을 여행하는 고객, 혹은 다자녀의 경우 만족도가 서로 다른지 다음 예측 변수를 모델에 추가해 확인해본다.
  
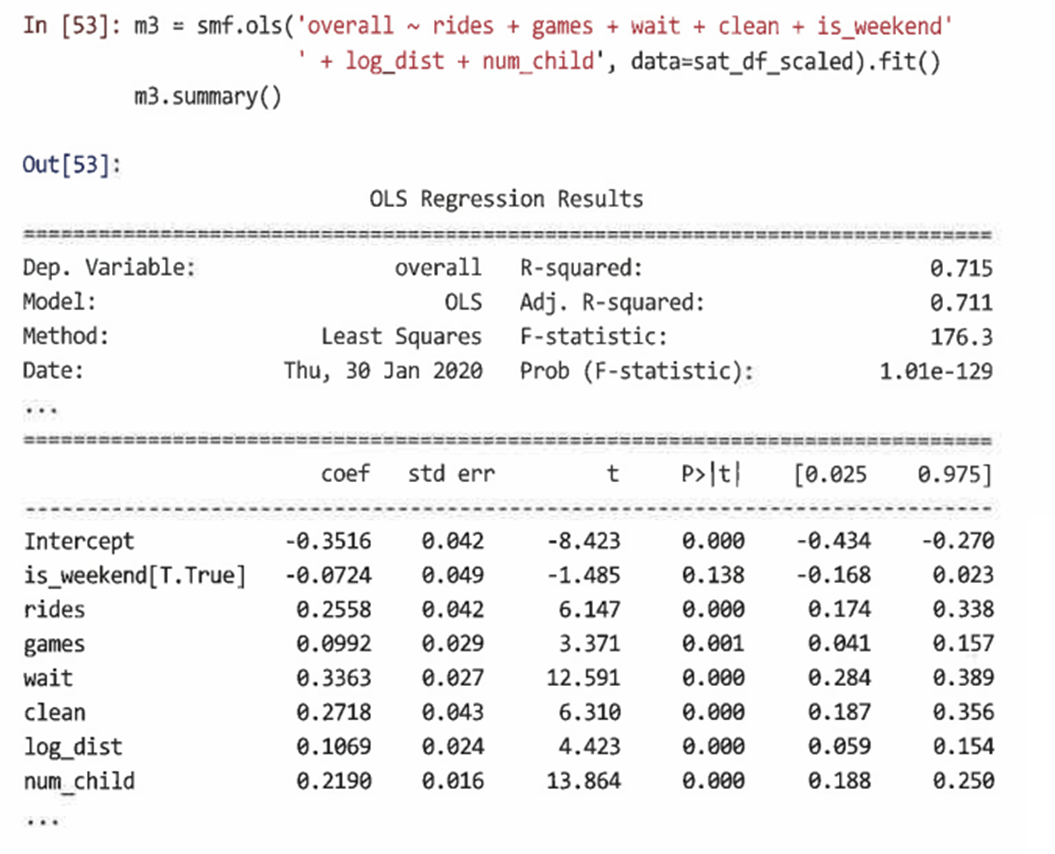
  => 모델 요약은 적합도(R-제곱)가 크게 향상되었으며, log_dist와 num_child에 대한 계수가 0보다 상당히 큰 것을 보아 더 멀리 여행하고 더 많은 자녀를 둔 사람들이 전반적인 만족도 등급이 더 높다는 것을 알 수 있다.

• 데이터에 요인이 포함된 경우 데이터 유형에 주의해야 한다.

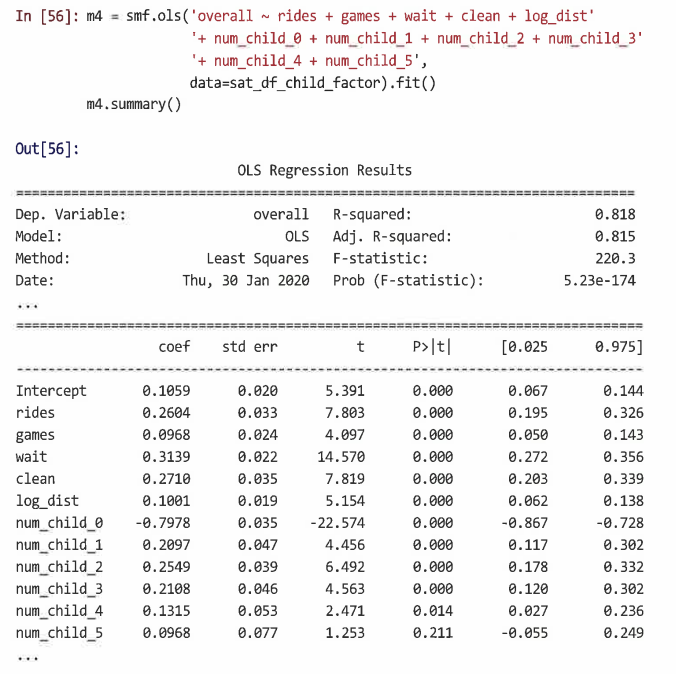
• 이 경우 num_child는 0-5 범위의 숫자 변수이지만, 이를 숫자로 취급하는 것이 반드시 의미가 있지는 않다. 따라서 요인으로 변환하고 모델을 재추정한다.
  
  

• pandas.get_dummies()를 사용해 num_child가 1명을 나타낼 때 1, 그렇지 않으면 0을 나타내는 변수 num_child_1을 생성하고, 마찬가지로 6까지 생성한다.

=> 이제 num_child에 대해 6개의 적합 계수가 있음을 알 수 있다. 그룹에 있는 어린이 수에 관계없이 전반적인 만족도의 증가가 거의 동일하다는 것이 확인된다. 즉, 실제로 각 어린이 수의 증가를 다르게 추정할 필요가 없음을 시사한다.

• 대신 그룹에 자식이 있으면 TRUE, 없으면 FALSE인 has_child라는 새 변수를 선언해 모델을 추정한다.
  

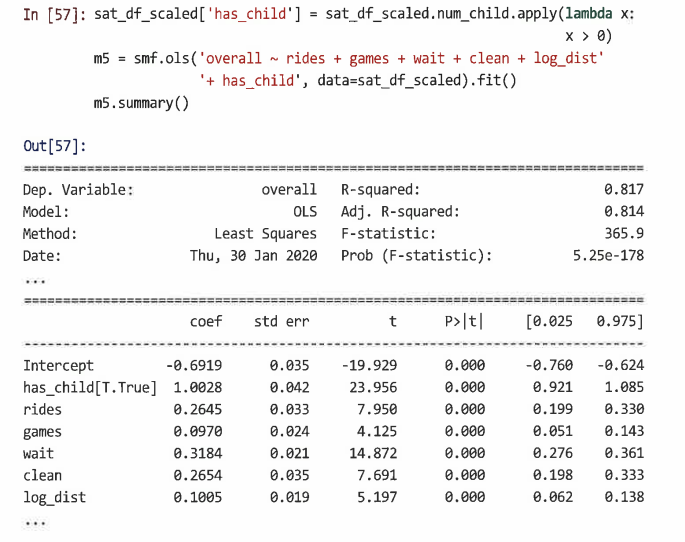
7.5 상호 작용 항

• 수식의 변수 간에 : 연산자를 사용해 두 용어의 상호 작용을 포함할 수 있다.

• 만족도 등급과 방문을 설명하는 두 가지 변수 no_child와 is_weekend 간의 상호 작용을 사용해 새 모델을 만든다.
  
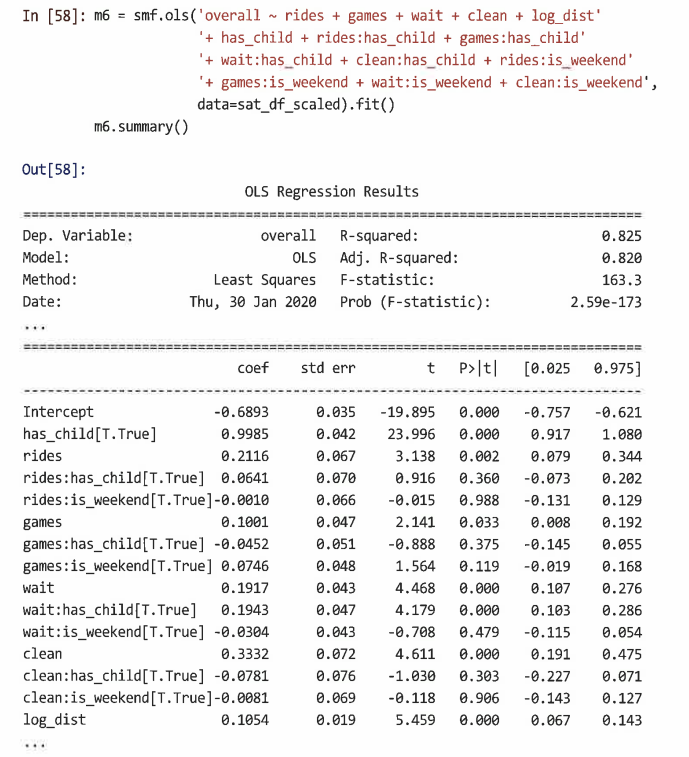
  => 공원과 has_child 및 weekend의 특징에 대한 등급 사이에 8개의 상호 작용 항이 포함된다. 이러한 상호 작용 중 하나(wait:has_child)만 중요하기 때문에 중요하지 않은 상호 작용은 삭제할 수 있다.
  
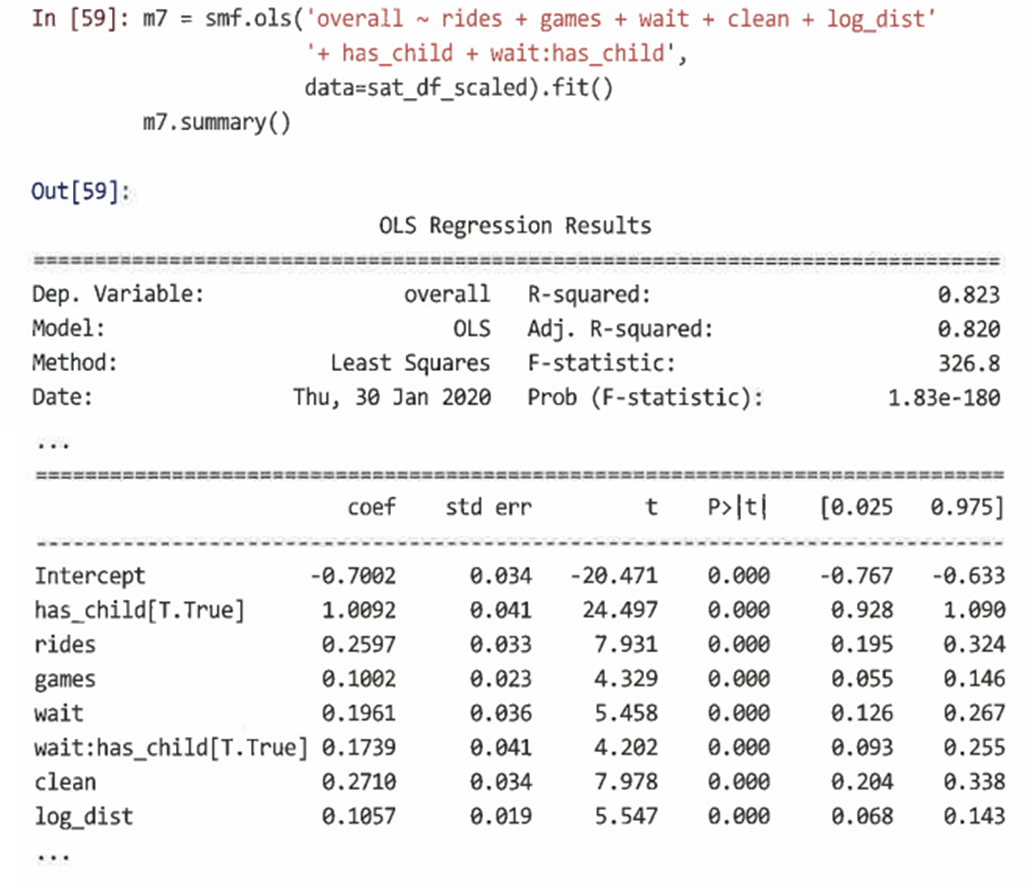
  => 이 결과를 통해 아이들과 함께 공원에 간 그룹으로부터 더 높은 만족도를 예측할 수 있으며, 아이들이 없는 사람들보다 아이들이 있는 사람에서 대기 시간이 더 중요한 예측 변수임을 알 수 있다.

• 모델에 상호 작용 항을 포함할 때 두 가지 중요한 점:

1. 계수에 대해 해석 가능하고 비교 가능한 척도를 갖기 위해 상호 작용을 모델링할 때 예측 변수의 표준화를 고려하는 것이 특히 중요하다.
2. 상호 작용 효과를 포함할 때 항상 주 효과(x+y)를 포함해야 한다.

7.5.1 언어 요약: 고급 수식 구문

7.5.2 주의! 과적합

• 모형에 예측 변수를 추가하면 효과 수와 변수 간의 연관성으로 인해 계수 추정치의 정확도가 떨어진다. ols() 출력에서 더 큰 계수 표준 오차로 나타나고 곧 추정치의 신회도가 낮음을 의미.
• 추정치에 대한 잠재적으로 낮은 신뢰도에도 불구하고 모델에 변수를 추가하면 R-제곱값이 점점 더 높아진다. 언뜻보면 모델이 점점 더 좋아지는 것처럼 보이지만, 계수 추정치가 정확하지 않으면 모델의 유용성이 떨어진다.

=> 과적합(overfitting): 너무 많은 변수를 추가하고 덜 정확하거나 부적절한 모델로 끝나는 과정

• 이를 피하기 위해서:

1. 계수의 표준 오차를 면밀히 주시해야 한다. 작은 표준 오차는 모형을 추정하기에 충분한 데이터가 있음을 나타내는 지표이다.
2. 보유할 데이터의 하위 집합을 선택하고 모델을 추정하는데 사용하지 않는다. 홀드아웃 데이터에 predict()를 사용해 얼마나 잘 수행되는지 확인한다.

7.5.3 선형 모델 적합화를 위한 권장 절차

7.6 요점