세그멘테이션: 부분 모집단 탐색을 위한 비지도 클러스터링 방법

10.1 세그멘테이션 철학

시장 세그멘테이션의 목표: 관심 제품, 시장 참여, 마케팅 노력에 대한 반응과 관련된 주된 방식이 서로 다른 고객 그룹을 찾는 것.

10.1.1 세그멘테이션의 어려움

• 세그멘테이션에서 중요한 것은 그 결과가 특정 비즈니스 요구에 '의미 있는 결과를 보장하는가' 이다.
• 이러한 모델을 찾을 수 있는 가능성을 최대화하기 위해서 분석가는 2가지를 예측할 필요가 있다.
  첫째, 세그멘테이션 프로젝트는 '세그멘테이션 연구 실행'이나 '데이터에 대한 세그멘테이션 분석 수행'의 문제가 아니다.
  둘째, 여러 차례 시행착오를 겪으며 먼저 수집해야 할 중요한 데이터가 무엇인지 결정하고, 그 다음에는 솔루션을 개선 및 테스트하고, 비즈니스 이해관계자와 함께 해석을 수행해 가능한 결과를 찾아야 한다.

10.1.2 클러스터링으로서의 세그멘테이션과 분류

• 지도 학습의 모델은 새로운 관찰 독립 변수로부터 결과 상태를 예측하려는 목표와 함께 결과 상태(종속 변수)가 알려진 관측치와 함께 제공된다.
• 비지도 학습의 모델은 결과 그룹에 대해 알지 못하지만 데이터 구조에서 이를 발견하려고 한다.
• 클러스터링은 비지도 학습에 해당한다.

10.2 세그멘테이션 데이터

• 책 웹사이트에서 데이터셋을 다운로드한다.
  

• 데이터를 확인한다.
  

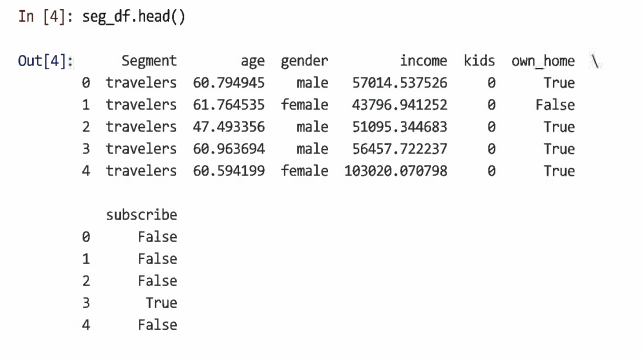
10.3 클러스터링

거리 기반 클러스터링: 그룹 내 구성원 간의 거리를 최소화하는 동시에 다른 그룹과의 거리를 최소화하는 그룹을 찾으려고 시도한다.

• 계층적 클러스터: 데이터를 트리 구조로 모델링해 이를 수행
• k-평균: 그룹 중심(중심점)을 사용

모델 기반 클러스터링: 데이터를 서로 다른 분포에서 샘플링한 그룹의 혼합으로 보지만 원시 분포와 소속 그룹에 대한 정보는 '손실'된 것이다.

• 가우스 혼합 모델: 관측된 분산이 다른 평균과 표준 편차 같은 특정 분포 특성을 가진 소수의 가우스 변수로 가장 잘 표현될 수 있도록 데이터를 모델링

10.3.1 클러스터링 단계
클러스터링 분석에는 크게 두 단계가 필요하며, 각 기법은 다음 절차를 거친다.

1단계. 데이터 변환 및 크기 조정

• 데이터셋의 모든 범주형 변수가 이진으로 되어있기 때문에, 숫자형으로 바꾸어 준다.
  
• 데이터 크기를 조정해준다.
  

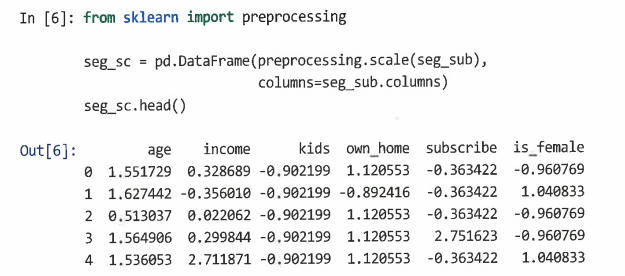
2단계. 간단 검사 함수

• 세그먼트 검사: 클러스터링으로 제안된 솔루션이 비즈니스 문제에 유용한지 확인하기 위해 데이터를 요약하고 그룹 간의 높은 수준의 차이를 빠르게 검사할 수 있는 간단한 함수를 작성하는 것.
• pandas의 pivot_table() 함수를 사용한다.
  
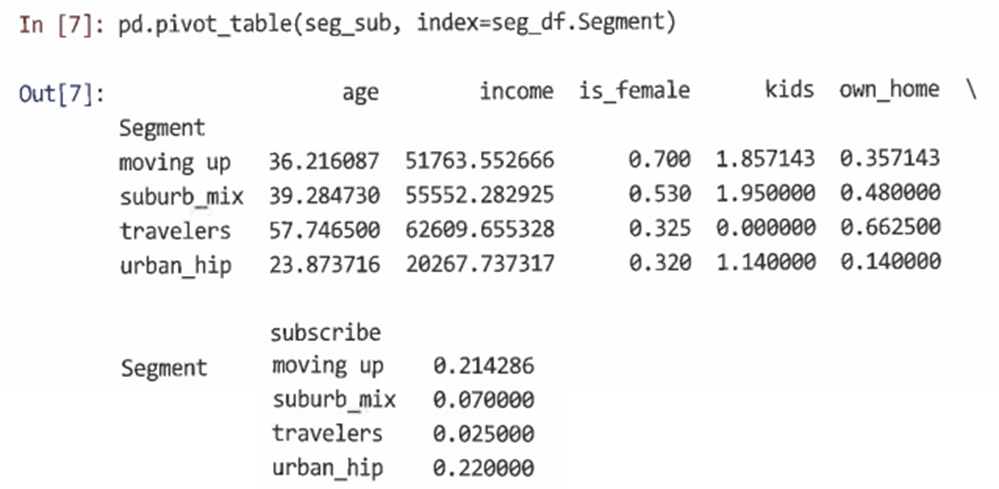
• aggfunc 인수를 사용해 모든 적절한 함수나 함수 리스트를 전달할 수 있다.
  
  => 이러한 종류의 요약 함수를 통해 다음과 같은 비즈니스 가치와 관련된 질문에 쉽게 답변할 수 있다.
• 그룹 평균에 명백한 차이가 있는가?
• 차별화 부분이 몇 가지 근본적인 스토리를 만드는가?
• 단일 데이터 수준의 값과 같은 평균과 같이 이상한 결과가 바로 표시되는가?

10.3.2 계층적 클러스터링
쌍별 거리: 계층적 클러스터화의 주 정보는 관측치 간의 거리이다.

• 2개의 관측치 X와 Y의 경우 유클리드 거리 d
  

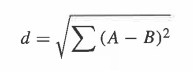
• 단일 관측치 쌍일 경우
  

• 여러 쌍일 경우 Scipy distance 모듈의 pdist()함수를 사용
  

• 그러나 유클리드 거리는 관측값이 숫자일 때만 정의된다는 단점이 있다. 따라서 경우에 따라 데이터셋을 숫자형으로 부울 열로 변환해야 한다.

• scipy.spatial.distance 모듈의 squareform 함수를 사용해 거리 행렬을 계산할 수도 있다.
  
  => 이를 통해 1, 2, 3번째 행의 각 거리를 알 수 있다.

• 좀 더 간결한 형식을 얻기 위해 압축된 벡터 형식의 거리 행렬을 반환하는 pdist()를 사용한다.
  

• 적절히 데이터의 크기를 조절해야 데이터의 행에 의해 지배된 고도로 치우친 거리 분포를 피할 수 있다.
  

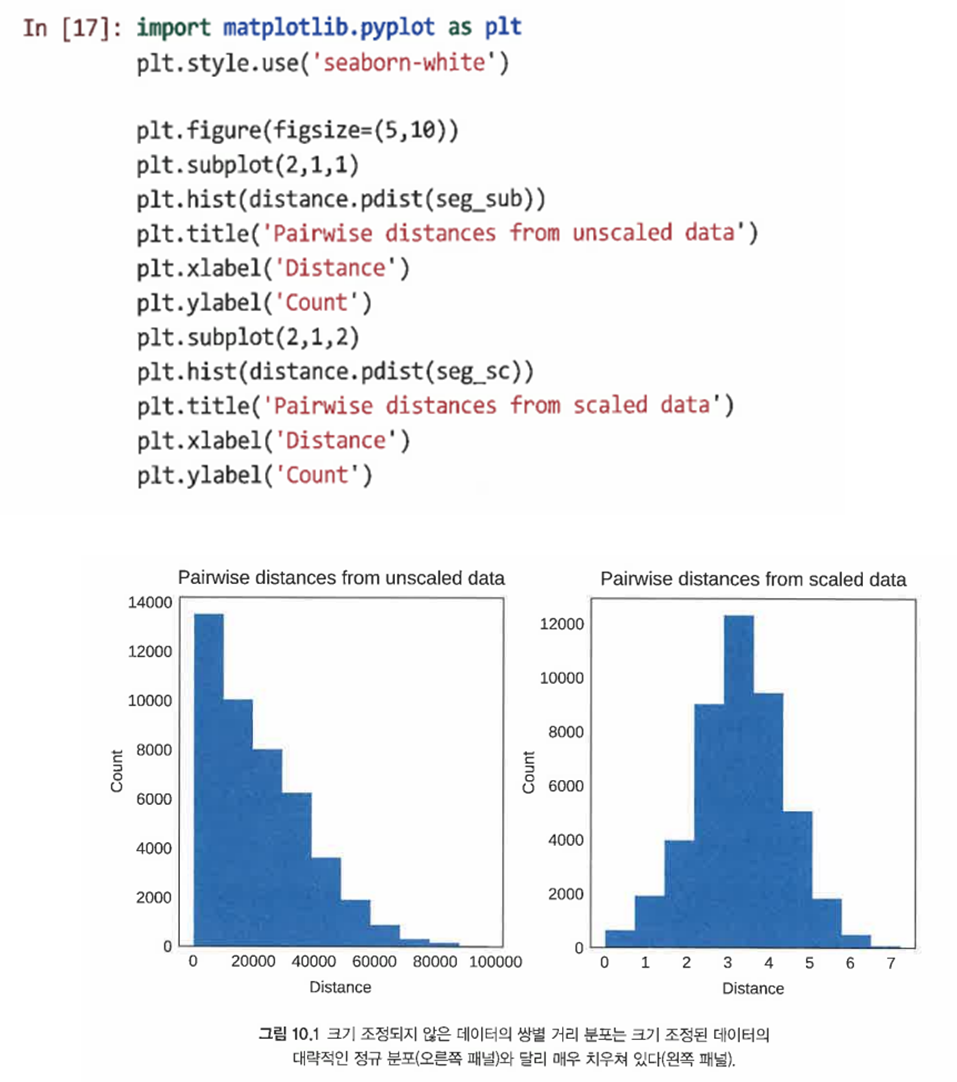
파이썬에서의 계층적 클러스터링: Scipy hierarchy 모듈의 linkage() 함수를 사용해 계층적 클러스터링을 생성한다.

=> 전체 클러스터 내 분산을 최소화하는 그룹을 형성하는 ward 연결 방법 사용

• 연결 행렬을 dendrogram() 함수에 전달하면 연결 행렬을 나타내는 트리가 도식화된다.
  
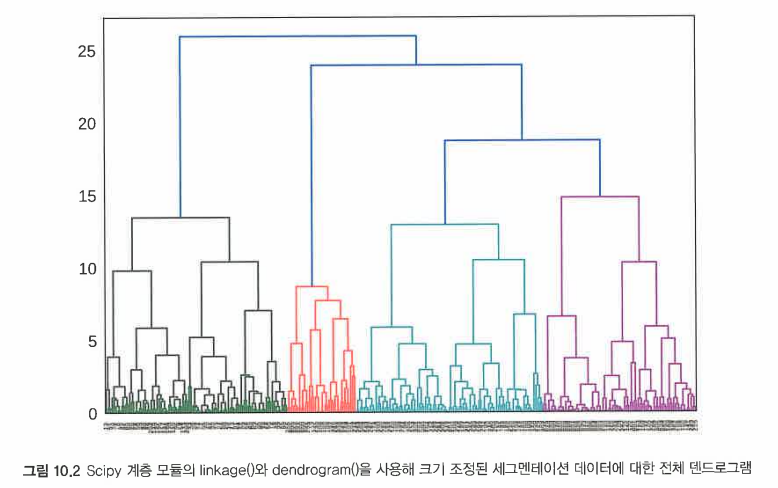
  => 그러나 이는 읽기 어렵기 때문에 다음과 같은 두 방법을 사용해 가독성을 높일 수 있다.

1. dendrogram()에서 truncate_mode()와 p인수를 사용하는 것.
   p는 잘림의 정도를 의미하여, lastp 모드에서는 p개의 가지만 표시된다.
   

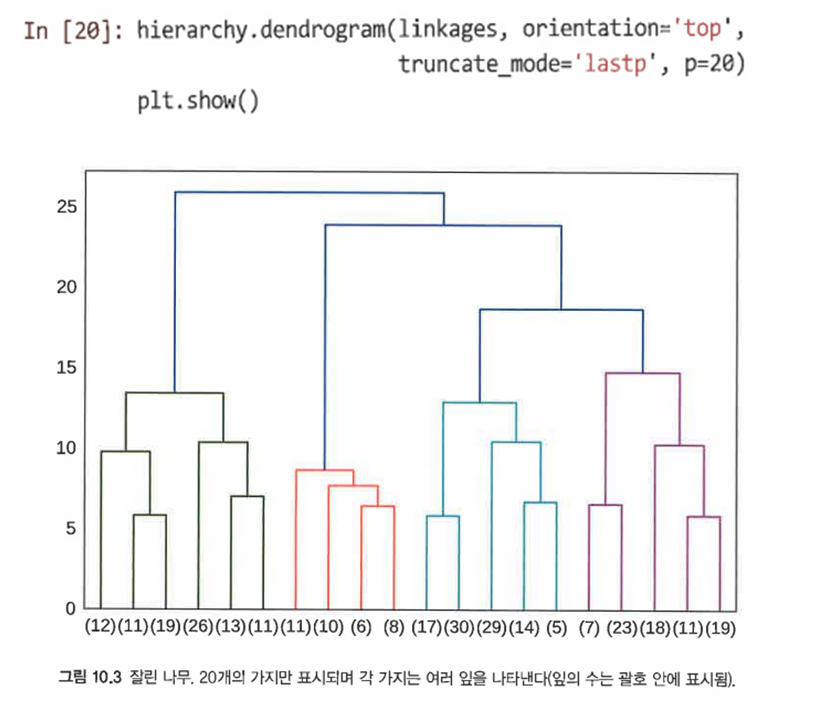
2. xlim()함수를 사용해 차트의 한 단면을 확대해보는 것.
   

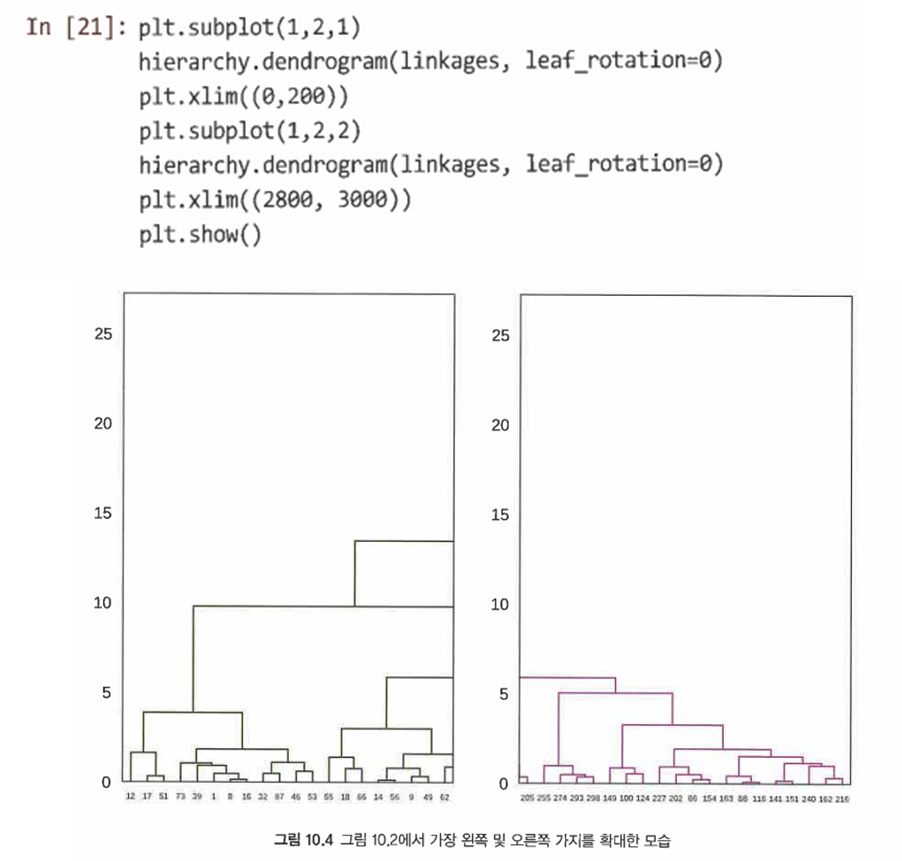
• 계층적 클러스터 솔루션에 대한 적합도 척도를 사용해 계층 트리가 고객 사이의 거리를 잘 나타내고 있는지 확인해 볼 수 있다.
• 코페네틱 상관 계수 cophenet()를 사용해 연결로부터의 거리를 pdist() 측도와 비교
  
  => CPCC가 0.6으로 적절히 강한 적합화를 의미한다.

10.3.3 계층적 클러스터링 계속: fcluster의 그룹

• 덴드로그램은 원하는 높이에서 클러스터로 절단할 수 있기 때문에 원하는 그룹 수를 지정해야 한다.

• color_thresh 인수를 전달해 덴드로그램이 잘리는 위치를 기준으로 클러스터를 볼 수 있다.
  

• fcluster()를 사용해 관측값에 대한 할당 벡터를 얻는다.
  
  => fcluster()는 각 관측값에 대한 클러스터 레이블을 반환한다. np.unique(return_counts=True)를 사용해 각 클러스터에 대한 관측치 개수를 얻는다.

• sug_sub()의 변수를 다음 4개의 클러스터에 대해 검사한다.
  
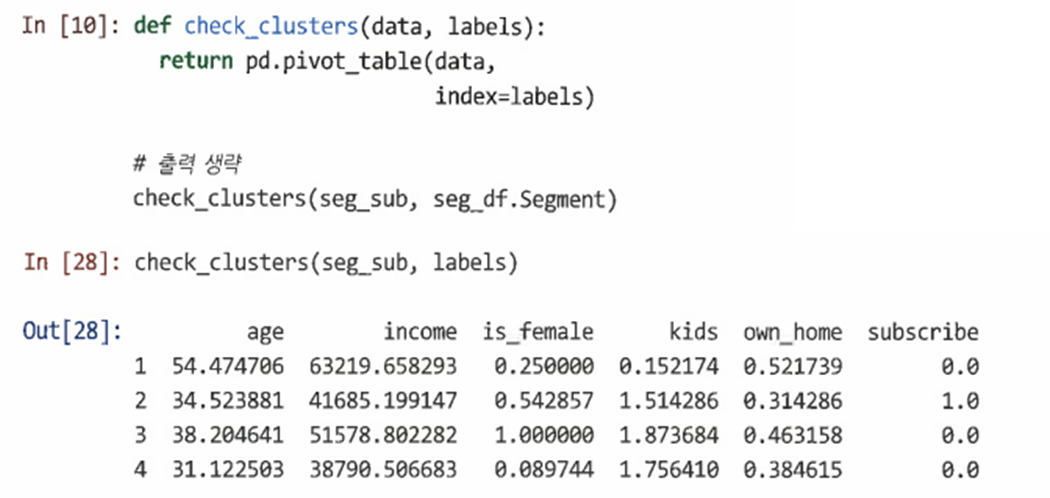
  => 이때, 그룹 2에는 모든 구독자가 포함되어 있음을 알 수 있다.

10.3.4 평균 기반 클러스터링: k_means()
k-평균 클러스터화: 할당된 그룹의 다변량 중심에서 각 관측치의 제곱합의 평균 편차 측면에서 가장 간결한 그룹을 찾으려고 한다.

• 평균 수는 지정해야 하는 매개변수이다.
• 다음과 같은 두 단계를 번갈아가며 수행한다.

1. 할당: 각 관측치는 가장 가까운 평균으로 나타난 클러스터에 할당되며, 근접성은 제곱 유클리드 거리의 최솟값으로 정의된다.
2. 갱신: 공통적으로 새로운 평균이 되는 각 클러스터의 중심을 계산한다.

• 평균 편차를 명시적으로 계산하기 때문에 k-평균 클러스터화는 유클리드 거리에 의존한다. 따라서 계층적 클러스터링과 달리 수치 데이터나 수치로 변환될 수 있는 데이터에만 적합하다.

• scikit-learn의 클러스터 모듈에서 k_means() 함수를 실행할 수 있다.
  
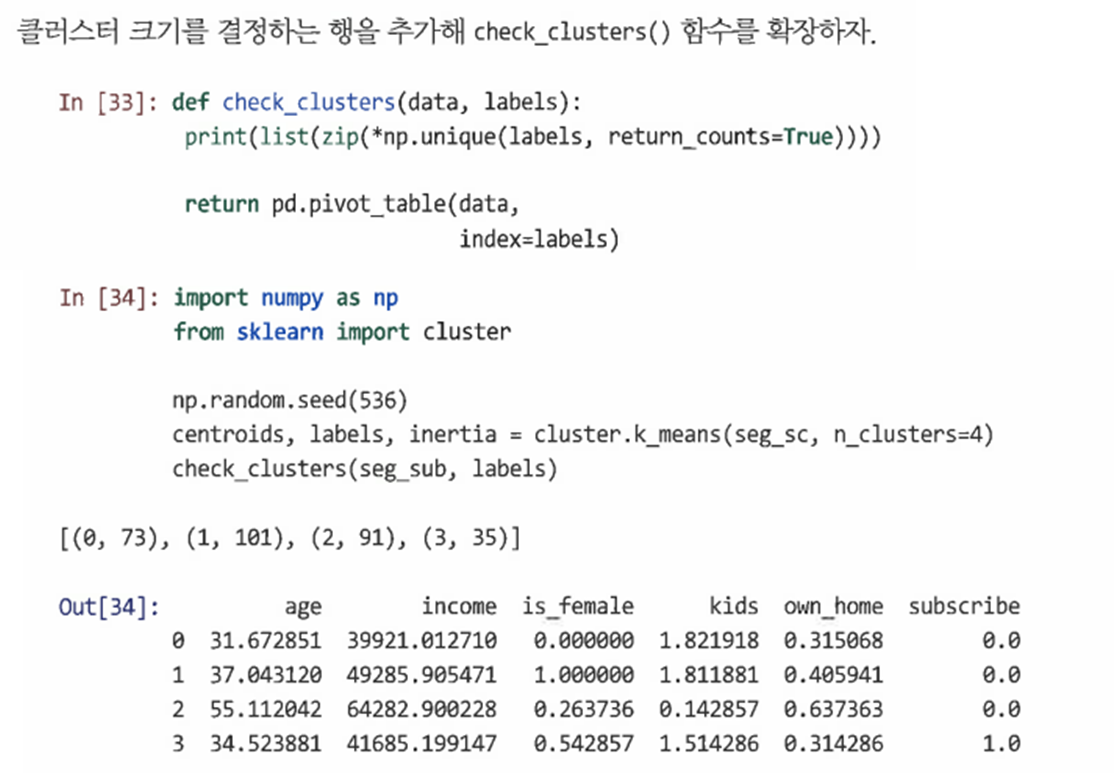
  => 이러한 클러스터는 크기 조정된 데이터의 계층적 클러스터링에서 찾은 클러스터와 표면적으로 매우 유사하며, 모든 구독자가 포함된 그룹이 보인다.
  => 그룹 0과 1은 성별에 의해 나뉜 그룹으로 유용하지 않다.

• 만약 크기를 조정하지 않은 데이터를 사용한다면?
  
  => 3개와 4개의 그룹으로 각각 클러스터를 나누면 다른 흥미로운 인사이트를 도출할 수 있다.

10.3.5 모델 기반 클러스터링: GaussianMixture()

• 모델 기반 클러스터화의 핵심 아이디어는 통계적 분포가 다른 그룹에서 관측치를 가져온다는 것이다. 즉, 혼합 모델이라고도 한다.
• 각 모델은 임의 매개변수로 시작해 다음 단계를 반복한다.

1. 할당: 각 관측치가 속할 가능성이 가장 높은 성분에 할당된다.
2. 갱신: 할당된 포인트가 주어지면 각 성분에 대한 매개변수가 갱신된다.

• GaussianMixture()는 정규 분포로 데이터를 모델링하기 때문에 숫자 데이터만 사용한다.

• 모델은 GaussianMixture()의 fit() 메서드를 사용해 추정되고 레이블은 predict() 메서드를 사용해 생성된다.
  

• GaussianMixture()는 모델 구성 요소의 수와 각 구성 요소 내의 공분산 구조를 입력으로 취한다.

• 베이즈 정보 기준(BIC)를 통해 모델 적합도를 측정할 수 있다.

• 먼저, 다른 성분 개수의 모델을 적합화하며 BIC값을 비교해 최적의 클러스터 수를 결정한다.
  
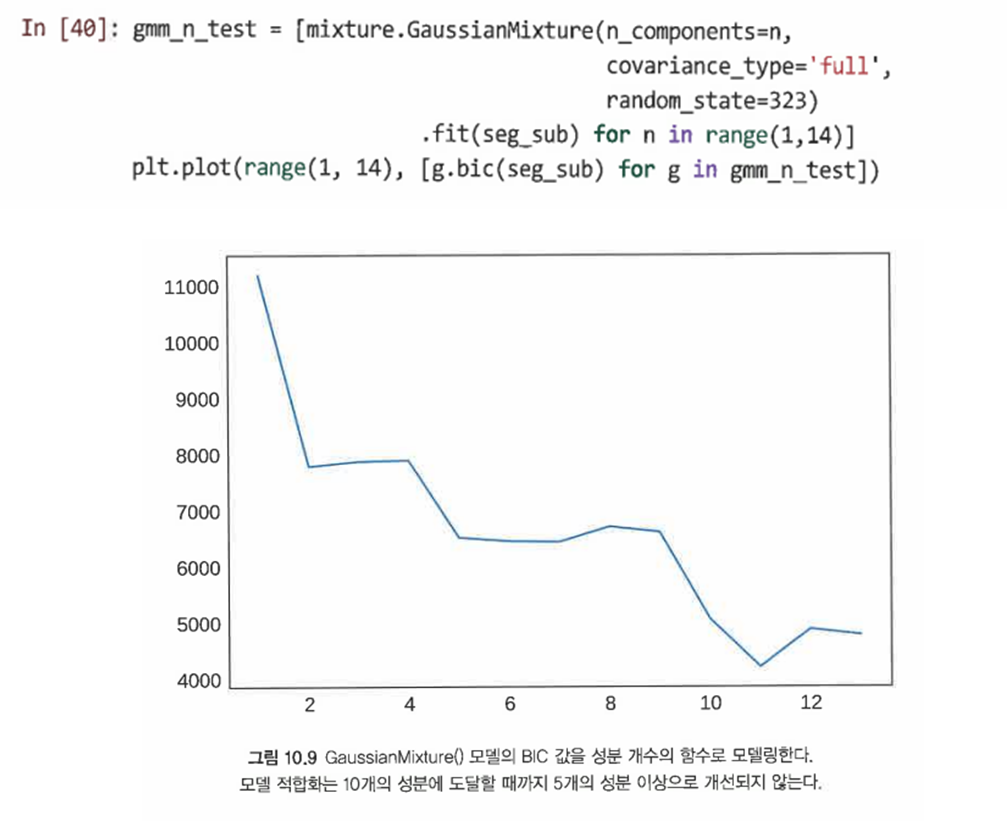
  => BIC 값이 낮을수록 더 나은 모델 적합도를 의미한다.

• 공분산 유형과 성분 개수를 변경함으로써 모델을 더 개선할 수 있다.
  
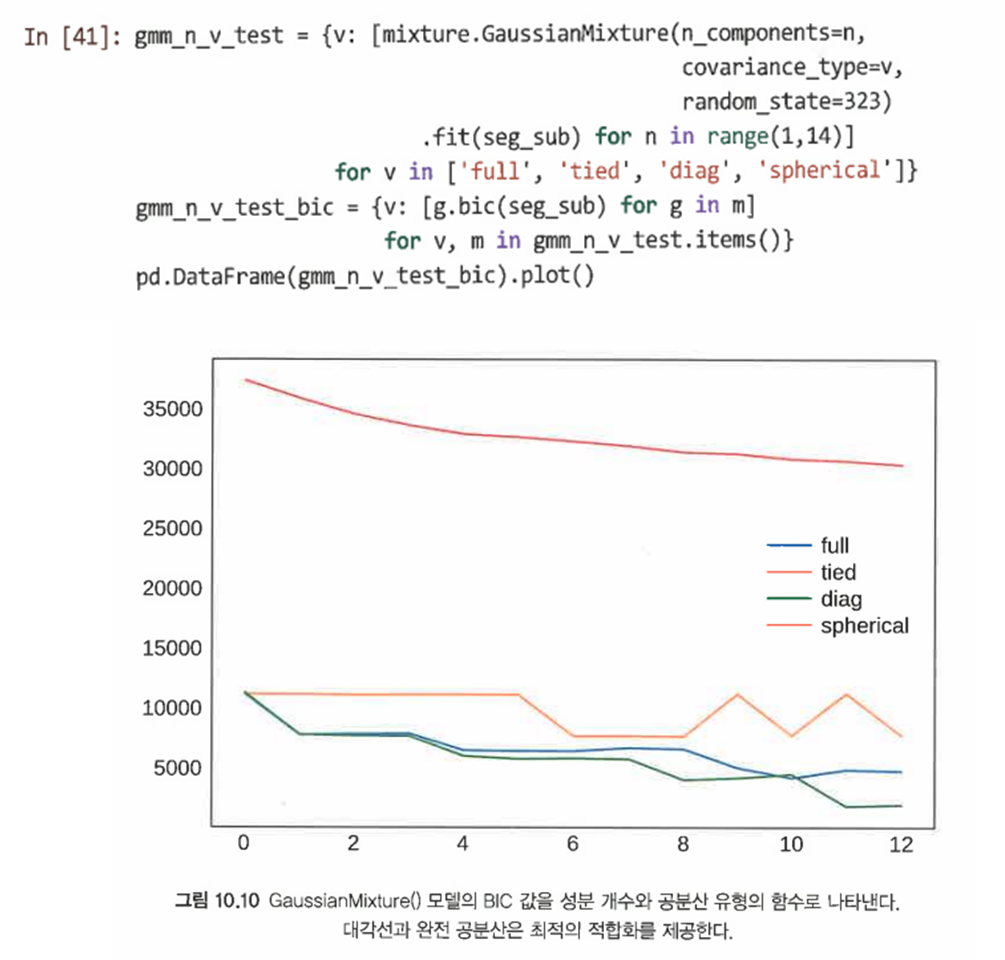
  => 대각 공분산이 최적의 적합화를 보여주고 6개의 성분 개수를 적절해 보인다.

• 6개의 성분 개수로 찾은 클러스터를 살펴본다.
  
  => 그러나 이러한 클러스터는 실행 가능해 보이지 않는다.

10.3.6 클러스터링 요약

• 다른 기법은 다른 솔루션을 산출할 가능성이 높으며 일반적으로 절대적인 '정답'이란 없다. 잠재적 클러스터 수를 달리하는 여러 클러스터링 방법을 시도해보길 권한다.
• 세그멘테이션의 결과는 주로 비즈니스 가치에 관한 것이며, 솔루션은 모델 적합성과 비즈니스 유용성 측면에서 평가돼야 한다. 모델 적합성은 중요한 기준이며 간과해서는 안 되지만, 궁극적으로 이해관계자가 답변을 전달하고 사용할 수 있어야 한다.

10.4 요점