분류: 알려진 범주에 관측치 할당

11.1 분류

• 클러스터링은 그룹 멤버십을 발견하는 프로세스인 반면, 분류는 멤버십의 예측
• 분류는 상태가 알려진 관측치를 사용해 예측 변수를 도출한 다음 해당 예측 변수를 새 관측치에 적용한다.
• 분류 프로젝트에는 일반적으로 최소한 다음 단계가 포함된다.
  

11.1.1 나이브 베이즈 분류: GaussianNB()

• 나이브 베이즈는 훈련 데이터를 사용해 독립이라고 간주되는 각 예측변수 함수로서 부류 구성원의 확률을 학습한다.

• 새로운 데이터에 적용할 때 부류 멤버십은 예측자의 조합에 의해 할당된 결합 확률에 따라 가능성이 높은 범주로 할당된다.

• scikit-learn의 naive_bayes 라이브러리를 사용한다.
  
  => 데이터를 훈련 데이터와 테스트 데이터로 분류한다. 이때 훈련에 사용할 데이터의 70%를 선택하고 선택하지 않은 부분을 홀드아웃 데이터로 유지한다.

• 훈련 데이터를 사용해 나이브 베이즈 분류기를 훈련시켜 훈련 집합의 다른 모든 변수로부터 세그먼트 멤버십을 예측한다.
  
  => nb.class_prior의 값을 통해 모델 작동 방식에 대한 통찰을 얻을 수 있다.

• 훈련 데이터와 데이터 모두에 대해 예측을 생성할 수 있으며 일부 사용자에 대한 참 값과 예측 레이블을 확인해 볼 수 있다.
  
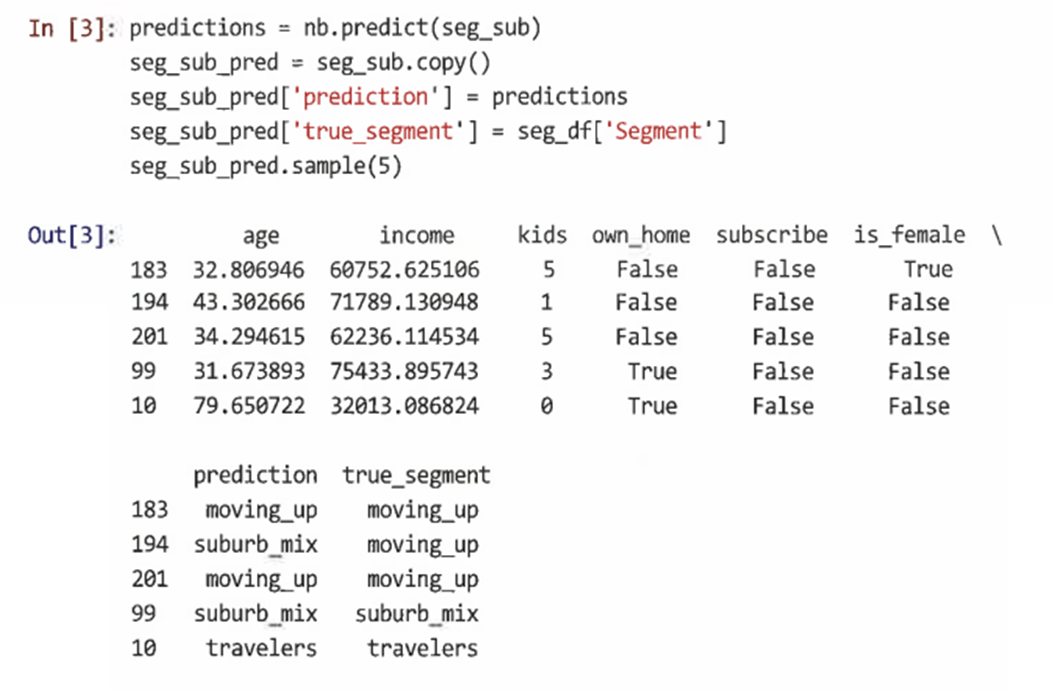
  => predict 열과 true_segment 열을 비교하면 모델이 잘 수행되고 있는 것으로 보인다.

• 테스트 데이터에 score() 메서드를 사용해 모델의 정확성을 확인할 수 있다.
  
  => 이를 통해 예측된 세그먼트 멤버십과 참 세그먼트 멤버십 간에 일치된 값인 정확도 점수를 알 수 있다. 이 경우 약 85%이다.

• average() 매개변수는 4개의 다른 세그먼트의 성능을 결합하는 방법을 지정한다. 혼동 행렬(confusion matrix)을 사용해 각 범주의 성능을 비교할 수 있다.
  
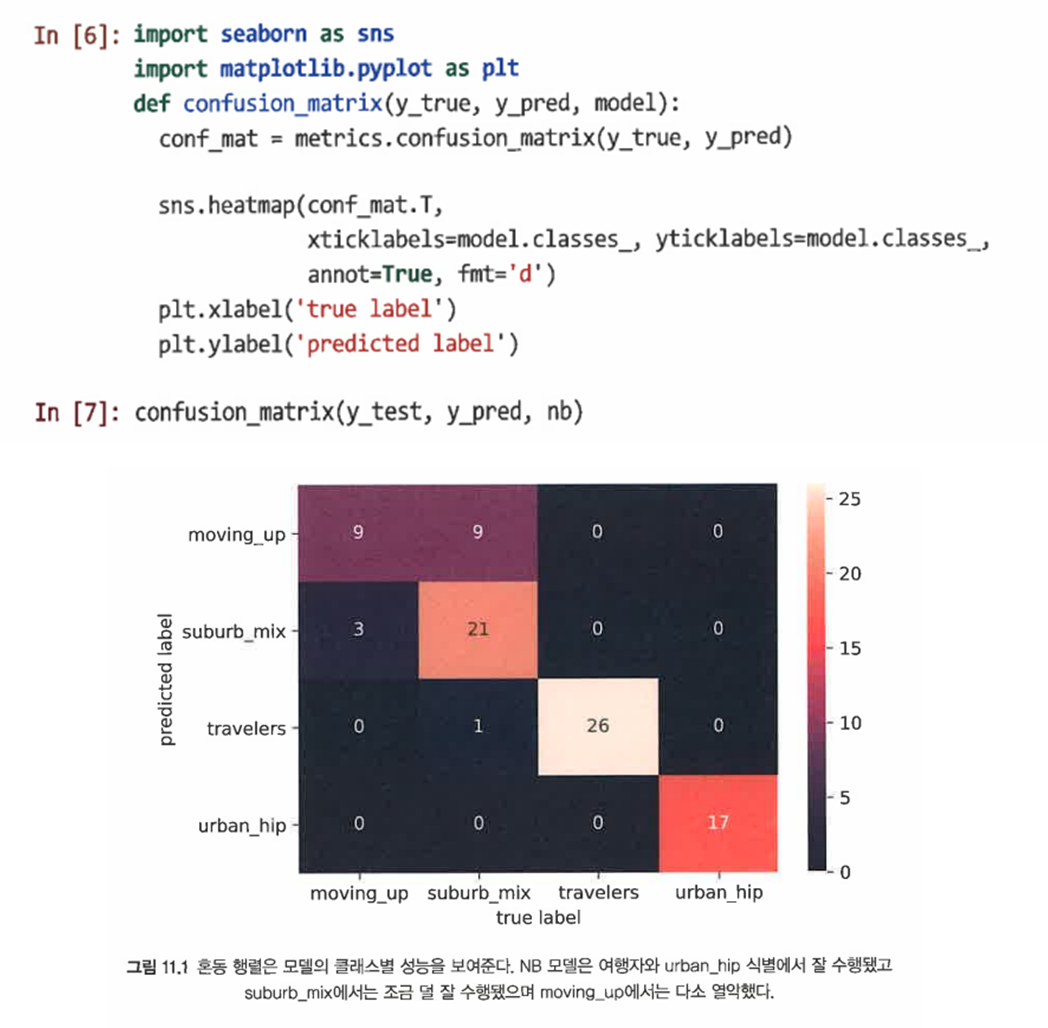
  => NB 예측은 moving_up을 제외하고 각 세그먼트에서 대부분의 관측치에 정확했음을 볼 수 있다.
  => 그러나 완전 정확하게 분류해내지는 못했다. 이는 예측의 비대칭성을 보여준다.

• 모델은 참 긍정과 참 부정을 모두 정확하게 식별해야 한다. 머신러닝의 두 가지 중요한 통계 개념에 해당하는 이러한 요구 사항 사이에는 상호 보완성이 있다.

첫 번째. 정밀도: 모든 긍정 중 참 긍정인 레이블의 비율

두 번째. 민감도: 모든 긍정 비율 중 제대로 식별된 비중

• F1 점수를 알아보기 위해서는 정밀도와 민감도를 사용한다.
  

• F1을 파이썬 함수로 나타내면 다음과 같다.
  

• 10장에서 작성한 요약 함수를 사용해 예측된 세그먼트의 요약 값을 확인한다.
  
  => 제안된 세그먼트에 대한 인구 통계 요약은 참 세그먼트의 값과 매우 유사함을 알 수 있다.

• 나이브 베이즈 모델의 경우 가장 가능성이 높은 세그먼트뿐만 아니라 predict_proba() 메서드를 사용해 각 세그먼트의 멤버십 승산비도 추정할 수 있다.
  
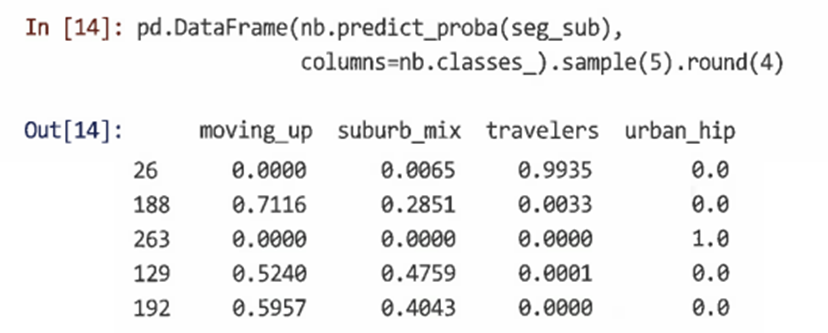
  => 응답자 188이 Moving up일 가능성이 약 71%이고 Suburban mix에 있을 가능성이 29%라는 것을 알려준다. 이처럼 개인 수준 세부 정보는 어떤 개인을 타기팅할지 제안할 수 있다.

11.1.2 랜덤 포레스트 분류: RandomForestClassifier()

• 랜덤 포레스트 분류기는 단일 모델을 데이터에 적합화하지 않고 그 대신 데이터를 연합으로 분류하는 모델의 앙상블을 구축한다.

• 앞 절과 동일한 X_train 훈련 데이터를 사용해 scikit-learn 앙상블 패키지에서 RandomForestClassifier()를 호출한다.
  

• 최적의 트리 수를 결정하기 위해 초매개변수 튜닝을 사용한다.

• 모델의 F1 점수를 확인한다.
  

• 클래스 수준 성능을 더 잘 이해하기 위해 혼동 행렬을 검사한다.
  

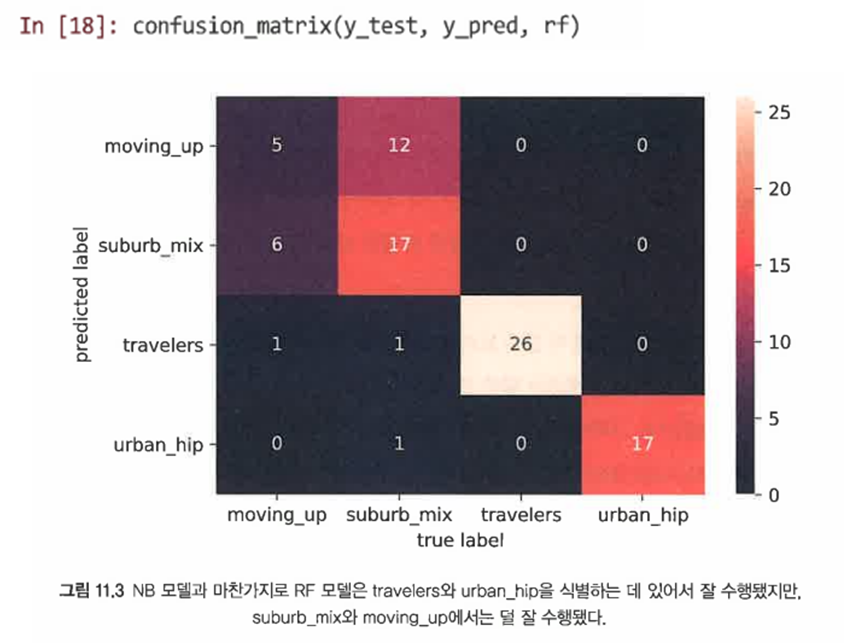
• 클래스별 정밀도와 재현율을 살펴본다.
  
  => NB 모델보다 조금 나쁘지만 유사하게 수행됐음을 알 수 있다.

11.1.3 랜덤 포레스트 변수 중요도

• RF 모델의 변수 중요도 평가 방법: 한 번에 하나의 변수에 대해 변수 값을 무작위로 순열하고 순열된 값을 사용해 OOB 데이터의 모델 정확도를 계산한 다음, 이를 실제 데이터와의 정확도와 비교한다.
• RF 모델의 featureimportances 매개변수에서 각 특징의 계산된 중요도를 볼 수 있다.
  
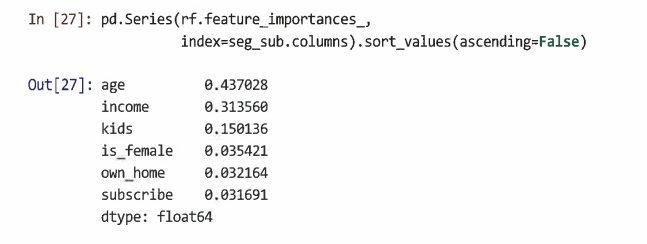
  => 연령과 소득은 의사결정 경계 시각화와 일치하는 가장 유용한 변수임을 알 수 있다.

11.2 예측: 잠재 고객 식별

• 분류의 또 다른 용도인 잠재 고객 예측

• 먼저 데이터를 훈련 샘플과 테스트 샘플로 나눈다.
  

• 훈련 집합의 구독자가 비구독자와 잘 차별화 되어있는가 확인해본다.
  

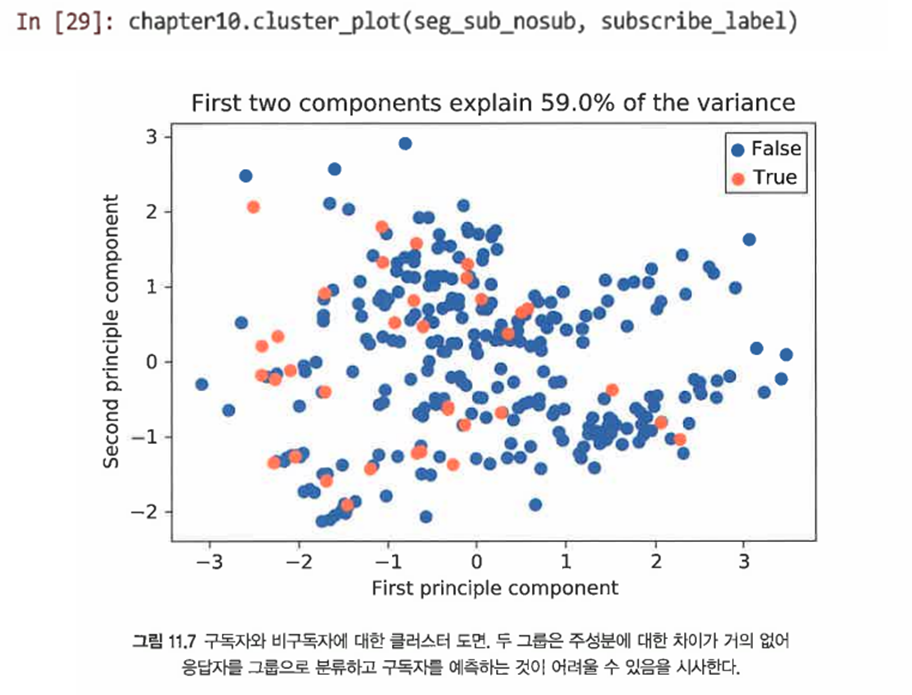
• 구독 예측을 위해 초기 RF 모델을 적합화한다.
  
  => 90%라는 정확도를 확인할 수 있다.

• 혼동행렬을 확인해본다.
  
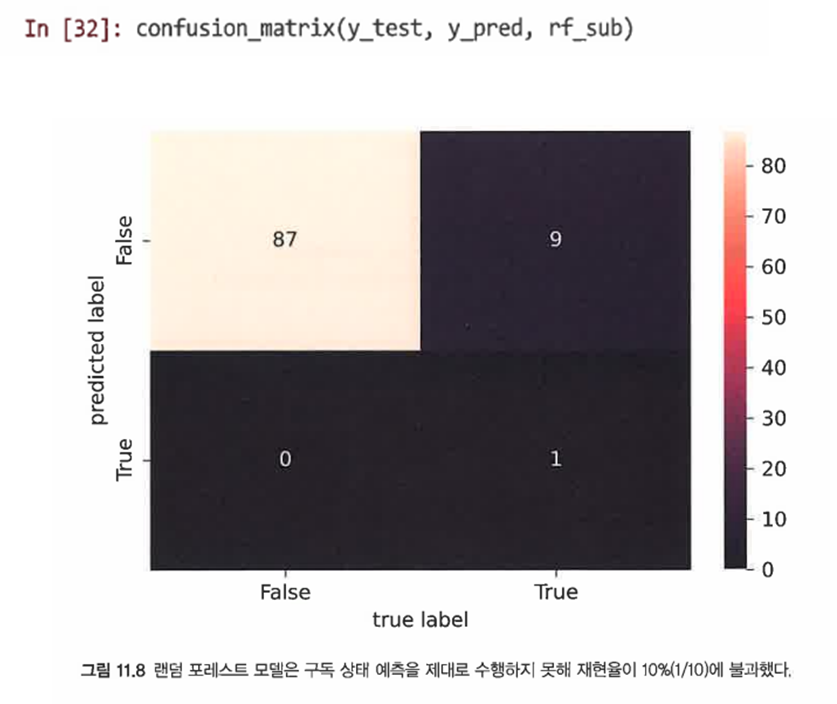
  => 오류율은 90.3%로 좋아보이지만, 재현율이 단 10%에 불과하다.

SOLUTION1. 초매개변수 튜닝: 점수 함수를 사용해 모델 매개변수 공간을 탐색해 최적으로 이어지는 매개변수를 식별한다. 최적을 찾기 위해 여러 매개변수 조합을 샘플링하는 그리드 검색을 수행할 수 있다.

• bestparams 매개변수를 사용해 최상의 점수 매개변수를 검사할 수 있다.
  
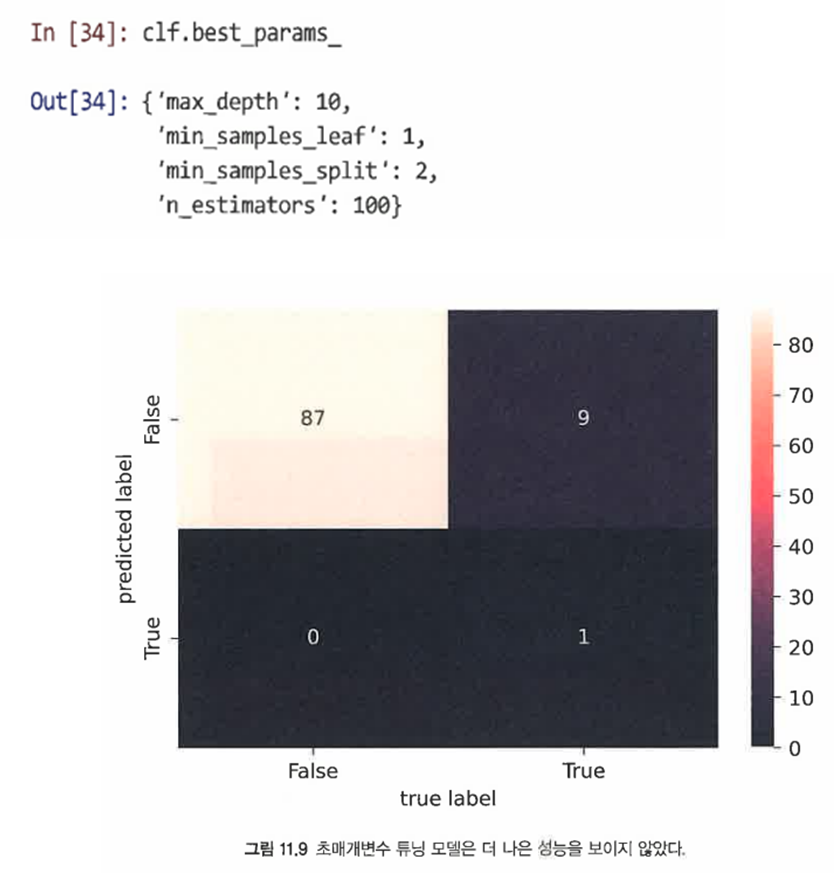
  => 그러나 초매개변수 튜닝을 해도 크게 성능이 향상되지는 않았음을 알 수 있다.

SOLUTION2. 다른 점수 함수 시도: 예를 들어 재현율을 점수 함수로 사용해본다.

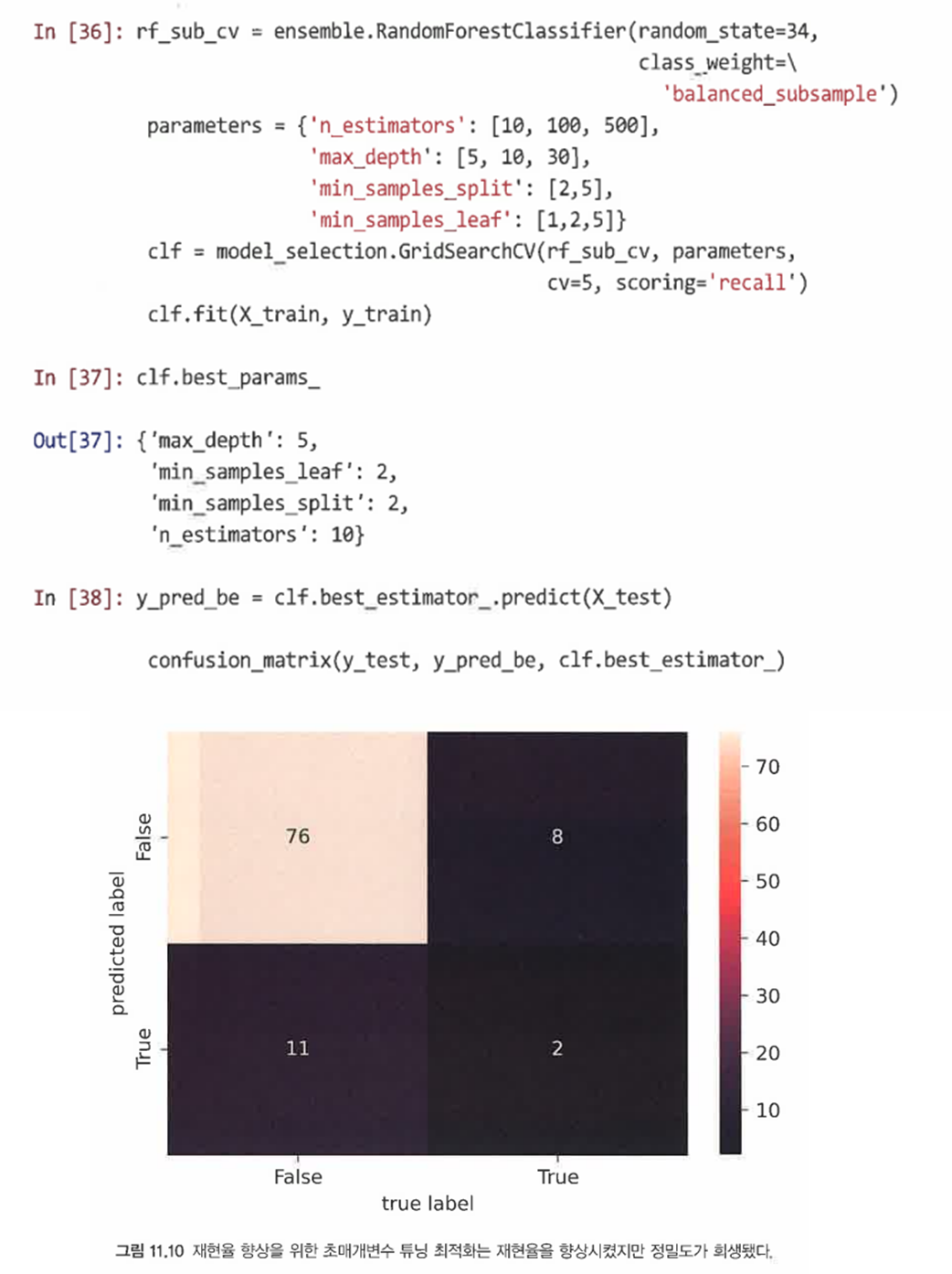
=> 여전히 그렇게 좋은 결과는 아니지만 그래도 변화가 있다.

SOLUTION3. 샘플 가중치: class_weight 매개변수를 사용해 희귀한 부류를 추가로 오버샘플링할 수 있다. 단, 과적합의 위험이 있다는 것이 단점이다.

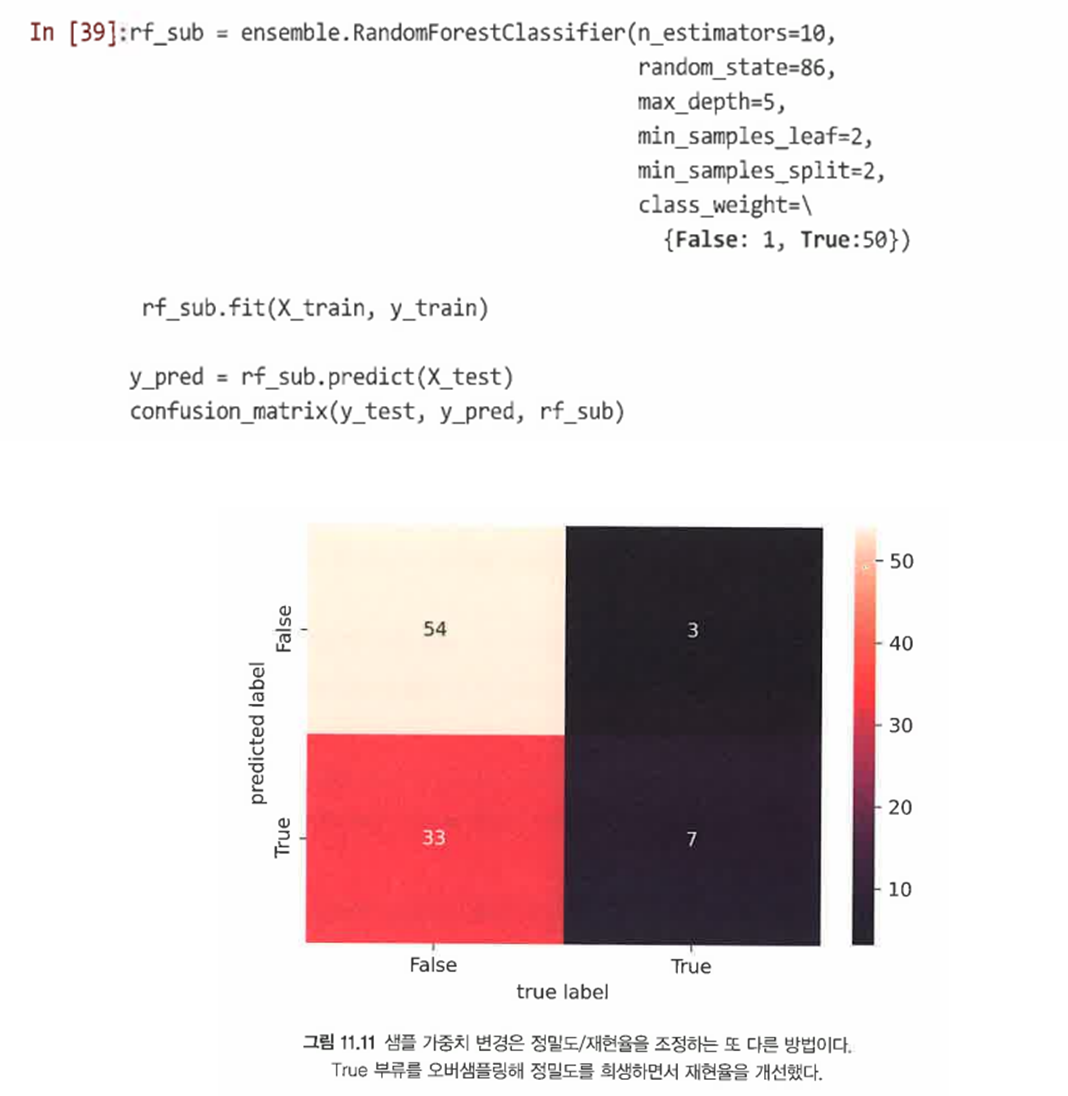
=> 효과적으로 성능이 향상됨을 볼 수 있다.

11.3 요점