데이터 복잡도 줄이기

9.1 소비자 브랜드 평가 데이터

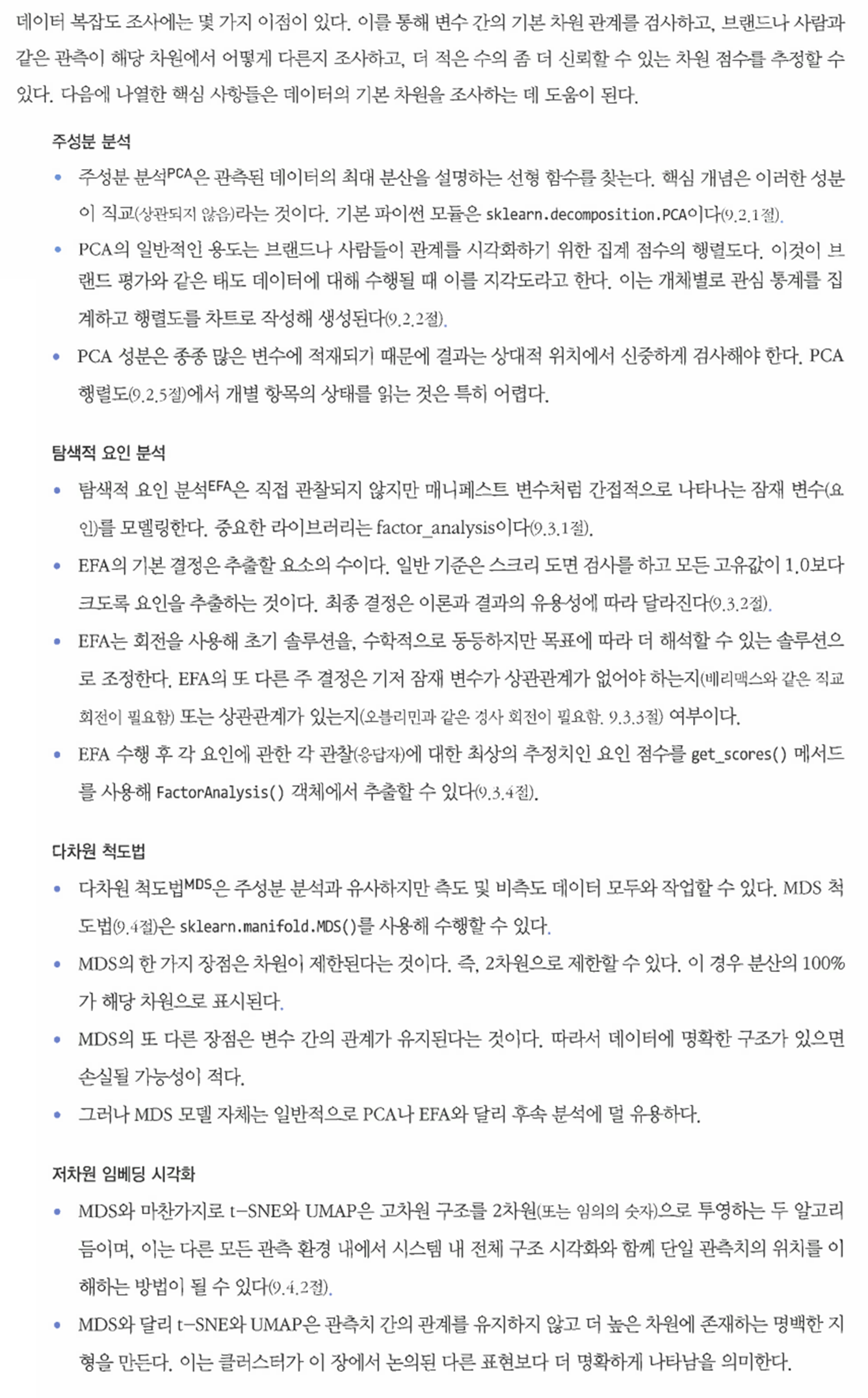
• 먼저 웹사이트로부터 데이터를 불러온다.
  
• 데이터 확인
  

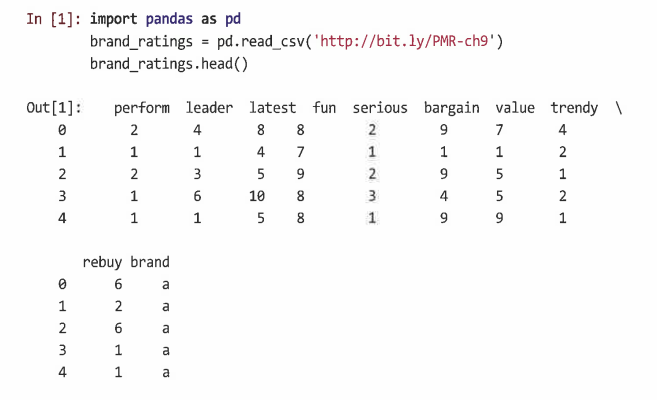
9.1.1 데이터 크기 조정
원시 데이터의 크기 조정을 통해 개임과 샘플 간에 데이터를 더 비교할 수 있다.

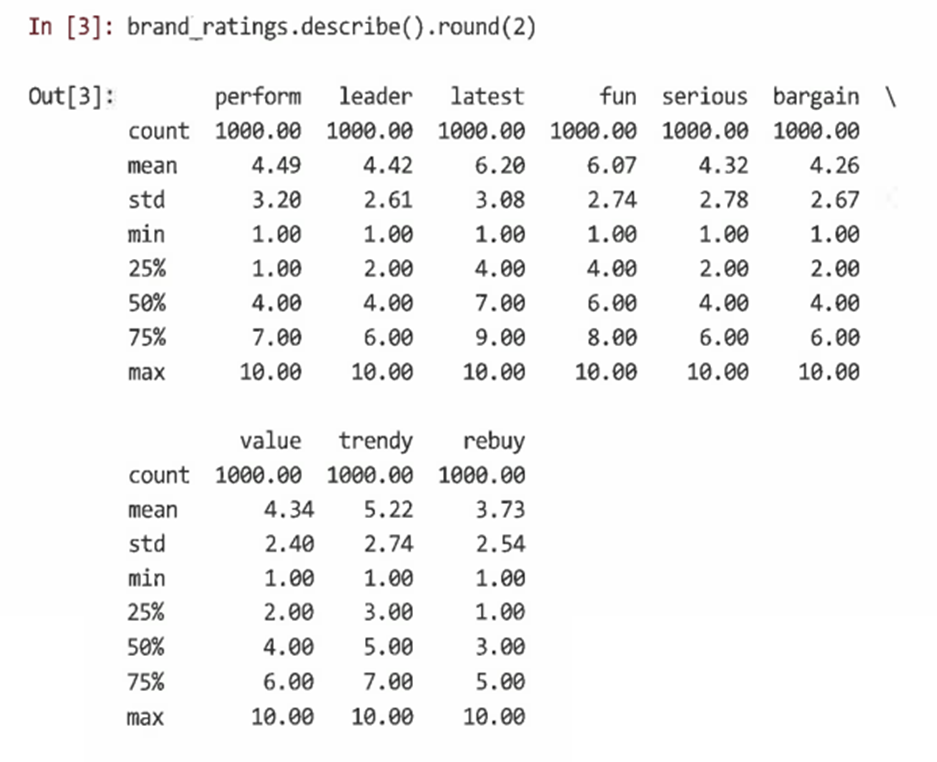
• 데이터 표준화(정규화, Z-점수): 모든 관측치에서 평균을 빼서 각 변수의 중심을 맞춘 다음 이러한 중심값을 표준편차 단위로 다시 조정하는 것
• sklearn.preprocessing.scale()을 사용해 한 번에 모든 변수의 크기를 조정할 수 있다.
  

9.1.2 속성 간의 상관관계
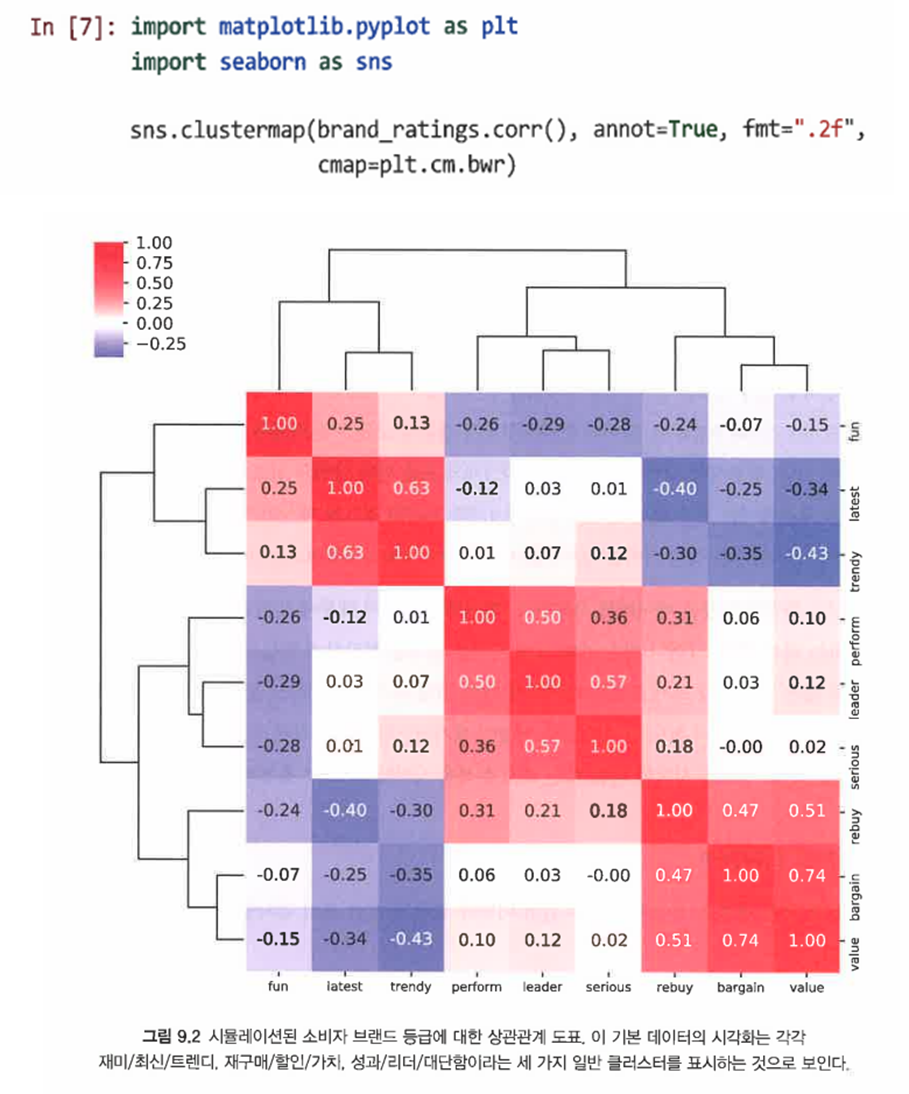
-corr()을 사용해 상관 행렬을 생성하고 변수 간의 이변량 검사를 위해 seaborn을 사용해 시각화한다.

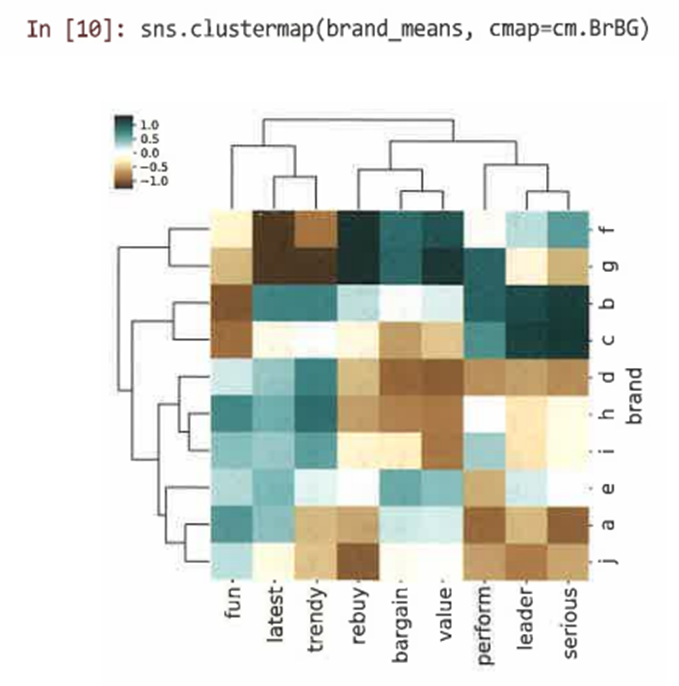
• heatmap() 대신 clustermap()을 사용해 계층적 클러스터 솔루션에서 변수의 유사성에 따라 행과 열을 재정렬한다.
  

9.1.3 브랜드별 종합 평균 등급

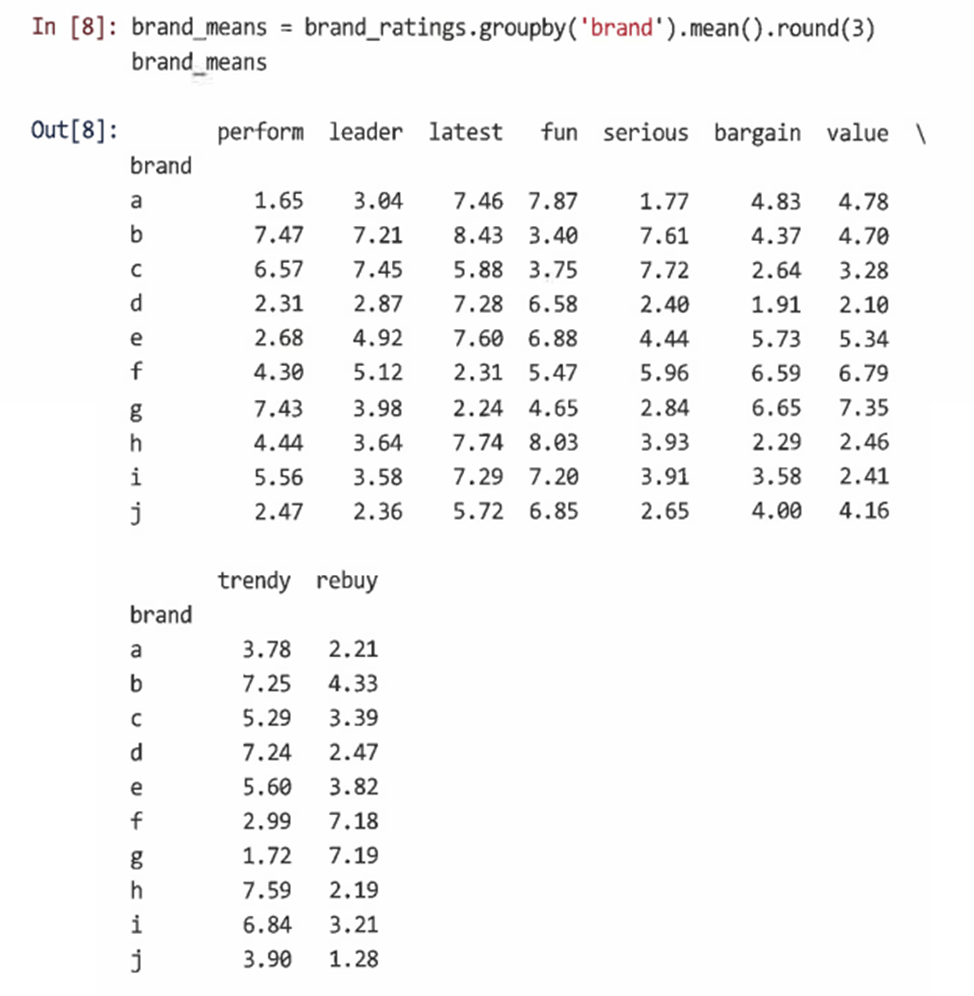
• "각 형용사에서 브랜드의 평균 위치는 무엇인가?"에 대한 답변을 groupby()를 사용해 각 브랜드별 변수 평균을 찾을 수 있다.
  
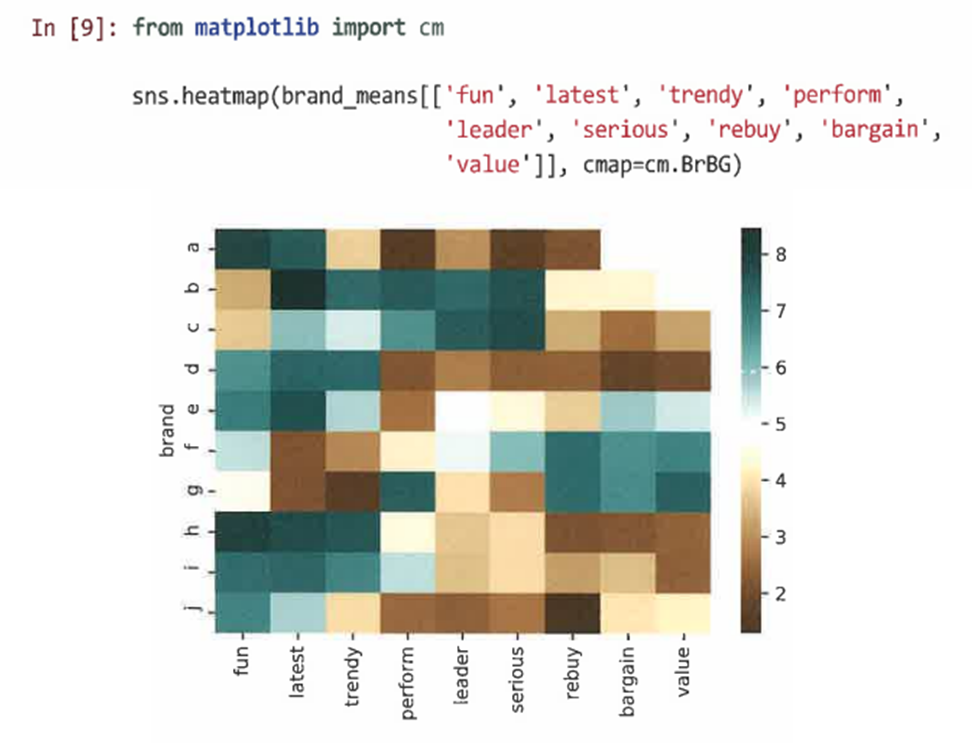
• heatmap()이나 clustermap()을 통해 이를 시각화한다.
  
  

9.2 주성분 분석과 지각도

주성분 분석(PCA): 데이터의 선형 관계를 포착하는 성분이라고 불리는 선형 방정식의 항으로 변수 집합을 재계산한다.

• 첫 번째 성분은 모든 변수에서 가능한 한 많은 분산을 단일 선형 함수로 포착한다.
• 두 번째 성분은 첫 성분 이후에 남아있는 가능한 많은 분산을 포착한다.

9.2.1 PCA 예

• 먼저 간단한 데이터셋으로 PCA를 탐색해 무슨 일이 일어나고 있는지에 대한 직관을 살펴보고 발전시킨다.

• 무작위 벡터 xvar를 새로운 벡터 yvar에 복사하고 데이터의 절반을 대체해 상관관계가 높은 데이터를 생성한다. 이 절차를 반복해 yvar에서 zvar를 만든다.
  

• swarmplot()을 사용해 동일한 값에 있는 포인트 수를 확인할 수 있도록 데이터를 시각화한다.
  
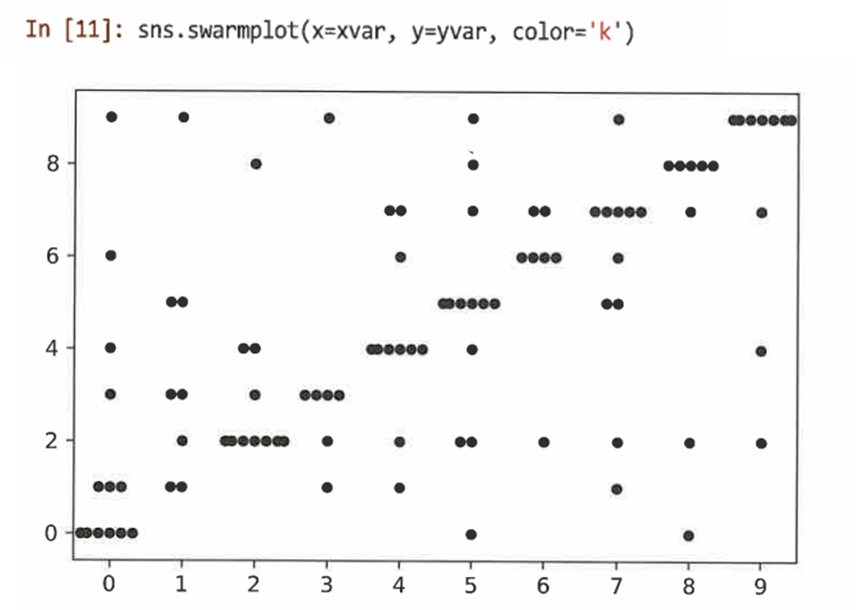
  => xvar는 yvar와 상관관계가 높다는 것을 확인할 수 있다.

• x,y,z var간의 상관관계를 확인한다.
  
  => xvar는 yvar와 상관관계가 높고, zvar와 상관관계가 적으며, yvar는 zvar와 강한 상관관계를 가짐을 알 수 있다.

• sklearn.decomposition 라이브러리의 PCA()를 이용해 PCA를 수행한다.
  
  => 첫 번째 성분은 설명 가능한 선형 분산의 62%를 차지하고, 두 번째 성분은 27%, 세 번째 성분은 11%를 차지함을 알 수 있다.

• 성분과 변수의 관계를 알아보기 위해 회전 행렬을 확인한다.
  
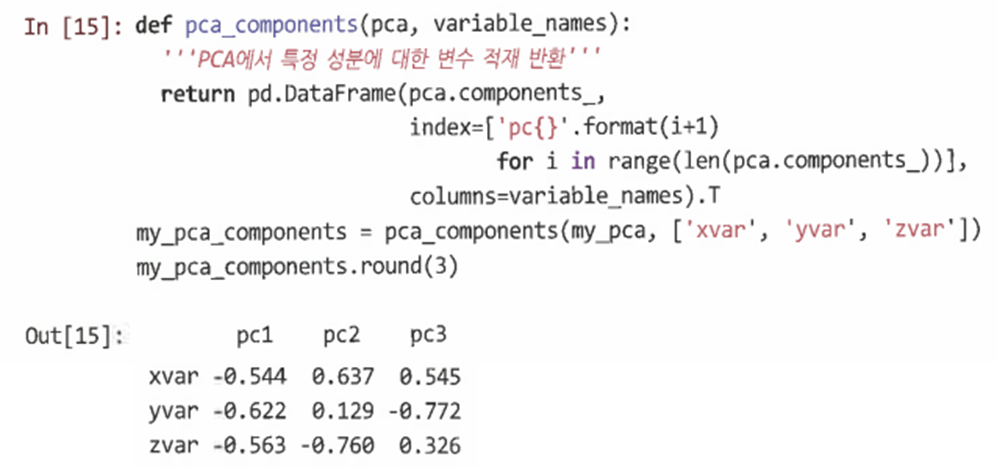
  => 성분1은 모두 같은 방향, 성분2는 x와 z이 서로 다른 방향, 성분3에서는 yvar를 제외한 다른 두 변수가 유사하고 yvar가 고유하다는 잔차 분산을 볼 수 있다.

9.2.2 PCA 시각화

• PCA의 결과를 효과적으로 조사하기 위해 행렬도를 생성할 수 있다.
  
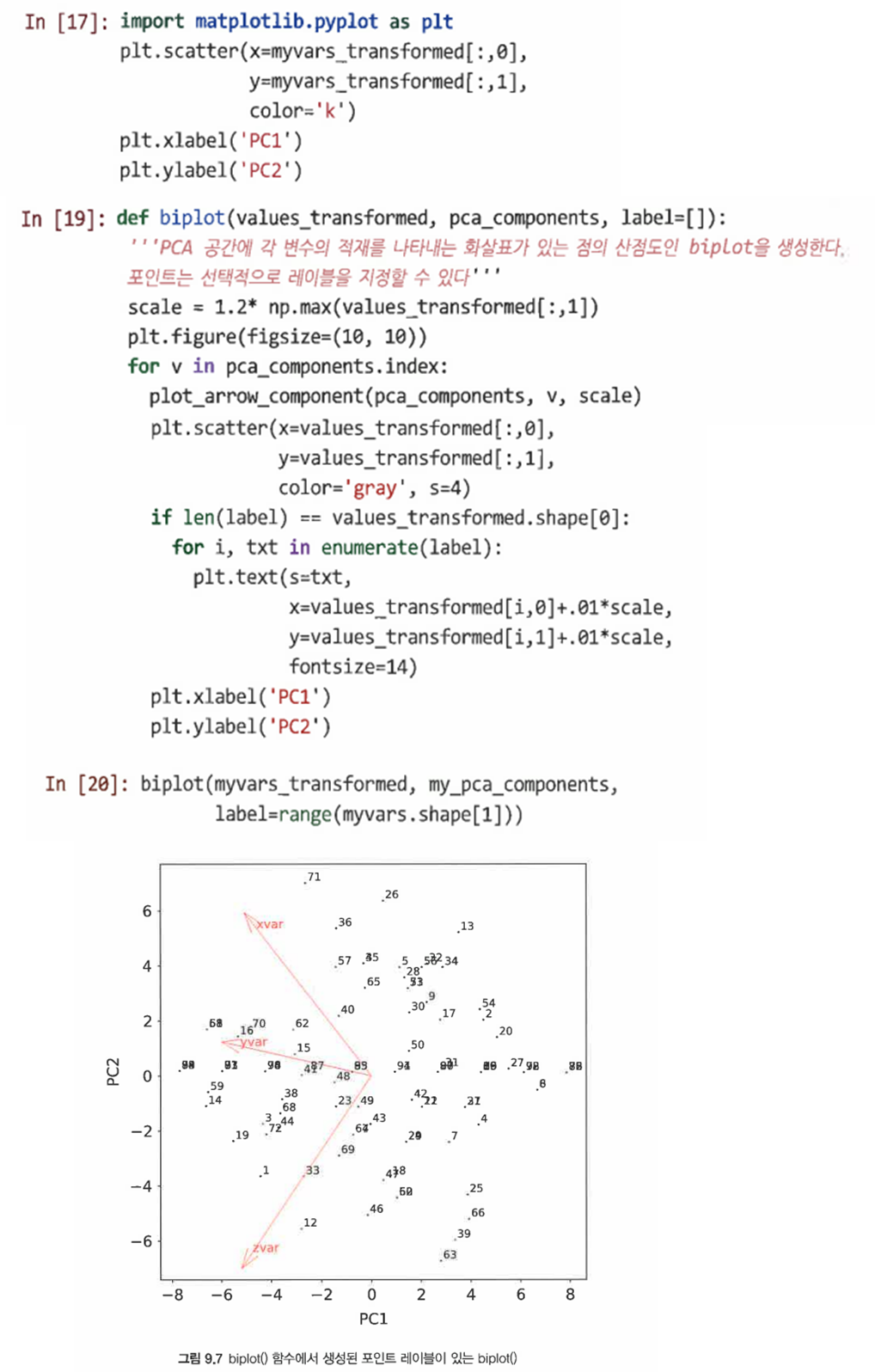
  => 주성분에 대한 각 변수의 최적 적합을 보여주는 화살표를 확인할 수 있다

9.2.3 브랜드 평가를 위한 PCA

• 새로운 변수를 생성하고 pca_summary() 함수를 사용해 각 성분에 포함된 분산을 확인할 수 있다.
  
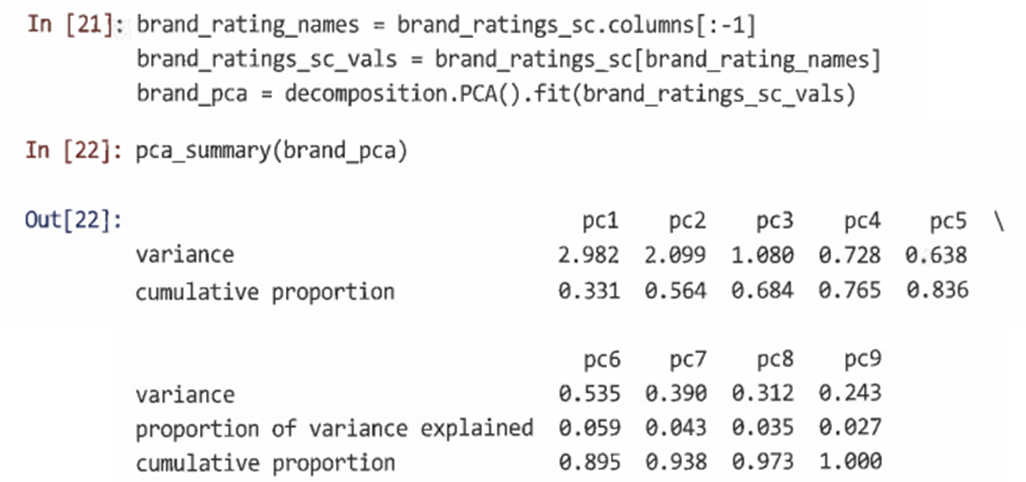
• PCA를 분석할 때 중요한 도면은 각 성분이 추가하는 추가 분산의 연속적인 비율을 보여주는 스크리 도면이다.
  
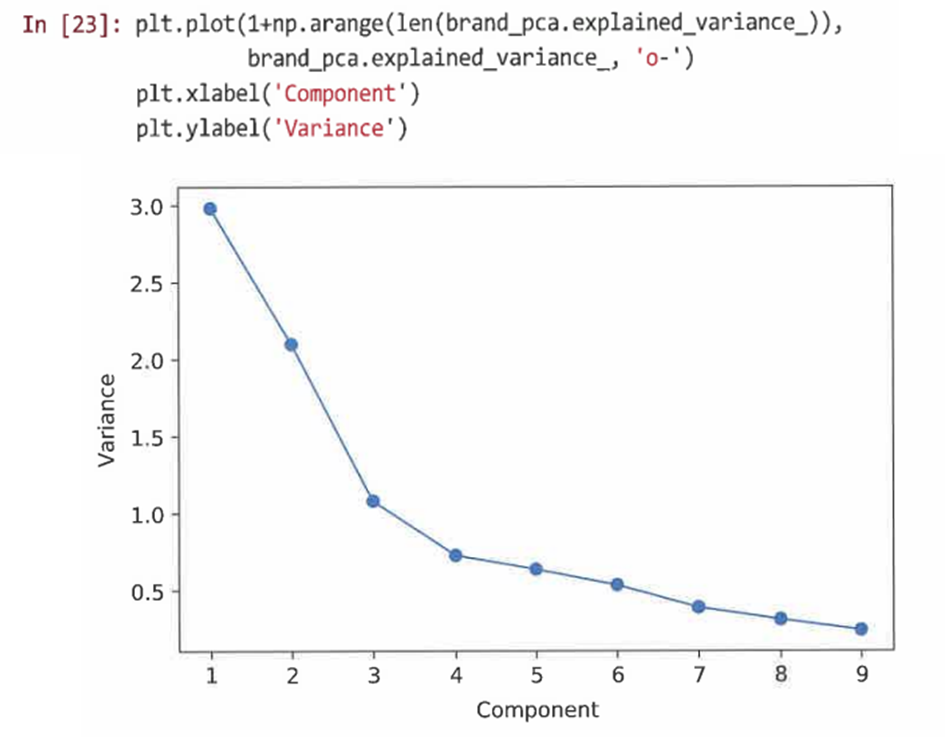
• 이전 절의 여러 헬퍼 함수를 사용해 등급 형용사가 어떻게 연관돼 있는지 보여주는 처음 두 주성분의 행렬도를 도식화할 수 있다.
  
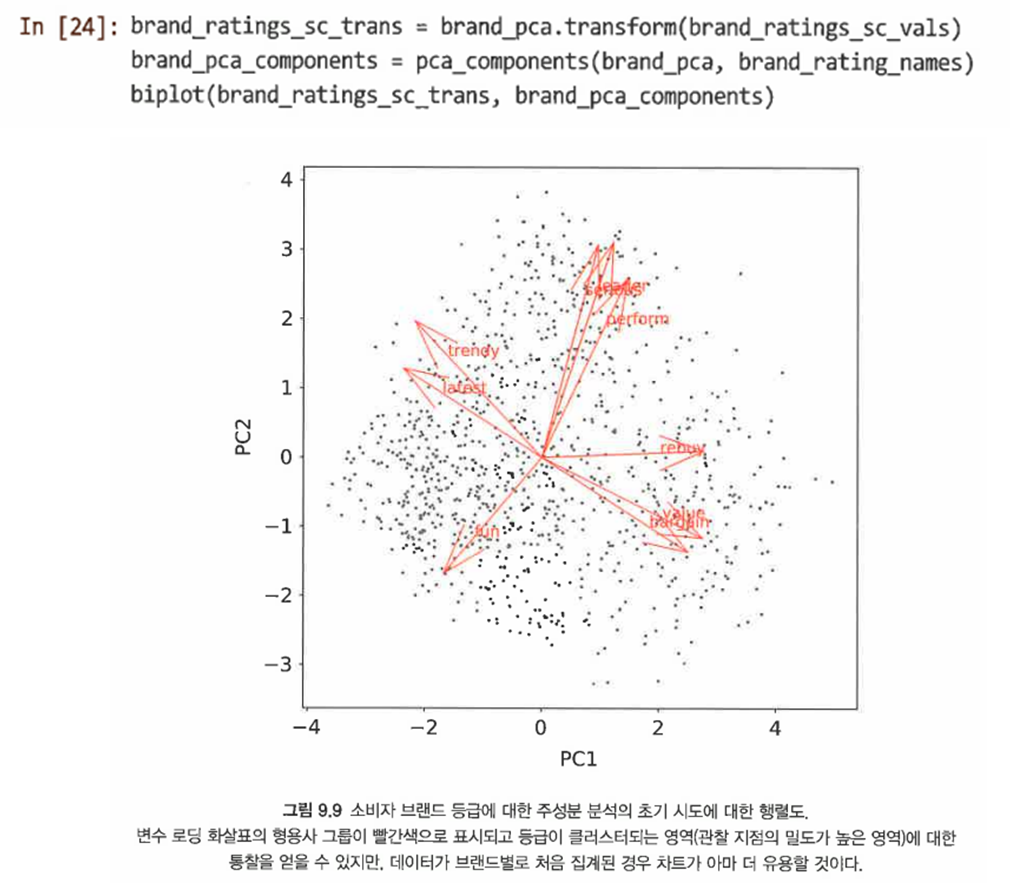
• 그러나 이러한 도면이 너무 조밀하고 브랜드 위치에 대해서는 알려주는 바가 없다는 단점이 존재한다.

9.2.4 브랜드의 지각도

• 먼저 groupby()를 사용해 위에서 찾은 브랜드별로 각 형용사의 평균 등급을 구성한다.
  

• PCA로 변환된 평균 등급의 행렬도는 처음 2개의 주성분과 관련한 브랜드의 위치를 보여주는 해석 가능한 지각도를 제공한다.
  
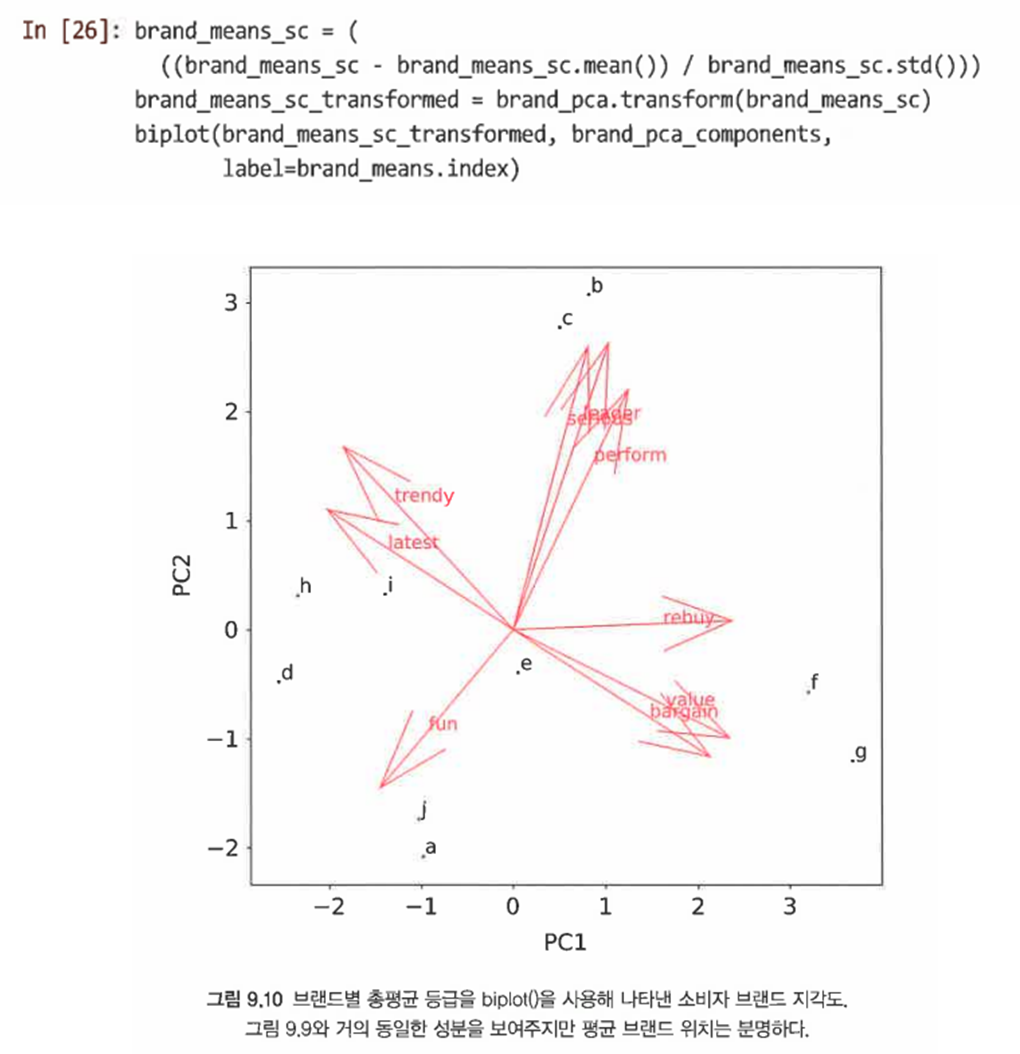
  => 이를 통해 데이터에 대한 질문과 답변을 내릴 수 있다. 기업의 전략적 목표에 따라 어떻게 브랜드를 포지셔닝할 것인지 살펴볼 수 있다. (특정 브랜드와 비슷한 방향으로 가기 위해서는 어떻게 해야하는지, 어떤 브랜드도 자리잡지 않은 차별화된 공간을 지향할 것인지)

• Q1. 브랜드 E와 C의 차이에 대해 알고자 한다면?
  
  => E가 '할인'과 '재미'에서 C보다 상대적으로 강하다는 것을 보여준다.

• Q2. 위치를 지정하는 방법은?
  격차가 해당 4개 브랜드의 평균을 대략적으로 반영한다고 가정할 때, 브랜드 행의 평균을 찾은 다음 E와의 차이를 취함으로써 구할 수 있다.
  
  => 이는 E가 '최신'과 '재미'에 대한 강조를 줄이면서 성과에 대한 강조를 증가시킴으로써 격차를 타깃으로 할 수 있음을 의미한다.

• 여러 차원에서 여러 브랜드를 비교하려는 경우 데이터의 변동을 설명하는 처음 2~3개의 주성분에만 집중하면 도움이 될 수 있다.

• 각 주성분이 데이터의 변동을 얼마나 설명하는지 보여주는 스크리 그림을 사용하면 집중할 성분 수를 선택할 수 있다.

9.2.5 지각도에 대한 주의
주의사항1. 집계 수준과 유형을 신중하게 선택해야 한다. 집계도를 해석하기 전에 전체 데이터와 집계 데이터의 차원이 유사한지 확인해야 한다.

주의사항2. 관계는 엄격하게 제품 범주와 테스트되는 브랜드 및 형용사와 관련이 있다. 즉, 새로운 브랜드가 시장에 진입하면 위치가 크게 바뀔 수 있음을 유의해야 한다.

주의사항3. 단일 형용사에 대한 브랜드의 강점을 차트에서 직접 읽을 수 없다. 위치는 절대적이지 않은 상대적인 것이다.

9.3 탐색적 요인 분석

탐색적 요인 분석(EFA): 설문조사와 심리평가에서 구성체 사이의 관계를 평가라는 기술군.

9.3.1 기본 EFA 개념
-요인 행렬과 원시 변수와의 관계.
-PCA와는 달리 매니페스트 변수 측면에서 최대한 해석 가능한 솔루션을 찾으려고 한다.
-일반적으로 각 요인에 대해 소수의 적재는 매우 높고 해당 요인에 대한 다른 적재는 낮은 솔루션을 찾으려고 한다.

• EFA는 세 가지 넓은 의미에서 데이터 축소 기술로 사용된다:

1. 차원 축소의 기술적 의미에서 더 큰 항목 집합 대신 요인 점수를 사용할 수 있다.
2. 불확실성을 줄일 수 있다.
3. 관심 요인에 높은 기여를 하는 것으로 알려진 항목에 초점을 맞춰 데이터 수집을 줄일 수 있다.

9.3.2 EFA 솔루션 찾기

• 먼저 추정할 요인의 수를 결정하기 위해 스크리 도면 또는 고유값을 사용할 수 있다.
  
  => 고유값을 확인했을 때, 처음 3개의 고유값은 1.0보다 크다는 것을 볼 수 있다.
• EFA의 모범 사례는 요인 솔루션 확인을 통해 추려낼 수 있다. sklearn의 요인 분석 모듈 sklearn.decomposition.FactorAnalysis()를 사용한다.
  
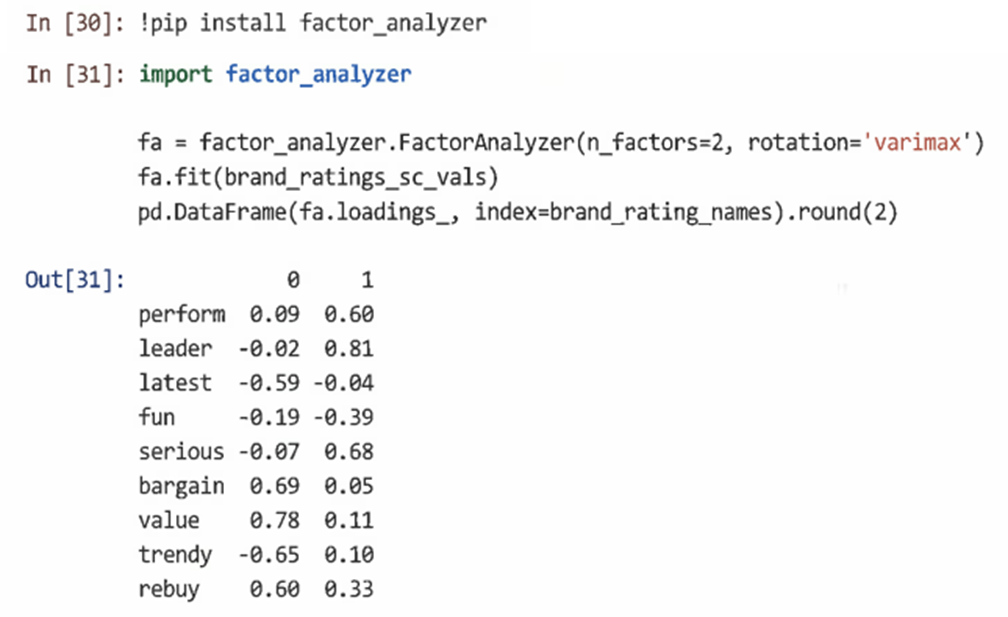
  => 2요인 솔루션에서 요인 0은 '할인'과 '가치'에 강하게 적재되므로 '가치'로 해석될 수 있으며, 요소 1은 '리더'와 '대단함' 요소에 적재되므로 '카테고리 리더' 요소로 간주될 수 있다.

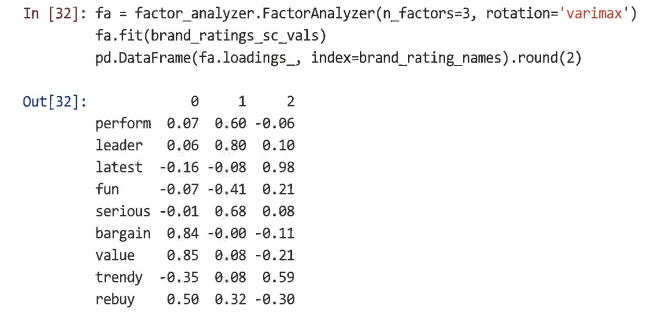
=> 3요인 솔루션은 '가치'와 '리더' 요소를 유지하고 '최신' 및 '트렌디'에 강하게 적재되는 명확한 '최신' 요소를 추가한다.

9.3.3 EFA 로테이션

• 일반적으로 기본값은 상관관계가 0인 요인을 찾는 것이다(varimax 회전 사용). EFA는 기본 차원에 중점을 두는 반면 PCA는 데이터의 차원 변환에 중점을 둔다.

• 그러나 상관 요인을 허용할 수도 있다. => 비스듬한 회전(rotation='oblimin')
  

• 추정된 잠재 요인 간의 관계를 보여주는 요인 상관 행렬을 확인할 수 있다.
  
  => 요인1(가치)은 요인3(최신)과 음의 상관관계(r=-0.41)가 있으며, 본질적으로 요인2와는 상관관계가 없다(r=0.13).

• 클러스터 맵을 사용해 항목 요소 관계를 시각화할 수 있다.
  

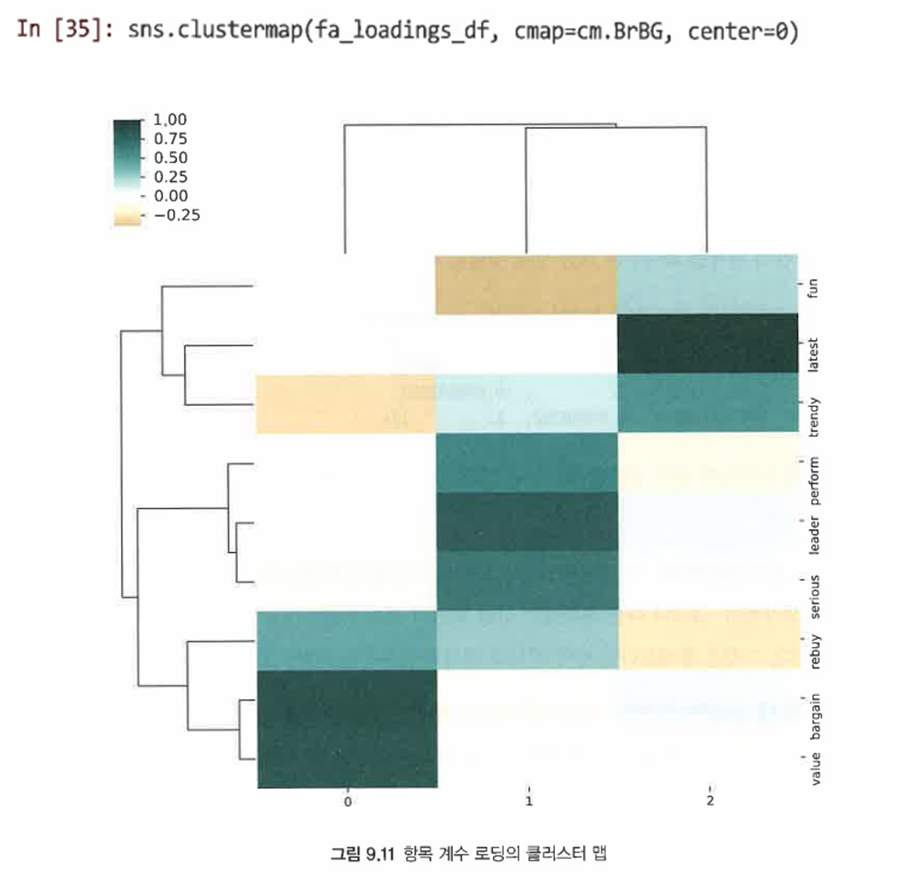
9.3.4 브랜드에 요인 점수 사용

• 요인 구조를 추정하는 것 외에도 EFA는 각 관찰에 대한 잠재 요인 점수를 추정한다.

• 요인 점수는 transform() 메서드를 사용해 FactorAnalyzer() 객체에서 계산하며 별도의 데이터프레임으로 저장할 수 있다.
  
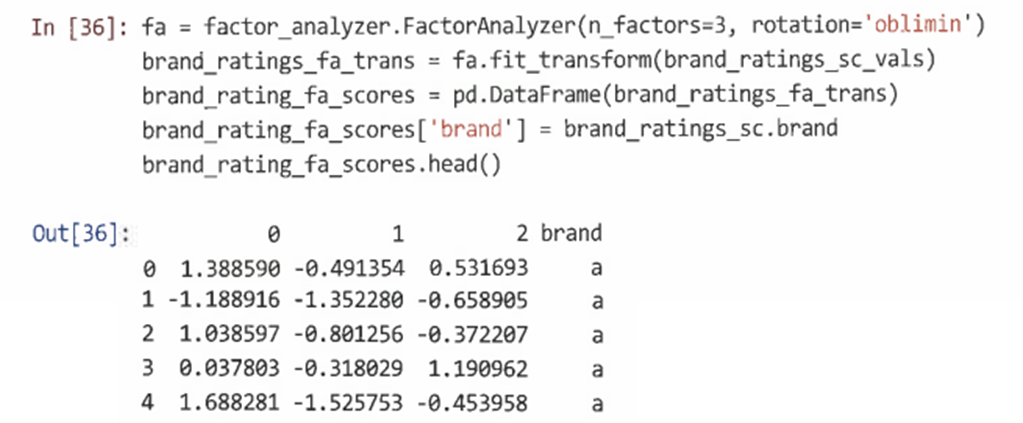
  => 결과는 각 요인과 브랜드에 대한 각 응답자의 추정 점수이다.

• 브랜드의 전체적인 위치를 찾기 위해 groupby()를 사용해 브랜드별로 개별 점수를 집계한다.
  

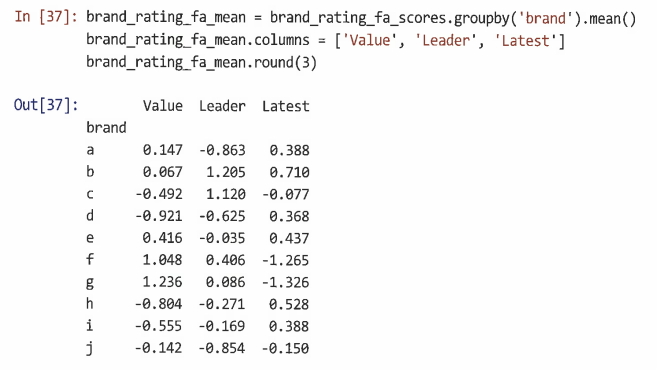
• 클러스터 맵을 통해 브랜드별 점수를 그래프로 표시한다.
  

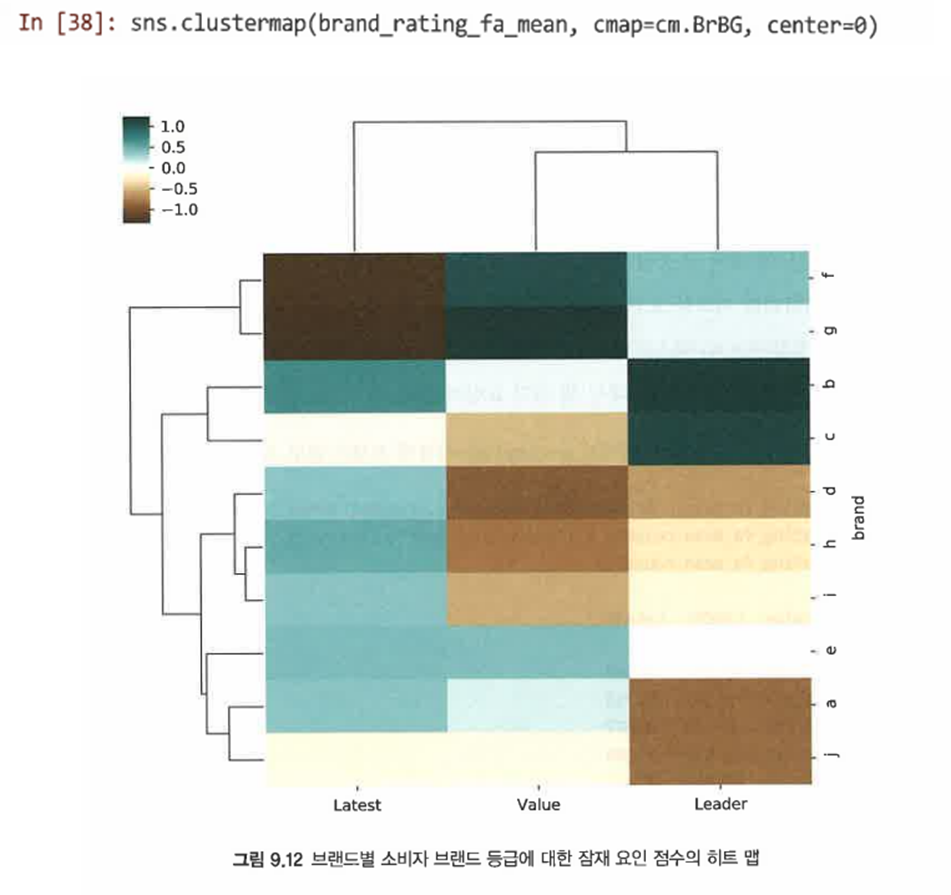
=> 이처럼 항목이 기본 구성체와 관련된 경우 EFA는 변수를 집계해 더 간단하고 해석가능한 잠재 변수를 생성함으로써 데이터 복잡성을 줄인다.

9.4 다차원 척도법

다차원 척도법(MDS): 데이터의 저차원 표현을 찾는데도 사용할 수 있는 제품군.

• 거리 행렬(유사성 행렬)을 사용하여 항목 간에 관찰된 모든 유사성을 가장 잘 보존하는 저차원 지도를 찾으려고 한다.
  

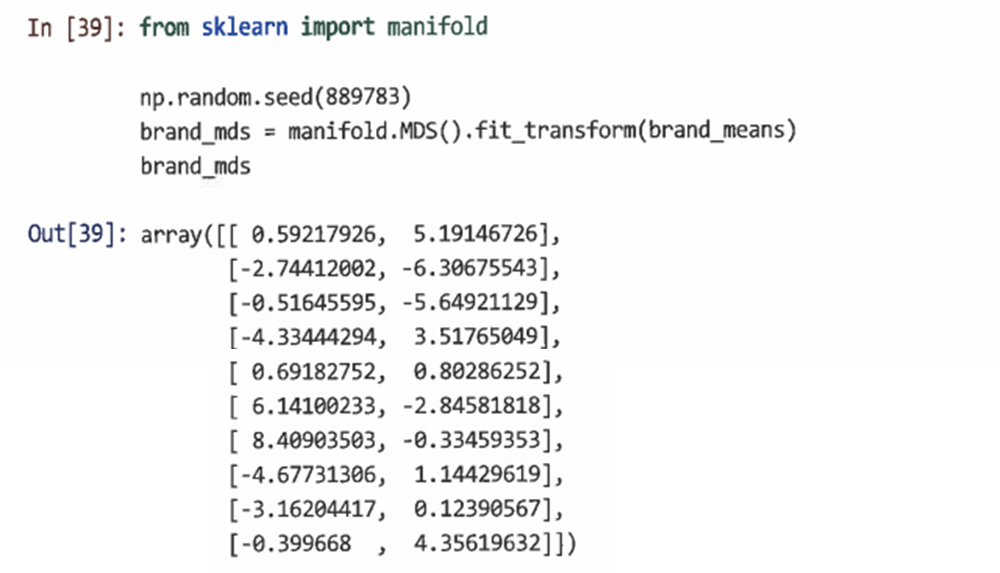
• MDS.fit_transform()의 결과를 좌표로 두고 scatter()하면 다음과 같이 시각화할 수 있다.
  

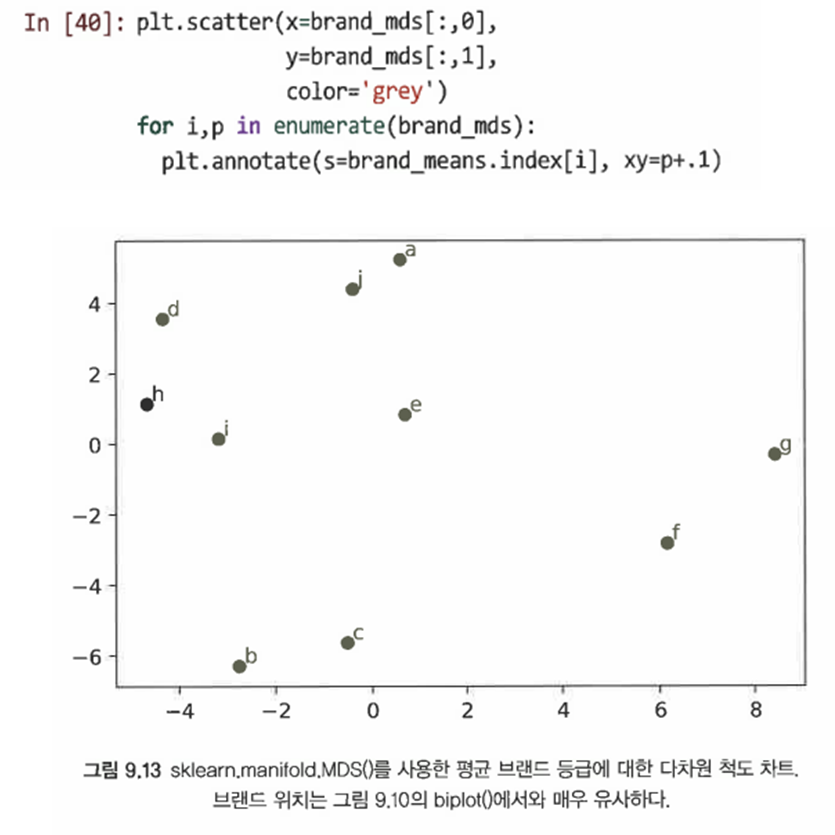
9.4.1 비측도 MDS

• 순위나 범주형 변수와 같은 비측도 데이터의 경우 sklearn.manifold.MDS()를 인스턴스화할 때 metrics=False 인수를 전달하기만 하면 된다.

9.4.2 저차원 임베딩을 사용한 시각화
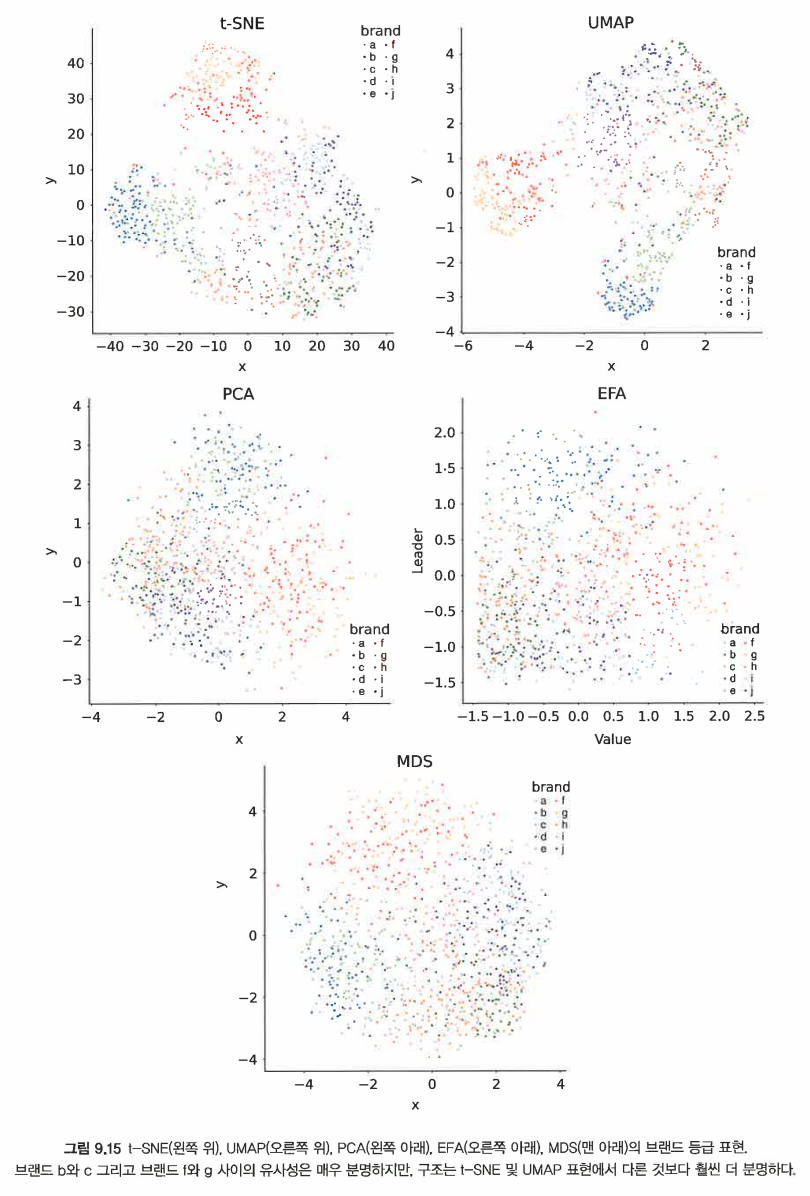
다음과 같은 비선형 차원 축소 도구를 이용해 고차원의 데이터를 시각화할 수 있다.

• t-SNE
  

• UMAP
  
  => UMAP은 더 빠르고 클러스터를 더 '축소'하는 경향이 있다.

• 다양한 분석도 조사 방법의 비교
  

9.5 요점