연속 변수 간의 관계
4.1 소매 데이터
4.1.1 데이터 시뮬레이션
-
매장과 온라인에서 제품을 판매하는 다채널 소매 업체의 1000명 고객에 대한 데이터셋 생성
-
프로세스를 재현할 수 있도록 난수 시드 설정

-
고객을 설명하는 여러 변수를 만들 후 해당 변수를 cust_df 데이터프레임에 추가
-
고객의 연령은 numpy.random.normal(loc, scale, size)를 사용해 평균 35, 표준 편차 5인 정규분포에서 추출
-
기본 CRM 데이터의 최종 변수는 distance_to_store이며 정규 분포의 지수를 따른다고 가정

4.1.2 온라인 및 내점 판매 데이터 시뮬레이션
-온라인 방문과 거래에 대한 각 고객의 1년 총액과 총지출액을 더해 온라인 상점에 대한 데이터 생성
-
시간에 따른 이벤트 수를 모델링하는데 자주 사용되는 이산 분포인 음이항 분포로 방문 수 시뮬레이션: numpy.random.negative_binomial(n, p , size)를 사용해 생성
-
n은 목표 성공 횟수, p는 단일 성공 확률
-
이메일이 있는 고객에 대해 평균 15회의 온라인 방문을 추가((cust_df.email=='yes')*15)
-
마지막으로 표본 중앙값에 상대적인 고객 연령을 기준으로 목표 평균에서 방문 수를 더하거나 뺀다 => 이 방법을 통해 어린 고객은 더 많은 온라인 방문으로 시뮬레이션 실행 가능

-
각 온라인 방문마다 주문 확률이 30%라고 가정하고 numpy.random.binomial()을 사용해 online_trans 변수 생성
-
금액은 로그 정규 분포를 따른다고 가정

-
같은 방법으로 매장 내 판매 데이터도 생성
-
거래가 음의 이항 분포를 따르고 먼 속에 사는 고객의 평균 방문 수가 더 낮다고 가정

-
데이터 검토
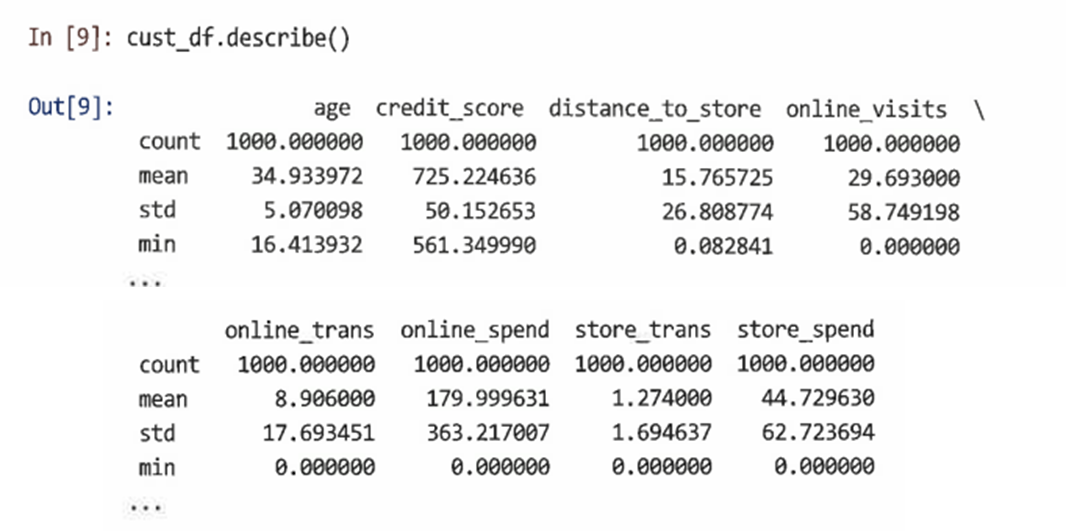
4.1.3 만족도 조사 응답 시뮬레이션
-
일부 고객에 대한 설문 조사 데이터 생성
-
각 고객의 모든 브랜드에 대한 만족도는 관찰할 수 없다고 가정
-
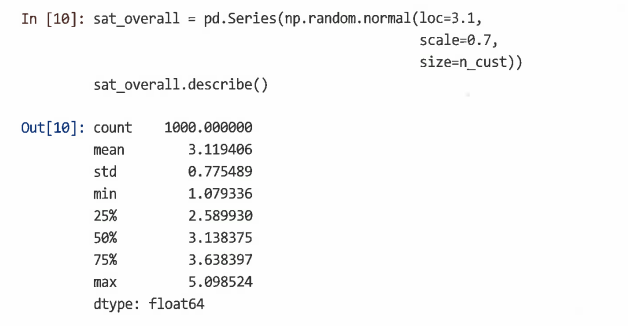
설문 조사 항목에 대한 고객의 응답은 전반적으로 관찰되지 않은 만족도(halo)와 서비스 및 제품에 대한 특정 만족도 수준을 기반으로 한다고 가정
-
halo 변수에서 이러한 점수를 생성하기 위해 numpy.random.normal()을 사용해 추출된 항목에 특정한 임의 값 sat_overall을 추가
-
설문 조사 응답은 일반적으로 불연속적인 순서 척도로 제공되기 때문에 numpy.floor() 함수를 사용해 연속 임의 값을 불연속 정수로 변환
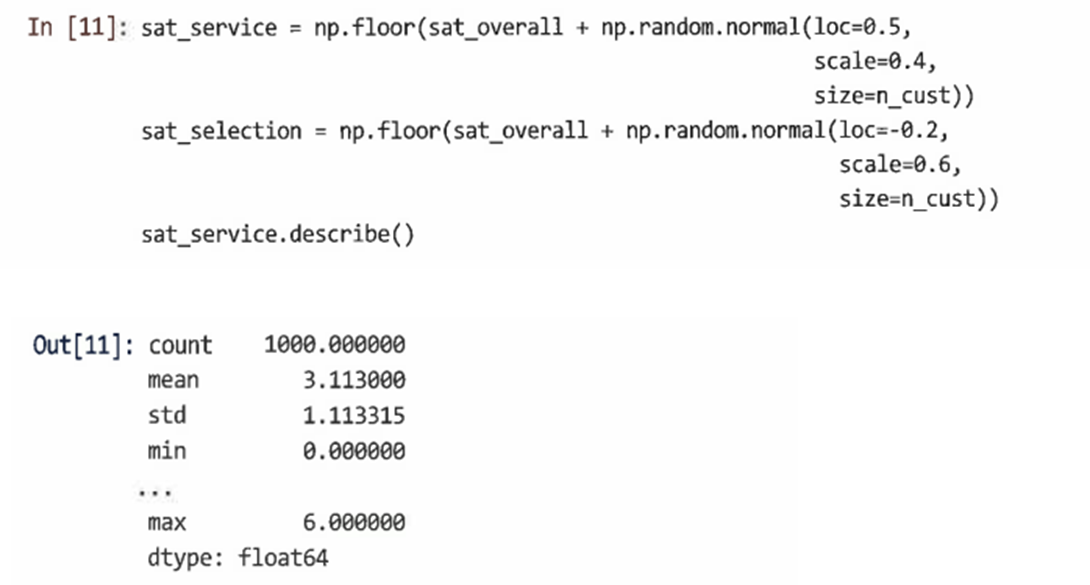
-
일반적인 설문 조사는 5점 척도로 주어지기 때문에 이에 맞푸어 상한값과 하한값 조정
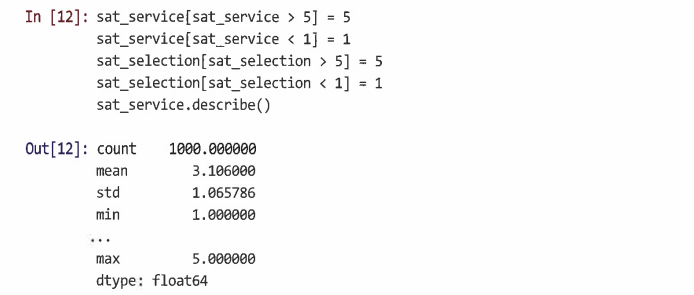
4.1.4 무응답 데이터 시뮬레이션
-
일부 고객은 설문 조사에 응답하지 않기 때문에 무응답으로 모델링된 하위 집합에 대해서는 시뮬레이션 답변 제거
-
no_response가 True인 고객의 설문 응답에 numpy.nan값을 할당
-
여기서는 고령 고객일수록 무응답의 가능성이 더 높다고 설정
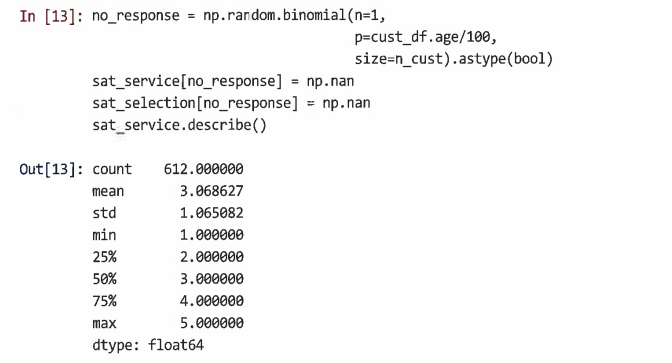
-
마지막으로 cust_df에 설문 조사 응답 추가
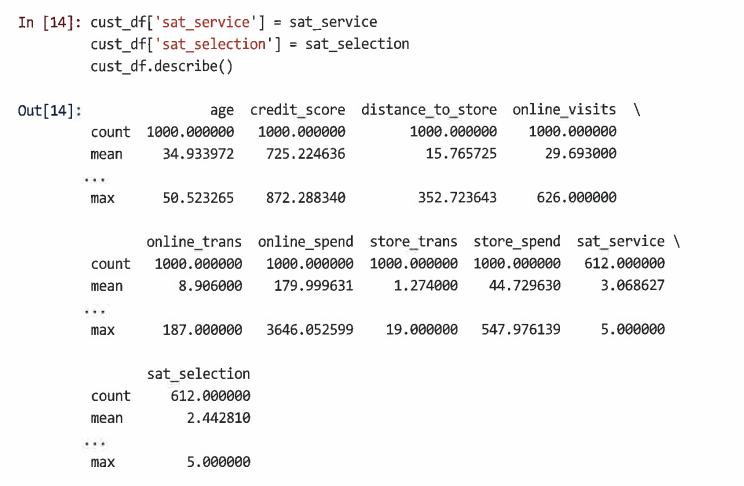
4.2 산점도가 있는 변수 간의 연관성 탐색
- 먼저 head() 및 dtypes로 데이터프레임 확인 및 구조 검토
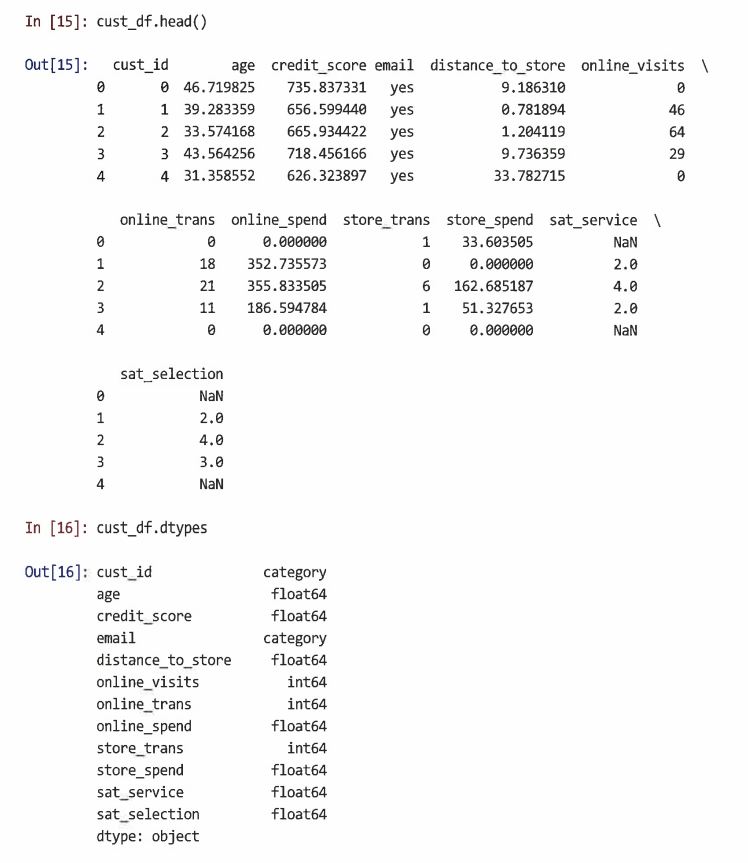
4.2.1 plot()을 사용해 기본 산점도 만들기
-
matplotlib를 사용해 plot() 데이터프레임 메서드를 통해 각 고객의 연령과 신용 점수 간의 관계 탐색
-
이 경우 kind='scatter'와 x값을 지정해 연령과 y값을 credit_score로 나타낸다
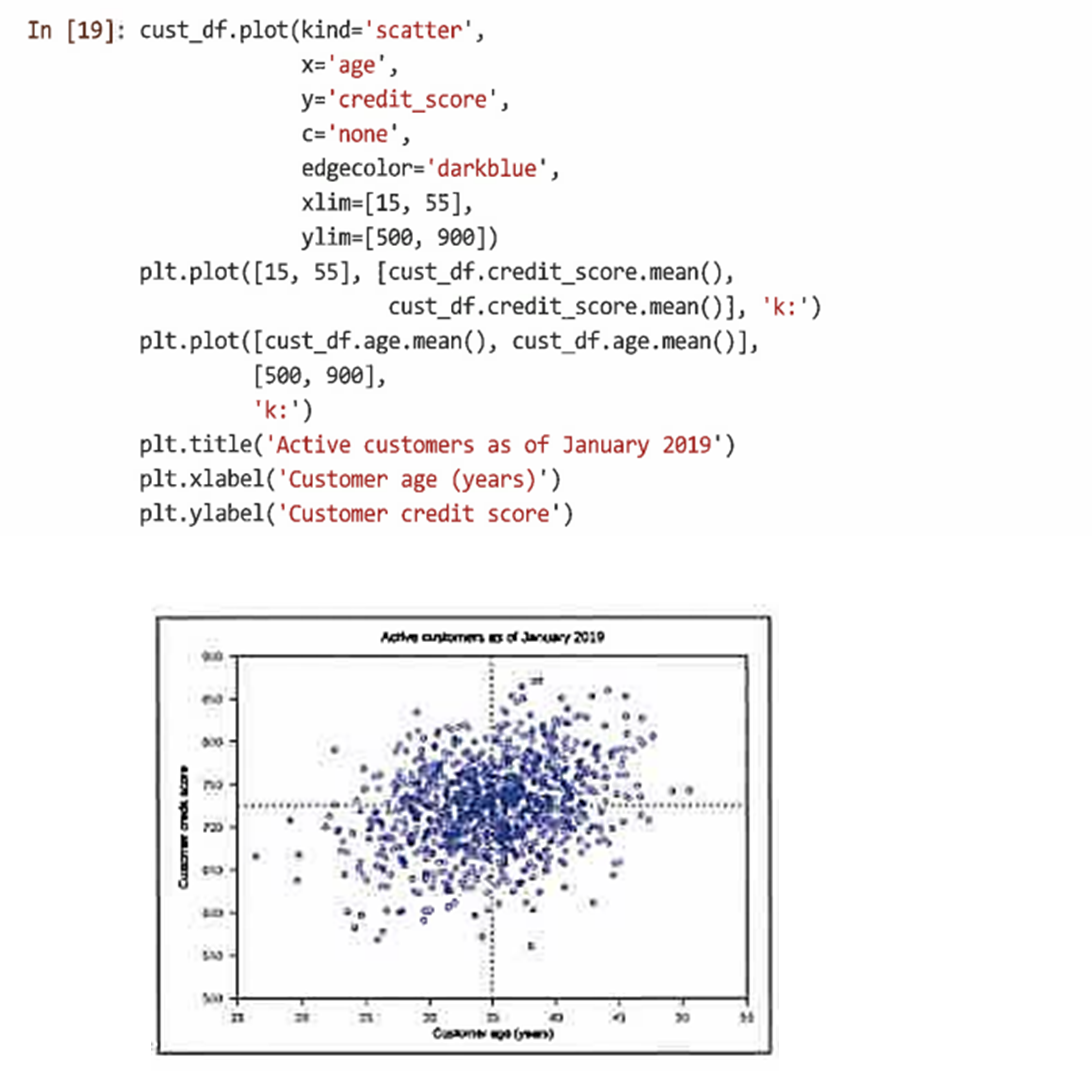
-
온라인 판매와 매장 판매 비교하기
-
점을 더 명확하게 볼 수 있도록 s=8 인수를 사용해 점 축소
-
두 채널 중 하나에서 아무것도 구매하지 않은 많은 고객과 채널 중 하나에서 상당히 많은 양을 구매하는 적은 수의 고객이 있음을 보여줌
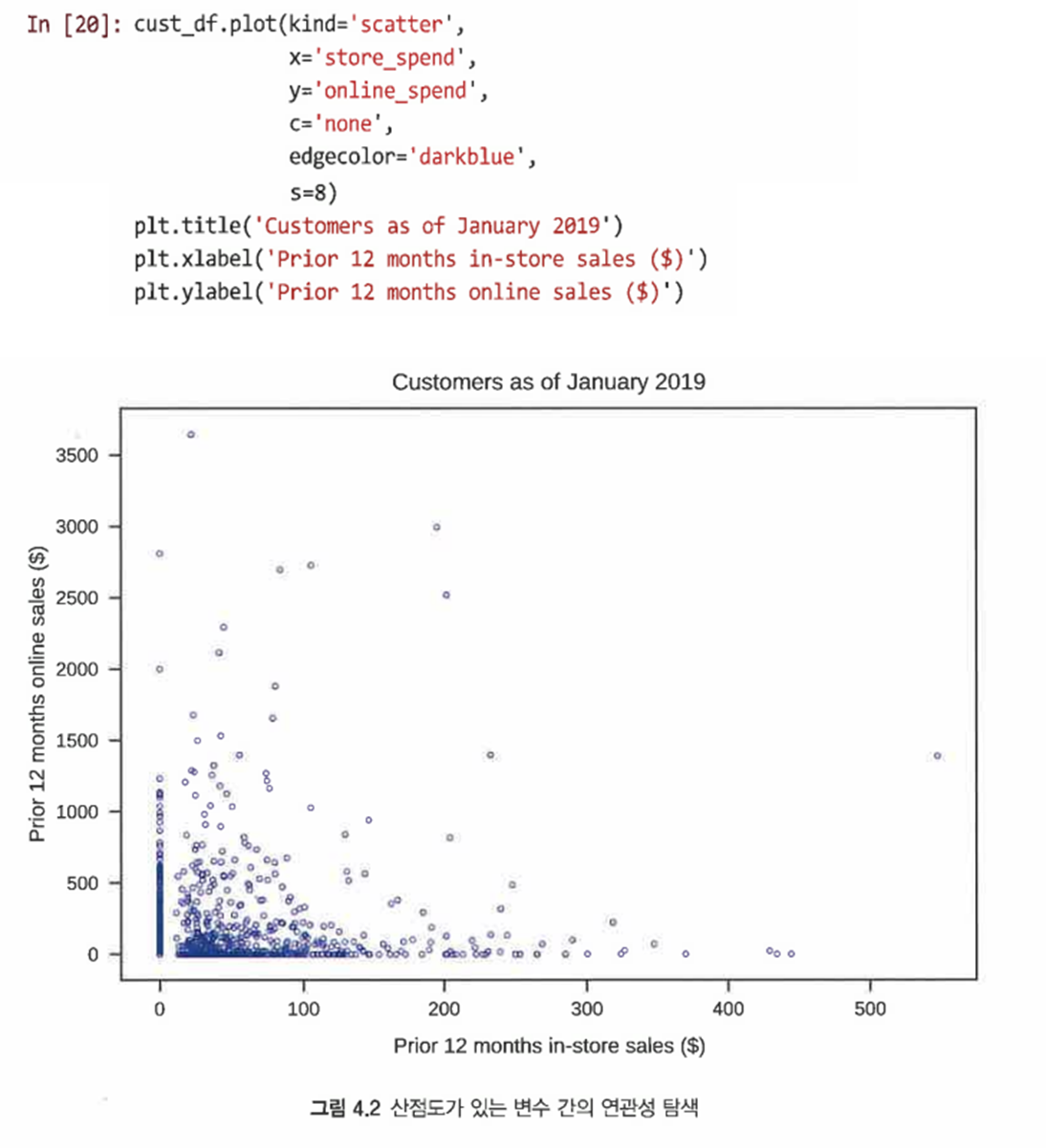
-
치우친 데이터 때문에 결과가 잘 나오지 않았으니 매장 내 판매만 히스토그램으로 추가 조사한다
-
히스토그램을 사용하면 해당 지역의 실제 포인트 밀도를 더 잘 시각화할 수 있다
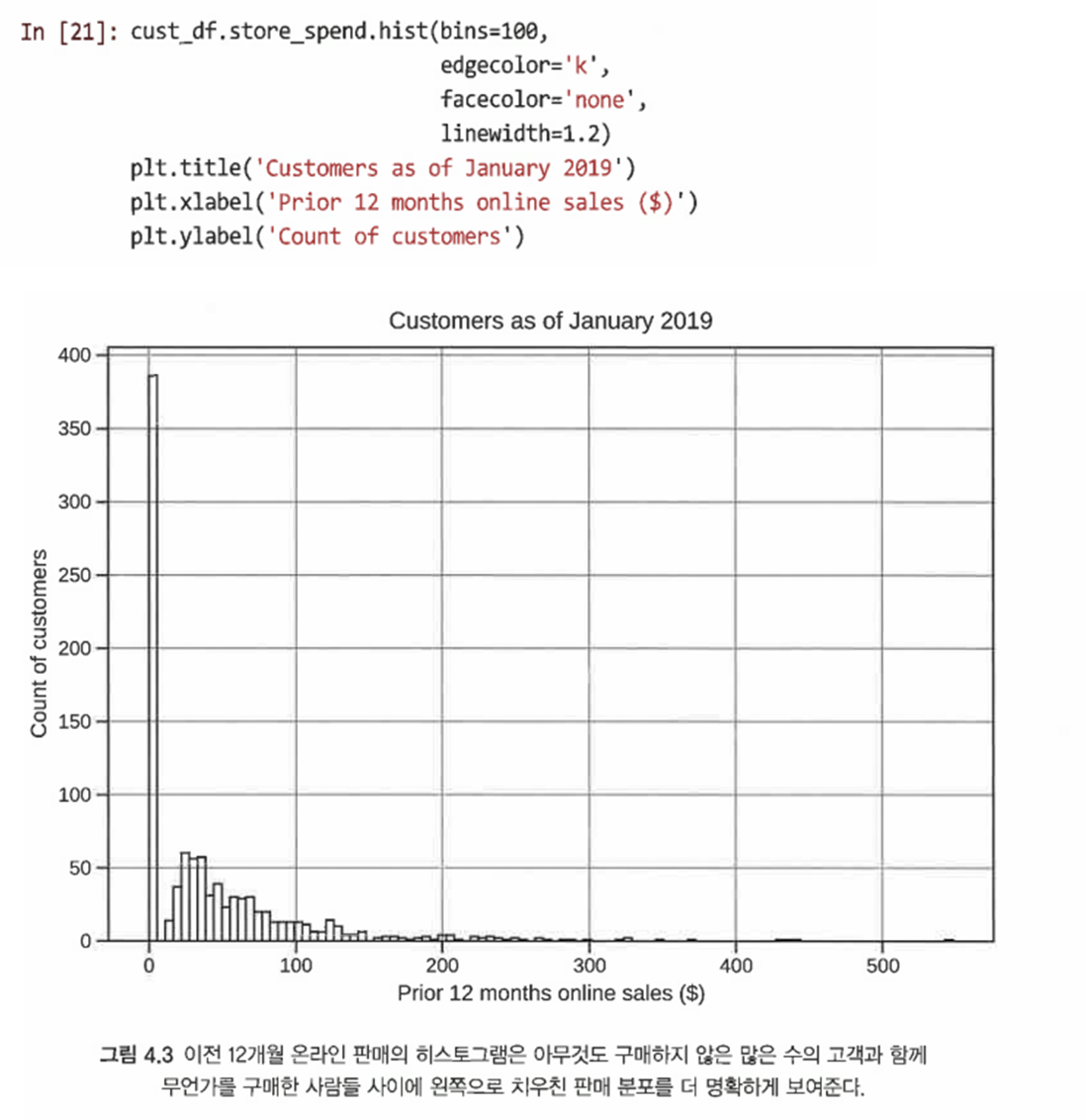
4.2.2 산점도의 포인트 색상
- 온라인 구매 성향과 오프라인 구매 성향이 이메일 활동과 관련이 있는지 여부 확인을 위해 이메일 차원 추가 생성
- groupby()를 사용해 그룹에 반복적으로 scatter() 함수를 사용해 각 하위 집합을 도식화
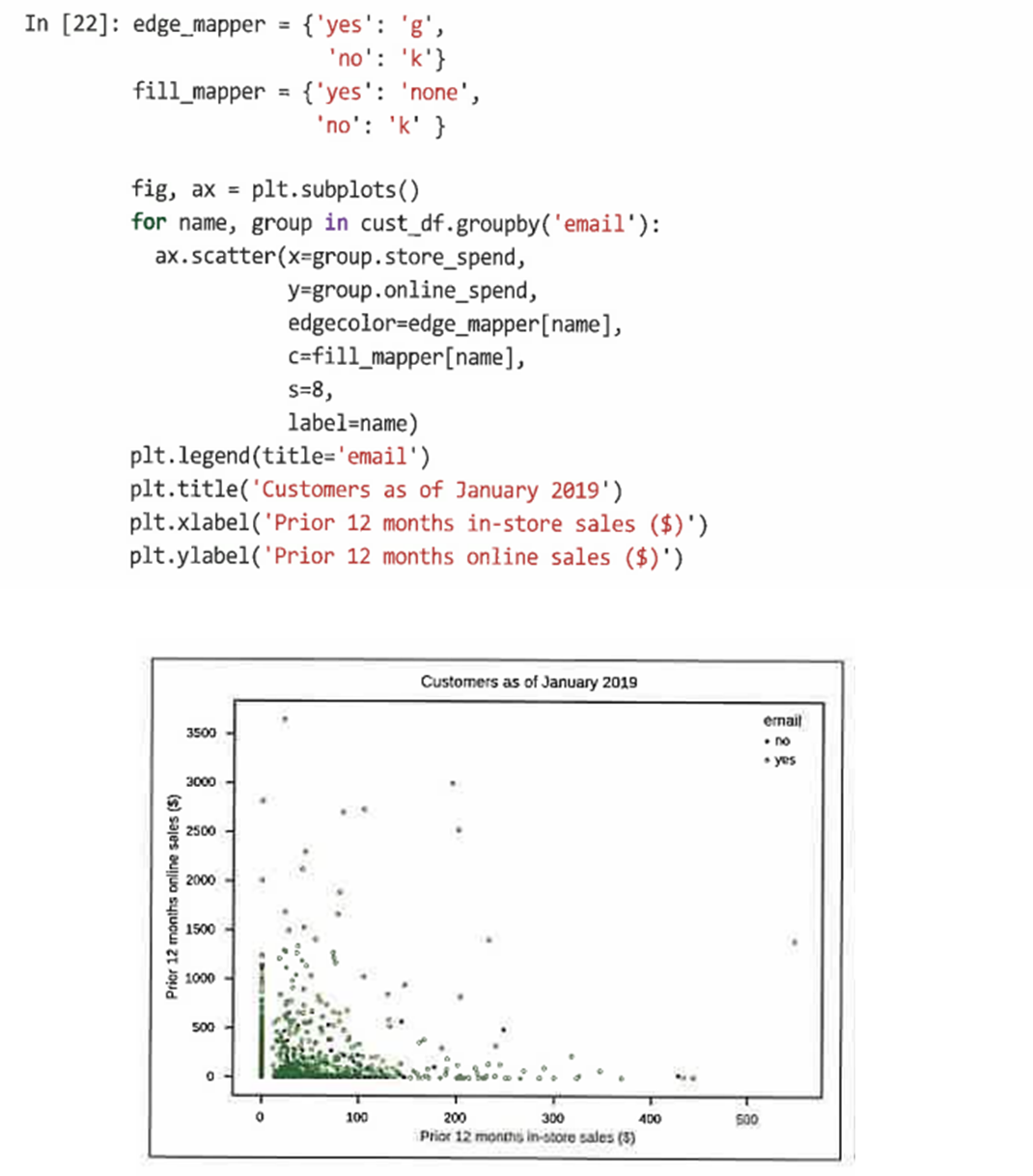
4.2.3 로그 스케일로 도식화
-
위와 같이 원시 값을 사용하면 판매 수치의 큰 왜도로 인해 결과를 확인하기가 여전히 어렵기 때문에 로그 스케일로 도식화 한다
-
plt.xscale('log')와 plt.yscale() 함수를 사용
-
이 코드에서는 log(0)이 정의되지 않았기 때문에 오류를 피하기 위해 spend+1 사용
-
cust_df의 경우 온라인 및 매장 내 판매가 모두 치우쳐 있기 때문에 두 축에 대해 로그 척도 사용
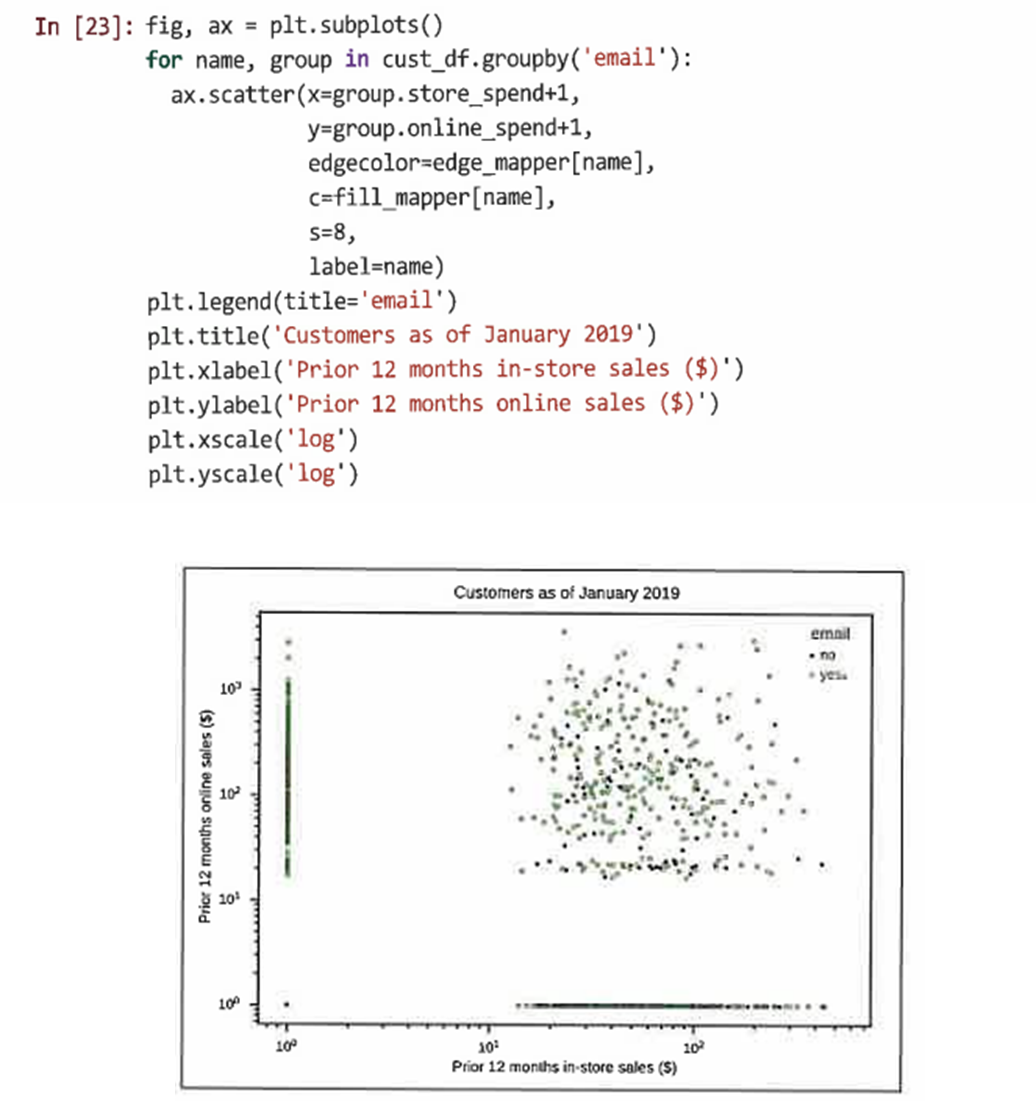
-
온라인 판매와 매장 내 판매 간에 연관성이 거의 또는 전혀 없는 것을 확인할 수 있다
-
두 채널에서 구매한 고객의 산점도에는 패턴이 표시되지 않기 때문에 온라인 판매가 매장 판매를 잠식했다는 증거가 없다
-
이메일 주소가 없는 고객이 있는 고객보다 온라인 판매가 약간 낮은 것으로 보아 고객에게 이메일 프로모션을 보낸 경우 프로모션이 효과가 있음을 추측할 수 있다
4.3 단일 그래픽 객체에서 도면 결합
- subplot() 함수를 사용해 매장과 가까운 곳에 사는 고객이 매장에서 더 많이 지출하는지, 더 멀리 사는 고객이 온라인에서 더 많이 지출하는지 여부를 살펴볼 수 있다
- sublot(221) = subplot(2,2,1)
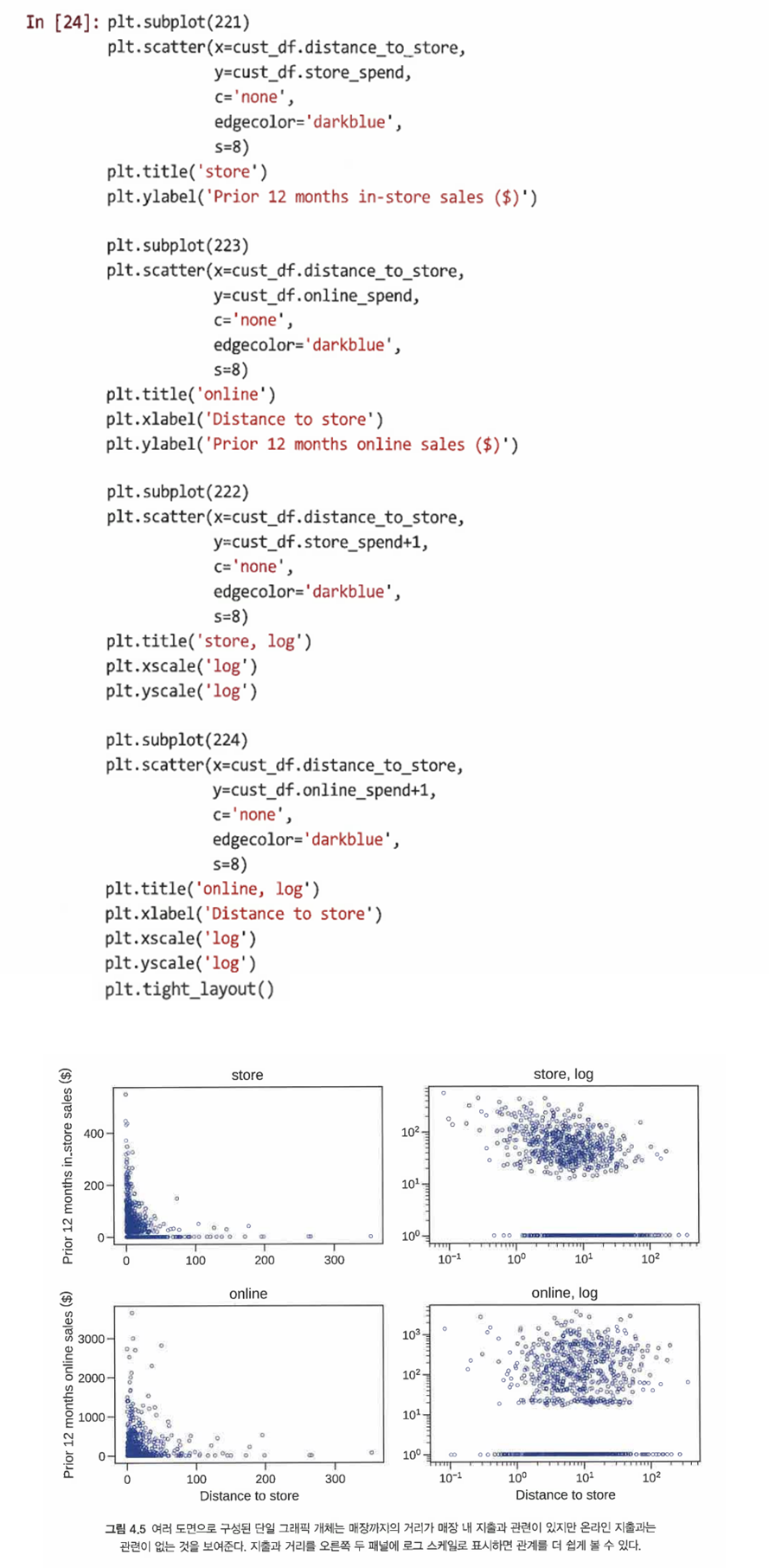
- 오른쪽 상단 패널에서 고객과 가장 가까운 매장까지의 거리와 매장 내 지출 간에 음의 관계가 있음을 알 수 있다 (가게가 가까울수록 매장 내 지출 상승)
- 반면 오른쪽 하단 패널에서 거리와 온라인 지출 사이에는 명확한 관계가 없음을 알 수 있다
4.4 산점도 행렬
4.4.1 scatter_matrix()
- pandas.plotting.scatter_matrix(dataframe)을 사용해 모든 변수 조합에 대한 별도의 산점도 생성
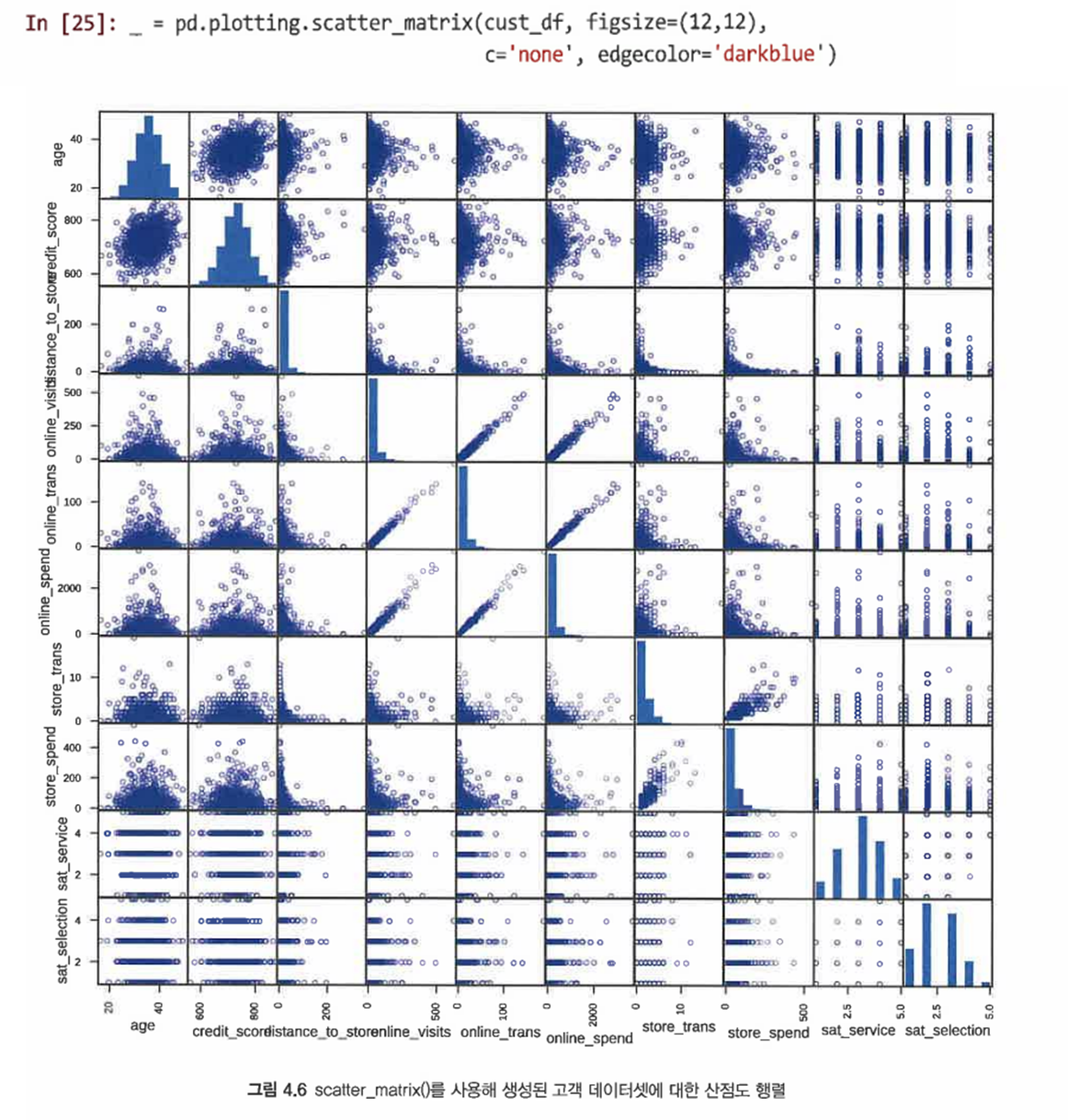
4.4.2 PairGrid()
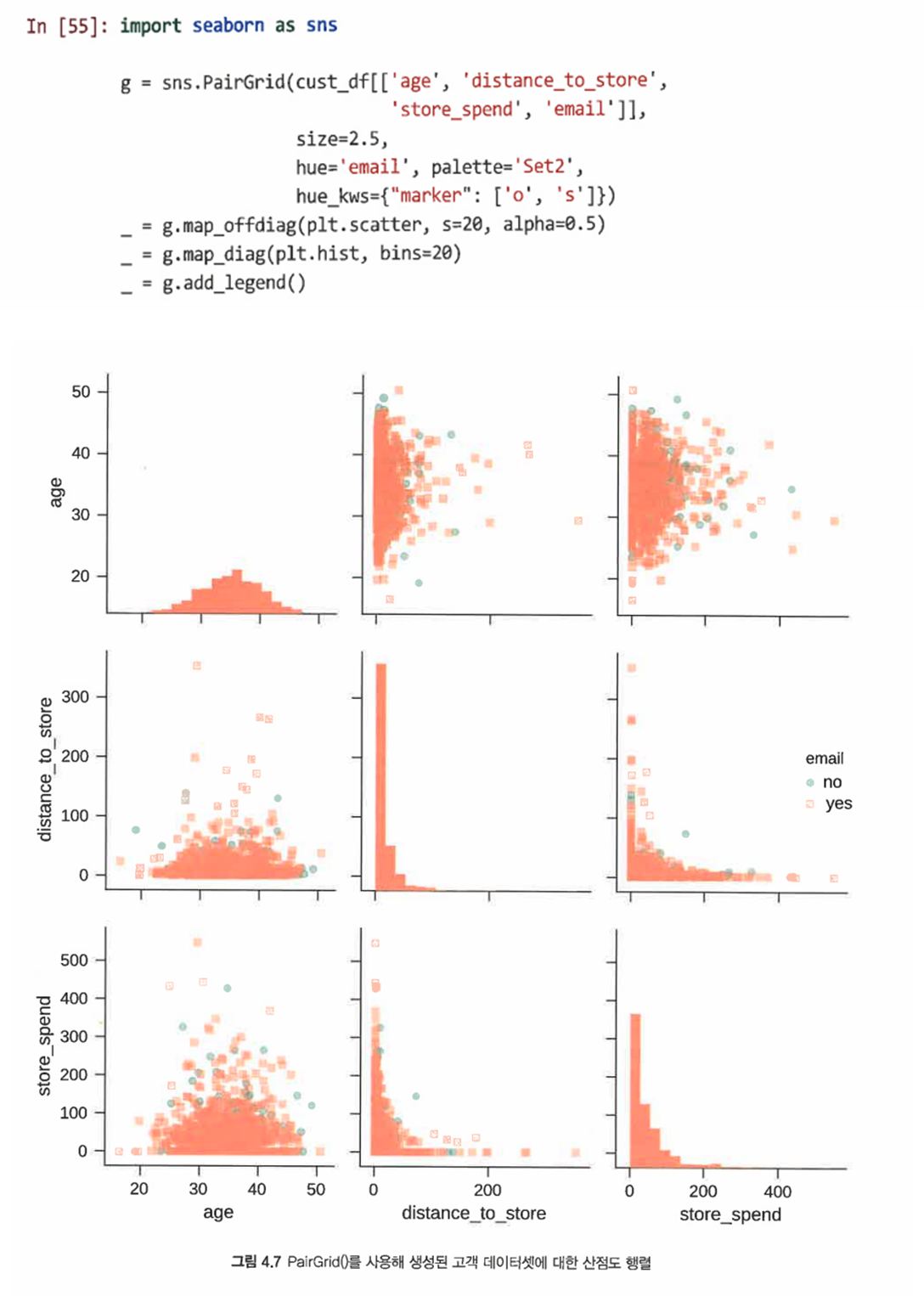
- 범주형 변수에 마커 색상 지정 가능
- PairGrid() 객체를 생성해 데이터프레임을 전달
- size 인수를 사용해 각 패널의 크기를 지정하고 이메일 열의 값을 반영하기 위한 도식화된 원소의 색조 설정
- 원을 나타내는 'o', 정방을 나타내는 's'로 마커 지정
4.5 상관 계수
-
numpy.cov() 함수를 사용해 두 변수에 대해 공분산을 계산할 수 있다
-
척도가 관련된 변수에 따라 달라지기 때문에 공분산의 크기를 해석하기 어렵다는 한계가 있다

-
피어슨의 r은 [-1, +1] 범위에 속하는 연속 측도
-
r은 두 변수가 밀접한 선형 연관성을 갖는지 여부를 평가하기 위해 쉽게 해석되는 측도가 된다
-
numpy.corrcoef() 함수를 사용

-
코헨의 경험법칙에 따라 r=0.1은 작거나 약한 연관성, r=0.3은 중간, r=0.5이상은 크거나 강한 연관성으로 간주할 수 있다
-
이러한 해석은 변수가 정규 분포를 따른다는 가정하에 이루어지기 때문에 왜곡되거나 비정규 분포는 정규 분포로 변환하고 해석해야 한다
4.5.1 상관관계 검정
- scipy.stats.pearsonr() 함수를 사용해 통계적으로 유의미한지 확인할 수 있다

- 결과가 r=0.29이고 95% 수준에서 양측 p값이 0에 매우 가깝다는 것을 알 수 있다 (귀무가설 기각)
4.5.2 상관 행렬
-
2개 이상 변수의 경우 corr() 메서드를 사용해 모든 쌍 x, y간의 상관관계를 한 번에 상관 행렬로 계산할 수 있다
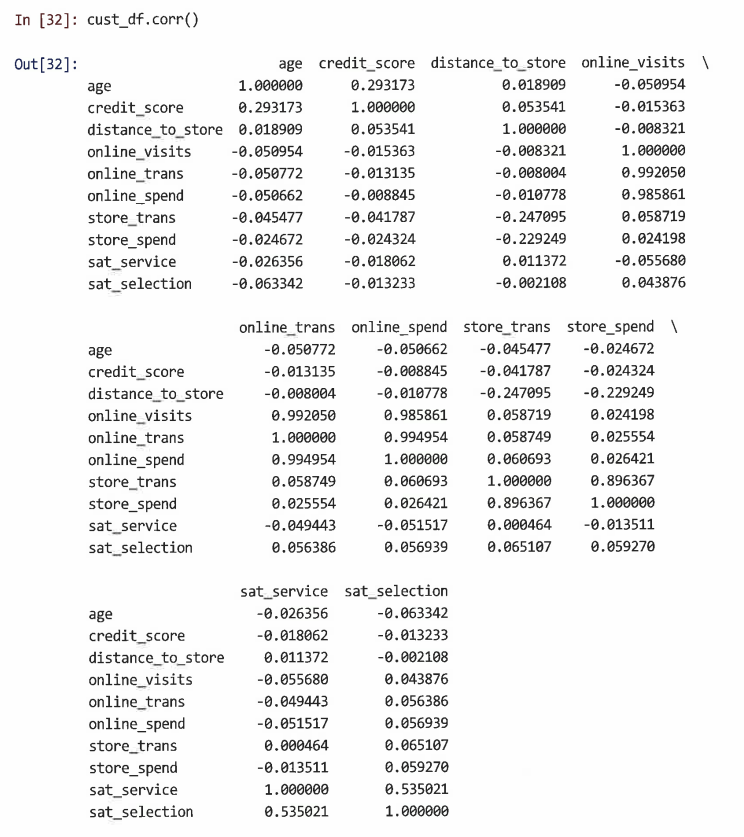
-
숫자 행렬을 스캔하는 대신 상관 행렬을 plt.imshow()에 전달해 상관관계를 시각화할 수 있다
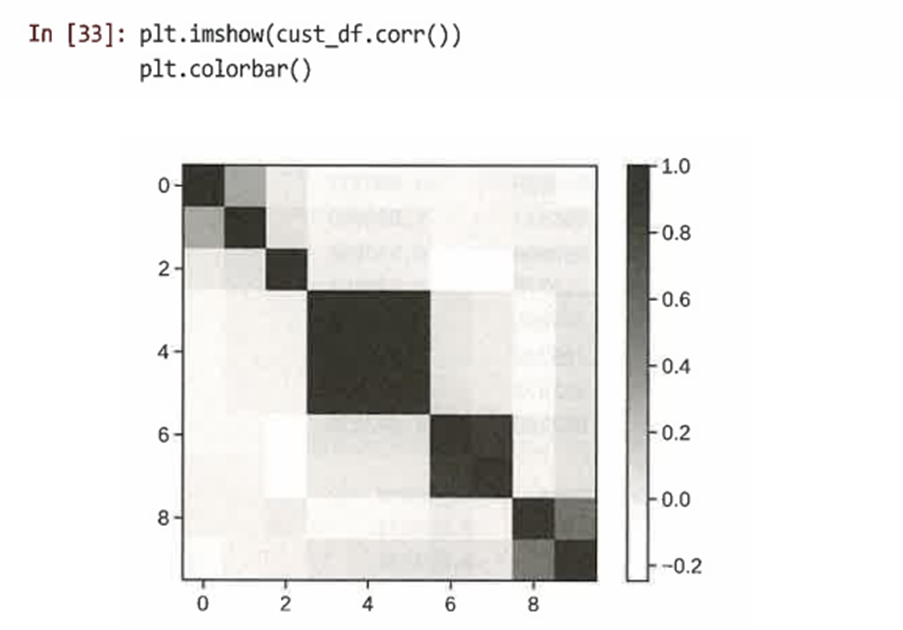
-
더 쉽게 해석할 수 있도록 heatmap()의 출력을 사용자 정의할 수도 있다
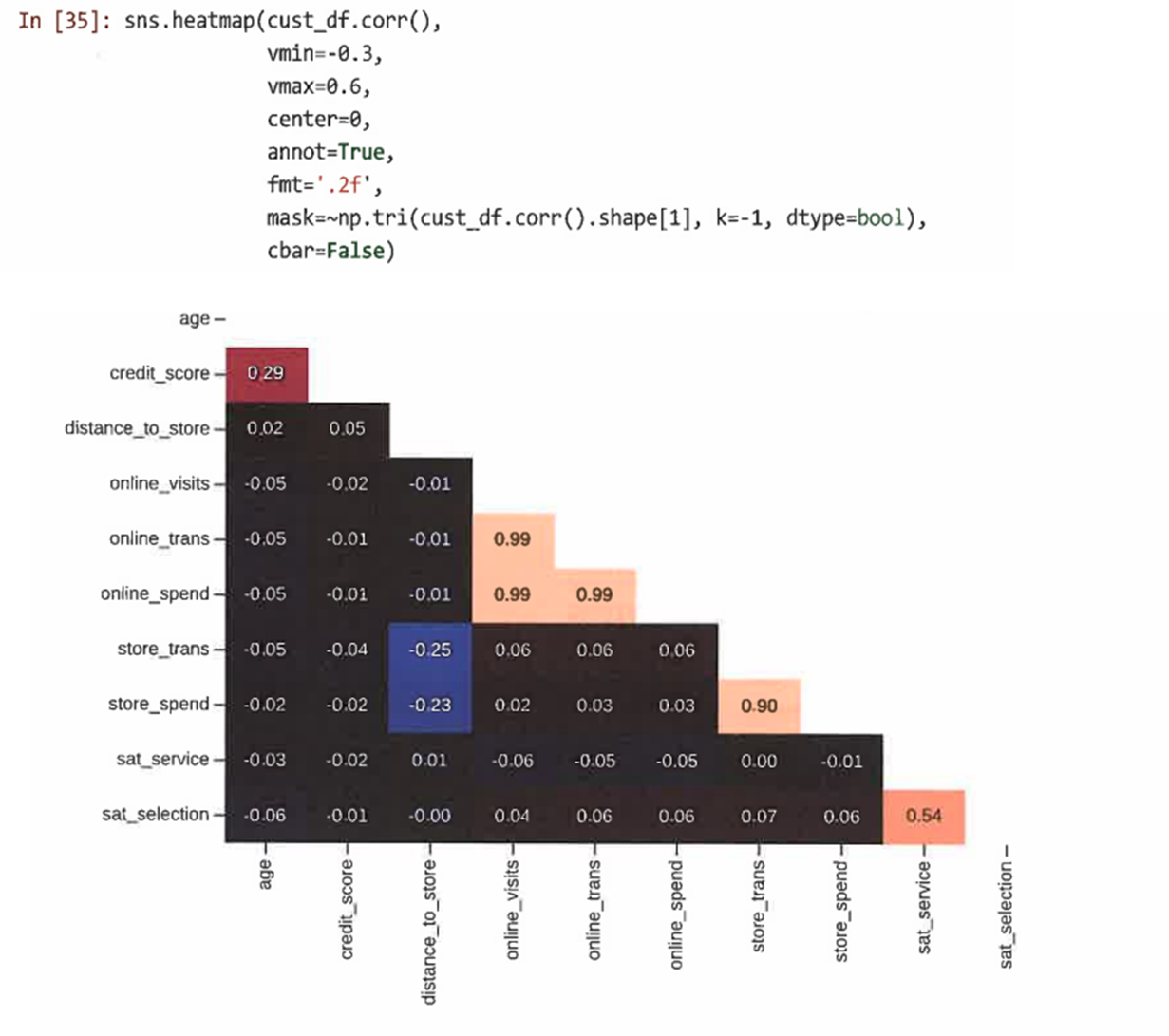
4.5.3 상관관계를 계산하기 전에 변수 변환
- 상관 계수 r은 두 변수 간의 선형 연관성을 측정하기 때문에 비선형 데이터를 선형관계로 변환할 필요가 있다
- 역제곱근은 효과적인 선형 연관성을 나타낸다

4.5.4 일반적인 마케팅 데이터 변환
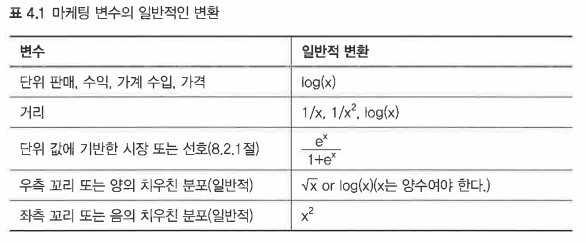
4.5.5 박스-콕스 변환
-
scipy.stats.boxcox() 함수를 이용해 람다 값을 시도해 분포가 정규 분포에 가장 잘 맞는 변환을 확인할 수 있다

-
이는 거리를 정규 분포와 최대한 비슷하게 만들기 위한 람다 값이 0.01844라는 것을 알려준다
-
dts_bc 변수에 저장된 변환 데이터가 반환된다
-
이미 정규 분포에 가까운 변수를 변환하려고 하면 boxcox()는 1에 가까운 람다 값을 찾는다

4.6 설문 응답에서 연관성 탐색
- 만족도 변수 간 연관성 파악
- 소매 업체의 서비스에 대한 만족도와 소매 업체의 제품 선택에 대한 만족도 비교
4.6.1 지터: 서수 도면을 더 유익하게 만들기
- 각 변수를 조금 흔들어 각 응답에 소량의 랜덤 노이즈를 추가한다
- np.random.normal() 사용
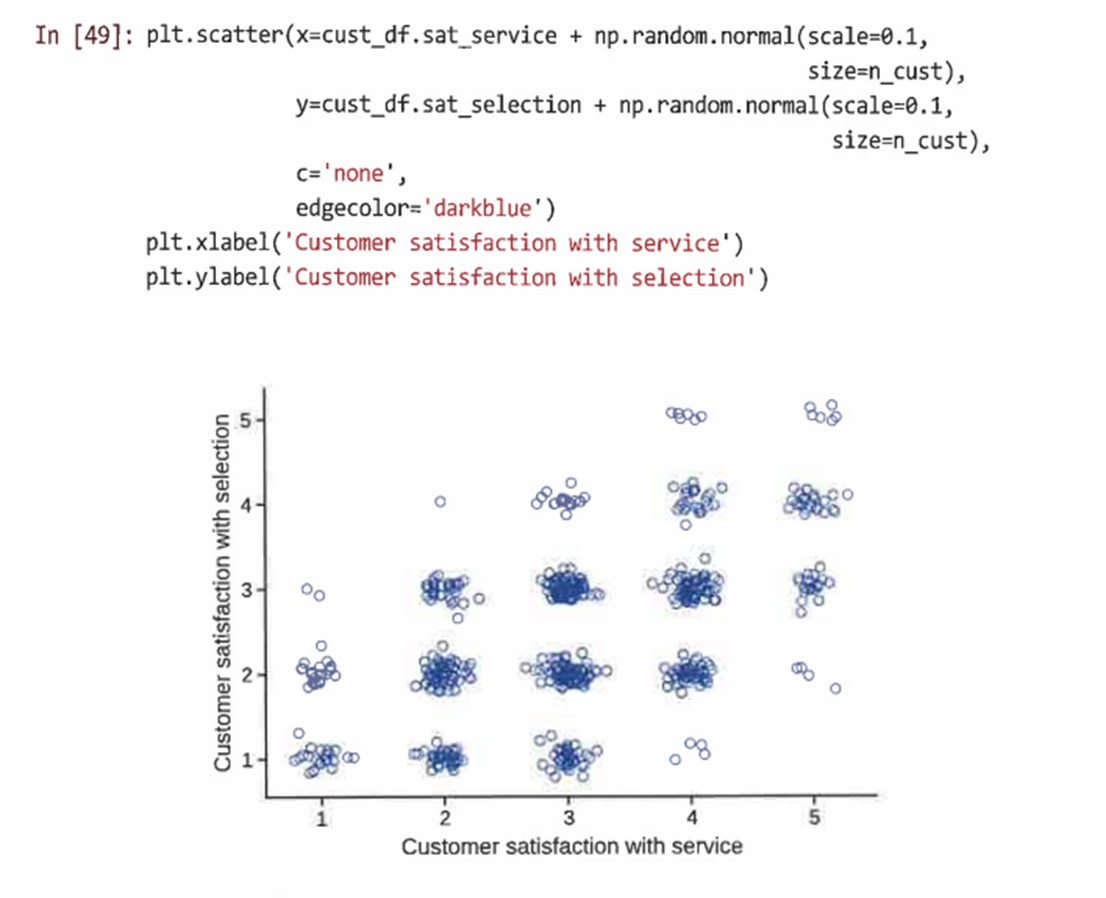
4.7 요점
