데이터 설명
3.1 데이터 시뮬레이션
3.1.1 데이터 저장: 구조 설정
-
상점 수와 각 상점에 대한 데이터 주 수 설정

-
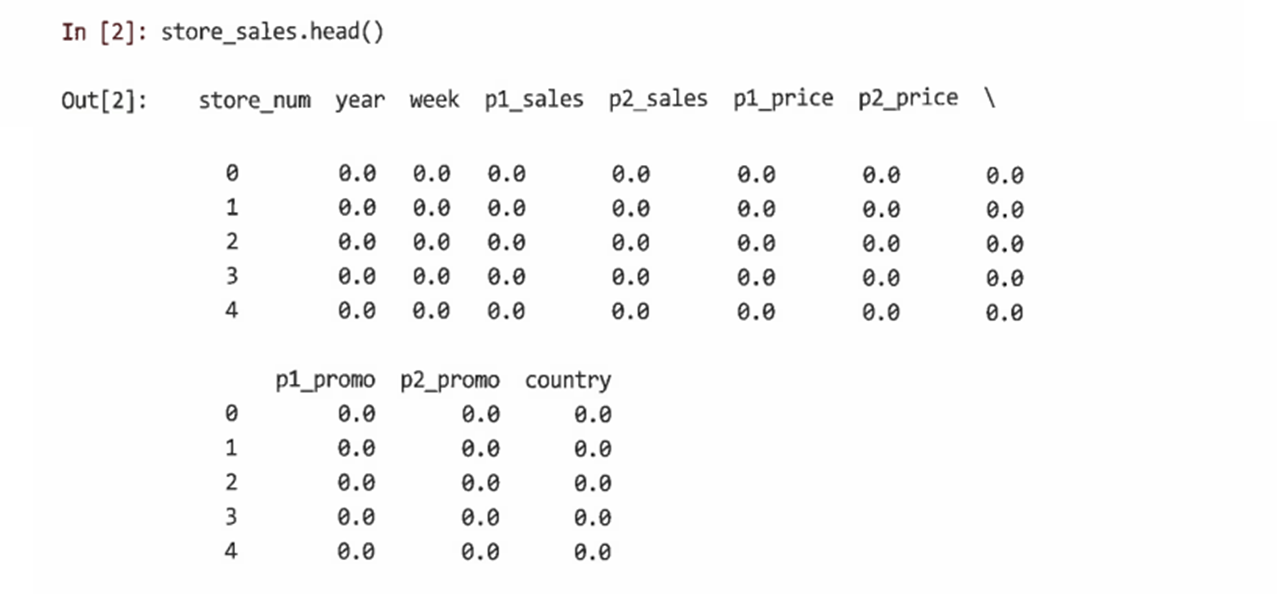
head()를 사용해 store_sales를 확인
-
설정한대로 모든 값을 0으로 설정되어 있음
-
각 상점을 식별하기 위해 store_numbers 작성
-
range를 사용해 101~120까지의 상점번호 생성
-
range 객체 출력을 위해 list로 변환

-
상점번호에서 해당 상점의 국가로 매핑되는 딕셔너리 생성
-
zip()를 사용하여 상점번호를 국가목록과 결합
-
store_country 매핑을 만들기 위해 zip 객체를 dict에 전달

-
store_sales 데이터프레임 채우기
-
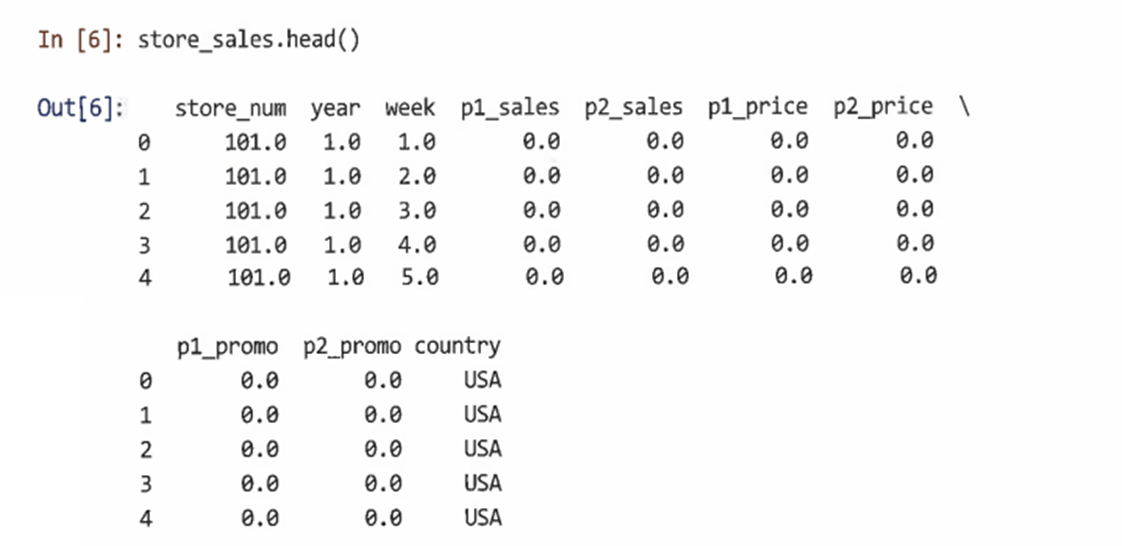
모든 매장을 각 연도와 각 주별로 살펴보고 매장 번호, 연도, 주, 국가 값 설정

-
head()로 전체 데이터 구조 확인
-
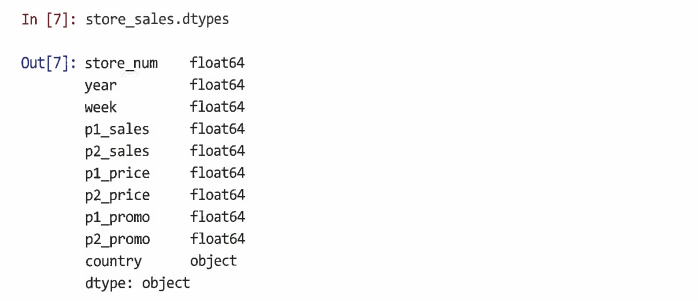
dtypes 속성으로 각 열의 유형 확인
-
그러나 국가 레이블은 실제로는 임의의 텍스트가 아닌 이산값(discrete value)이다
-
마찬가지로 store_num은 숫자가 아닌 레이블이다
-
이러한 변수를 범주형으로 재정의할 필요가 있다
-
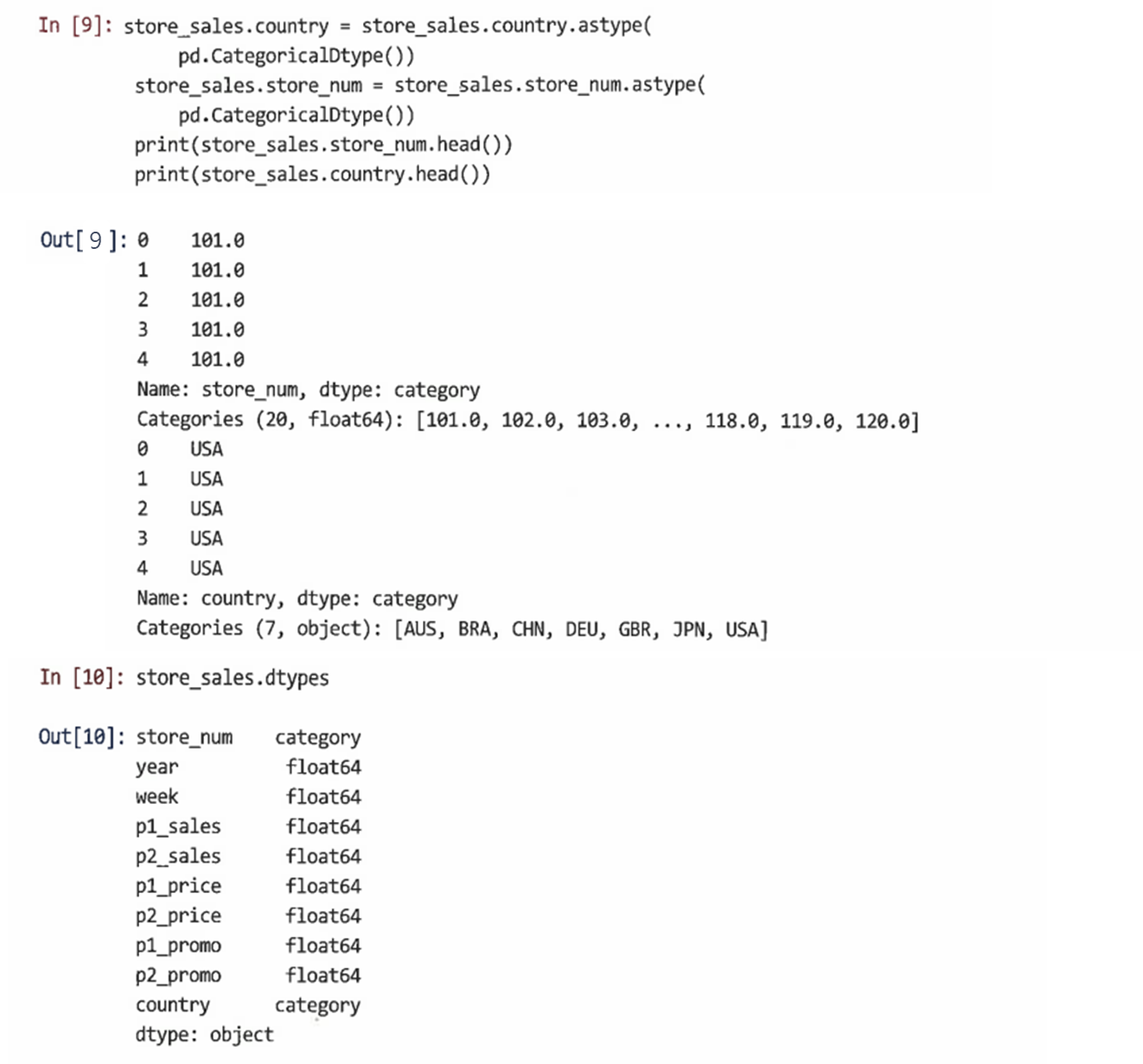
astype() 메서드를 이용해 store_sales.store_num과 store_sales.country를 범주형으로 재정의한다
-
store_num 및 country는 이제 각각 20과 7 레벨의 범주로 정의된다
-
실수 방지를 위해 첫 번째 행과 마지막 행의 데이터프레임을 검사하는 것이 좋다
-
head()와 tail() 사용해 데이터프레임의 시작과 끝을 검사하고 sample()을 사용해 임의의 샘플을 검사

3.1.2 데이터 저장: 데이터 포인트 시뮬레이션
-
임의 데이터를 시뮬레이션 하기 전에 프로세스를 복제할 수 있도록 난수 생성 시드를 성정하는 것이 중요
-
시드를 설정한 후 동일한 순서로 무작위 샘플을 다시 그릴 때 정확히 동일한 난수를 얻는다
-
다음과 같이 PRNG 시드를 설정해 명령을 시행하면 동일한 결과를 얻을 수 있다

-
매주 각 매장에 대해 각 제품이 홍보됐는지 여부를 무작위로 결정하기 위해 np.random.binomial(n, p, size) 함수를 사용해 이항 분포에서 추출
-
제품 1에 10%, 제품 2에 15%의 판촉 가능성 확률을 무작위로 할당

-
제품 1에 대한 판촉 수를 보고 값이 현실적인지 확인 가능

-
데이터의 각 행에서 각 제품의 가격 설정
-
각 제품이 전체적으로 $2.19에서 $3.19에 이르는 5가지 개별 가격대 중 하나로 판매된다고 가정
-
5개의 가격 포인트로 벡터를 정의하고 np.random.choice(a, size, replace)를 사용해 데이터 행(size=n_rows)만큼 여러 번 매주 가격을 무작위로 추출
-
5개의 가격은 여러 번 샘플링되므로 복원을 동반한 추출이다(replace=True)
-
이때, 고유한 값이 몇 개만 있는 경우라도 가격은 범주형 요인이 아닌 숫자이다 (가격에는 산술이 수행되기 때문)

-
마지막 단계로 매주 판매 수치를 시뮬레이션한다
-
여기서는 판매를 2개의 제품과 각 제품의 판촉 상태에 대한 상대 가격의 함수로 계산한다
-
품목 판매량은 단위수로 계산되므로 푸아송 분포 np.random.poisson(lam, size)를 사용해 개수 데이터를 생성한다
-
size: 추출 개수, lam: 푸아송 분포를 정의하는 매개변수인 람다(주당 단위의 예상 또는 평균값)
-
각 행(size=n_rows)에 대해 랜덤 푸아송 개수를 추출하고 제품 1의 평균 판매량(lam)을 제품 2보다 더 높게 설정한다

-
이제 상대 가격에 따라 그 개수를 늘리거나 줄인다
-
가격 효과는 선형보다는 종종 로그 함수를 따르기 때문에 np.log(price)를 사용
-
여기서는 판매가 가격에 반비례할 것으로 가정

-
마지막으로 각 제품이 매장에서 홍보될 때 매출이 30~40% 증가한다고 가정
-
판촉 상태 벡터에 각각 0.3 또는 0.4를 곱한 다음 판매 벡터에 이를 곱한다
-
floor() 함수를 사용해 분수값을 삭제하고 주간 단위 판매에 대한 정수 개수를 확인한 다음 해당 값을 데이터프레임에 넣는다
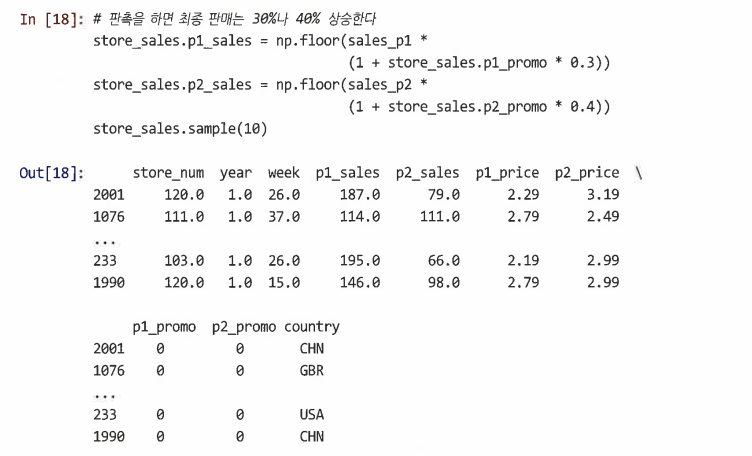
3.2 변수를 요약하는 함수
3.2.1 언어 요약: groupby()
-
groupby()는 pandas 데이터프레임의 메서드
-
by 인수는 그룹화할 열을 지정
-
SeriesGroupBy 객체를 반환, 변수에 저장하거나 직접 처리 가능
-
해당 객체는 데이터프레임 내에 서로 다른 열을 포함하며 점 표기법을 통해 접근 가능
-
mean(), sum() 등과 같은 pandas 분석 방법을 해당 그룹에 적용할 수 있다

-
요인 리스트를 사용해 둘 이상의 요인으로 그룹화할 수 있다
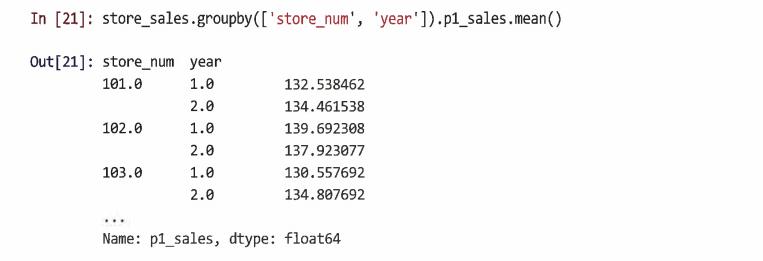
-
groupby()의 한계: 결과가 항상 읽기 쉬운 것이 아니며, 재사용을 위해 구조화되지 않는다
-
단일 수준 그룹화: pandas.DataFrame() 함수를 사용해 출력을 데이터프레임으로 변경 가능
-
다단계 그룹화: unstack() 메서드를 사용해 인덱스를 피벗(pivot)하고 데이터프레임 반환

-
또는 sum()을 통해서 국가별 P1의 총 판매량을 계산하는 방식으로도 그룹화할 수 있다
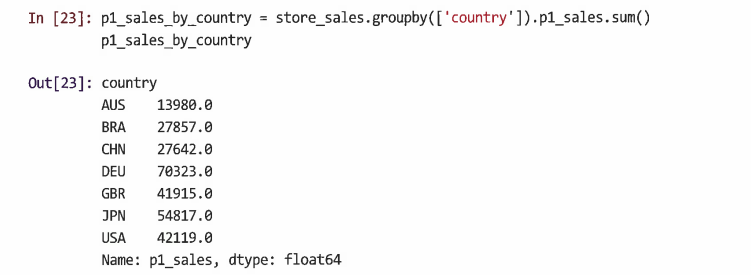
3.2.2 이산 변수
-
이산 데이터를 설명하는 기본 방법: 빈도수
-
value_counts() 메서드를 사용해 변수에서 발생하는 각 값이 관찰된 횟수 계산
-
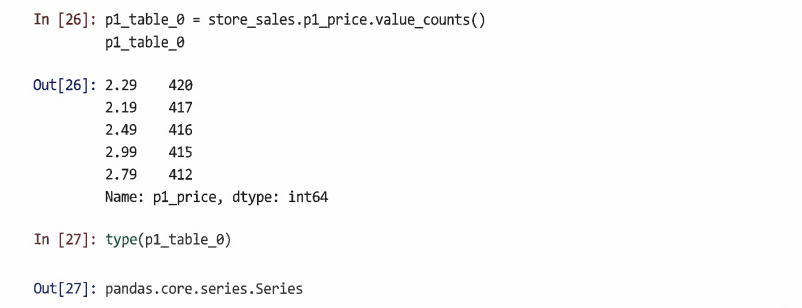
store_sales에서 제품 1이 각 가격대에서 판매된 횟수를 확인할 수 있다
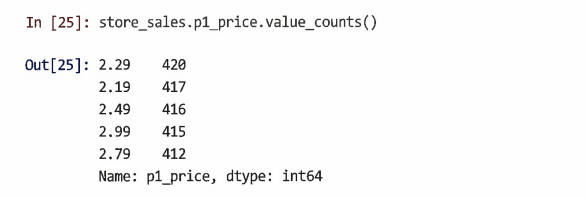
-
value_counts()는 기본적으로 내림차순 정렬
-
정렬을 하고 싶지 않다면 sort=False 사용
-
개수가 아닌 비율을 반환하고 싶다면 normalize=True 사용
-
value_counts()에 의해 생성된 테이블을 저장하려면 이름이 지정된 객체에 동일한 명령을 할당하면 된다
-
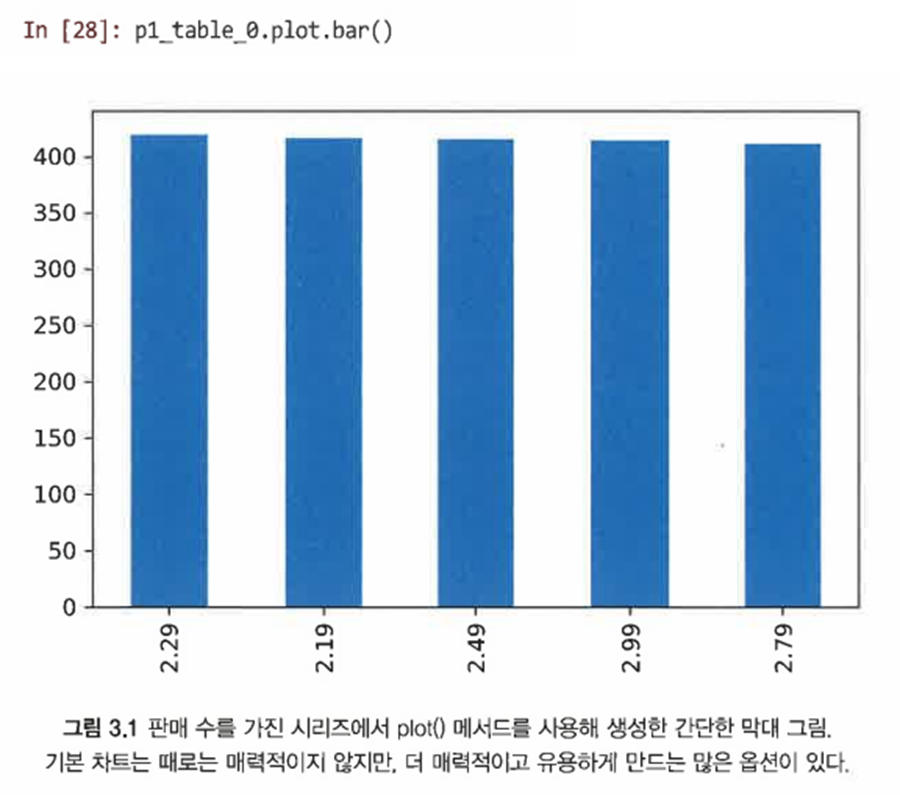
plot() 메서드를 사용해 빠르게 도면 생성 가능
-
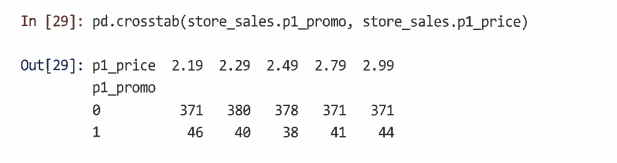
pandas.crosstab() 함수를 사용해 각 제품이 각 가격대에서 얼마나 자주 홍보되었는지 확인 가능 (양방향 교차 탭에 대해 각 수준에서 관측치 수를 생성)
-
그러나 좀 더 일반적인 접근 방식은 groupby() 메서드를 사용하는 것

-
groupby()를 사용하면 개수뿐만 아니라 산술 평균과 같은 다른 함수도 계산 가능
-
또한 데이터를 임의의 열 집합으로 그룹화 가능
-
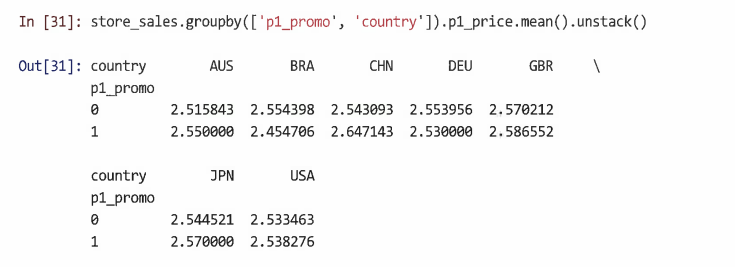
예를 들어 제품, 판촉 상태, 국가별로 평균 가격 계산 가능
-
변수에 결과를 할당한 다음 p1_table_0의 price에 있는 총판매량으로 나누면 제품 1이 각 가격 포인트에서 판촉 중인 정확한 비율을 계산할 수 있다
-
div() 메서드는 p1_table_0에 있는 일련의 카운트와 p1_table_1의 각 행 사이에 원소별 나누기를 적용한다

-
이러한 방식으로 운영 결과를 결합하면, 필요에 따라 분석을 반복할 수 있는 코드와 함께 원하는 결과를 정확하게 생성할 수 있다
3.2.3 연속 변수
-
연속 데이터의 경우 분포 측면에서 데이터를 요약하는 것이 더 유용
-
이를 수행하는 가장 일반적인 방법이 데이터의 범위, 중심, 데이터가 집중되거나 분산되는 정도, 관심 있는 특정 지점을 설명하는 수학 함수를 사용하는 것
-
다음은 데이터프레임의 숫자 열과 같은 숫자형 벡터 데이터에 대한 통계를 계산하는 일부 pandas 함수이다
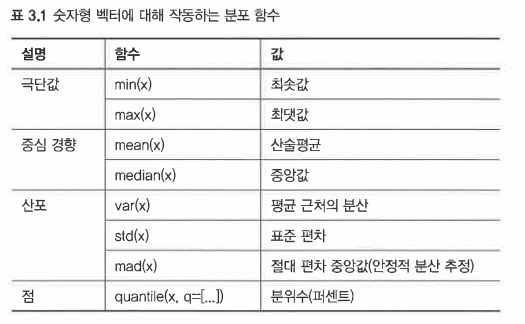

-
quantile()의 경우 q= 인수를 변경해 다른 분위수를 찾을 수 있다
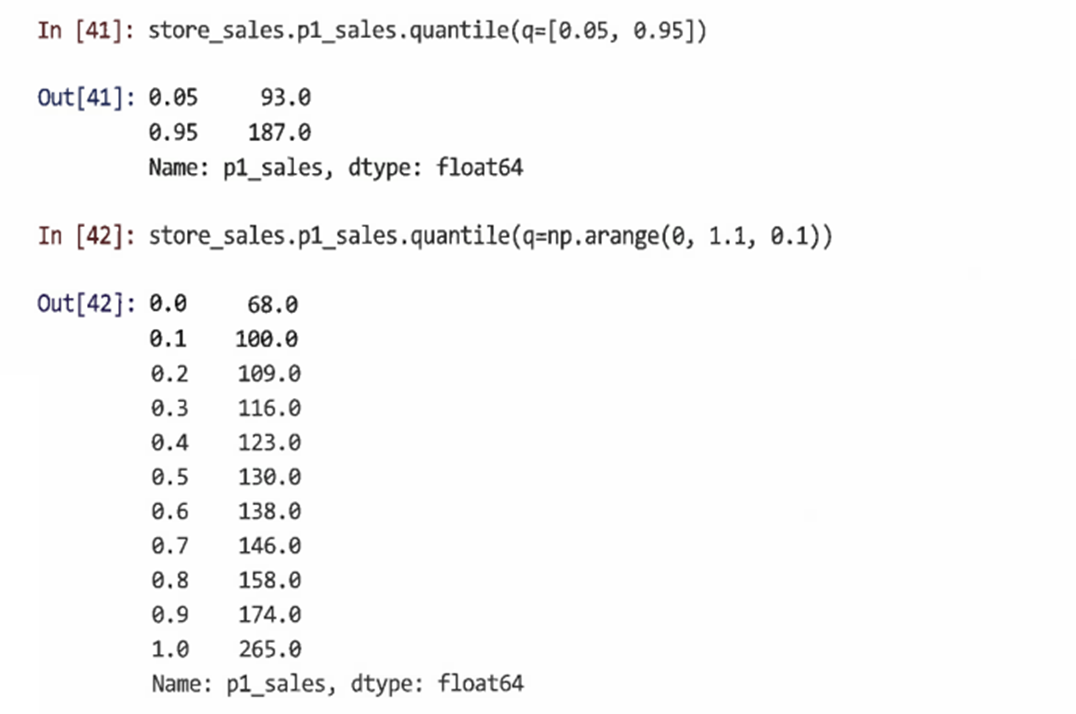
-
다음은 파이썬의 여러 위치에서 시퀀스를 사용할 수 있음을 보여준다
-
이 경우 numpy.arange(start, stop, step)을 사용해 시퀀스를 생성하고 벡터 0, 0.1, 0.2 ... 1.0을 생성함으로써 모든 열 번째 백분위수를 찾는다
-
여기서는 십진수 값을 원하기 때문에 내장 range() 함수 대신 numpy.arange()를 사용한다 (range()는 정수 값만 지원하기 때문)
-
numpy.arange()는 start 인수는 포함하지만 stop 인수는 포함하지 않기 때문에 벡터에 1.0을 포함하려면 stop 인수를 원하는 최댓값과 단계의 합이 되도록 설정해야 한다
-
단위 판매 또는 가계 소득과 같이 마케팅에서 일반적으로 발생하는 기울어진 비대칭 분포의 경우 산술mean()과 표준편차std()에 오해의 소지가 있을 수 있다
-
이 경우 median() 및 사분위수 범위(IQR)가 분포를 요약하는데 더 유용하다

-
중앙값과 사분위수 범위를 기반으로 제품 1과 제품 2의 매출 요약을 위해 데이터프레임으로 요약 통계를 조합할 수 있다

-
이 사용자 정의 요약을 통해 중앙값 판매가 제품 1에 대해 더 높고 제품 1의 판매 변동도 더 심하다는 것을 알 수 있다
-
이 코드를 통해 새 판매 데이터가 있을 때 다시 실행해 요약 통계표의 수정된 버전을 생성할 수도 있다
3.3 데이터프레임 요약
3.3.1 describe()
-describe()를 사용하면 모든 변수에 대한 몇 가지 기술 통계량이 출력된다
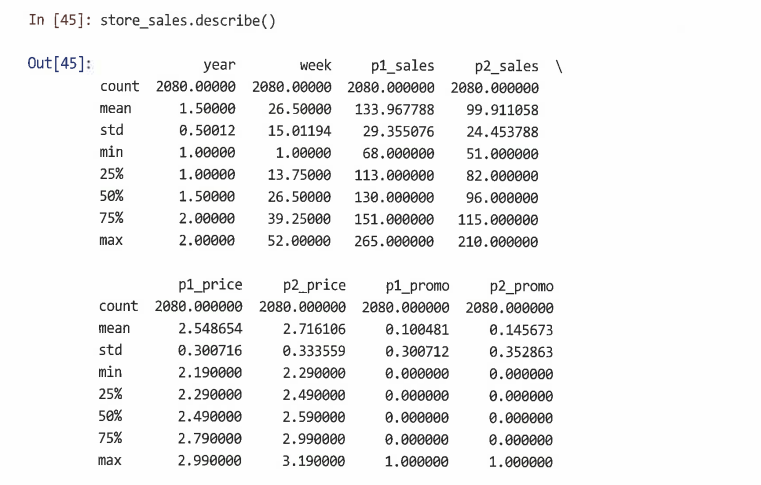
-describe()는 단일 벡터에 대해서도 유사하게 작동한다
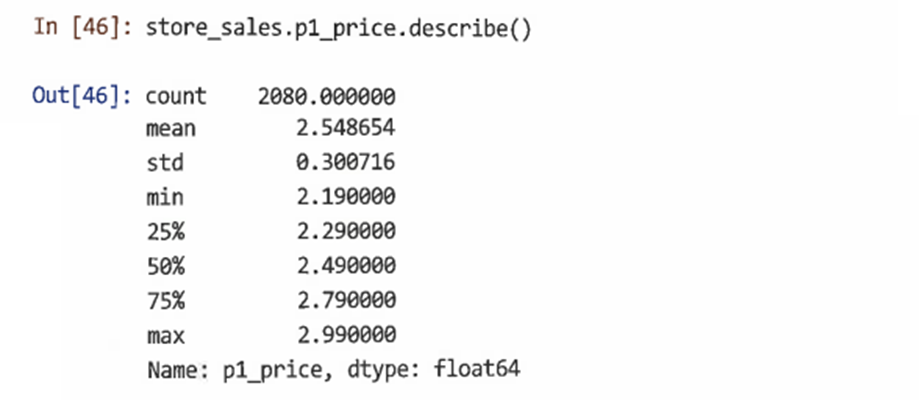
-describe()의 가장 중요한 용도는 데이터를 임포트한 후 빠른 품질 검사를 수행할 수 있는 것이다
- 이상값 또는 잘못 입력된 데이터에 대한 최솟값과 최댓값을 확인하고 평균과 중앙값(50%)가 합리적이고 서로 유사하다는 것을 확인해야 한다
3.3.2 데이터 검사에 대한 권장 접근법
- 데이터셋을 컴파일하거나 가져온 후 검사하는 일반적인 접근 방식

3.3.3 apply()*
- apply(function, axis, ...)는 데이터프레임의 각 행 및 열에 지정한 모든 함수를 실행한다
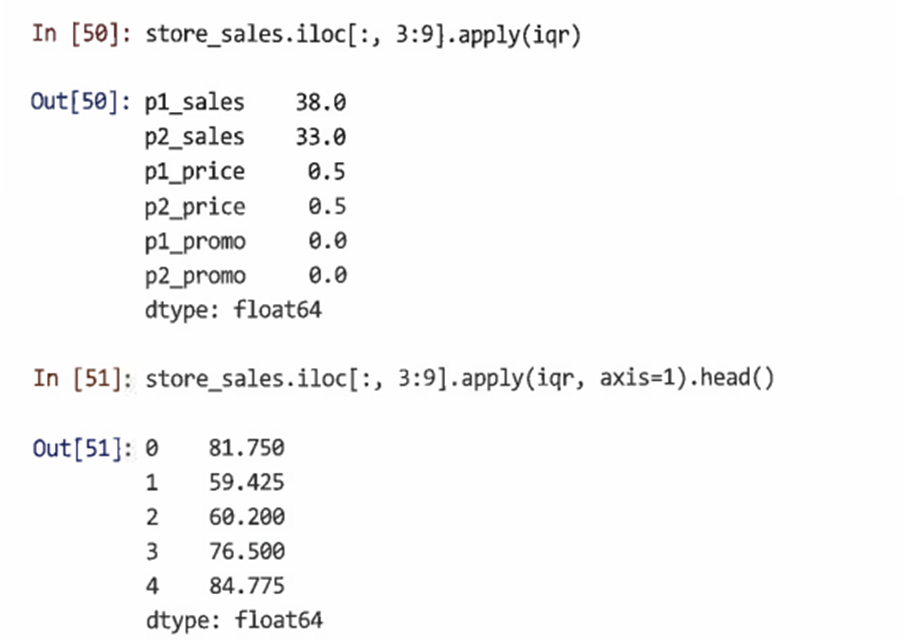
- 람다(lambda) 함수라는 임시 익명 함수를 정의하여 복수의 열에 apply() 할 수도 있다

-위와 같은 분석을 통해 p1_sales과 p2_sales의 평균이 중앙값보다 주당 약 3회 정도 더 크다는 것을 알 수 있으며, 평균을 끌어올리는 매우 높은 판매량을 가진 몇 주가 있다는 결론을 도출할 수 있다
3.4 단일 변수 시각화
3.4.1 히스토그램
-
hist() 메서드를 사용해 히스토그램 생성
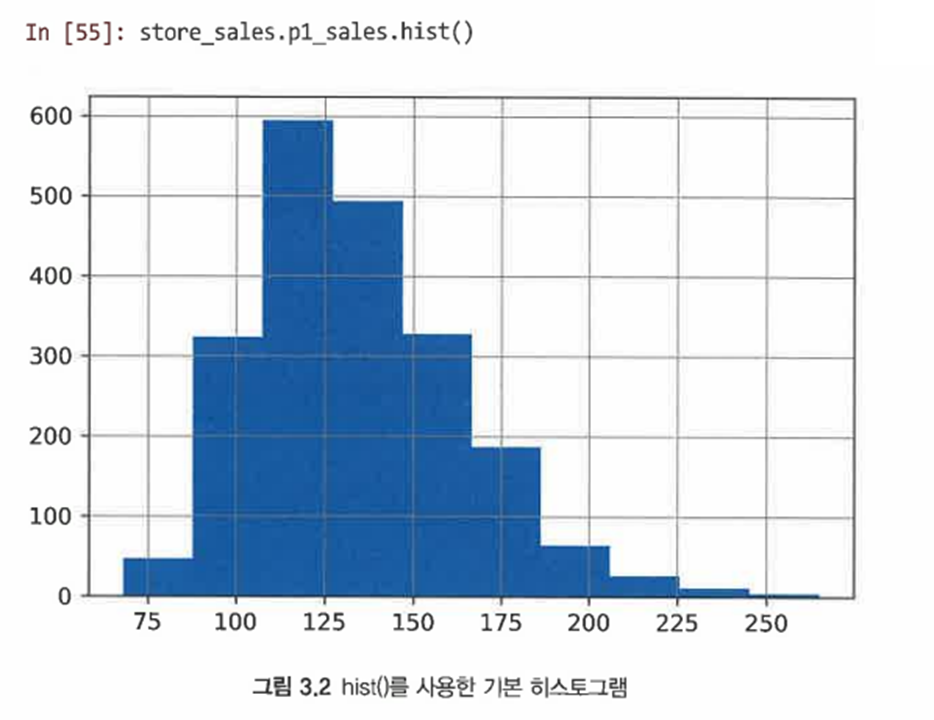
-
matplotlib.pyplot을 임포트하고 다음과 같은 함수를 사용해 제목과 축 레이블을 변경할 수 있다

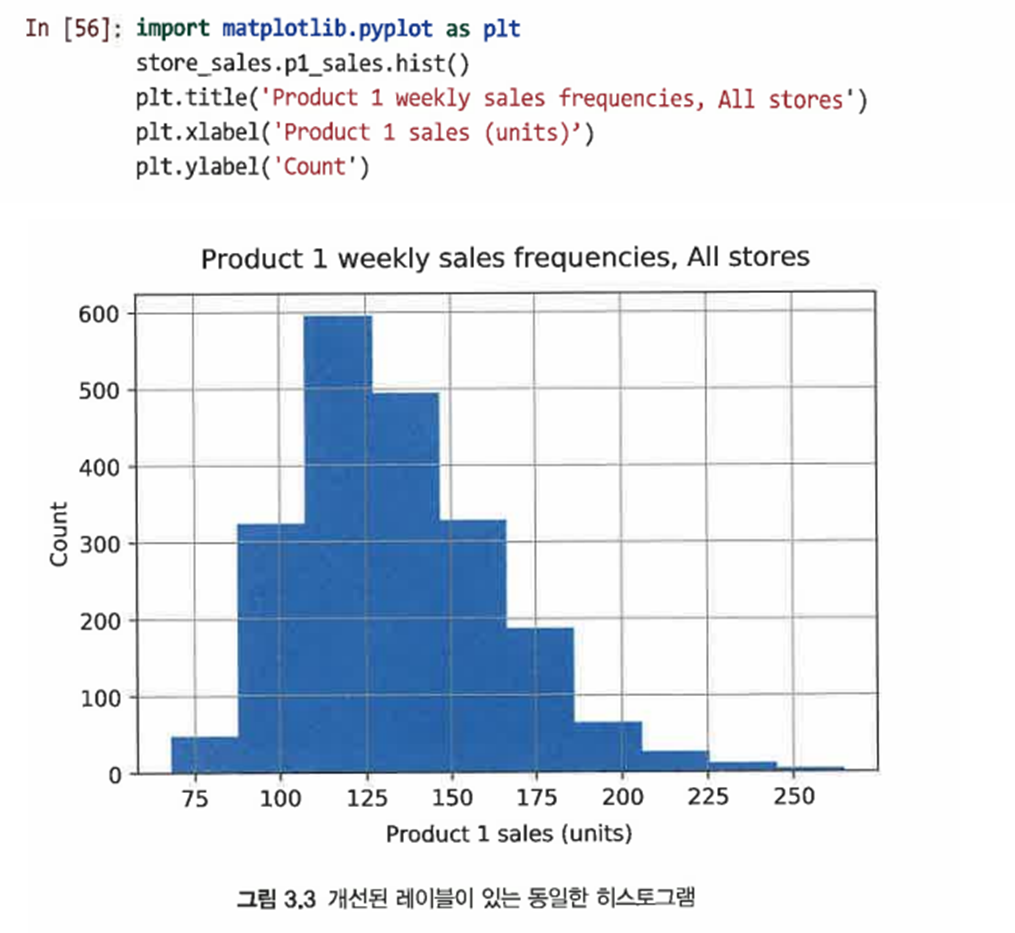
-
다음과 같은 추가 인수를 사용하여 히스토그램의 설정을 조절할 수 있다
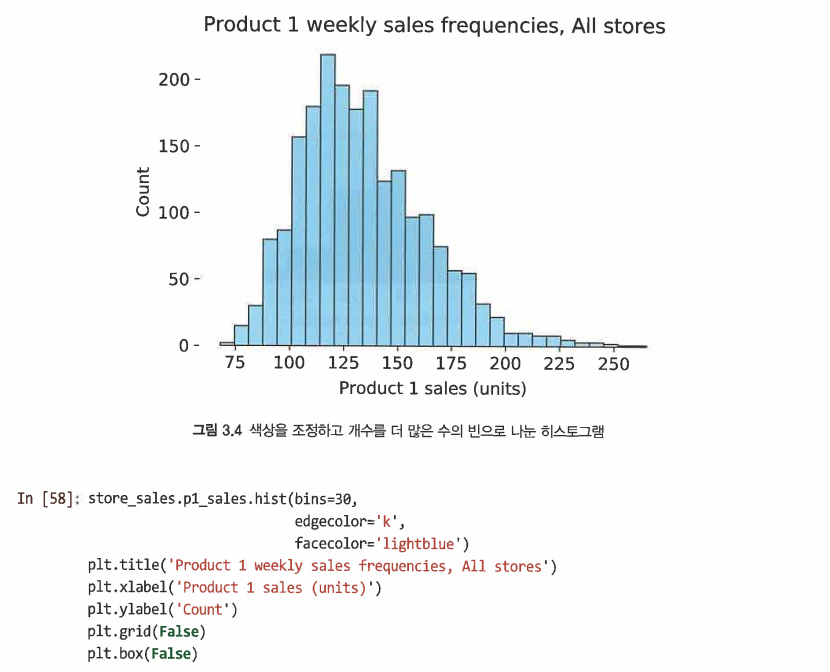
-
막대의 높이에 대한 y축의 값이 개수에 따라 변경되는 것을 방지하기 위해 개수 대신 상대 빈도를 사용해 절댓값으로 만들 수 있다 (이를 통해 서로 다른 크기의 샘플에서 y축을 비교할 수 있다): density=True
-
기본 눈금을 사용하는 대신 x축 번호를 명시적으로 지정할 수도 있다: plt.xticks()
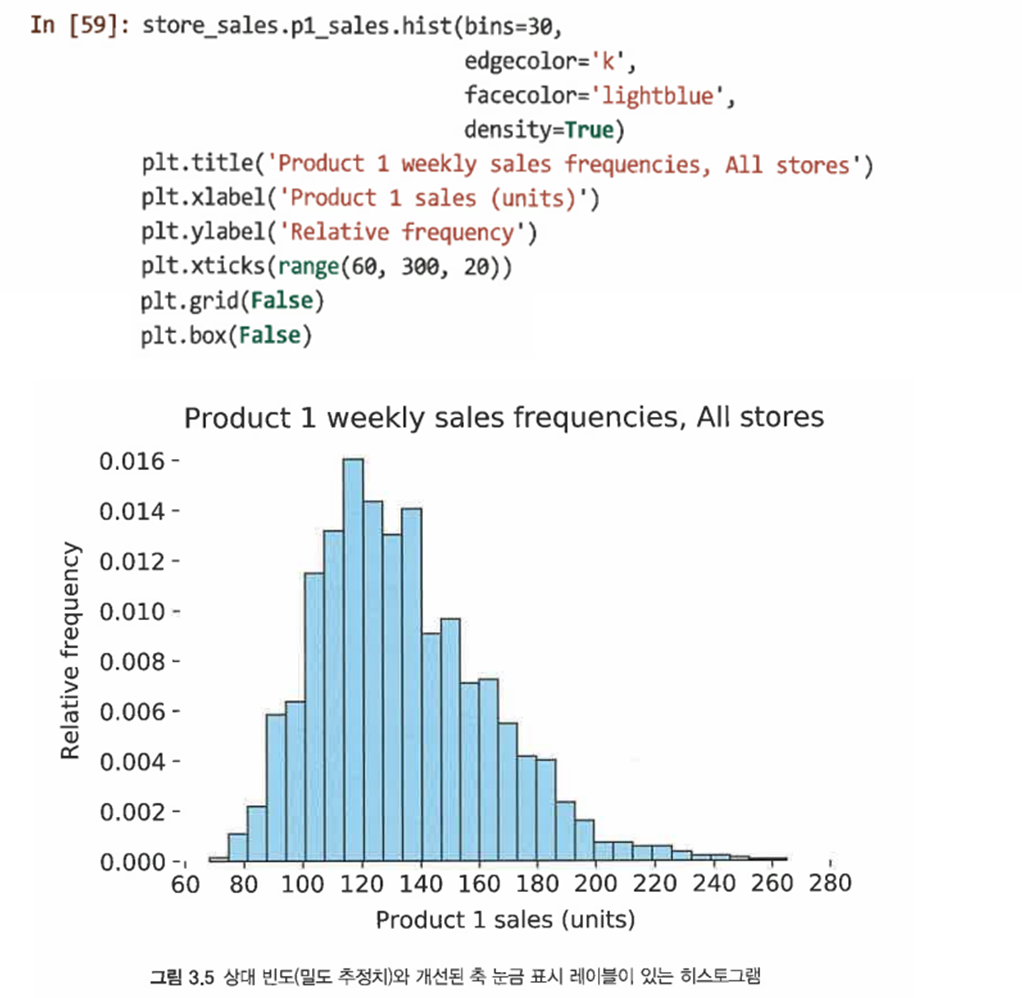
-
평활화 추정선(smoothed estimation line)을 추가한다
-
이를 위해 p1_sales 시리즈의 density() 도식화 메서드를 사용한다
-
밀도 도면은 축 자동 크기 조정을 방해하므로 plt.xlim()을 사용해 x축 범위를 지정한다
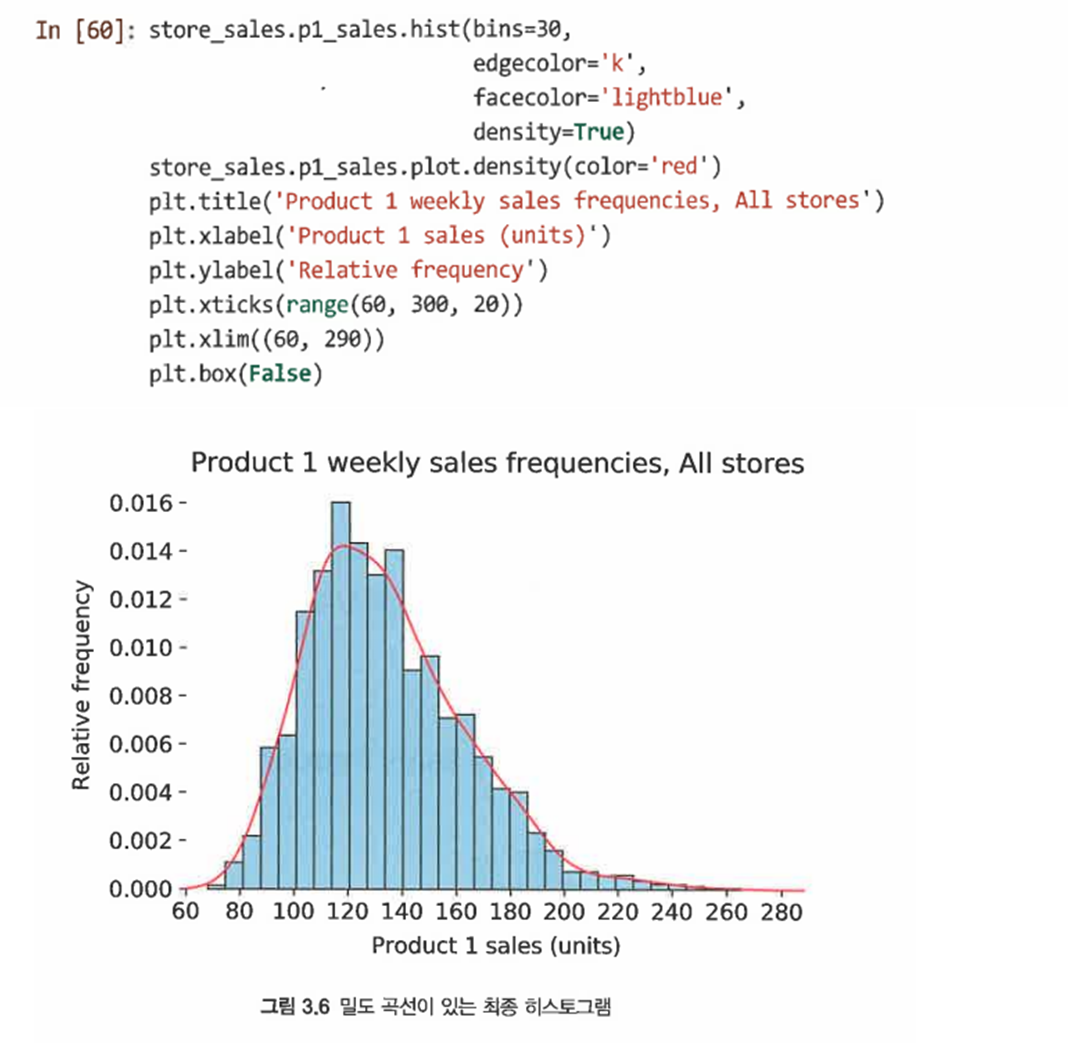
3.4.2 상자 그림
-
히스토그램보다 더 간결하게 분포 표시
-
box() 메서드를 사용해 레이블을 추가하고 vert=False 인수를 사용해 도면을 90도 회전시켜 보기 좋게 한다
-
sym='k.'를 사용하면 특이값 표식을 지정할 수 있다
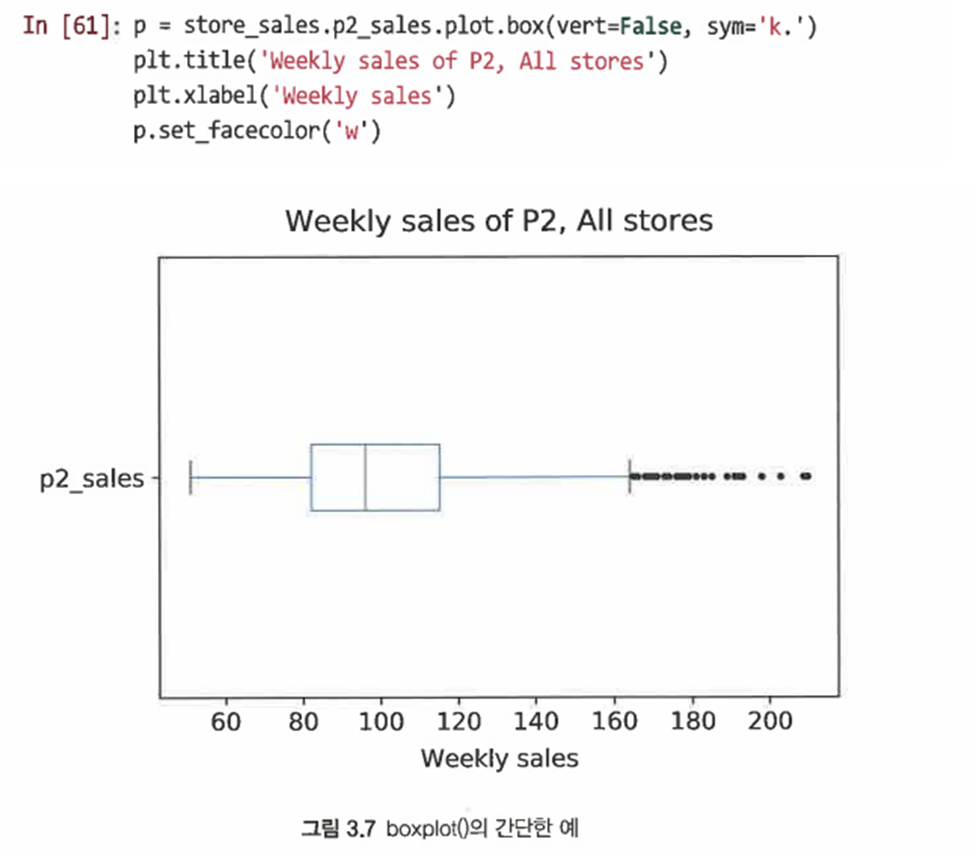
-
이 그림에서 중앙값은 중심선, 25번째&75번째 백분위수는 상자를 의미
-
바깥쪽 선은 상자에서 떨어진 상자 너비의 1.5배 이하인 가장 극단적인 값 지점의 '수염'
-
수염을 벗어난 포인트는 특이값
-
상자 그림은 다른 요인으로 분포를 비교할 때 훨씬 유용
-
다음과 같은 코드를 이용해 서로 다른 상점끼리 제품 2의 판매량을 비교할 수 있다
-
매장끼리 제품 2의 매출이 대략 비슷함을 확인할 수 있다
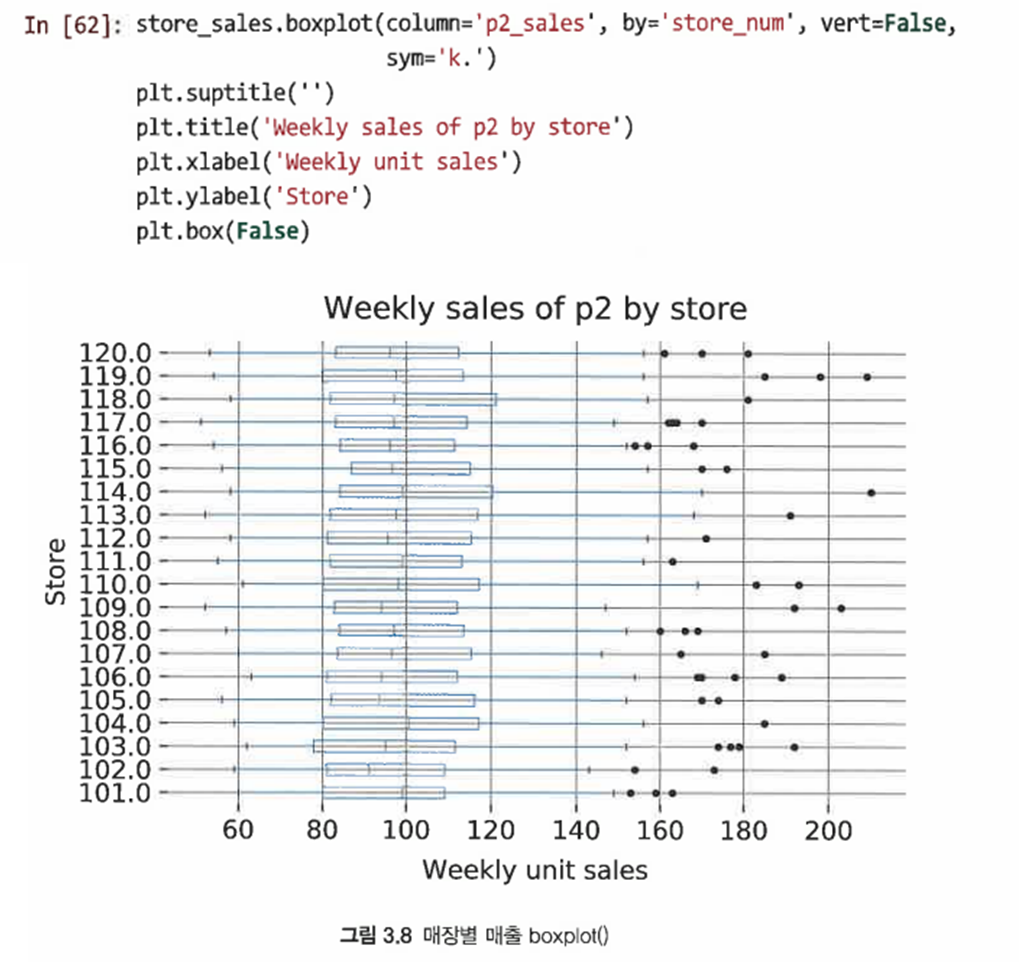
-
P2의 판매 단위가 비슷하지만, 매장 내 프로모션과 관련해 P2 판매가 다름을 알 수 있다
-
이 경우 설명 변수는 P2의 판촉 변수가 되므로 이제 boxplot()을 사용해 store_num을 판촉 변수 p2_promo로 대체한다
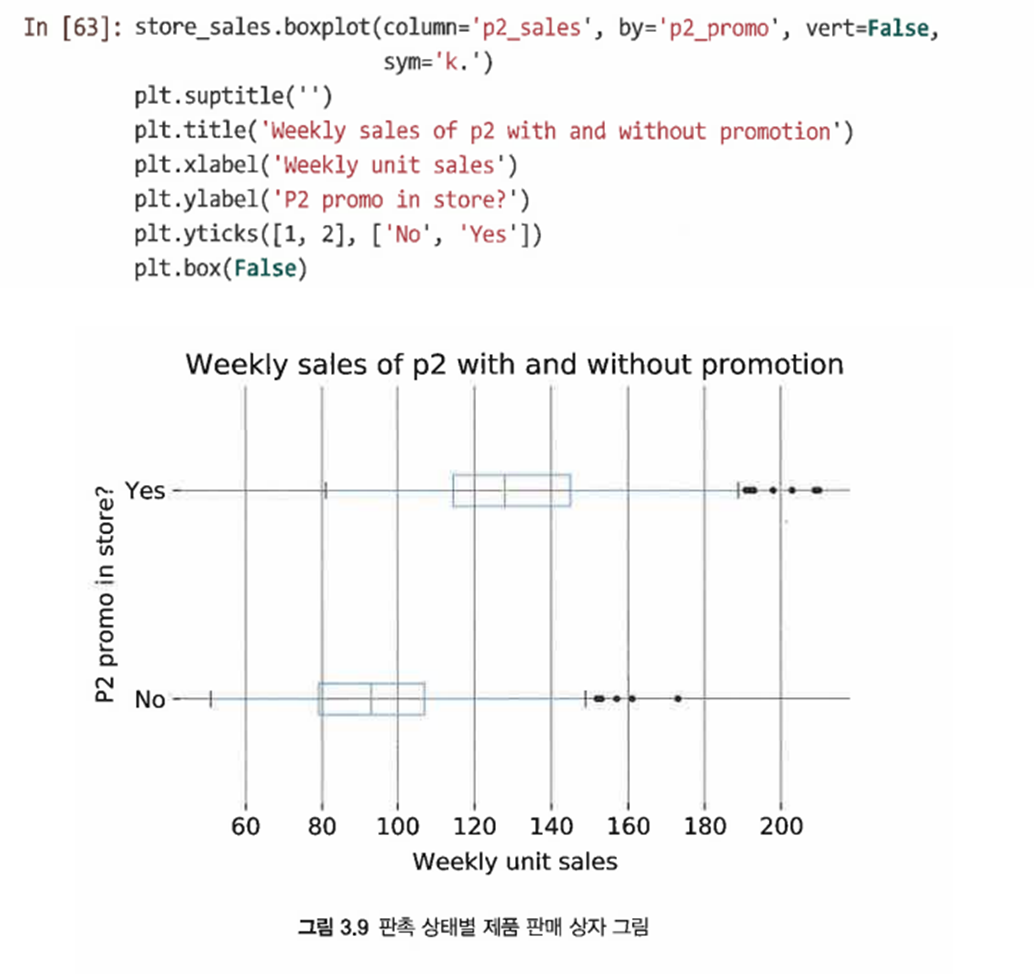
3.4.3 정규성 확인을 위한 QQ 도면*
- 분위수-분위수(QQ) 도면은 데이터의 모집단에 대해 추정한 분포가 맞는지 확인해보는 좋은 방법이다
- 데이터의 관측된 분위수를 정규 분포를 따를 경우 예상되는 분위수에 대비해 도식화해봄으로써 분포가 실제로 정규 분포인지 확인할 수 있다
- 데이터와 지정된 분포를 비교해주는 scipy.stats 라이브러리의 probplot() 함수 사용
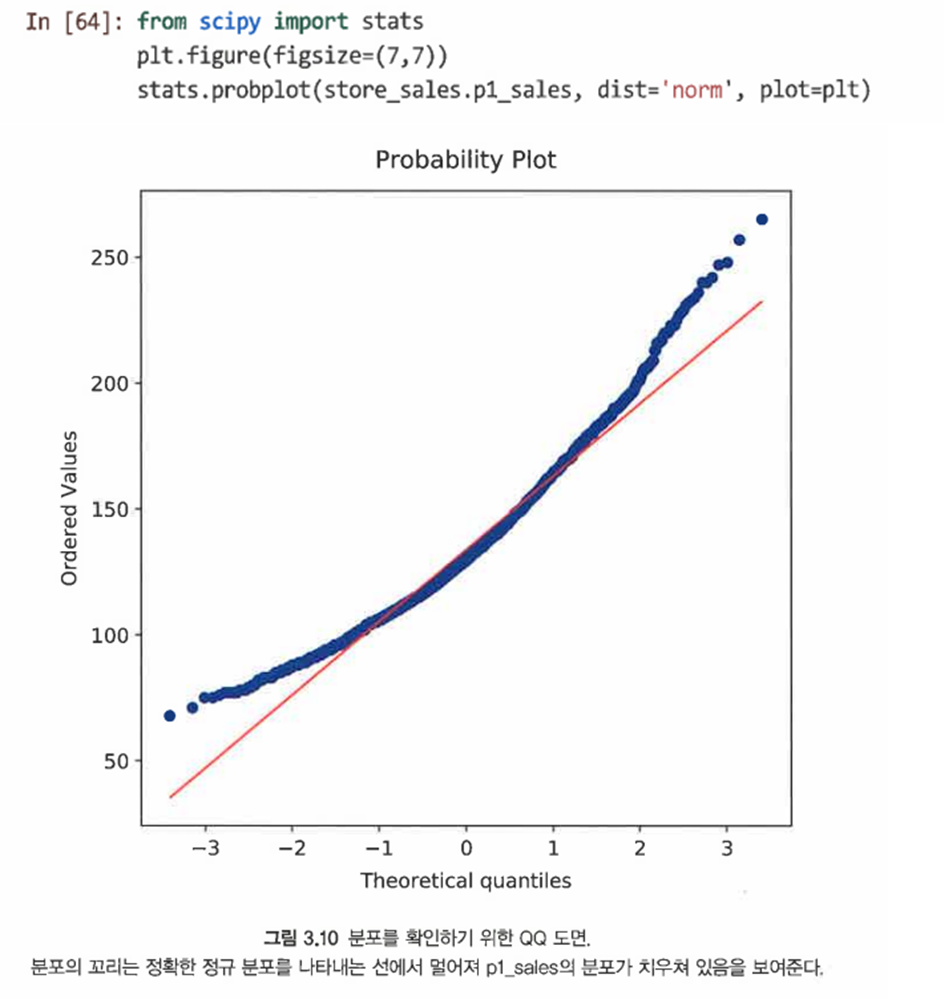
- p1_sales 분포는 끝선 부분에서 멀리 떨어져 있어 데이터가 정규 분포를 따르지 않음을 나타낸다
- 이 경우 log()를 사용해 데이터를 변환한다
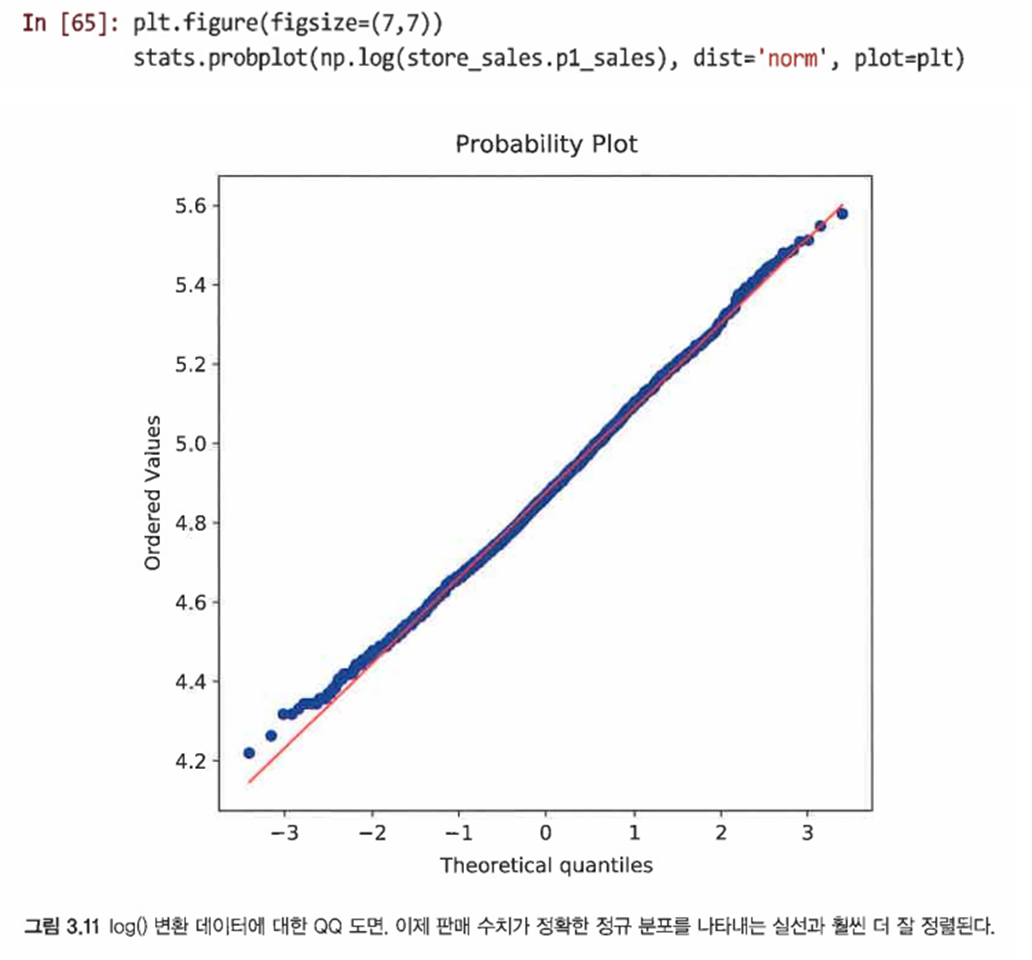
- 점이 실선에 훨씬 가까워서 변환 전 변수보다는 거의 정규임을 확인할 수 있다
- 이처럼 scipy.stats.probplot()을 정기적으로 사용해 데이터 분포에 대한 가정을 검정하는 것이 좋다
3.4.4 누적 분포*
- 경험적 누적 분포 함수(ECDF): 분포를 검사하고 백분위수 값을 읽는 쉬운 방법
- statsmodel 모델 라이브러리에서 ECDF() 함수를 사용
- 이 경우 P1의 주간 매출의 90%보다 높은 값을 알고 싶다고 가정한다
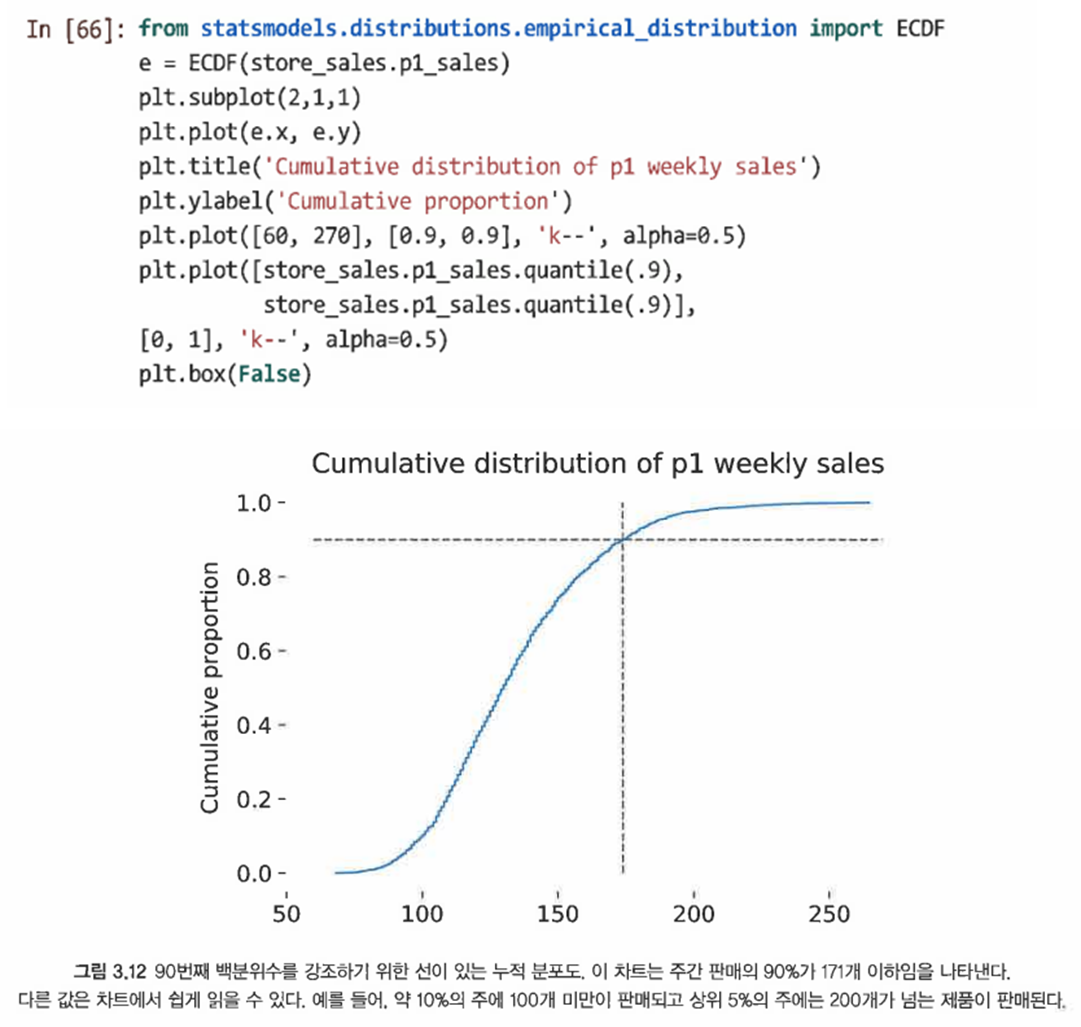
3.4.5 지도
-
cartopy 라이브러리의 cartopy 함수를 사용해 데이터를 지도에 중첩할 수 있다

-
그러나 이러한 등치도는 지리적 영역과 축척된 수량이 혼동이 오기 쉽기 때문에 주의할 필요가 있다
3.5 요점
- 다음 지침은 데이터를 정확하고 빠르게 설명하는데 도움이 된다

오 정리가 깔끔하네요 !