0. 들어가며
지난 포스팅에서는 Logistic Regression Model을 간단하게 알아보았다.
오늘은 Logistic Regression Model에서의 parameter 추정을 어떻게 하는지에 관하여 알아볼 예정이다.
1. β1의 해석
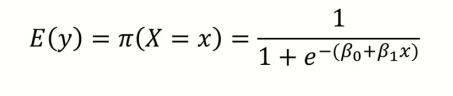
Logistic Regression Model은 선형적인 모델이 아니기 때문에 β1을 직관적으로 해석하기에 어려움이 있다.
따라서 parameter를 직관적으로 추정하기 위해 Odds라는 개념을 알아야 할 필요가 있다.
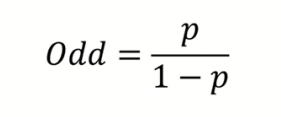
Odds : 성공확률을 p로 정의할 때, 실패 대비 성공 확률 비율
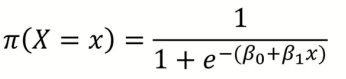
Logistic Regression Model은 위와 같았고, 해당 모델의 output 범위는 0 <= π <= 1였다.
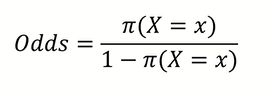
이때, Odds는 위와 같이 정의 할 수 있다.
다시 말해, 범주 0에 속할 확률 대비 범주 1에 속할 확률을 의미한다.

방금 구한 Odds에 log를 취하면 위 사진처럼 선형적으로 식이 도출되고, parameter를 직관적으로 해석할 수 있게 된다.
그리고 위의 과정을 Logit Transform이라 한다.
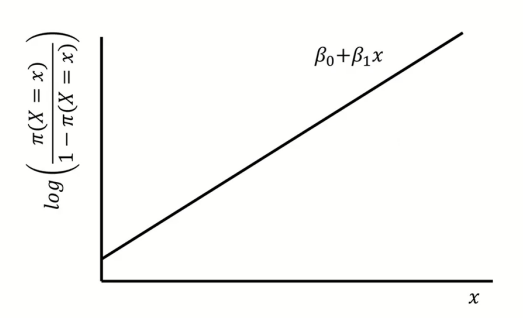
log(Odds)를 x에 대한 그래프로 그리면 위와 같고,
결국 β1은 x가 한 단위 증가했을 때 log(Odds)의 증가량을 의미한다.
2. 중간 요약
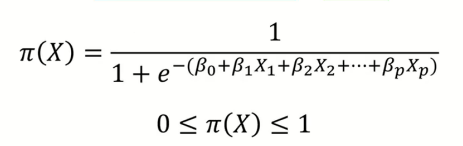
이쯤에서 Logistic Regression Model을 요약해서 한 번 정리하자면
- X변수를
Logistic fuction의 형태(비선형 결합)로 표현 - 관측치가 특정 범주에 속할 확률로 계산
- 확률값이 정해진 기준값보다 크면 범주1 아니면 범주2
Logistic Regression Model은 비선형적인 모델이기 때문에 parameter의 해석을 직관적으로 하기 위하여 Odds의 log를 취하는 방법을 이용
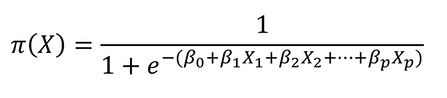
만약, 입력 변수 X가 2개 이상이면 Logistic Regression Model은 위처럼 식을 세울 수 있다.
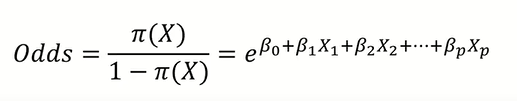
Odds를 취했을 때의 식은 위와 같고,
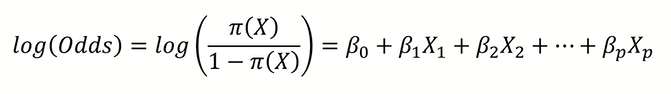
Odds에 log를 취하면 위와 같이 선형 결합의 형태로 식이 도출되어 parameter의 해석이 직관적이게 된다.
3. 파라미터 추정
Linear Regression Model에서의 parameter는 LSE(Least Square Estimation)를 사용하여 추정하였다.
Logistic Regression Model에서는 MLE(Maximum Likelihood Estimation)라는 방법을 사용하여 parameter를 추정한다.
- Linear Regression Model -> LSE (Least Square Estimation)
- Logistic Regression Model -> MLE(Maximum Likelihood Estimation)
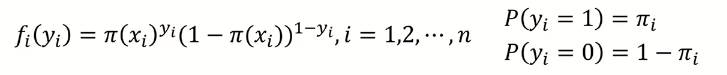
Logistic Regression Model의 배경을 설명할 때, 출력 변수 Y는 Bernoulli 분포를 따른다고 말한 적이 있었다.
그렇기 때문에 Bernoulli 분포를 따르는 확률 함수(pmf)는 위와 같이 정의할 수 있다.
(확률함수의 식이 이해가 되지 않는다면 통계쪽 공부를 더 하기를 바란다.)
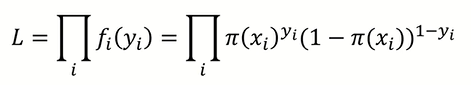
확률함수는 다시 위와 같은 likelihood 식으로 쓸 수 있다.
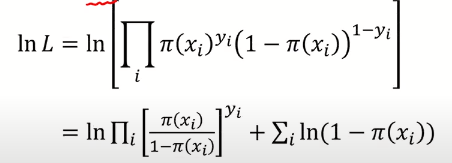
likehood 식은 모든 식들이 곱연산으로 적혀있음을 알 수 있는데, 곱연산이 아닌 합연산의 표현으로 식을 적기 위하여 log를 취하고 식을 정리했다.
cf) parameter를 추정하는 방법으로 주로 미분을 사용하는데 곱으로 표현된 식은 덧셈으로 표현된 식에 비하여 미분이 어렵기 때문
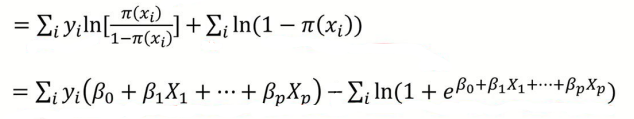
식을 전부 정리하고 나면 위와 같은 식으로 정리된다.
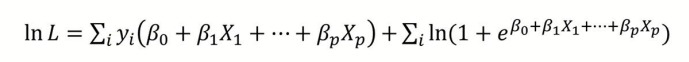
최종적으로 위 log likelihood function이 최대가 되는 파라미터 β를 결정하는 것이 목표이다.
그러나 log likelihood function은 파라미터 β에 대하여 비선형이므로 Linear Regression Model과 다르게 명시적인 해가 존재하지 않다. (No closed-form solution)
따라서 Iterative reweight least square, Conjugate gradient, Newton's method 등의 수치 최적화 알고리즘을 이용하여 해를 구한다.
4. Logistic Regression Model 결과
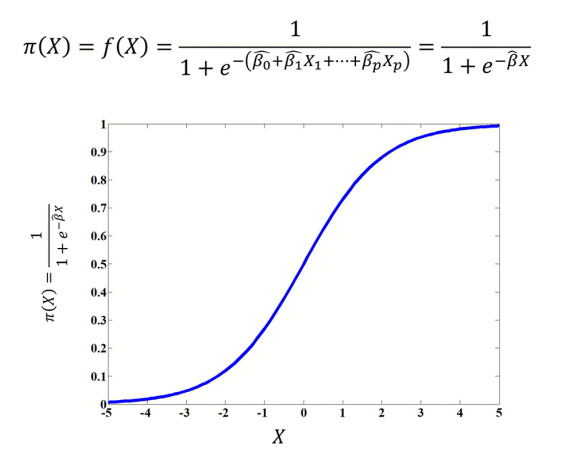
파라미터가 추정되고 난 이후 최종모델은 위와 같이 나타낼 수 있다.
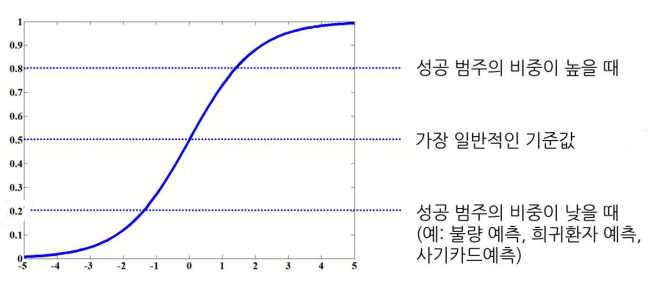
최종모델을 도출했으면 이제 이진 분류를 위한 기준값(threshold)를 설정해야 한다.
일반적으로 0.5를 사용하고, 예를 들어 0.5보다 작은 값이 나오면 불량품으로 0.5보다 큰 값이 나오면 정상으로 분류하는 것이다.
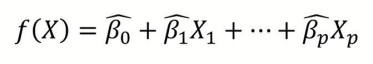
Linear Regression Model에서는 입력변수 X가 1단위 증가할 때, 출력변수 Y의 변화량을
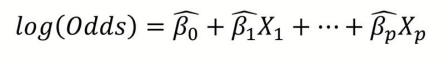
Logistic Regression Model에서는 입력변수 X가 1단위 증가할 때, log Odds의 변화량을 나타낸다.
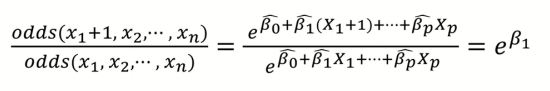
Logistic Regression Model의 결과를 분석할 때, Odds Ratio라는 방법을 이용하여 분석하기도 한다.
- 나머지 입력 변수는 모두 고정시킨 상태에서 한 변수를 1단위 증가시켰을 때 변화하는 Odds의 비율
- 예를 들어, 위 사진에서 X1이 1단위 증가하면 성공에 대한 Odds Ratio가 exp(β1)만큼 변화한다
5. 마치며
오늘은 Logistic Regression Model의 parameter를 추정하는 방법에 대하여 알아보았다.
다음 포스팅에서는 Logistic Regression Model 예제를 적으려고 한다.
또한 필자는 고려대학교 김성범 교수님이 운영하시는 유튜브 채널을 보고 공부한 내용을 포스팅 하였으므로 아래 출처를 남긴다.
https://www.youtube.com/@user-yu5qs4ct2b
