1. 시그모이드 함수(Sigmoid function)
Logistic Regression Model에서는 sigmoid function이 사용되기 때문에 sigmoid function에 대하여 알아보아야 한다.
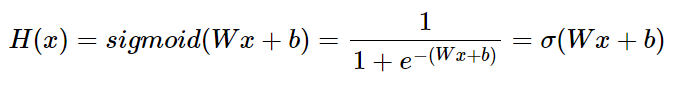
Logistic Regression Model은 위와 같은 식을 가지고, 선형회귀에서와 마찬가지로 최적의 W와 b를 찾는 것이 목표이다.
그렇다면 지금부터 W와 b가 함수의 그래프에 어떤 영향을 주는지 pytorch를 이용하여 알아보겠다.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt# 시그모이드 함수 정의
def sigmoid(x):
return 1/(1+np.exp(-x))우선 필요한 Module을 설정하고 Sigmoid function을 함수로 정의하였다.
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y, 'g')
plt.plot([0, 0], [1.0, 0.0], ':') # 점선 추가
plt.title('Sigmoid Function')
plt.show()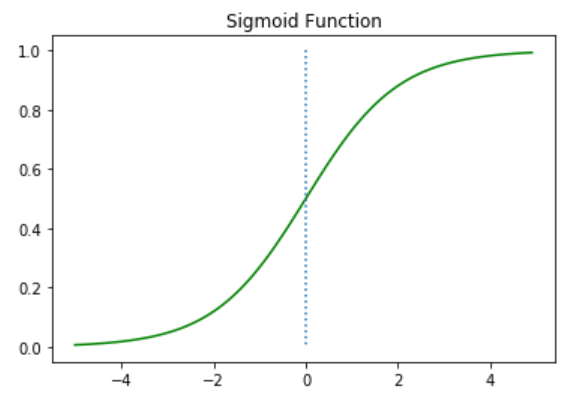
가장 먼저 W가 1이고 b가 0인 그래프를 그려보았다.
위의 그래프를 통해서 Sigmoid function은 output을 0과 1사이의 값으로 조정하여 반환함을 알 수 있다.
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(0.5 * x)
y2 = sigmoid(x)
y3 = sigmoid(2*x)
plt.plot(x, y1, 'r', linestyle='--') # W = 0.5
plt.plot(x, y2, 'g', linestyle='--') # W = 1
plt.plot(x, y3, 'b', linestyle='--') # W = 2
plt.plot([0,0], [1,0], ':') # 점선 추가
plt.title('Sigmoid Function')
plt.show()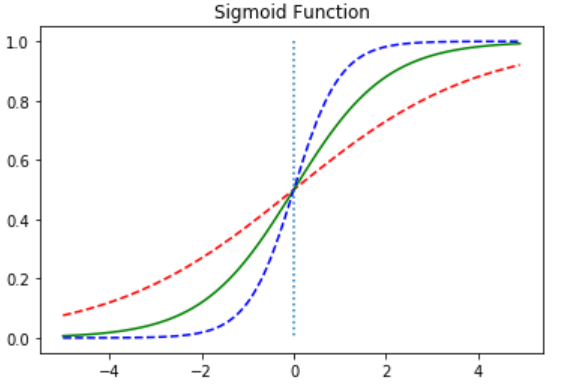
이번에는 W값을 변화시키면서 그래프를 확인해보았다.
그래프를 보면 W가 커질 수록 그래프의 기울기가 커짐을 알 수 있다.
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x + 0.5)
y2 = sigmoid(x + 1)
y3 = sigmoid(x + 1.5)
plt.plot(x, y1, 'r', linestyle='--') # x + 0.5
plt.plot(x, y2, 'g') # x + 1
plt.plot(x, y3, 'b', linestyle='--') # x + 1.5
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()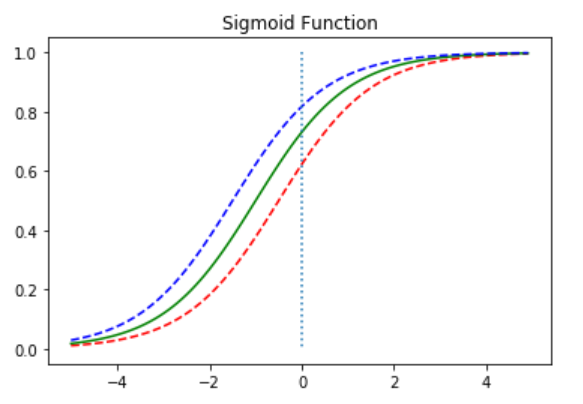
이번에는 b값의 변화에 따라 그래프가 어떻게 이동하는지를 알아보았다.
b가 커질수록 그래프가 위로 이동함을 알 수 있다. (y축 방향으로 평행이동)
2. 비용 함수(Cost function)
이제 Logistic Regression Model이 Sigmoid function을 포함하는 것은 알았다.
이제 최적의 W와 b를 찾을 수 있는 Cost function을 정의해야 한다.
그렇다면 로지스틱 회귀도 앞서 배웠던 선형 회귀에서의 비용함수인 MSE를 사용하면 안 될까?
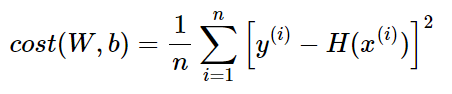
위는 선형 회귀에서 사용했던 MSE의 수식이다.
위의 비용 함수 수식에서 모델은 이제 H(x) = Wx + b가 아니라 H(x) = sigmoid(Wx + b)이다.
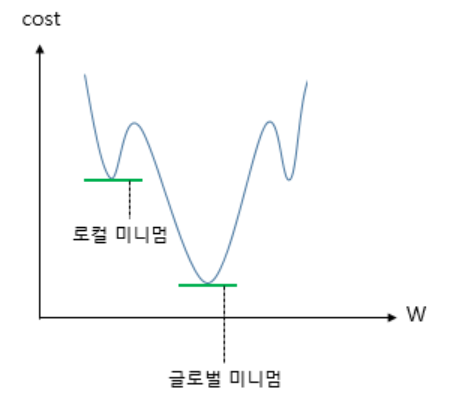
그리고 이 비용 함수를 미분하면 위와 같이 유사한 non-convex 형태의 그래프가 그려진다.
위와 같은 그래프에서 경사 하강법을 사용할 경우 문제점은 오차가 최소가 되는 구간에 도착했다고 판단한 그 구간이 Global Minimum이 아닌 Local Minimum일 수도 있다는 점이다.
이는 cost가 최소가 되는 가중치 W를 찾는다는 비용 함수의 목적에 적합하지 않다.
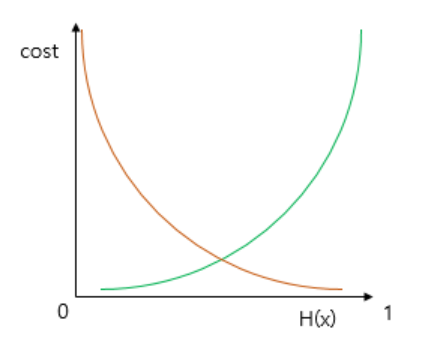
sigmoid function의 특징은 output이 0과 1사이의 값이라는 점이다. 즉, 실제값이 1일 때 예측값이 0에 가까워지면 오차가 커져야 하며, 실제값이 0일 때, 예측값이 1에 가까워지면 오차가 커져야 한다.
그리고 이를 충족하는 함수가 바로 로그 함수이다.
위는 y=0.5에 대칭하는 두 개의 로그 함수 그래프이다.
실제값이 1일 때의 그래프를 주황색, 실제값이 0일 때의 그래프를 초록색 선으로 표현하였다.
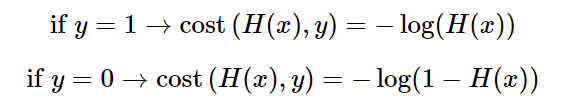
위 두 개의 로그함수를 수식으로 표현하면 위와 같이 나타낼 수 있다.
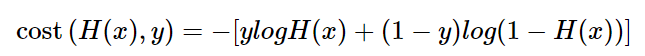
또한, 이는 하나의 식으로 합쳐서 작성할 수 있다.
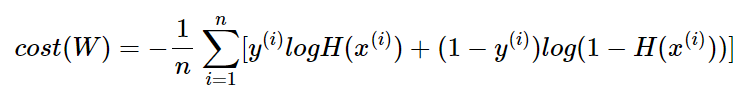
선형 회귀에서는 모든 오차의 평균을 구하여 평균 제곱 오차를 사용했었다. 마찬가지로 로지스틱 회귀에서도 모든 오차의 평균을 구하면 위와 같은 식으로 정리할 수 있다.
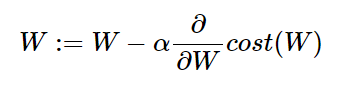
이제 위 비용 함수에서 경사 하강법을 진행하면서 최적의 가중치 W를 구하면 된다.
3. 파이토치로 로지스틱 회귀 구현
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)우선 필요한 모듈들을 import 해준다.
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
print(x_train.shape)
print(y_train.shape)torch.Size([6, 2])
torch.Size([6, 1])x_train과 y_train을 텐서로 선언하고, 각각의 크기를 확인해보았다.
x_train은 6x2의 크기를 가지는 행렬, y_train은 6x1의 크기를 가지는 벡터임을 알 수 있다.
W = torch.zeros((2, 1), requires_grad=True) # 크기는 2 x 1
b = torch.zeros(1, requires_grad=True)x_train을 X, 이에 곱해지는 가중치 벡터를 W라고 하였을 때, XW가 성립되기 위해서는 W벡터의 크기가 2x1이어야 한다.
hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))
# hypothesis = torch.sigmoid(x_train.matmul(W) + b)이제 모델을 선언한다.
pytorch에서는 sigmoid function을 이미 구현하여 제공하기 때문에 주석처리 되어있는 코드를 사용해도 무방하다.
print(hypothesis)tensor([[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000]], grad_fn=<MulBackward>)앞서 W와 b는 torch.zeros를 통해 전부 0으로 초기화 된 상태이다.
이 상태에서 예측값을 출력해보면 y_train과 크기가 동일한 6x1의 크기를 가지는 예측값 벡터가 나오고 모든 값이 0.5이다.
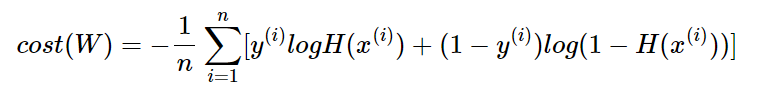
이제 위에서 구한 비용 함수를 이용하여 현재 예측값과 실제값 사이의 cost를 구해보겠다.
print(hypothesis)
print(y_train)tensor([[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000]], grad_fn=<MulBackward0>)
tensor([[0.],
[0.],
[0.],
[1.],
[1.],
[1.]])그 전에 먼저 현재 예측값과 실제값을 출력해보았다.
losses = -(y_train * torch.log(hypothesis) + (1-y_train) * torch.log(1-hypothesis))
# F.binary_cross_entropy(hypothesis, y_train)
print(losses)tensor([[0.6931],
[0.6931],
[0.6931],
[0.6931],
[0.6931],
[0.6931]], grad_fn=<NegBackward0>)이제 모든 데이터에 대하여 오차를 구해보면 위와 같이 나온다.
또한, pytorch에서는 로지스틱 회귀 모델에서의 cost function을 구현해놓았기 때문에 주석 처리된 코드를 사용해도 무방하다.
cost = losses.mean()
print(cost)tensor(0.6931, grad_fn=<MeanBackward0>)그리고 이 전체 오차에 대한 평균을 구하면 cost는 0.6931로 나온다.
4. 전체코드
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
# Dataset 정의
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
# cost 계산
cost = F.binary_cross_entropy(hypothesis, y_train)
# 최적화
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))Epoch 0/1000 Cost: 0.693147
Epoch 100/1000 Cost: 0.134722
Epoch 200/1000 Cost: 0.080643
Epoch 300/1000 Cost: 0.057900
Epoch 400/1000 Cost: 0.045300
Epoch 500/1000 Cost: 0.037261
Epoch 600/1000 Cost: 0.031672
Epoch 700/1000 Cost: 0.027556
Epoch 800/1000 Cost: 0.024394
Epoch 900/1000 Cost: 0.021888
Epoch 1000/1000 Cost: 0.019852학습이 끝났고, 이제 훈련했던 훈련데이터를 그대로 입력했을 때, 제대로 예측하는지 확인해보겠다.
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
print(hypothesis)tensor([[2.7648e-04],
[3.1608e-02],
[3.8977e-02],
[9.5622e-01],
[9.9823e-01],
[9.9969e-01]], grad_fn=<SigmoidBackward0>)현재 위 값들은 0과 1사이의 값을 가지고 있다.
이제 0.5를 넘으면 True, 넘지 않으면 False로 값을 정하여 출력해보겠다.
prediction = hypothesis >= torch.FloatTensor([0.5])
print(prediction)tensor([[False],
[False],
[False],
[ True],
[ True],
[ True]])실제값은 [[0], [0], [0], [1], [1], [1]]이므로, 이는 결과적으로 False, False, False, True, True, True와 동일하다.
즉, 기존의 실제값과 동일하게 예측이 된 것을 볼 수 있다.
print(W)
print(b)tensor([[3.2530],
[1.5179]], requires_grad=True)
tensor([-14.4819], requires_grad=True)훈련이 된 후의 parameter W와 b를 출력해보면 위와 같다.
