03-01 선형회귀(Linear Regression)

박건·2023년 8월 27일

AI Deep Learning Linear Regression PyTorch machine learning 딥러닝 머신러닝 선형회귀 인공지능 파이토치

1. 기본 셋팅

2. 훈련/테스트 데이터 선언

cf) optimizer.zero_grad()가 필요한 이유

7. 전체 코드

Pytorch로 시작하는 딥러닝 입문

목록 보기

2/10

1. 기본 셋팅

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 같은 결과가 도출되도록 random seed를 1로 고정시킴
torch.manual_seed(1)

2. 훈련/테스트 데이터 선언

# x_train, y_train 변수를 torch.FloatTensor를 이용하여 선언
x_train = torch.FloatTensor([[1],
                             [2],
                             [3]])
y_train = torch.FloatTensor([[2],
                             [4],
                             [6]])

# x_train 출력 및 크기 체크
print(x_train)
print(x_train.shape)

tensor([[1.],
        [2.],
        [3.]])
torch.Size([3, 1])

x_train의 값이 출력되고, 크기는 3x1임을 알 수 있다.

# y_train 출력 및 크기 체크
print(y_train)
print(y_train.shape)

tensor([[2.],
        [4.],
        [6.]])
torch.Size([3, 1])

y_train의 값이 출력되고, 크기는 3x1임을 알 수 있다.

3. 가중치와 편향 초기화

Linear Regression 이란 학습 데이터와 가장 fit한 하나의 직선을 찾는 일이다.
그리고 가장 fit한 직선을 정의하는 것은 W와 b이다.

따라서 Linear Regression 의 목표는 가장 fit한 직선을 정의하는 W와 b의 값을 찾는 것이다.

W = torch.zeros(1, requires_grad=True)
print(W)

tensor([0.], requires_grad=True)

가중치 W를 0으로 초기화하고 학습을 통해 값이 변경되는 변수임을 명시
requires_grad=True는 W 변수가 학습을 통해 계속 값이 변경되는 변수임을 의미

b = torch.zeros(1, requires_grad=True)
print(b)

tensor([0.], requires_grad=True)

편향 b도 0으로 초기화하고, 학습을 통해 값이 변경되는 변수임을 명시

현재 가중치 W, b는 모두 0이므로 현 모델의 식은 다음과 같다.

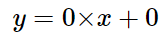
x에 어떤 값이 들어가도 모델은 0을 예측하는 상태이므로, 아직 적절한 W와 b가 아니다.

4. 가설 세우기

hypothesis = x_train * W + b
print(hypothesis)

tensor([[0.],
        [0.],
        [0.]], grad_fn=<AddBackward0>)

가설(모델)의 식을 세웠다.

5. 비용 함수 선언

Linear Regression 에서의 Cost function 은 다음과 같다.

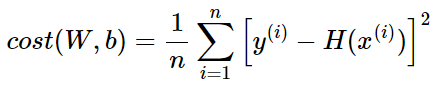
cost = torch.mean((hypothesis - y_train) ** 2)
print(cost)

tensor(18.6667, grad_fn=<MeanBackward1>)

6. Optimizer 선언

이제 optimizer를 설정하면 된다. 여기서는 optimizer중 하나인 SGD 를 사용한다.
lr 은 learning rate를 의미하고, 학습 대상인 W 와 b가 SGD의 입력이 된다.

optimizer = optim.SGD([W, b], lr=0.01)

# gradient를 0으로 초기화
optimizer.zero_grad() 
# 비용 함수를 미분하여 gradient 계산
cost.backward() 
# W와 b를 업데이트
optimizer.step()

cf) optimizer.zero_grad()가 필요한 이유

파이토치는 미분을 통해 얻은 기울기를 이전에 계산된 값에 누적시키는 특징이 있다. 예를 들어보자

# ex1)
import torch
w = torch.tensor(2.0, requires_grad=True)

nb_epochs = 5
for epoch in range(nb_epochs + 1):
    z = 3*w

    z.backward()
    print('수식을 w로 미분한 값 : {}'.format(w.grad))

수식을 w로 미분한 값 : 3.0
수식을 w로 미분한 값 : 6.0
수식을 w로 미분한 값 : 9.0
수식을 w로 미분한 값 : 12.0
수식을 w로 미분한 값 : 15.0
수식을 w로 미분한 값 : 18.0

# ex2)
import torch
w = torch.tensor(2.0, requires_grad=True)

nb_epochs = 5
for epoch in range(nb_epochs + 1):
    z = 7*w*w

    z.backward()
    print('수식을 w로 미분한 값 : {}'.format(w.grad))

수식을 w로 미분한 값 : 28.0
수식을 w로 미분한 값 : 56.0
수식을 w로 미분한 값 : 84.0
수식을 w로 미분한 값 : 112.0
수식을 w로 미분한 값 : 140.0
수식을 w로 미분한 값 : 168.0

7. 전체 코드

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1) # 현재 실습하는 코드를 재실행해도 같은 결과가 나오도록 랜덤 시드를 부여

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])

# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# optimizer 초기화
optimizer = optim.SGD([W,b], lr=0.01)

# 에폭 설정 (원하는 만큼 경사 하강법 반복)
nb_epochs = 2000
for epoch in range(1, nb_epochs + 1):
    # H(x) 계산
    hypothesis = x_train * W + b

    # cost 계산
    cost = torch.mean((y_train - hypothesis) ** 2)

    # 최적화
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(epoch, nb_epochs, W.item(), b.item(), cost.item()))

Epoch  100/2000 W: 1.745, b: 0.579 Cost: 0.048403
Epoch  200/2000 W: 1.800, b: 0.456 Cost: 0.029910
Epoch  300/2000 W: 1.842, b: 0.358 Cost: 0.018483
Epoch  400/2000 W: 1.876, b: 0.281 Cost: 0.011421
Epoch  500/2000 W: 1.903, b: 0.221 Cost: 0.007058
Epoch  600/2000 W: 1.923, b: 0.174 Cost: 0.004361
Epoch  700/2000 W: 1.940, b: 0.137 Cost: 0.002695
Epoch  800/2000 W: 1.953, b: 0.107 Cost: 0.001665
Epoch  900/2000 W: 1.963, b: 0.084 Cost: 0.001029
Epoch 1000/2000 W: 1.971, b: 0.066 Cost: 0.000636
Epoch 1100/2000 W: 1.977, b: 0.052 Cost: 0.000393
Epoch 1200/2000 W: 1.982, b: 0.041 Cost: 0.000243
Epoch 1300/2000 W: 1.986, b: 0.032 Cost: 0.000150
Epoch 1400/2000 W: 1.989, b: 0.025 Cost: 0.000093
Epoch 1500/2000 W: 1.991, b: 0.020 Cost: 0.000057
Epoch 1600/2000 W: 1.993, b: 0.016 Cost: 0.000035
Epoch 1700/2000 W: 1.995, b: 0.012 Cost: 0.000022
Epoch 1800/2000 W: 1.996, b: 0.010 Cost: 0.000014
Epoch 1900/2000 W: 1.997, b: 0.008 Cost: 0.000008
Epoch 2000/2000 W: 1.997, b: 0.006 Cost: 0.000005