1. 주변 분할표와 조건부 분할표

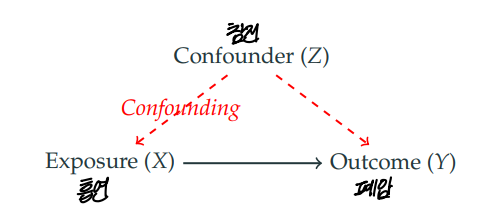
1-1. 교락변수, 교락효과

• 임상시험의 경우 실험군과 통제군을 제외한 모든 변수를 통제한다.
• 하지만, 대부분의 사회과학연구는 관찰연구로 진행되기 때문에 변수를 통제하기 어렵다.
• 독립변수와 반응변수 모두에 영향을 미치는 교락변수 (confounder)가 존재할 수 있으며, 교락변수에 의한 영향을 교락효과 (confounding effect)라 한다.

1-2. 주변 분할표와 주변 오즈비

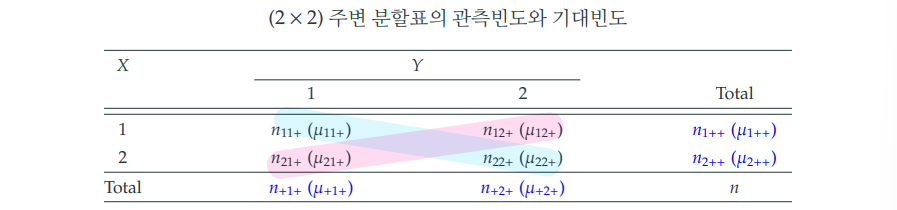
주변 분할표 (marginal tables)

Z의 수준을 고려하지 않은 X와 Y변수 2차원의 형태로 표현한 분할표이다.
이때, Z 자리에 전부 + 표기를 한다.

주변 오즈비 (marginal odds ratio)

$(2 \times 2)$ 주변 분할표에서 구한 오즈비

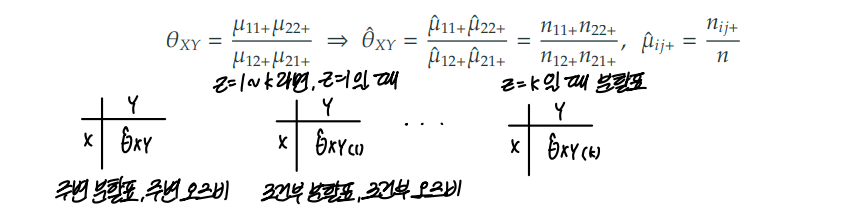
1-3. 조건부 분할표와 조건부 오즈비

조건부 분할표 (conditional tables)

Z의 수준별로 정리한 X와 Y변수 2차원 분할표

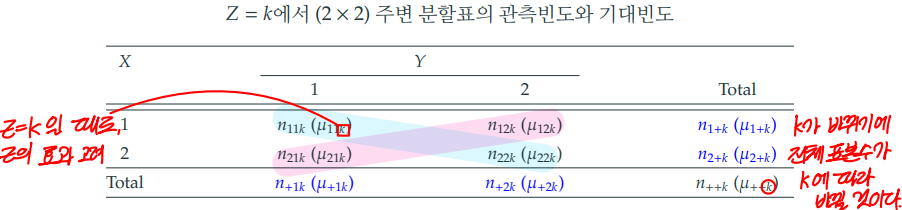
주변 분할표와 다르게 세 번째 자리에 k로 Z의 수준을 고려한다.
Z=k로 k값이 변화하면 전체 표본수도 k값에 따라 바뀔 것이다.

조건부 오즈비 (conditional odds ratio)

Z=k일 때, $(2 \times 2)$ 주변 분할표에서 구한 오즈비

---

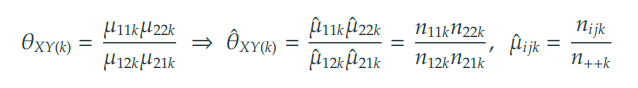
2. 주변 독립성과 조건부 독립성

cf) 독립의 의미

• $X가 1일 때 오즈 \over Y가 1일 때 오즈 = 1$ 일 때 독립이다.
• 즉, "X가 1일 때 오즈"와 "Y가 1일 때 오즈"가 같다면 독립이다.
  
  

주변 독립성 (marginal independence)

Z 효과를 무시했을 때의 주변 분할표에서 X와 Y가 독립이다.

조건부 독립성 (conditional independence)

Z=k인 특정 분할표에서 X와 Y가 독립이다.

X와 Y가 1~K에 대해 모두 독립일 때, 조건부 독립일 경우 주변 독립인지 알 수 없다.

---

3. 예제 및 R 실습

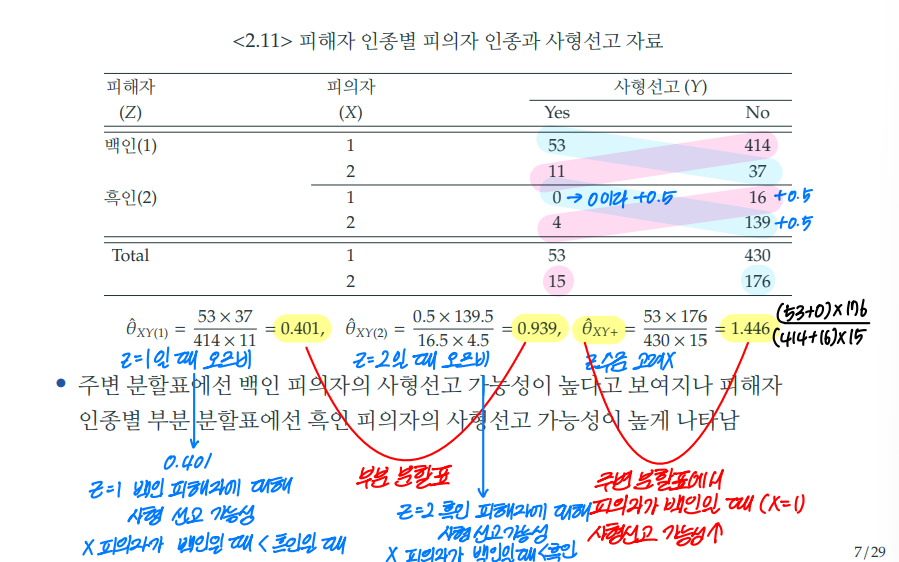
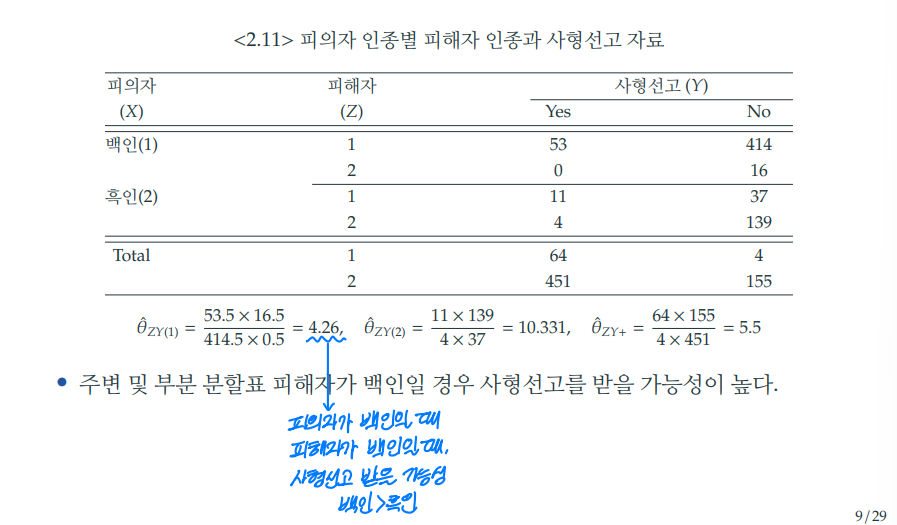
1) 피해자의 인종 기준 (Z)

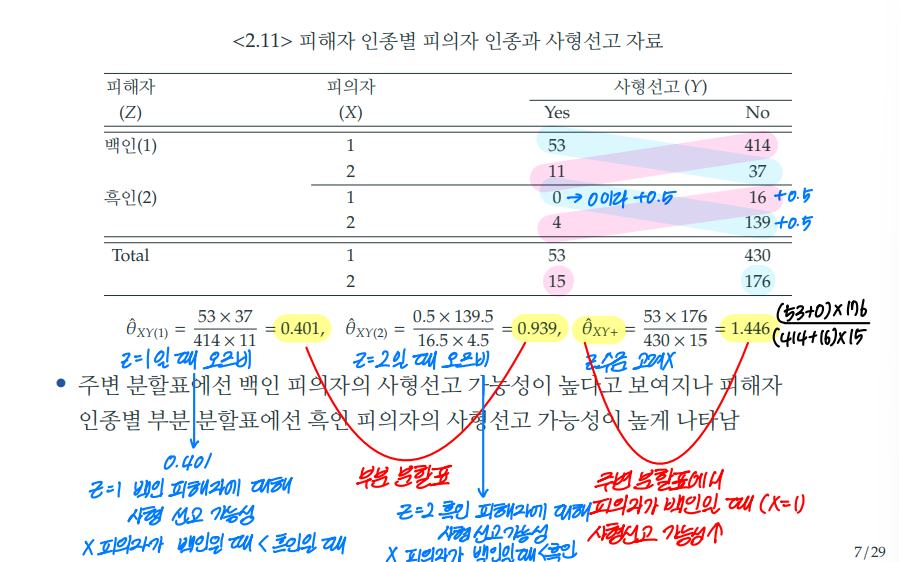
• 오즈비는 cross-product로 계산한다.

• 이때 피해자가 흑인일 때 (Z=2), 피의자가 백인일 때 (X=1), 사형선고를 받았을 때 (Y=Yes) 셀의 값이 0이기 때문에 Z=2일 때의 모든 셀에 0.5를 더하여 값을 보정한다.

• 오즈비 계산 & 보정 개념 참고 링크

• Z값에 대한 조건부 오즈비는 다음과 같다.

  • 피해자가 백인일 때 (Z=1) 오즈비 = 0.401
  • 피해자가 흑인일 때 (Z=2) 오즈비 = 0.939

• Z값을 고려하지 않은 주변 오즈비는 다음과 같다.

  • 피해자의 인종을 고려하지 않았을 때 (Z=+) 오즈비 = 1.446

✅ 오즈비의 해석

• 조건부 오즈비
  • 0.401 : Z=1일 때, 즉, 피해자가 백인일 때 & 피의자가 백인일 때 사형 선고 가능성이 피의자가 흑인일 때 사형 선고 가능성보다 작다는 것을 의미한다. 요약하면, 백인 피해자일 때 흑인 피의자의 사형 선고 확률이 더 크다.
  • 0.939 : Z=2일 때, 즉, 피해자가 흑인일 때 & 피의자가 백인일 때 사형 선고 가능성이 피의자가 흑인일 때 사형 선고 가능성보다 작다는 것을 의미한다. 요약하면, 흑인 피해자일 때 흑인 피의자의 사형 선고 확률이 더 크다.
    
    
• 주변 오즈비
  1.446 : 피해자의 인종을 고려하지 않았을 때, 피의자가 백인일 때 사형 선고 가능성이 피의자가 흑인일 때 사형 선고 가능성보다 크다는 것을 의미한다. 요약하면, 백인 피의자의 사형 선고 확률이 더 크다.
  
  
  ➡️ 피해자의 인종 (Z)을 고려하지 않았을 때는 백인의 사형 선고 확률이 더 크지만, 피해자의 인종을 고려했을 때는 흑인의 사형 선고 확률이 더 크게 나타난다.

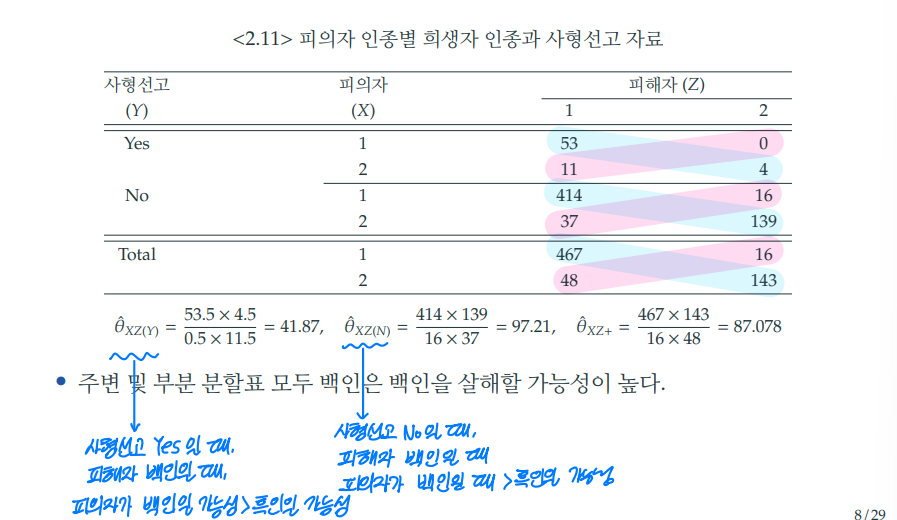
2) 사형 선고 기준 (Y)

3) 피의자 인종 기준 (X)

4) R 실습

• 데이터 생성

penalty <- array(c(53,11,414,37,0,4,16,139), dim = c(2, 2, 2),
dimnames = list("Defendant" = c("White", "Black"),
"Penalty" = c("Yes", " No"),
"Victim" = c("White", "Black")))
penalty
## , , Victim = White
##
## Penalty
## Defendant Yes No
## White 53 414
## Black 11 37
##
## , , Victim = Black
##
## Penalty
## Defendant Yes No
## White 0 16
## Black 4 139

• 피해자의 인종 기준 (Z)

library(vcd)
loddsratio(penalty, log = FALSE) # XY(z)
## odds ratios for Defendant and Penalty by Victim
##
## White Black
## 0.4208843 0.9393939
m.penalty <- margin.table(penalty, margin = c(1,2))
loddsratio(m.penalty, log = FALSE) # XY+
## odds ratios for Defendant and Penalty
##
## [1] 1.446202

• 신뢰구간

confint(loddsratio(penalty, log = FALSE))
## 2.5 % 97.5 %
## White 0.20498745 0.8641678
## Black 0.04838904 18.2367947
confint(loddsratio(m.penalty, log = FALSE))
## 2.5 % 97.5 %
## White:Black/Yes: No 0.7941306 2.633696

• 사형 선고 기준 (Y)

penalty.Y <- aperm(penalty, c(1,3,2))
loddsratio(penalty.Y, log = FALSE) # XZ(y)
## odds ratios for Defendant and Victim by Penalty
##
## Yes No
## 41.86957 93.45091
m.penalty.Y <- margin.table(penalty.Y, margin = c(1,2))
loddsratio(m.penalty.Y, log = FALSE) # XZ+
## odds ratios for Defendant and Victim
##
## [1] 86.95443

• 피의자 인종 기준 (X)

penalty.X <- aperm(penalty, c(3,2,1))
loddsratio(penalty.X, log = FALSE)
## odds ratios for Victim and Penalty by Defendant
##
## White Black
## 4.259349 9.506667
m.penalty.X <- margin.table(penalty.X, margin = c(1,2))
loddsratio(m.penalty.X, log = FALSE)
## odds ratios for Victim and Penalty
##
## [1] 5.498891

---

4. 심슨의 역설 (simpson's paradox)

• 교락변수(Z)로 인해 주변 연관성과 조건부 연관성의 해석이 다른 경우를 의미한다.
  • 주변 연관성 : 백인 피의자의 사형 선고 가능성이 높다.
  • 조건부 연관성 : 희생자의 인종과 관계없이 흑인 피의자의 사형 선고 가능성이 높다.
• 주변 연관성과 조건부 연관성의 결과가 다르게 나타나는 이유는 "피해자의 인종(Z)과 피의자의 인종(X)간 강한 연관성이 존재하기 때문이다.
  $\hat\theta_{XZ+} \approx 87$
• 피해자가 백인인 경우(Z=1), 사형 선고 판결 (Y=1)이 더 자주 발생하는 경향이 있다.
  $\hat\theta_{ZY+} \approx 6$
  
  

R 실습

mosaic(m.penalty)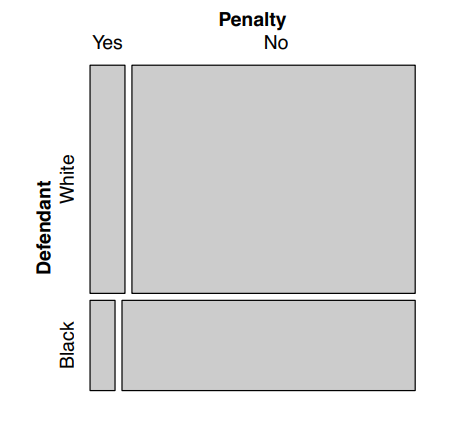

strtab = structable(Victim ~ Defendant + Penalty, data = penalty)
cotabplot(strtab)

---

💡 질문과 피드백은 댓글에 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.