[Categorical Data Analysis] 4. 독립성 검정 (Pearson, LRT, standardized residual, Fisher's exact test) 개념 및 R 실습
1. 이차원 분할표의 기대빈도
범주형 데이터의 독립성 검정을 위해서 범주형 데이터가 표현되는 형태인 "이차원 분할표"의 기대빈도와 관련된 개념이 필요하다.
1-1. 독립성 검정을 위한 귀무가설
독립성 검정을 위한 귀무가설은 다음과 같이 정의할 수 있다.

1-2. 귀무가설 하에서 기대빈도 (expected frequency)
귀무가설 하에서 즉, 와 가 독립일 때, 기대빈도는 다음과 같이 정의된다.
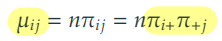
이고 일 때의 확률 ()는 이고 로 나올 확률 곱하기 실제 이고 로 나온 횟수이다.
귀무가설 하에서 와 가 독립이므로 이고 로 나올 확률은 일 확률 곱하기 일 확률이다.
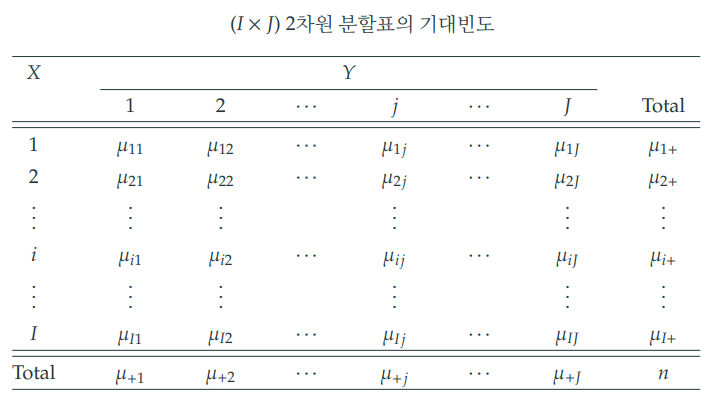
1-3. 귀무가설 하에서 기대빈도의 추정량
이때 이고 일 때의 확률 ()는 모수이다.
이 모수를 추정하기 위한 추정량을 로 표기한다.

에 따라 관측빈도표가 주어지면, 기대빈도는 주변합으로 표현할 수 있다.
📌 증명
귀무가설 하에서 와 가 독립이므로
그림의 하늘색 하이라이트와 같이 에 대한 기대빈도는 로 계산할 수 있다.
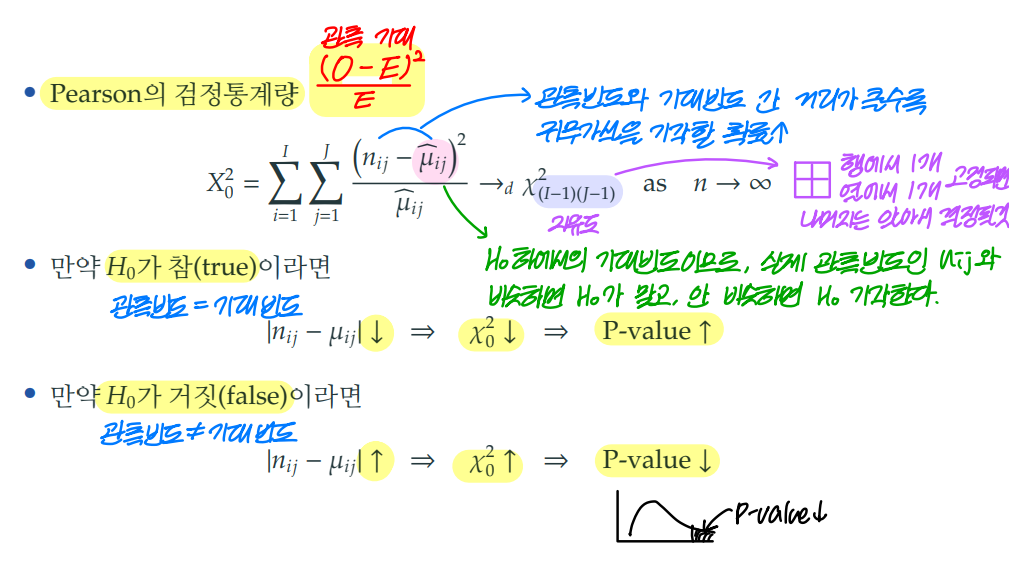
2. 피어슨의 카이제곱 검정 (pearson chi-square test)
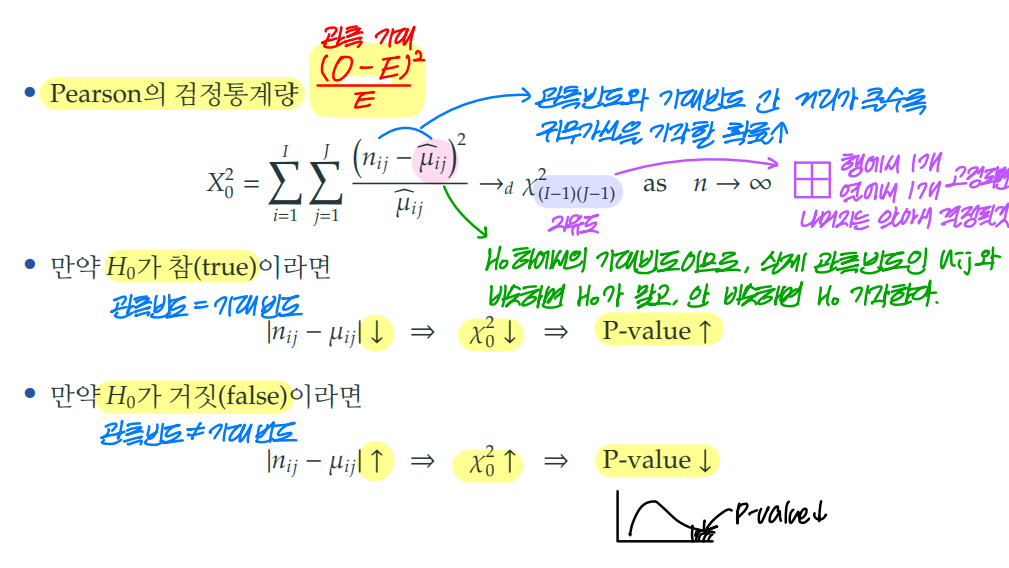
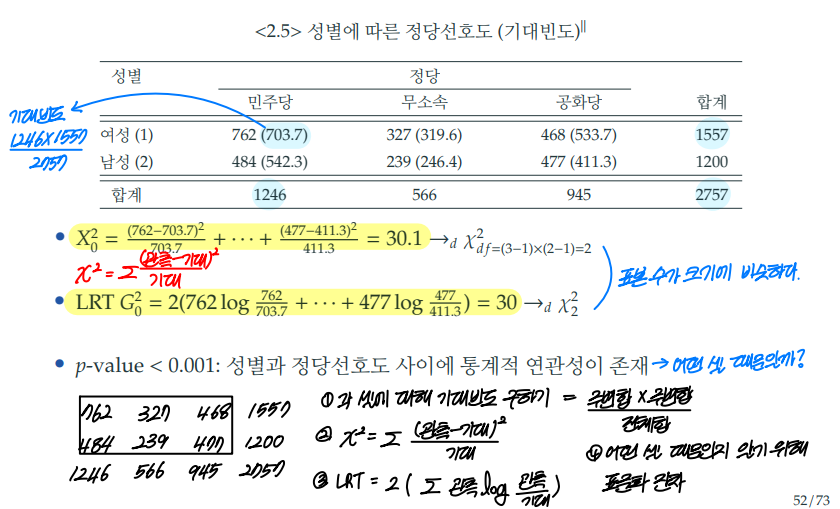
피어슨의 검정통계량 계산을 쉽게 표현하면 의 합이다.
계산식에 따라 계산된 카이제곱 검정통계량 값은 카이제곱 분포를 따르게 된다. 이때, 각 행과 열에서 1개의 값이 고정되면 나머지의 값은 전체 빈도에서 정해진 값을 빼는 방식으로 자동으로 정해진다.
따라서, 행과 열에서 각각 고정에 필요한 개수 1씩 빼고 이를 곱한 것이 자유도가 된다.
계산식에 따라 관측빈도와 기대빈도 간 거리가 클수록 카이제곱 검정통계량 값이 커진다.
카이제곱 검정통계량 값이 커지면 p-value 값은 작아지며, 관측빈도와 기대빈도가 같다는 귀무가설을 기각할 확률이 커진다.
카이제곱 독립성 검정 요약
- 카이제곱 통계량, 가능도비 통계량 모두 대표본을 전제로 한다. () 즉, 최소한 셀의 조합보다 표본이 클 때 잘 동작한다.
- 카이제곱 독립성 검정을 위한 최적의 조건은 "모든 셀 값이 최소한 5 이상" 이어야 한다.
- 어떤 셀의 기대빈도가 5보다 작을 경우, 근사분포가 아닌 정확검정 (exact test) 을 실시하는 것이 좋다. 정확검정은 다음 포스트에서 자세히 서술한다.
3. 가능도비 검정 (LRT; liklihood-ratio test of independence)

LRT 검정통계량은 로 계산된다.
이때 로그함수 속의 나눗셈은 와 같이 빼기로 표현할 수 있다.
즉, LRT 검정통계량도 카이제곱 검정통계량과 마찬가지로 관측빈도와 기대빈도 사이의 차이를 계산하는 통계량이다.
관측빈도와 기대빈도 사이의 차이 ↔️ LRT 검정통계량 ↔️ p-value 간 관계는 위와 같다.
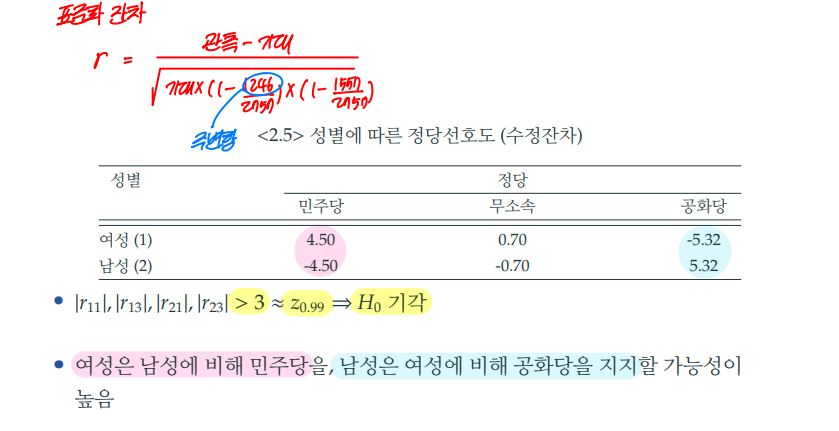
4. 표준화 잔차 (standardized residual)
앞의 두 통계량은 독립인지 아닌지 검정했다면, 표준화 잔차는 특히 어떤 셀로 인해 독립성이 깨졌는지 확인할 수 있는 지표이다.

5. 1~4번에 대한 R 실습
- 데이터 준비
Party <- matrix(c(762,484,327,239,468,477), nrow = 2)
dimnames(Party) <- list("Gender" = c("Female","Male"),
"Party" = c("Dem","Ind","Rep"))
Party
## Party
## Gender Dem Ind Rep
## Female 762 327 468
## Male 484 239 477- 피어슨의 카이제곱 검정
(res3 <- chisq.test(Party, correct = FALSE))
## Pearson's Chi-squared test
##
## data: Party
## X-squared = 30.07, df = 2, p-value = 2.954e-07- 기대빈도 출력
res3$expected
## Party
## Gender Dem Ind Rep
## Female 703.6714 319.6453 533.6834
## Male 542.3286 246.3547 411.3166
res3$p.value # p-value
## [1] 2.953589e-07- 표준화 잔차 출력
res3$stdres
## Party
## Gender Dem Ind Rep
## Female 4.502054 0.6994517 -5.315946
## Male -4.502054 -0.6994517 5.315946- 가능도비 검정
library(MASS)
(res4 <- loglm(formula = ~ Gender + Party, data = Party))
## Call:
## loglm(formula = ~Gender + Party, data = Party)
##
## Statistics:
## Xˆ2 df P(> Xˆ2)
## Likelihood Ratio 30.01669 2 3.033598e-07
## Pearson 30.07015 2 2.953589e-076. 순서자료에 대한 독립성 검정
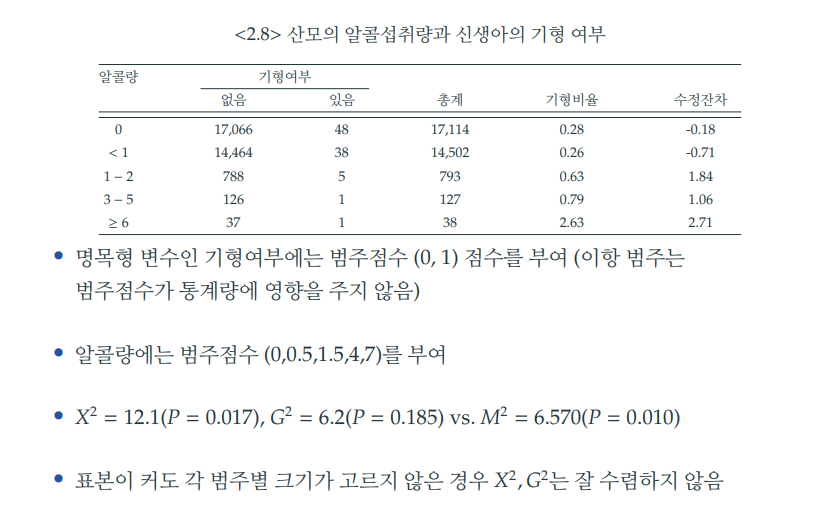
피어슨, 가능도비 검정의 한계
- 두 변수 모두 명목명으로 취급한다.
- 그러나, 순서형 자료 또한 범주형 자료에서 자주 관측된다. (ex:연령대, 성적등급 등)
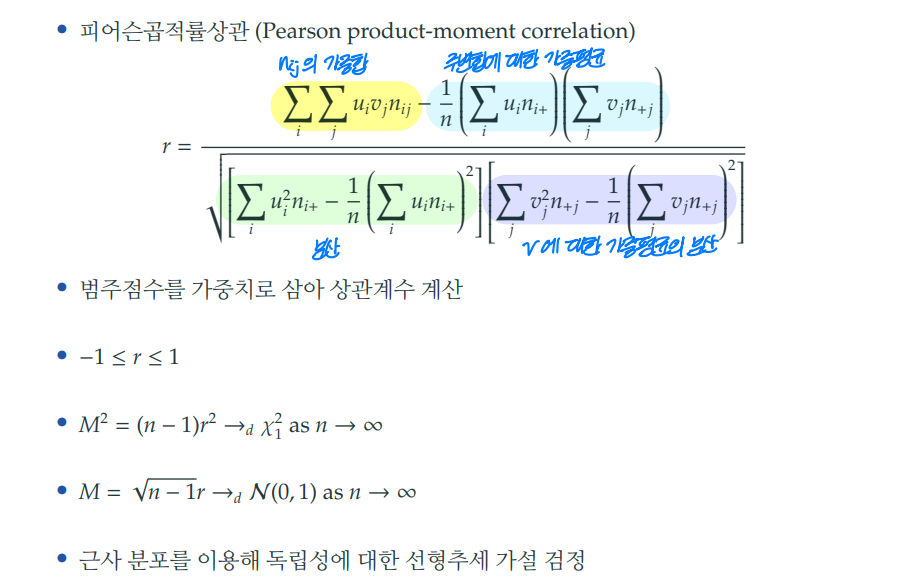
- 범주에 점수를 부여해 가중평균을 활용한 선형추세 (linear trend)를 볼 수 있다.
6-1. 피어슨 곱적률상관 (pearson product-moment correlation)
6-2. R 실습
- 데이터 준비
alc <- c(0, 0.5, 1.5, 4, 7)
def <- c(0, 1)
temp <- expand.grid(alc = alc, def = def)
ct <- c(17066,14464,788,126,37,48,38,5,1,1)
temp <- cbind(temp, count = ct)
(tab <- xtabs(ct ~ alc + def, data = temp))
## def
## alc 0 1
## 0 17066 48
## 0.5 14464 38
## 1.5 788 5
## 4 126 1
## 7 37 1- 피어슨, 가능도비 검정
loglm(formula = ~ alc + def, data = tab)
## Call:
## loglm(formula = ~alc + def, data = tab)
##
## Statistics:
## Xˆ2 df P(> Xˆ2)
## Likelihood Ratio 6.201998 4 0.1845623
## Pearson 12.082055 4 0.0167514- 피어슨 곱적률상관분석
res <- apply(temp[,1:2], 2, function(x) rep(x, temp$count))
(M2 = cor(res[,1], res[,2])ˆ2*(nrow(res)-1))
## [1] 6.569932
pchisq(M2, df = 1, lower.tail = FALSE)
## [1] 0.01037159
(res6 <- cor.test(res[,1], res[,2],
alternative="two.sided",method="pearson"))
##
## Pearson's product-moment correlation
##
## data: res[, 1] and res[, 2]
## t = 2.5634, df = 32572, p-value = 0.01037
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.003342942 0.025057844
## sample estimates:
## cor
## 0.01420207
res6$statisticˆ2; M2
## t
## 6.571056
## [1] 6.5699327. 소표본에 대한 정확검정
7-1. 초기하 분포 (hypergeometric distribution)
초기하 분포는 N개 중 K개를 비복원 추출 시 원하는 M개 중 x개가 관측될 확률에 관한 분포이다.
- M : 성공의 개수
- N-M : 실패의 개수

초기하 분포에서 샘플링하는 과정은 다음과 같다.
1. N개 중 K개를 추출한다. ex) 7개 중 2개를 추출한다.
2. M개 중 x개 추출을 원한다. ex) 3개 중 1개 추출을 원한다.
3. 나머지 N-M개 중 K-x개를 추출한다. ex) 나머지 7-3 = 4개 중 2-1 = 1개를 추출한다.

7-2. Fisher 2x2 표를 위한 정확검정
피셔의 정확검정은 다음과 같은 특징을 갖는다.
- 설명변수와 반응변수를 구분하지 않기 때문에 전향적 및 후향적 연구 모두에 사용이 가능하다.
- 2x2 분할표가 아닌 분할표에서도 사용할 수 있으나 계산과정이 복잡하다.
- 소표본이므로 다소 보수적인 검정방법이다.
1) 초기하분포 가정

행 및 열의 합이 고정되었다고 가정한다.
즉, 주변합이 고정되었을 때, 각 셀에 대한 확률은 초기하분포를 따르게 된다.
2) 귀무가설 정의

정확검정을 위한 귀무가설은
- 양측 검정 : 오즈비가 1이다. vs 오즈비가 1이 아니다.
- 단측 검정 : 오즈비가 1이다. vs 오즈비가 1보다 크다 or 작다.
로 정의한다.
3) 피셔의 차 맛보기 실험 R 실습
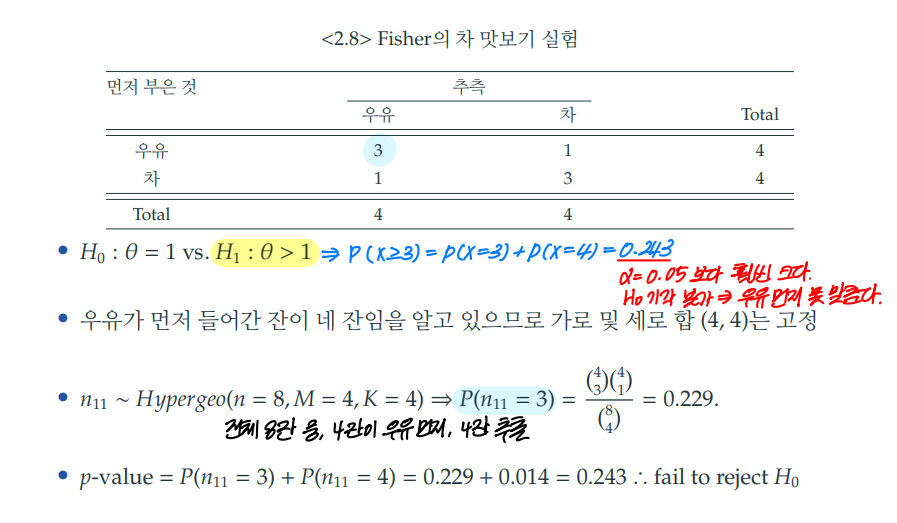
tea <- matrix(c(3,1,1,3), nrow = 2)
dimnames(tea) <- list("Add" = c("Cond.milk","Tea"),
"Pred" = c("Cond.milk","Tea"))
tea
## Pred
## Add Cond.milk Tea
## Cond.milk 3 1
## Tea 1 3
(rslt6 <- fisher.test(tea, alternative = "greater"))
##
## Fisher's Exact Test for Count Data
##
## data: tea
## p-value = 0.2429
## alternative hypothesis: true odds ratio is greater than 1
## 95 percent confidence interval:
## 0.3135693 Inf
## sample estimates:
## odds ratio
## 6.408309💡 질문과 피드백은 댓글에 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.
