1. 비율의 차이

1-1. 개요

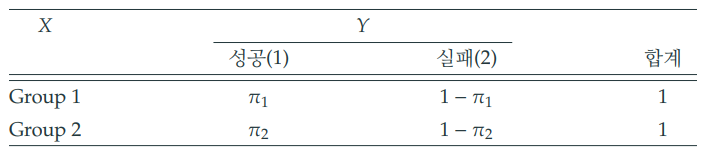
• 두 그룹에서 독립적으로 사건들을 관측하면,

  • 그룹 1에서 Y에 대한 조건부 분포는 베르누이 분포를 따른다.
    $Y|X=1\sim B(n_1, \pi_1)$
  • 그룹 2에서 Y에 대한 조건부 분포는 베르누이 분포를 따른다.
    $Y|X=1\sim B(n_2, \pi_2)$

• $\pi_1-\pi_2$ 는 그룹 1과 그룹 2 간 성공 확률의 차이를 의미한다. 이를 우리가 추정하고자 하는 모수로 정의하자.

• $\widehat{\pi_1-\pi_2}$ 는 모수에 대한 추정량이다.

• 모수에 대한 추정량은 개별 추정량의 차이로 정의할 수 있다. 따라서, 다음이 성립한다. $\widehat{\pi_1-\pi_2} = \hat\pi_1 - \hat\pi_2 = p_1 - p_2$

1-2. $p_1 - p_2$의 표준오차 추정

1-3. $\pi_1 - \pi_2$의 $100(1-\alpha)$ 신뢰구간

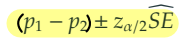
1-4. $H_0:\pi_1=\pi_2$ 검정을 위한 검정통계량

1-5. 예시 : 아스피린 복용과 심근경색 발병

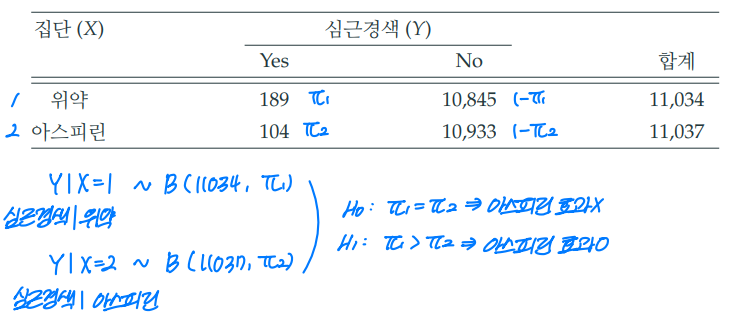아스피린 복용과 심근경색의 발병관계 규명을 위한 성인 남성 약 22,000명을 대상으로 대규모 무작위 임상시험을 진행했다.

1) 각 그룹에서 성공 확률$(p_1, p_2)$을 계산한다.

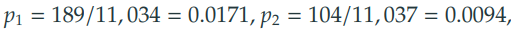
2) 전체에서 성공 확률인 "공통표본비율"을 계산한다.

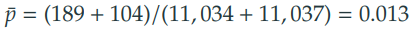
3) 공통표본비율의 표준오차$(SE)$를 계산한다. 표준오차는 추정된 비율 $p$의 변동성을 측정한다.

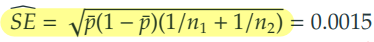
4) 위약 집단과 아스피린 집단의 모비율 차이에 대한 95% 신뢰구간을 구한다.

95% 신뢰구간이 항상 양수이다.
$(\pi_1-\pi_2)$에 대한 신뢰구간 $>0 \rightarrow \pi_1 > \pi_2$
이는 위약을 복용했을 때 심장병 발병확률이 아스피린을 복용했을 때 심장병 발병 확률보다 크다는 것을 의미한다.
즉, 아스피린이 심근경색 발병을 줄이는데 유의미한 효과가 있으므로 귀무가설 $H_0$을 기각한다.

---

2. 상대위험도 (RR; relative risk)

2-1. 개요

• 2-1의 "비율의 차이"는 차이의 크기만 파악할 수 있다.
• 예를 들어, 두 값의 차이는 0.009로 동일하지만,
  • $0.010-0.001 = 0.009
  • $0.410-0.401 = 0.009
• 비율의 관점에서는 차이가 큰 것을 볼 수 있다.
  • $0.010/0.001 = 10$
  • $0.410/0.401 = 1.023$

단순한 값의 차이보다 비율이 정보전달에 더 효율적일 수 있다.
특히 0~1사이의 값일 때, 비율로 계산하는 것이 좋다.
이 관점에서 만들어진 개념이 "상대위험도"이다.

2-2. 정의

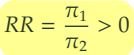
• $RR<1 \Leftrightarrow \pi_1<\pi_2$ : 위약 복용후 심근경색 발병 확률 < 아스피린 복용 후 심근경색 발병확률
• $RR=1 \Leftrightarrow \pi_1=\pi_2$ : 위약 복용후 심근경색 발병 확률 = 아스피린 복용 후 심근경색 발병확률
  • 이는 위약/아스피린 복용과 심근경색 발병 간 독립이라는 것을 의미한다.
• $RR>1 \Leftrightarrow \pi_1>\pi_2$ : 위약 복용후 심근경색 발병 확률 > 아스피린 복용 후 심근경색 발병확률

2-3. 추론 개요

• $\widehat{RR} > 0$의 분포는 highly right skewed 형태이다. 즉, 오른쪽으로 봉우리가 치우쳐진 형태이다.
• 일반적으로 통계적 추론은 정규분포를 가정하기 때문에, 오른쪽으로 봉우리가 치우쳐진 분포 형태를 정규분포와 유사하게 변환해주어야 한다.
• 이때, "로그 변환"이 이를 해결해 줄 수 있다. 로그 변환된 상대 위험도를 "로그-상대위험도"라고 정의한다.

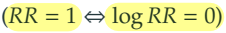
델타 메소드 (delta method)

• 상대위험도의 추론을 위해 델타 메소드를 사용할 것이다. 델타 메소드란 어떤 분포가 정규분포를 따른다면, 어떤 분포에 함수를 씌운 분포도 정규분포를 따른다는 정의이다.

• 이때, 로그 함수를 씌운다면, 분포의 형태는 다음과 같다.

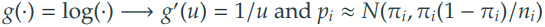
✅ 정리
1. 두 성공확률의 효과적인 비교를 위해 "상대위험도" 개념을 사용한다.
2. 상대위험도는 오른쪽으로 봉우리가 치우쳐진 분포를 갖는다.
3. 추론을 위해서는 정규분포 형태여야 한다.
4. 따라서, 상대위험도 분포를 정규분포 형태로 변환하여, 상대위험도 값을 추론할 것이다.
5. 이때, 로그 함수를 씌우면 정규분포 형태로 변환할 수 있고, 이를 "로그-상대위험도"라고 정의한다.

1) 로그-상대위험도 ($\log{\widehat{RR}}$) 의 기대값 추론

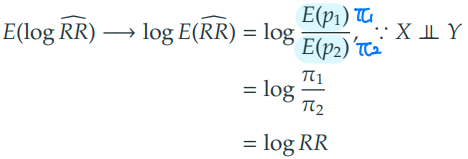
cf)$E(\log{\widehat{RR}})=\log{RR}$ 이므로, 불편추정량의 정의를 만족한다.

2) 로그-상대위험도 ($\log{\widehat{RR}}$) 의 분산 추론

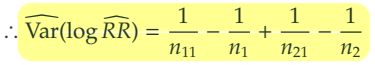증명

3) 로그-상대위험도 ($\log{\widehat{RR}}$) 의 신뢰구간 추론

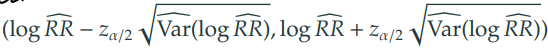
4) 상대위험도 ($RR$) 의 신뢰구간은 "로그-상대위험도 ($\log{\widehat{RR}}$) 의 신뢰구간"에 $exp$ 변환을 하면 된다.

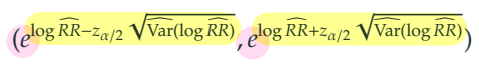
5) 예제

1. 위약, 아스피린 그룹별 심근경색 발병 확률 계산

• $p_1 = {189 \over 11034} = 0.0171$
• $p_2 = {104 \over 10933} = 0.0094$

2. 심근경색 발병에 대한 상대위험도 $(\widehat{RR})$ 계산

$(\widehat{RR}) = {p_1\over p_2} = {0.0171\over0.0094} = 1.82$

• 위약 집단이 아스피린 집단에 비해 심근경색 비율이 82% 더 높다.
• cf) 비율의 차이 관점 : $p_1, p_2$의 차이는 $0.008$로 비율의 차이는 정보전달에 효과적이지 않다. 반면에, 위의 상대위험도는 정보전달에 효과적이다.

3. 상대위험도 $(\widehat{RR})$에 대한 95% 신뢰구간 계산

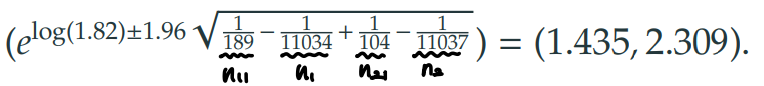
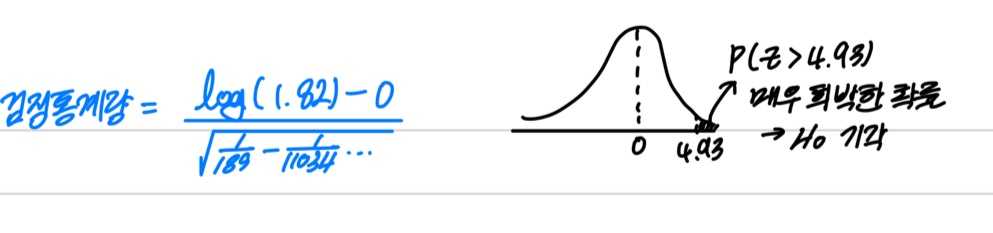
4. $H_0 : \log{RR} = 0$에 대한 검정통계량 계산

$H_0 : \log{RR} = 0 \rightarrow Z_0 = 4.9301$
4.9301 이라는 검정통계량 값에 대한 p-value는 0.001보다 작으므로, $H_0$을 기각한다.

---

3. 전향적 연구, 후향적 연구

3-1. 전향적 연구 (prospective study)

1) 개념

• 표본 수집 전, 설명변수의 표본수&모집방법 등의 계획에 따라 일정 시간 이후 반응을 관찰한다. ex) 임상실험
• 그룹 간 직접적인 조건부확률 비교가 가능하다.
  
  
  

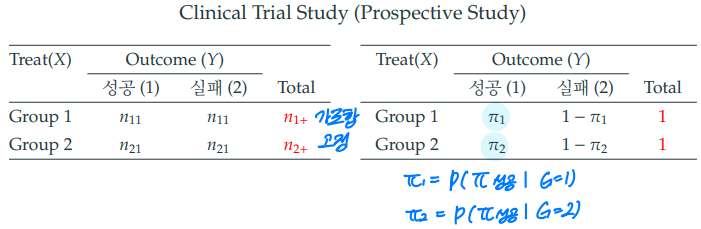
2) 실험 연구 (experimental study)

• 실험자가 변수를 통제하여 다른 변수에 미치는 영향을 분석한다.
• 실험 그룹 내 표본은 동일한 특성을 가져야 한다. (나이, 혈압, 건강상태 등)
• 대부분의 임상시험이 해당된다.
• 실험그룹(X)을 실험자가 임의로 선택한다.
• 랜덤화가 되지 않는다는 문제점이 있다. 예를 들어, A그룹에 40대가 1명이라면, B그룹에도 40대를 1명 배정해야 한다.
• 윤리적인 문제점이 존재한다. 예를 들어, 임상실험 연구에서 환자는 신약을 복용하고 싶지만, 기존약 또는 위약을 복용하는 그룹에 할당될 수 있다.

3) 코호트 연구 (추적연구, cohort study)

• 피실험자가 실험그룹을 선택한 뒤 미래에 반응을 관찰한다. 예를 들어, 흡연 그룹 또는 비흡연 그룹을 선택한 뒤, 미래에 폐암 또는 정상 상태를 관찰한다.
• 역학 (epidemiology) 연구에 주로 활용된다.
• 피실험자를 통제하지 않는 관측연구 (observational study)이다.

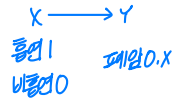
✅ 실험 연구 vs 코호트 연구

• 공통점 : 표본을 미리 정한다.
• 차이점 : 실험 연구는 외부 요인을 통제하지만, 코호트 연구는 외부 요인을 통제하지 않는다.

3-2. 후향적 연구 (retrospective study)

1) 개념

• 반응이 희박한 경우 목표한 표본수까지 전향적으로 관측하는 것이 어렵다. 예를 들어, 흡연자 500명 중 폐암 환자가 1명이라면, 전향적 연구가 무의미해질 수 있다. 따라서, 폐암 환자를 500명 뽑고 과거에 흡연을 했는지 되돌아본다.
• 현재 시점에 반응이 관측된 표본(폐암 환자)의 과거를 살펴본다.
• 반응변수의 표본수(폐암 환자 500명)를 사전에 정한다.

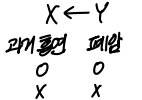
2) 사례-대조 연구 (case-control study)

• 현재 반응을 한 그룹(case 그룹)과 반응하지 않은 그룹(control 그룹)의 인원을 모아 그들의 과거가 어떤 실험그룹에 해당하는지 살펴본다.

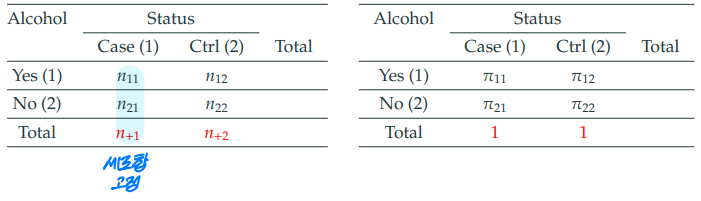
⭐ 후향적 연구에서는 "비율의 차이 & 상대위험도" 개념을 활용할 수 없다.

• 후향적 연구에서는 설명변수(실험그룹, X)이 통제되지 않았다.
• 즉, 비율의 차이 & 상대위험도는 가로합이 정해져 있어야 하지만
• 후향적 연구는 세로합에 대해서만 계산이 가능하다.

---

4. 오즈비 (OR; odds ratio)

4-1. 개념

• 성공 확률이 $\pi$인 경우 성공에 대한 오즈비는 다음과 같이 정의한다. 이때 최대우도추정법(MLE)에 의해 모수 $\pi$를 추정량 $p$를 사용해 추정할 수 있다.

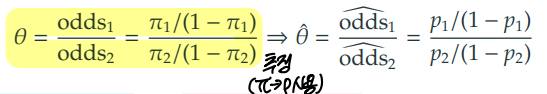
• 이차원 분할표에서 오즈와 오즈비는 다음과 같이 계산된다.

• "성공 확률에 대한 오즈비가 3이다."의 의미 : 성공오즈/실패오즈로 계산되는 오즈비가 3이며, 이는 성공 확률이 실패 확률의 3배라는 것을 의미한다.

• 오즈비는 전향적 연구, 후향적 연구에서 모두 사용할 수 있는 연관성 측도이다.

• 행과 열이 바뀌어도 오즈비 계산에 영향을 주지 않기 때문에, 오즈비에 대한 해석은 바뀌지 않는다.

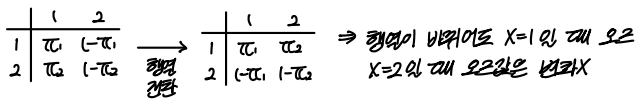
📌 상대위험도(RR) vs 오즈비(OR)

4-2. 예제

• 위약그룹의 오즈 ($\widehat{odds_1}$) 계산

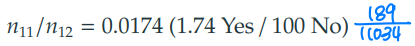
• 투약그룹의 오즈 ($\widehat{odds_2}$) 계산

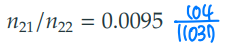
• 심근경색 발병 확률에 대한 오즈비 ($\hat\theta$) 계산

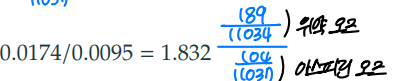
⭐ 오즈비(1.832)의 해석

• 위약을 복용한 그룹의 오즈가 아스피린을 복용한 그룹의 오즈보다 1.832배이다.
• 위약을 복용한 그룹의 오즈가 83.2% 높다.

4-3. 오즈비의 계산법 (cross-product)

이차원 분할표에서 오즈비는 cross-product 계산법을 통해 손쉽게 계산할 수 있다.

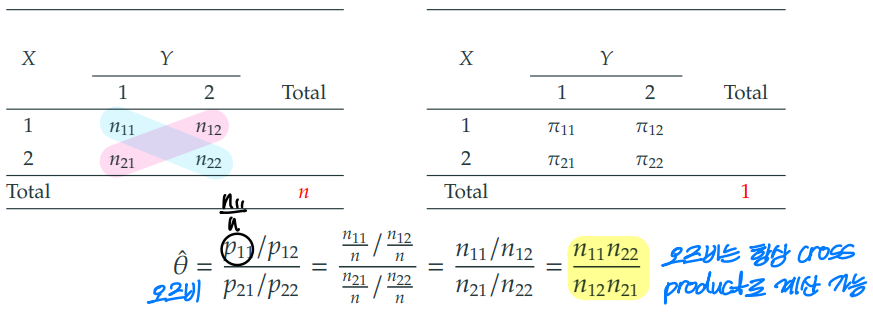
cf) 만약 특정 셀이 0인 경우, 각 셀에 0.5를 더하여 보정한 값으로 오즈비를 계산할 수 있다.

4-4. 오즈비의 추론

1) 로그-오즈비 ($\log{\hat\theta}$) 의 기댓값 추론

$\log{\hat\theta}$의 분포는 정규분포를 따른다.
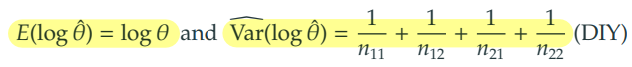증명

2) 로그-오즈비 ($\log{\hat\theta}$) 의 신뢰구간 추론

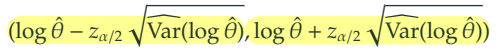
3) 오즈비 ($\hat\theta$) 의 신뢰구간 추론

---

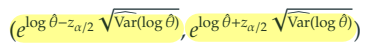
5. 상대위험도(RR) & 오즈비(OR)의 관계

• 위의 아스피린 복용에 따른 심근경색 발병 예제의 경우, 오즈비 1.832, 상대위험도 1.82로 유사한 것을 볼 수 있다.
• 따라서, 오즈비를 상대위험도처럼 해석할 수 있다.
  
  

⭐ 오즈비(OR)을 상대위험도(RR)처럼 해석할 수 있다.

• 상대위험도를 계산할 수 없는 자료에 대해 오즈비를 근사값으로 사용할 수 있다. at) case-control study
• 오즈비는 해석이 어렵기 때문에 상대위험도처럼 해석해서 직관적인 이해를 도울 수 있다.

5-1. 예제

1) 오즈비 계산

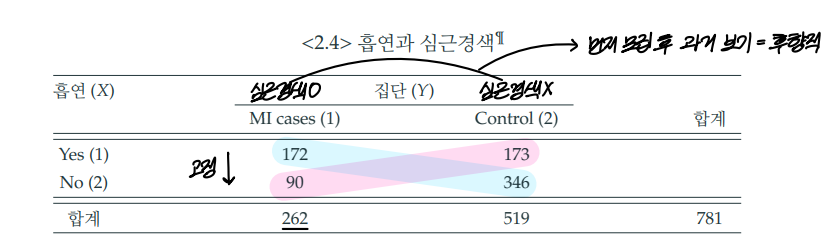
• 심근경색 환자 262명을 모집 후, 각 환자 당 두명의 환자를 대조군에 매칭했다.
• 심근경색 환자(Y)를 262명으로 모집했다는 것은 후향적 연구라는 것을 의미한다.
• 상대위험도는 반응변수(X)를 고정했을 때 계산이 가능하다. 후향적 연구는 상대위험도의 계산이 불가능하다.
• 따라서, 오즈비를 계산하고 이를 상대위험도와 유사하다고 가정하고 상대위험도처럼 해석한다.

2) 로그-오즈비 ($\log{\hat\theta}$) 의 신뢰구간 추론

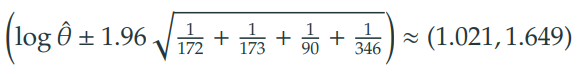
3) 오즈비 ($\hat\theta$) 의 신뢰구간 추론

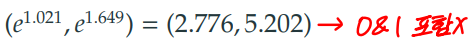
95% 신뢰수준에서 신뢰구간 (2.776, 5.202)의 해석
➡️ 흡연자의 심근경색 오즈는 비흡연자의 심근경색 오즈에 비해 2.7배에서 5.2배 더 크다.

4) 오즈비를 상대위험도로 해석

만약 $P(Y=1|X)$가 작다고 가정할 수 있다면 오즈비를 상대위험도에 근사해 해석할 수 있다.
예를 들어, 심근경색 비율$P(Y=1|X)$은 낮은 것으로 알려져있다.
이 경우, 오즈비의 추정량을 상대위험도 개념으로 근사적으로 해석할 수 있다.

---

6. R실습

• 데이터 준비

MI <- matrix(c(189, 104, 10845, 10933), nrow = 2)
dimnames(MI) <- list("Group" = c("Placebo","Aspirin"), "MI" = c("Yes","No"))

MI

## MI
## Group Yes No
## Placebo 189 10845
## Aspirin 104 10933

• 집단별 비율 확인

prop.table(MI, margin = 1) # margin: 1; row, 2; column

## MI
## Group Yes No
## Placebo 0.01712887 0.9828711
## Aspirin 0.00942285 0.9905771

• 비율의 차이 검정

prop.test(MI) # matrix: 2 columns, success and failure

## 2-sample test for equality of proportions with continuity correctio##

## data: MI
## X-squared = 24.429, df = 1, p-value = 7.71e-07
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## 0.004597134 0.010814914
## sample estimates:
## prop 1 prop 2
## 0.01712887 0.00942285
# help(prop.test)

• 상대위험도 ($RR$) 계산

prop.out <- prop.table(MI, margin = 1)
prop.out[1,1] / prop.out[2,1]

## [1] 1.817802

library(epitools)
res1 <- riskratio(MI, rev = "both", method = "wald")
res1$measure

## risk ratio with 95% C.I.
## Group estimate lower upper
## Aspirin 1.000000 NA NA
## Placebo 1.817802 1.433031 2.305884

res1$p.value

## two-sided
## Group midp.exact fisher.exact chi.square
## Aspirin NA NA NA
## Placebo 4.989646e-07 5.032836e-07 5.691897e-07

1.817802 : 상대위험도
1.433031, 2.305884 : 신뢰구간

• 오즈비 계산

res2 <- oddsratio(MI, rev = "both", method = "wald")
res2$measure

## odds ratio with 95% C.I.
## Group estimate lower upper
## Aspirin 1.000000 NA NA
## Placebo 1.832054 1.440042 2.33078

res2$p.value

## two-sided
## Group midp.exact fisher.exact chi.square
## Aspirin NA NA NA
## Placebo 4.989646e-07 5.032836e-07 5.691897e-07

1.832054 : 오즈비
1.440042, 2.33078 : 신뢰구간

---

💡 질문과 피드백은 댓글에 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.