1. 2차원 분할표 (two-way contingency table)

• $(I\times J)$ 분할표 : I개의 X변수와 J개의 Y변수로 구성된다.
• 범주형 변수들의 관찰도수를 2차원으로 정리한 표
  • 칸(cell) : 범주형 변수들의 범주 조합으로 이루어진 결합
  • 관찰도수, 관찰빈도 : $n_{ij} = {cell frequency for (X = i,Y = j)}$
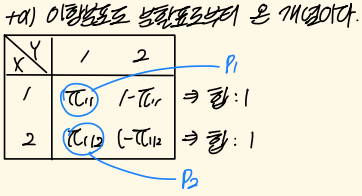
• 이항분포도 분할표로부터 온 개념이다.

1-1. 결합확률 (joint probability)

1) 정의

• $\pi_{ij} = P(X = i,Y = j) : (X,Y) = (i, j)$일 확률이다. 즉, X와 Y가 특정 값일 때 확률을 의미한다.
• $\pi_{i,j}$는 $(X,Y)$의 결합확률분포를 형성한다. 즉, 모든 i, j에 대해 확률의 합은 1이다.

2) 추정

---

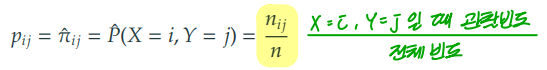
1-2. 주변확률 (marginal probability)

1) 정의

• 행(열)의 변수에 대한 주변분포 또는 주변합에 대한 분포를 의미한다.
• 결합확률의 행이나 열의 합에 대한 분포로 정의한다.

2) 추정

---

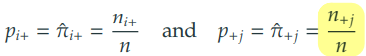
※ 실제 관측값의 관측빈도표

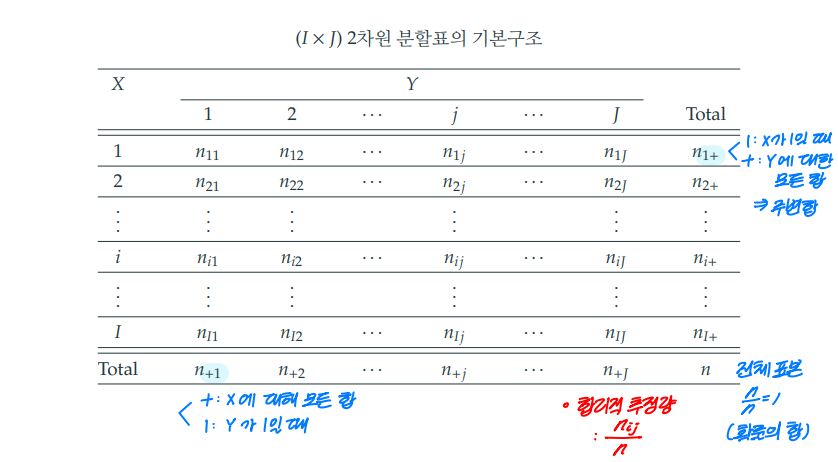
※ 결합확률과 주변확률표

cf) X의 수준별 혹은 Y의 수준별 관측도수를 통제하는 실험의 경우 추정할 수 없다.

---

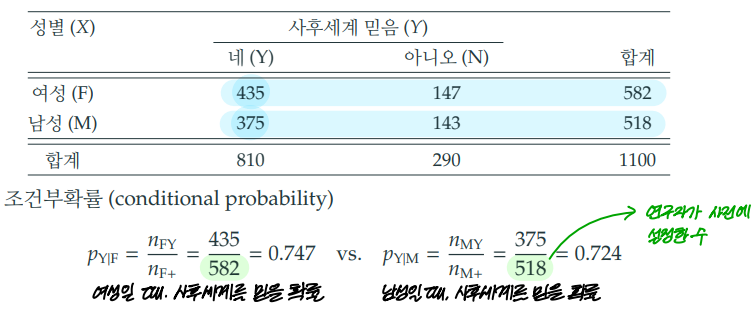
1-3. 조건부확률 (conditional probability)

1) 정의

확률을 계산하는 공간을 제약한다.

※ X를 고정했을 때, 조건부확률표

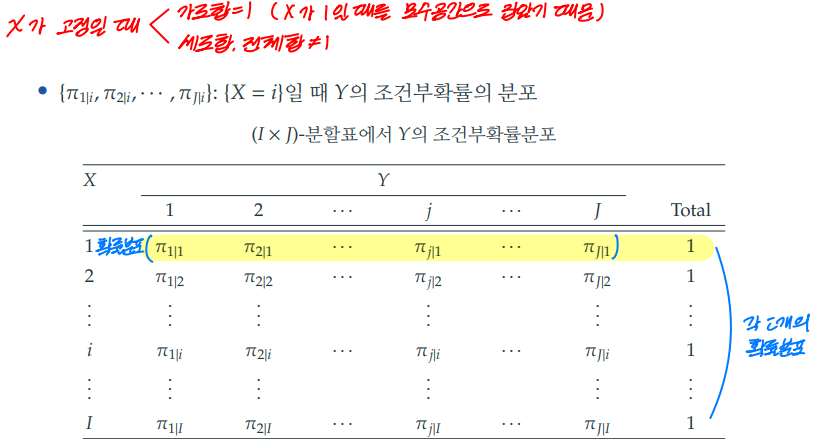
이때, 가로합이 1인 이유를 증명하면 다음과 같다.

※ Y를 고정했을 때, 조건부확률표

2) 추정

3) 예시

---

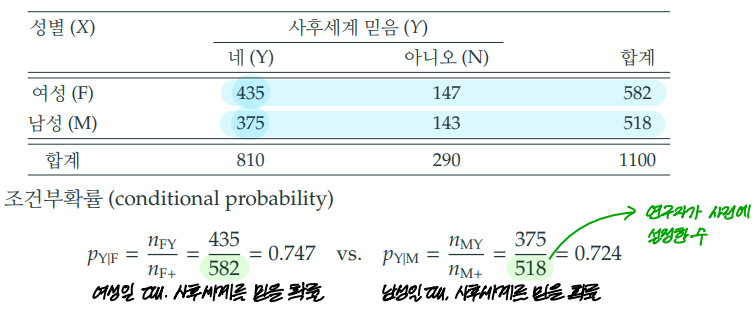
2. 통계적 독립성 (indendence)

• 두 사건 A,B가 독립일 때, 필요충분조건은 다음과 같다.

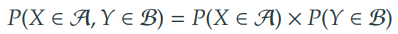
• 두 확률변수 X, Y가 독립일 때, 필요충분조건은 다음과 같다.

위와 같은 정의는 독립성 검정에 사용된다.

---

💡 질문과 피드백은 댓글에 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.