1. 변수의 종류

1-1. 변수의 특성에 따른 분류

1) 수치형 변수 (numerical variable)

• 수 자체가 의미를 갖는다.
• 종류
  • 이산형 변수 (discrete variable) : 값이 셀 수 있는 집합에 속한다. ex) 불량 제품의 수
  • 연속형 변수 (continuous variable) : 값이 특정 구간에 속한다. ex) 신장, 체중

2) 범주형 변수 (categorical variable)

• 수가 의미를 갖지 않는다.
• 종류
  • 명목형 변수 (nominal variable) : 자료의 순서가 없는 경우 ex) 거주지역, 종교
  • 순서형 변수 (ordinal variable) : 자료의 순서가 있는 경우 ex) 5점 척도, 질병의 진행단계
    
    

---

1-2. 변수의 쓰임에 따른 분류

1) 반응 (response), 종속 (dependent), 결과 (outcome) 변수

설명변수에 의해 관측값을 예측 또는 그 변동이 설명되는 변수

2) 설명 (explanatory), 독립 (independent), 예측 (predictor) 변수

반응변수의 관측값을 예측 또는 변동을 설명하는 변수

✅ 범주형 자료분석

• 반응변수가 범주형인 자료를 분석하는 것을 의미한다.
• 설명변수는 회귀분석 때와 마찬가지로 수치형, 범주형 모두 가능하다.
  
  

---

2. 범주형 변수의 분포

• 범주형 변수는 주로 이항 (binomial) 또는 포아송 (poisson) 분포를 따른다고 가정한다.

2-1. 이항 분포 (binomial distribution)

• 실험의 총 시행횟수(n) 중, 성공횟수(X)의 확률(P)를 설명하는 분포
• ex) 앞면이 나올 확률 0.5인 동전을 10번 던졌을 때 분포가 이항분포이다.
  
  

1) 확률변수, 확률질량함수

• 이항 분포는 성공확률이 0 또는 1인 n개의 독립적인 베르누이 시행이다.
  $\pi \in (0,1)$
• 이항 확률변수의 확률질량함수
  
  
  

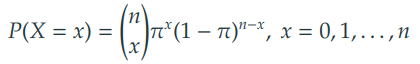
2) 기댓값, 분산

• 기댓값 (expectation)
  

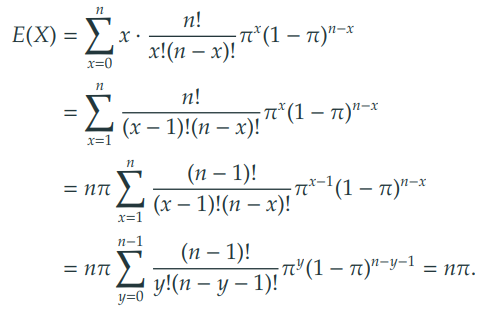
• 분산 (variance)
  
  
  

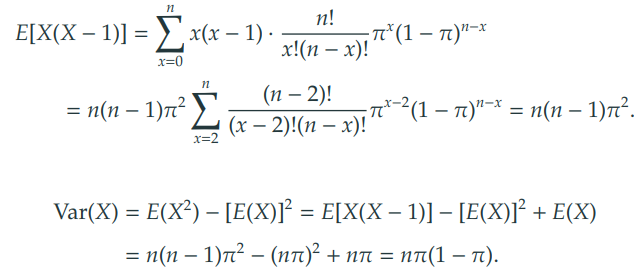
3) 특징

• 분산이 기댓값보다 작다
  

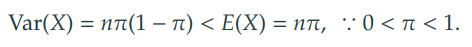
• 중심 극한 정리 (CLT)에 의해 다음이 성립한다.
  
  
  

---

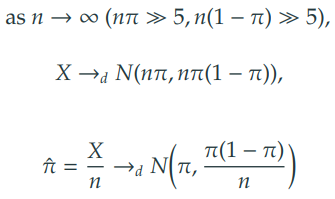
2-2. 포아송 분포 (poisson distribution)

• 일정 단위(시간 또는 공간) 내 발생횟수(X)의 기댓값($\mu$)을 설명하는 분포
• 즉, 이항 분포에서 시행횟수(n)는 매우 크고, 확률(P)는 매우 작을 때 사용할 수 있는 분포이다.
  
  

1) 포아송 확률변수, 확률질량함수

• 포아송 확률변수 $\mu$ : 단위 내 발생횟수의 기댓값
  • 일주일 동안 일어난 치명적인 교통사고 건수
  • 특정 병원에 내원하는 응급환자 수
  • 특정 생산라인에서 발생되는 불량품의 수
• 포아송 확률변수의 확률질량함수 $X~Pois(\mu)$
  
  
  

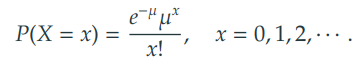
2) 기댓값, 분산

• 기댓값
  

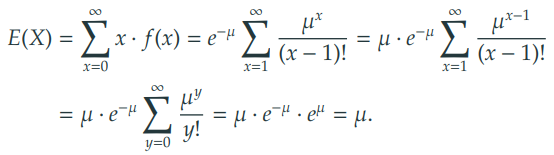
• 분산
  
  
  

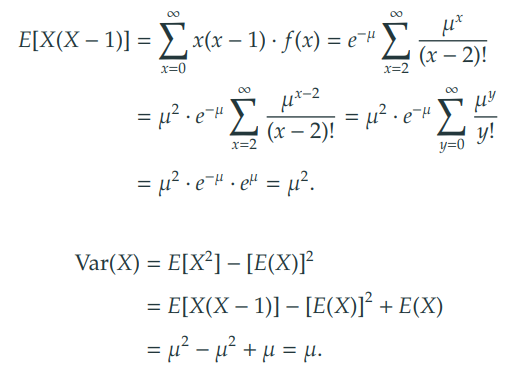
3) 특징

• 기댓값과 분산이 일치한다.
  

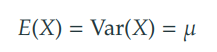
• 과대산포 (over-dispersion)의 경향을 갖는 데이터를 설명하기에는 지나치게 단순한 모형이다. 그럼에도 포아송 분포는 범주형 자료분석에서 유용하다.

  • 과대산포 데이터 : 관측도수의 평균보다 분산이 더 큰 데이터
    
    

---

3. 비율에 대한 추론

분포를 안다는 것은 모수에 대해 알고 있다는 것이다.
보통 분포는 유한한 파라미터를 갖는다.
예를 들어, 정규분포의 경우 평균과 분산이라는 2개의 파라미터를 알면 특정 값이 어떤 위치에 속하는지 알 수 있다.

3-1. 가능도 함수 (likelihood function)

관측된 자료가 주어졌을 때, 모수에 대한 함수로 표현한다.

3-2. 최대 가능도 추정량 (MLE; Maximum Likelihood Estimator)

• 가능도 함수는 관측된 표본이 주어졌을 때, 관심모수에 대한 함수이다.
• 가능도 함수를 최대화하는 값을 모수의 추정량으로 정의한다. 이것이 최대 가능도 추정이다.
• 가능도 함수에 $log$를 취한 로그-가능도 함수를 활용하면 곱셈을 덧셈으로 표현할 수 있기에 계산에 용이하다.
  

1) 이항 분포의 최대 가능도 추정량

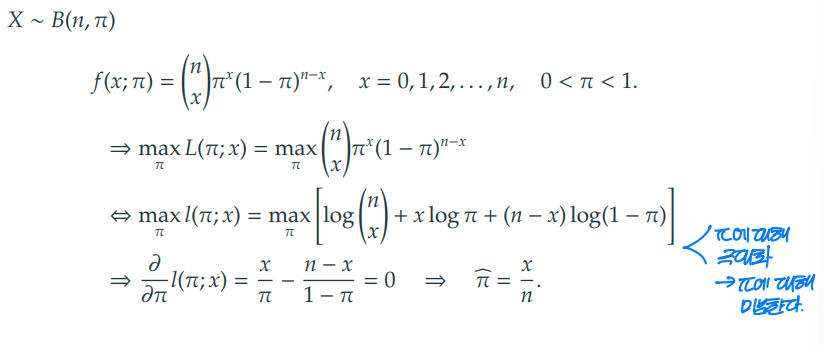
2) 포아송 분포의 최대 가능도 추정량

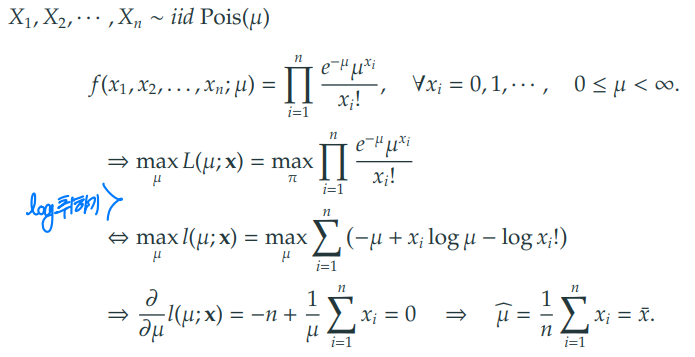
3-3. 비율에 대한 추론

1) 중심 극한 정리에 의한 정규 분포 근사

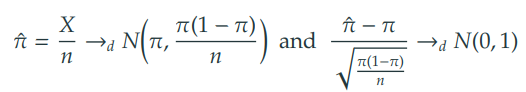
2) $H_0 : \pi = \pi_0$ 에서의 검정통계량

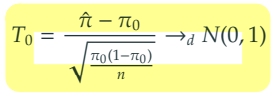
3) $\pi$에 대한 $(100-\alpha) \times 100$ 신뢰구간

---

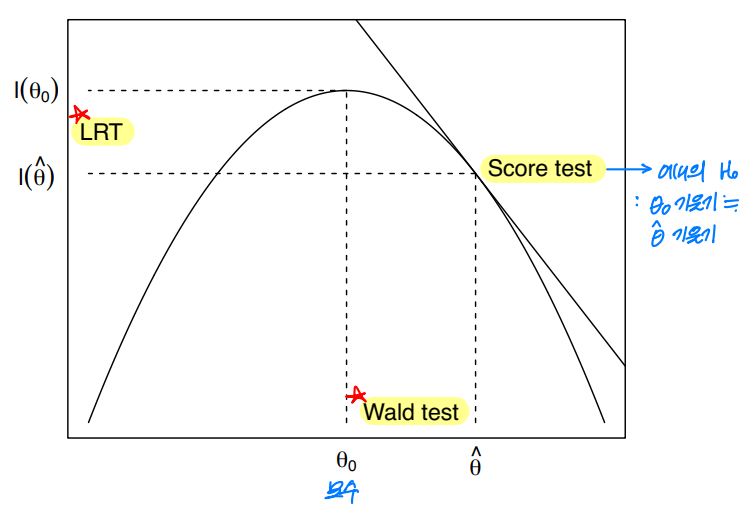
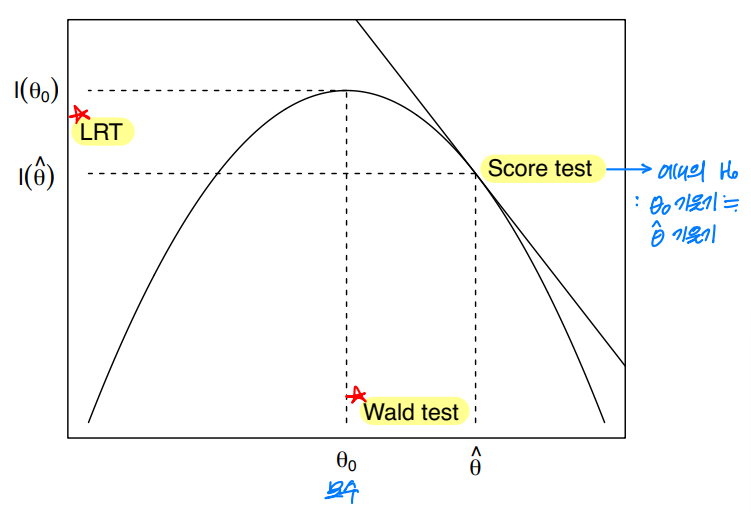
4. 검정의 세 가지 방법

4-1. Wald test

• $\theta$ : 관심모수, $\hat\theta$ : $\theta$의 추정량
• 중심 극한 정리에 의해 다음이 성립한다.
  
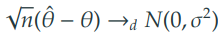
• $H_0 : \theta = \theta_0$ 하에서, 다음이 성립한다.
  
  
  

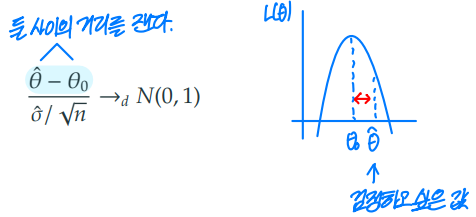
4-2. Score test

검정하고 싶은 $\hat\theta$의 기울기가 0에 가까운지 검정한다.

4-3. Likelihood ratio test

✅ 세 가지 검정법 비교

---

💡 질문과 피드백은 댓글에 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.