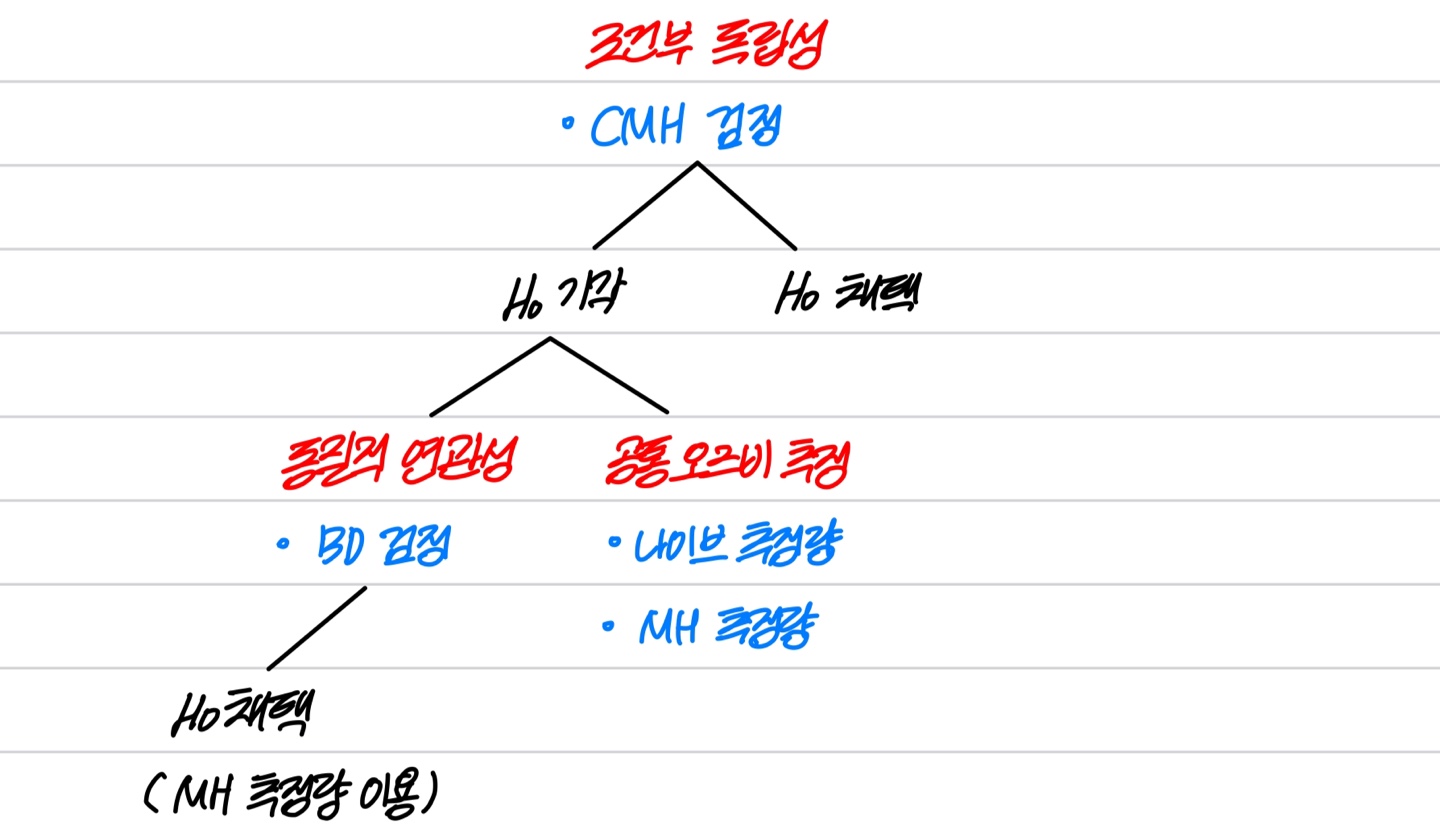
1. 조건부 독립성 (conditional independence)

cf) 동질적 연관성 (homogeneous association)

• $(X,Y,Z)$에 대한 $(2 \times 2 \times K)$ 분할표가 있을 때, 동질적 연관성은 Z 수준에 관계없이 오즈비가 동일한 것을 의미한다.
  $\theta_{XY(1)} = \theta_{XY(2)} = ... = \theta_{XY(K)}$
• X와 Y의 조건부 독립성은 동질적 연관성에서 모든 오즈비가 1로 동일한 경우를 의미하는 동질적 연관성의 한 케이스이다.
  $\theta_{XY(1)} = \theta_{XY(2)} = ... = \theta_{XY(K)} = 1$
• 모든 쌍의 변수들이 조건부 독립인 경우 동질적 연관성이 존재한다.
• 오즈비는 행 또는 열을 바꾸어도 동일한 "대칭성"을 갖는다. 즉, 교호작용이 없기 때문에 $XY$에 대해 동질적 연관성이 있을 경우 $XZ$와 $YZ$에도 모두 적용이 가능하다.
  
  

---

1-1. 코크란 멘텔 헨젤 (CMH; Cochran-Mantel-Haenszel) 조건부 독립성 검정

$2 \times 2 \times K$ 분할표의 조건부 독립성 검정에 CMH를 활용한다.

1) 귀무가설과 대립가설 정의

귀무가설은 조건부 독립을 가정한다. 즉, Z가 1~K일 때 모든 오즈비가 1로 동일하다는 것을 귀무가설로 정의한다.

대립가설은 최소 1개의 오즈비는 1이 아닐 것으로 정의한다.

2) 기댓값과 분산 계산

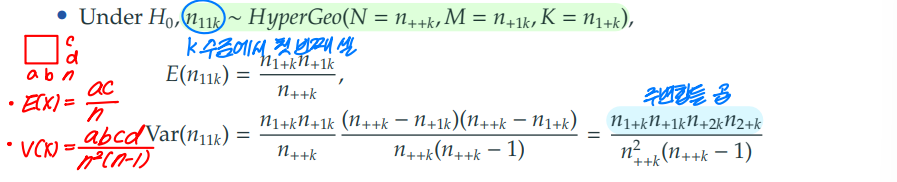
Z가 1~K일 때 모든 오즈비가 1로 동일하다는 귀무가설 하에서, 첫 번째 셀들은 초기하분포를 따른다.
좌측의 그림과 수식으로 기댓값과 분산의 계산 형태를 쉽게 이해할 수 있다.

3) CMH 검정통계량

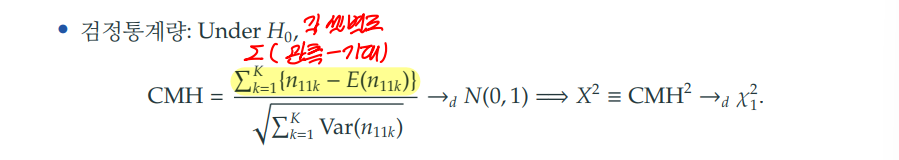
Z가 1~K일 때 모든 오즈비가 1로 동일하다는 귀무가설 하에서, CMH 검정통계량은 다음과 같이 계산된다.
이때, 분자는 각 셀별로 관측빈도에서 기대빈도를 뺀 값들의 합이다.
CMH 검정통계량은 표준정규분포를 따른다. 또한, 정규분포의 제곱이 카이제곱분포를 따른다는 법칙에 의해 $CMH^2$도 카이제곱 분포를 따른다.

✅ CMH 검정통계량 특징

• $n_{11k}-E(n_{11k})$의 부호가 모든 k에 대해 비슷하면 검정통계량이 증가한다. 즉, Z 수준에 따른 각 분할표의 첫 번째 셀의 값과 그 기댓값의 차이의 부호가 모든 분할표에 대해 비슷할 경우를 의미한다.
• 전체 표본수(n)이 크면 CMH 검정통계량은 정규 근사가 가능하다.
• 주변합 중 0인 부분이 있다면 해당 Z=k 분할표는는 CMH 통계량에 반영되지 않는다.
• 오즈비 개념을 사용하기 때문에 전향적, 후향적 연구에 모두 활용할 수 있다.

4) 예제

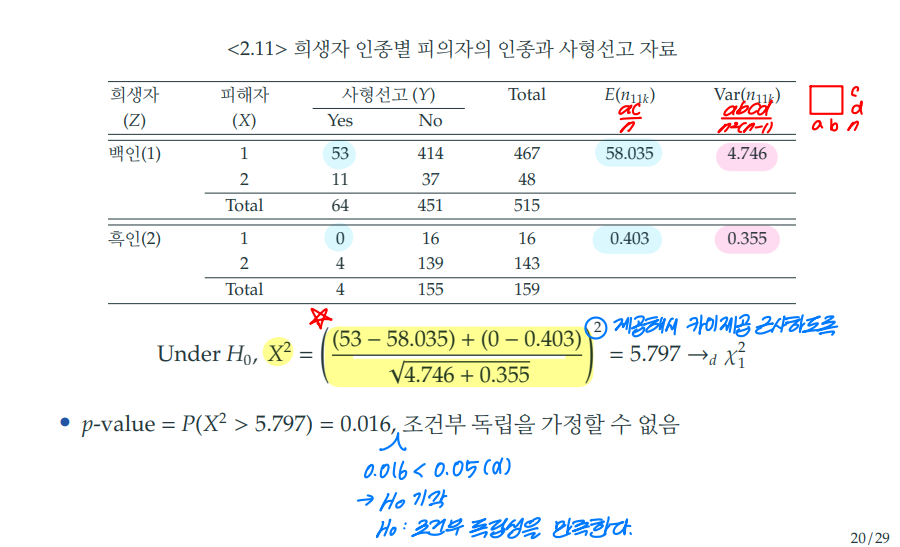
• 귀무가설 하에서 CMH 검정통계량은 5.797이다.
• 이에 대한 카이제곱 분포에서 p-value는 0.016이다.
• 0.016은 유의수준 0.01보다 크기 때문에, $H_0$을 기각한다.
  따라서, 희생자의 인종에 따른 오즈비는 Z수준에 따라 1로 동일하지 않다.
  즉, 조건부 독립성을 가정할 수 없다.
  
  

---

2. 공통 오즈비 (common odds ratio)

cf)

• 동질적 연관성 : Z가 1~K일 때, 모든 오즈비가 동일하다.
• 조건부 독립성 : Z가 1~K일 때, 모든 오즈비가 1로 동일하다.

앞에서 CMH 방법을 활용해 조건부 독립성에 대한 검정을 진행했다.
$(2 \times 2 \times K)$ 부분 분할표에서 모든 오즈비가 1로 동일하다는 조건부 독립성을 만족하지는 못하더라도 오즈비가 유사할 것으로 생각되는 경우 "공통 오즈비 추정" 을 시도해볼 수 있다.

2-1. 나이브 추정량 (Naive estimator)

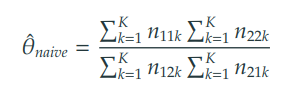
나이브 추정량은 부분 분할표 간 정보의 크기를 반영하지 못한다.

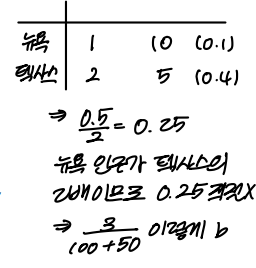
예를 들어, 뉴욕 인구가 텍사스의 2배이므로 0.25라는 추정값은 적절하지 못하다.
백인의 수에 추정값이 끌려갈 수 있기 때문이다.

---

2-2. 멘텔 헨젤 추정량 (MH; Mantel-Haenszel estimator)

부분 분할표 간 정보의 크기를 가중평균 개념을 활용해 보정한 추정량이다.

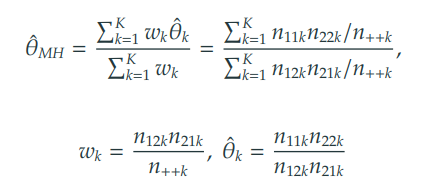
공통 오즈비 추정량을 일반적인 "평균"처럼 계산했을 때, 실제로는 가중치 $w$를 $1 \over 3$으로 사용한 경우이다.

---

2-3. 예제

피의자 인종과 사형 선고 예시에 대해 나이브 추정량과 멘텔 헨젤 추정량을 계산하면 다음과 같다.

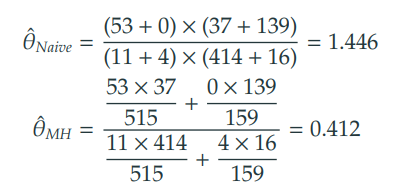
• 나이브 추정량 1.446 : 백인 피의자가 사형선고의 가능성이 더 높다.
• MH 추정량 0.412 : 흑인 피의자의 사형선고 가능성이 더 높다. (백인 오즈의 약 2.4배이다.)
  
  

이렇게 조건부 독립성을 만족하지 못하지만 유사한 오즈비를 가질 것으로 예상되는 분할표에 대해 공통 오즈비 즉, MH 추정량을 구했다.
이때, 동질적 연관성을 통계적 검정으로 가정할 수 있다면 MH 추정량의 활용도가 더 높다.

---

3. 동질적 연관성 (homogeneous association)

$(X,Y,Z)$에 대한 $(2 \times 2 \times K)$ 분할표가 있을 때, 동질적 연관성은 Z 수준에 관계없이 오즈비가 동일한 것을 의미한다.

모든 오즈비가 1로 동일하다는 조건부 독립성 검정에서 $H_0$을 기각했더라도 모든 오즈비가 동일하다는 조건만 검정하는 "동질적 연관성" 검정이 필요하다.
(동질적 연관성은 조건부 독립성의 완화된 조건이다.)

3-1. 브레슬로-데이 (BD; Breslow-Day) 동질적 연관성 검정

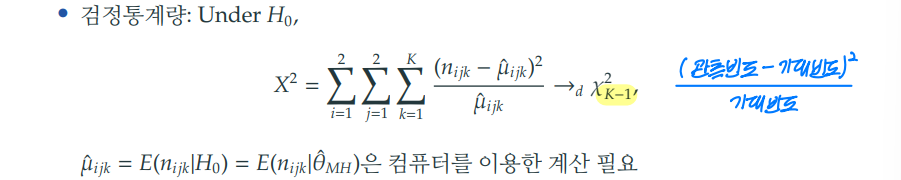
• 결과 해석 : $H_0$ (모든 오즈비 동일하다.)를 채택하면 위에서 보았던 공통 오즈비 추정량 ($\hat \theta_{MH}$는 좋은 추정량이 된다.

참고)

• 독립성에 대한 CMH 검정은 $(2이상 \times 2이상 \times K)$ 분할표로 일반화가 가능하다. 그러나 동질적 연관성에 대한 BD검정은 적용이 어렵다.
• 대체로 소표본에서 BD 검정 통계량은 CMH 검정 통계량보다 불안정한 검정력을 갖는다. 즉, BD 검정 통계량은 표본이 많아야 계산이 잘 된다.
  
  

---

4. R 실습

• 조건부 독립성 검정을 위한 CMH 검정 및 공통오즈비 추정

# conf.level = default is 0.95
cmh <- mantelhaen.test(penalty, correct = FALSE, conf.level = 0.95)
cmh # Reject H0

## Mantel-Haenszel chi-squared test without continuity correction
##
## data: penalty
## Mantel-Haenszel X-squared = 5.7959, df = 1, p-value = 0.01606
## alternative hypothesis: true common odds ratio is not equal to 1
## 95 percent confidence interval:
## 0.1991173 0.8519141
## sample estimates:
## common odds ratio
## 0.4118627

cmh$p.value
## [1] 0.01606399

cmh$estimate
## common odds ratio
## 0.4118627

cmh$conf.int
## [1] 0.1991173 0.8519141
## attr(,"conf.level")
## [1] 0.95

95% 신뢰구간에 따라 백인이 사형 선고를 받을 오즈비가 0.2~0.85 사이에 위치하고 1미만이므로, 흑인이 사형 선고를 받을 가능성이 더 크다는 것을 의미한다.

• 단측검정에서 멘텔 헨젤 공통 오즈비 추정

mantelhaen.test(penalty, correct = FALSE, alternative = "less")

## Mantel-Haenszel chi-squared test without continuity correction
##
## data: penalty
## Mantel-Haenszel X-squared = 5.7959, df = 1, p-value = 0.008032
## alternative hypothesis: true common odds ratio is less than 1
## 95 percent confidence interval:
## 0.0000000 0.7579643
## sample estimates:
## common odds ratio
## 0.4118627

• 동질적 연관성 검정을 위한 BD 검정

library(DescTools)
(bd <- BreslowDayTest(penalty))
##
## Breslow-Day test on Homogeneity of Odds Ratios
##
## data: penalty
## X-squared = 0.20376, df = 1, p-value = 0.6517
bd$p.value # 동질적 연관성 가정 가능
## [1] 0.6517023

df=1은 자유도를 의미하고 k=2이므로 2-1이 자유도가 된다.
p-value가 0.65로 유의수준보다 크기 때문에 대립가설을 기각한다. 즉, 모든 오즈비가 동일하다는 귀무가설을 기각하지 않게 되고, 동질적 연관성을 가정할 수 있게 된다.

---

💡 질문과 피드백은 댓글에 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.