
Computer Vision 관련 논문 리뷰를 하기 전, 꼭 알야야 하는 내용들을 정리해봤습니다 :) 가볍게 읽어 봐주세요~!
1. 컴퓨터 비전 Tasks
1.1 이미지 분류 (Image Classification)
: 미리 정해진 Category set에서 Input이미지가 어떤 클래스에 가장 가까운지 분류하는 문제
- Computer Vision의 핵심 Task
- 이미지 분류 모델은 정해진 Category Set 안에 있는 각 클래스들에 대한 Input 이미지의 분류 확률을 생성 -> 가장 확률이 높은 클래스로 최종 분류
📊 Evaluation metric:정확도(Accuracy)
👍 Input: 이미지
👎 Output: 클래스별 확률
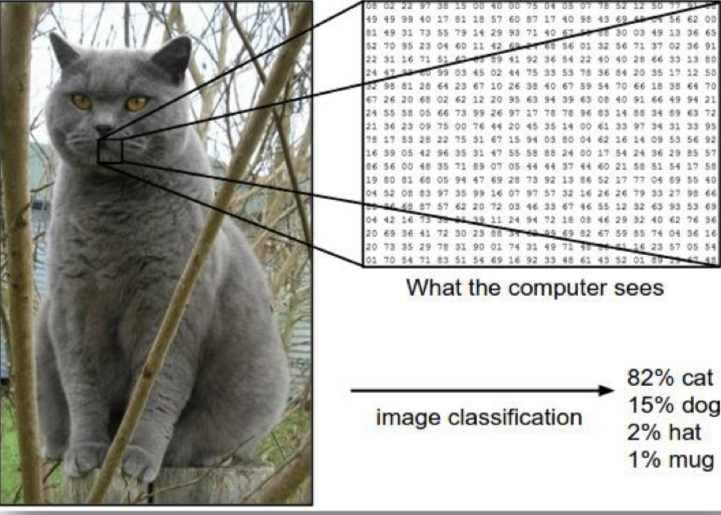
(출처: https://cs231n.github.io/classification/)
1.2 객체 위치 식별 (Object Localization)
: 전체 이미지에서 Main object의 Bounding Box를 찾아내는 문제
- Bounding Box란?
: 전체 이미지에서 object를 포함하고 있는 직사각형을 의미
- 1) (x,y,w,h)
: Box의 좌상단 꼭지점 x좌표, Box의 좌상단 꼭지점 y좌표, Box의 너비(Width), Bow의 높이(Height)
- (x1,y1,x2,y2)
: Box의 좌상단 꼭지점 x좌표, Box의 좌상단 꼭지점 y좌표, Box의 우하단 꼭지점 x좌표, Box의 우하단 꼭지점 y좌표
- (cx,cy,w,h)
: Box 중심 x좌표, Box 중심 y좌표, Box의 너비, Box의 높이
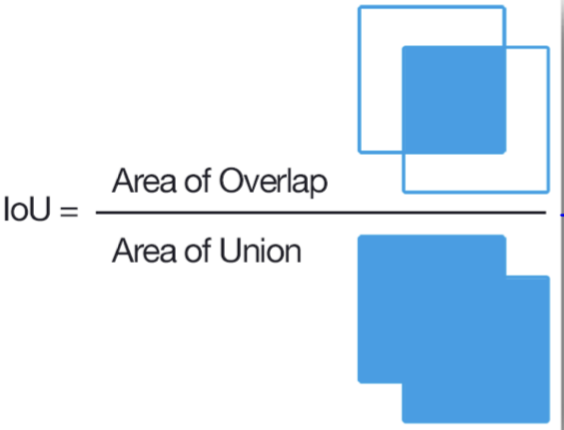
📊 Evaluation metric:IOU(Intersection over Union)
-정답 box와 찾아낸 box 사이의 similarity를 측정하기 위한 metric
-두 box의 교집합 영역 넓이 / 두 box의 합집합 영역 넓이
👍 Input: 이미지 (영상일 경우, 한 Frame)
👎 Output: 객체의 Box좌표 (x,y,w,h), 객체 Box의 Score, 객체 Box의 분류 확률

(출처: Stanford cs231n 강의)
1.3 객체 검출 (Object Detection)
Image Classification와Localization을동시에수행
-주어진 이미지의 객체들이 어떤 것이 분류하고, 그 객체들이 이미지 어디에 존재하는 지까지 알아보기 위한 Task- Input이 이미지가 아닌 영상일 경우 존재하는 물체의 개수가 일정하지 않고 0~N개로 변하기 때문에 난이도가 높은 Task
📊 Evaluation metric:mAP(Mean Average Precision)
-Precision-recall을 기반으로, 각 클래스별 검출 성능(Average Precision)을 측정
-이를 모든 클래스에 대해 평균내어 mAP 계산
👍 Input: 이미지 (영상일 경우, 한 Frame)
👎 Output: 객체의 Box좌표 (x,y,w,h), 객체 Box의 Score(얼마나 신뢰할지), 객체 Box의 분류 확률

(출처:Stanford cs231n 강의)
1.4 세분화 (Segmentation)
: 이미지를 픽셀 단위로 구분해, 각 픽셀이 어떤 클래스에 속하는지 구별하는 문제
- 객체의 위치를 Box로 표시하는 Object Detection보다 더 자세하게 위치를 표현해야 하기에 매우 어려운 문제임
- 주어진 이미지 내 각 픽셀들을 조사하면서 조사 대상인 픽셀이 특정 클래스에 해당하는 객체의 일부인 경우, 해당 위치에 그 클래스를 나타내는
Label index로 표현
-> 어떤 class에도 속하지 않는 경우 배경으로 간주하고 값을 0으로 나타낸다.
📊 Evaluation metric:IoU(Intersection over Union),PA(픽셀 정확도, Pixel Accuracy)
👍 Input: 이미지 (영상일 경우, 한 Frame)
👎 Output: 픽셀별 클래스 분류 결과
4.1) 의미 기반 이미지 세분화 (Semantic Segmentation)
: 분할의 기본 단위 = 클래스
4.2)4.2 인스턴스 기반 이미지 세분화 (Instance Segmentation)
: 분할의 기본 단위 = 객체
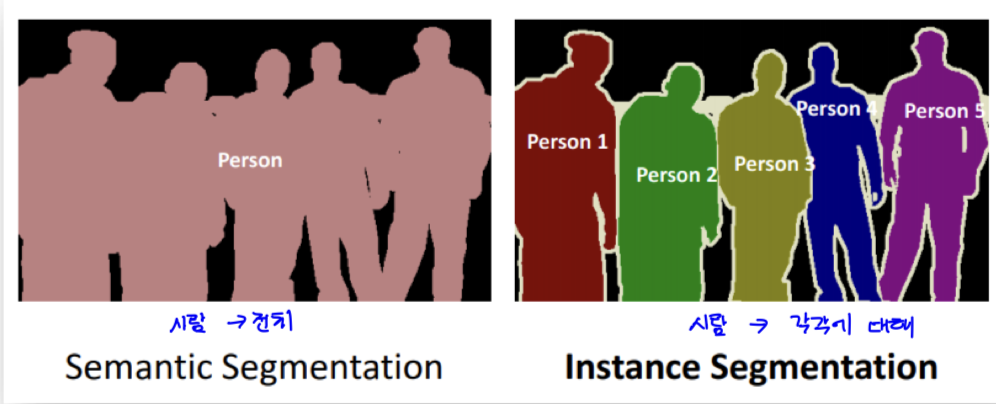
(출처: https://www.analyticsvidhya.com/blog/2019/04/introduction-image-segmentation-techniques-python/)
1.5 특징정 검출 (Keypoint Detection)
- 이미지로부터 사람의 특징점 구조를 검출
- 특징점을 신체 관찰 특징점, 손 특징점, 얼굴 특징점 등으로 나눌 수 있음
- 다양한 Task로 확장 가능함
(Pose Estimation, Action recognition, Face recognition, Tracking, Motion Similarity 등)
📊 Evaluation metric:mAP(Mean Average Precision)
👍 Input: 이미지 (영상일 경우, 한 Frame)
👎 Output: 특징점 위치(좌표)

(출처: https://learnopencv.com/tag/keypoint-detection/)
1.6 이미지 생성 (Image Generation)
진짜이미지와 구별하기 힘든가짜이미지를 생성하는 것이 목표
- GANs (Generative Adversarial Networks) : 데이터 생성을 위한 신경망 구조
생성자(Generator)는 Fake 데이터를 생성하여 구분자를 속이고자 노력하고,구분자(Discriminator)는 생성자에 의해 만들어진 데이터와 진짜 데이터를 구별하기 위해 노력한다.
📊 Evaluation metric: 성능 평가 기법이 애매하다.
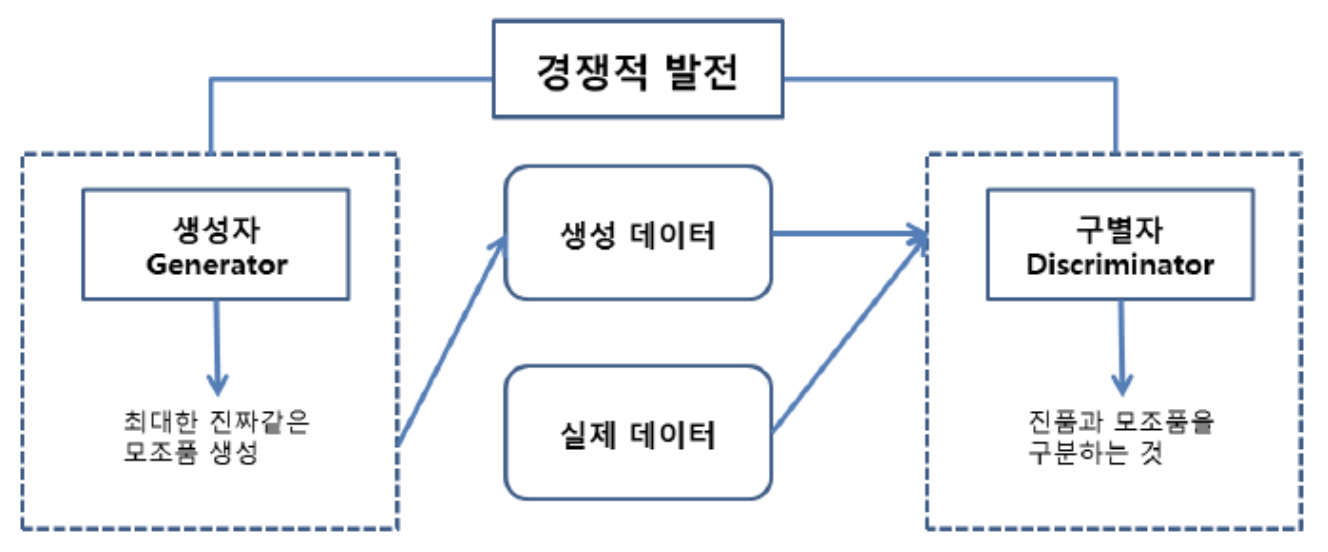
(출처: https://itwiki.kr/w/GAN)
2. Object Detection 논문 추천 리스트

2023년 여름방학을 맞이하여 본격적으로 Object Detection 모델에 대해 공부하고자 합니다! 우연히 Object Detection 논문 추천 리스트인 Paper List from 2014 to 2019(hoya012) 를 보게 되었고, 이는 hoya님의 github를 참고하였습니다. 빨간색 글씨는 "반드시" 읽어야 되는 논문이며 하루에 최소 2개씩 논문을 읽고 저만의 리뷰로 정리하고자 합니다! 파이팅!!
3. End-to-End란?
딥러닝을 공부하다보면 End-to-End라는 말을 정말 많이 들어봤을 것이다. 이 개념을 깊게 공부하고자 jeewoo1025님과 Cara's Moving님의 velog을 참고하여 정리하였습니다!
딥러닝에서 End-to-End란 '한 끝에서 한 끝을 잇는'이라는 사전적 의미를 가지고 있다. 즉,입력에서 출력까지 파이프라인 네트워크 없이 신경망으로 한번에 처리한다는 의미이다. 여기서 파이프라인 네트워크란 전체 네트워크를 이루는 부분적인 네트워크이다. 이는 어떤 문제를 해결해 나가는데 있어서 여러 가지 step이 필요한데, 이 step을 하나의 신경망을 통해서 재배치하는 과정을 의미한다.
또한, End-to-End trainalbe neural network란 모델의 모든 매개변수가 하나의 손실함수에 대해 동시에 훈련되는 경로가 가능한 네트워크를 의미한다. 정리하면, 신경망의 입력 및 출력을 직접 고려하여 네트워크 가중치를 최적화 할 수 있다.
장점은 1) 직접 파이프라인을 설계할 필요가 없다. 즉, 사람이 feature을 추출하지 않아도 된다. 2) 충분할 Labeling 데이터가 있다면 신경망 모델로 해결할 수 있다. 3) 데이터 크기가 클 때 효율적이다
단점은 1) 문제가 복잡할수록 전체를 파이프라인 네트워크로 나눠서 해결하는 것이 더 좋다. 2) 신경망에 너무 많은 계층의 노드가 있거나 메모리가 부족할 경우 이 방식으로 학습할 수 없다.
📚 References
- Image Classification 그림: https://cs231n.github.io/classification/
- Object Detection 그림: Stanford cs231n 강의
- Segmentation 그림: https://www.analyticsvidhya.com/blog/2019/04/introduction-image-segmentation-techniques-python/
- Keypoint Detection 그림: https://learnopencv.com/tag/keypoint-detection/
- GAN 그림: https://itwiki.kr/w/GAN
- https://pongdangstory.tistory.com/424
- https://velog.io/@jeewoo1025/What-is-end-to-end-deep-learning
- https://github.com/hoya012/deep_learning_object_detection
