[프로그래머스 인공지능 미니 데브코스] 수업 정리 -12- [기계학습과 수학]

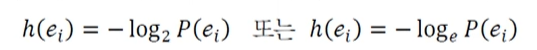
• 기계학습에서 수학의 역할
  수학은 목적함수를 정의하고, 목적함수의 최저점을 찾아주는 최적화 이론 제공
  최적화(optimization) 이론에 학습률(learning rate), 멈춤조건과 같은 제어를 추가하여 알고리즘 구축
  사람은 알고리즘을 설계하고 데이터를 수집

선형대수

기계학습을 이해하기 위한 관련된 기본 선형대수(linear algebra)를 확인

벡터와 행렬

• 벡터(vector)
  : 샘플을 특징 벡터로(feature vector) 표현
  : 요소의 종류와 크기 표현
  요소

  : 데이터 집합의 여러 개 특징 벡터를 첨자로 구분
  여러 개

• 행렬(matrix)
  : 여러 개의 벡터를 담음

: 훈련 집합을 담은 행렬을 설계행렬(design matrix)라 부름

!Tip
벡터는 일반적으로 소문자
행렬은 대문자에 굵게 표현

• 행렬 A의 전치행렬 A^T
  : Iris의 설계 행렬을 전치행렬 표기에 따라 표현하면,

• 행렬을 이용하면 방정식(방정식계 system of equations)을 간결하게 표현가능

• 특수 행렬들
  : 정사각형(정방행렬, square matrix), 대각행렬(diagonal matrix), 단위행렬(identity matrix), 대칭행렬(symmeric matrix)
  

• 행렬 연산
  : 행렬 곱셉(matrix (dot) product) C = AB, 이미지1
  
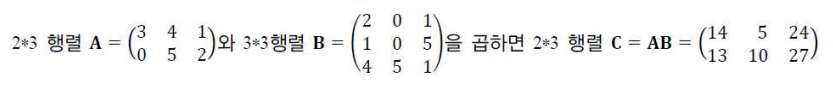
  : 특성
  -교환(commutative)법칙 성립하지 않음 : AB != BA
  -분배(distributive)법칙과 결합(associative)법칙 성립 : A(B+C) = AB+AC이고 A(BC) = (AB)C
  : 벡터의 내적(inner product, 유사도 측정)
  벡터의 내적

  -가지고 있는 기준점에 비추어 봤을 때 입력 데이터가 가지고 있는 데이터(매개변수, 가중치)에 비춰 봤을 때 얼마나 유사한지를 확인 하는 것
  

원하는 값을 구할 때 원하는 위치의 행과 열의 갯수가 매칭이 되어야 곱셈이 된다.

• 행렬 곱셈을 통한 벡터의 변환(transformation)
  : 이때 곱셈을 하면 다른 차원에서 다른 위치로 생겨난다는 것 중요
  
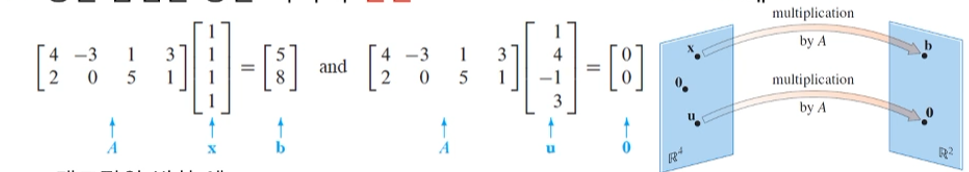
  : 행렬의 곱셈 == 공간의 선형적 변환, 대상이 벡터든 행렬이든 그 대상을 변환시킴

• 텐서(tensor)
  : 3차원 이상의 구조를 가진 숫자배열(array)
  -0차 = 수(scalar)
  -1차 = 벡터
  -2차 = 행렬
  -고차원 ...

  놈과 유사도

• 유사도(similarity) 와 거리(distance)
  : 벡터를 기하학적으로 해석
  
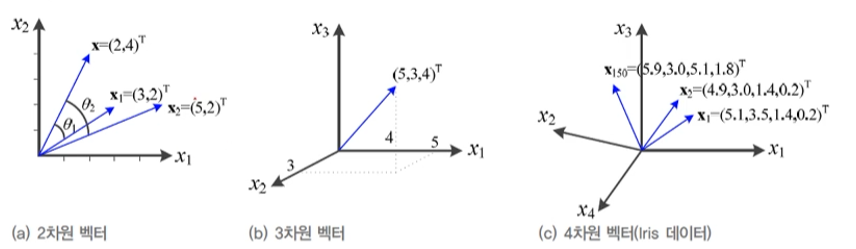
  : 각이 작으면 작을 수록 유사도가 높다.
  : 코사인 유사도(cosine)

• 벡터와 행렬의 거리(크기)를 놈(norm)으로 측정
  : 벡터의 P차 놈

: 1차(p=1) 놈(absolute-value norm), 2차(p=2)놈(euclidean norm), 최대(p=infinite)놈(max norm)

: 행렬의 프로베니우스 놈(Frobenius norm):행렬의 크기를 측정

• 1차 놈과 2차 놈 비교
  : 거리(크기)의 경우, 2차 원, 1차 마름모

퍼셉트론의 해석

• 퍼셉트론(perceptron)
  : 1958년 고안한 분류기(classifier) 모델
  

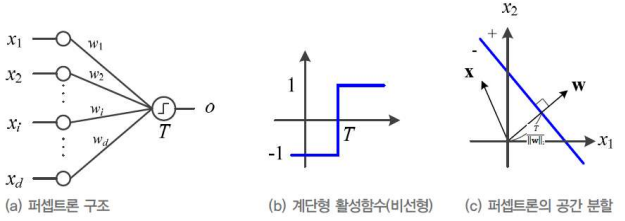
: 활성함수 t로는 계단함수 사용

• 퍼셉트론 물리적 의미
  : 파란직선은 두 개의 부분 공간을 나누는 결정직선(decision line)
  -w에 수직이고 원점으로 부터 T / ||w||2만큼 떨어져 있음
  : 3차원 특징 공간은 결정 평면, 4차원 이상은 결정 초평면

• 학습의 정의
  : 추론(inferring) - 학습을 마친 알고리즘을 현장의 새로운 데이터에 적용하는 작업

: 훈련(training)은 훈련집합의 샘플에 대해 가장 잘 만족하는 W를 찾아내는 작업

• 현대 기계 학습에서 심층학습은 퍼셉트론을 여러 층으로 확장하여 만듦

선형 결합과 벡터 공간

• 벡터
  : 공간상의 한 점으로 화잘표 끝이 벡터의 좌표에 해당
• 선형결합이 만드는 벡터 공간
  : 기저(basis) 벡터 a와 b의 선형결합(linear combination)

: 선형결합으로 만들어지는 공간 벡터공간(vector space)라 부름

• 역행렬(matrix inversion)의 원리

: 변환된 공간을 변환되기 이 전으로 돌려주는 행렬
: 정사각형 A의 역행렬

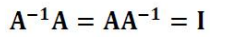
역행렬

• 역행렬을 활용한 방정식 표현과 해

• 행렬의 A의 행렬식(determinant) det(A)

: 역행렬의 존재 유무
-det(A) = 0 : 역행렬 없음
-det(A) !=0 : 역행렬 존재
: 기하학적 의미: 행렬식은 주어진 행려의 곱에 의한 확장 또는 축소 해석
-만약 det(A) = 0, 하나의 차원을 따라 축소되어 부피를 잃게 됨
-만약 det(A) = 1, 부피 유지한 변환/방향 보존 됨
-만약 det(A) = -1, 부피 유지한 변환/방향 보존 안 됨
-만약 det(A) = 5, 5배 부피 확장 되며 방향 보존

• 정부호(definiteness) 행렬

: 성질
-고유값 모두 양수
-역행렬도 정부호 행렬
-det(A) != 0 역행렬 존재

• 정부호 행렬의 종류
  양의 준정부호 0이 아닌 모든 벡터에 대해 >= 0
  음의 정부호 < 0
  음의 준정부호 <= 0

행렬 분해

• 분해(decomposition)란?
  : 정수 3717은 특성이 보이지 않지만, 3x3x7x59로 소인수 분해를 하면 특성이 보임
  -> 행렬도 분해하면 여러모로 유용함

• 고윳값(eigenvalue)과 고유벡터(eigenvector)

고유벡터는 변환하지 않고 그 위치에서 그대로 크기만 커진다.

• 고윳값과 고유 벡터의 효과

• 고유 분해(eigen-decomposition)

: 고유 분해는 고유값과 해당 고유 벡터가 존재하는 정사각행렬에만 적용 가능
: 하지만, 기계 학습에서는 정사각행렬이 아닌 경우의 분해도 필요하므로 고유 분해는 한계

• n*m행렬 A의 특잇값 분해(SVD, singular value decomposision)

• 특잇값 분해의 기하학적 해석
  

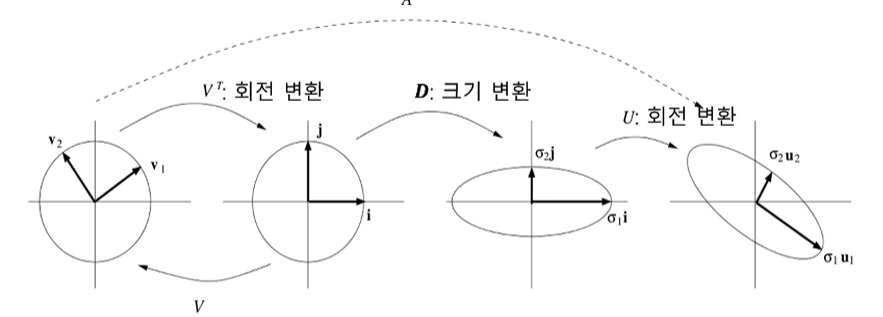
• 특잇값 분해는 정사각행렬이 아닌 행렬의 역행렬을 계산에 사용됨

A의 역행렬은 V은 그대로 쓰고 대각선만 역치를 하면 역행렬이 된다.

확률과 통계

• 기계 학습이 처리할 때 데이터는 불확실한 세상에서 발생하므로, 불확실성(uncertainty)을 다루는 확률과 통계를 잘 활용해야함

확률 기초

• 확률 변수(random variable)
  : 랜덤처럼 보이지만 규칙을 정할 수 있는 것

• 확률 분포(provavility distribution)
  : 확률 질량함수 : 이산 확률 변수
  : 확률 밀도함수 : 연속 확률 변수

• 확률 벡터(random vecotr)

• 곱(and) 규칙 과 합(or) 규칙

• 조건부 확률

joint probability와 구분 필요

• 확률의 연쇄 법칙

• 독립(independence)

• 조건부 독립(condeitional independence)

• 기대값(expectation)

베이즈 정리와 기계학습

• 베이즈 정리(Bayes's rule)

• 베이즈 정리 해석

: 확률 - 정확한 값
: 우도 - 관찰된 값

• 기계학습 적용

: 우도 p(x|y)

사후 확률, 우도와 사전확률을 통해 문제해결

최대 우도(likelihood)

• 매개변수(모수, parameter)를 모르는 상황에서 매개변수를 추정하는 문제.

• 최대 우도
  : 어떤 확률변수의 관찰된 값들을 토대로 그 확률변수의 매개변수를 구하는 방법
  : 일반화 하면,
  
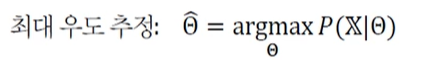
  : 수치 문제를 피하기 위해 로그 표현으로 바꾸면,
  
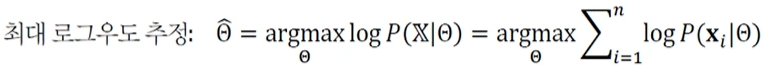
  : 단조 증가하는 로그 함수를 이용하여 계산 단순화

우도 , 확률 분포를 설명하기 위해
'내가 가지고 있는 데이터를 가지고 설명하겠다.' 하여 만드는 대리 그 자체
우도를 통해 우리가 알고 싶은 대상의 확률을 설명할 수 있는 모수의 매개변수를 찾는 방법
기계학습의 하나의 요소이다.
계산을 단순화하기 위해, log, -log(최대를 최소로)를 사용

평균과 분산

• 데이터의 요약 정보로서 평균과 분산(variance)

• 평균 벡터(치우침 정도)와 공분산 행렬(covariance matrix, 확률변수의 상관정도)

유용한 확률분포

• 가우시안 분포(Gaussian distribution)

• 베르누이 분포(Vernoulli distribution)

• 이항 분포(Vinomial distribution)

• 확률 분포와 연관되 유용한 (활성)함수들
  : 로지스틱 시그모이드 함수
  -일반 적으로 베르누이 분포의 매개변수를 조정을 통해 얻어짐
  -함수를 0~1 사이로 바꾸는 함수

: 소프트플러스 함수
-정규 분포의 매개변수의 조정을 통해 얻어짐

• 지수 분포

• 라플라스 분포

• 디랙 분포

• 혼합 분포 (확률 분포를 여러 개를 씀)

• 변수 변환
  : 기존의 확률변수를 새로운 확률 변수로 바꾸는 것
  : 변환 y = g(x)와 가역성을 가진 g에 의해 정의되는 x, y 두 확률 변수를 가정할 때, 두 화률변수는 다음과 같이 상호 정의 될 수 있음

정보이론

• 정보이론과 확률통계는 많은 교차점을 가짐
• 확률통계는 기계학습의 기초적인 근간 제공
  : 해당 확률 분포 추정
  : 확률 분포 간의 유사성 정량화

-> 정보이론 관점에서도 기계학습을 접근 가능
: 불확실성을 정량화 하여 정보이론 방법을 기꼐학습에 활용한 예
-엔트로피, 교차 엔트로피, KL 발산(상대 엔트로피)

• 정보이론 : 사건이 지닌 정보를 정량화 할 수 있나?
  : "아침에 해가 뜬다" 와 "오늘 아침에 일식이 있었다" 라는 두 사건 중 더 많은 정보를 가지는 것은?
  : 정보이론의 원리 -> 확률이 작을수록 많은 정보
  -자주 발생하는 사건보다 잘 일어나지 않은 사건의 정보량이 많음

• 자기 정보
  : 사건(메시지) ei의 정보량
  (단위: 로드의 밑이 2인 경우, 비트 또는 로그의 밑이 자연상수 경우, 나츠)

• 엔트로피(entropy)
  : 확률변수 x의 불확실성을 나타내는 엔트로피
  : 모든 사건 정보량의 기대 값으로 표현
  

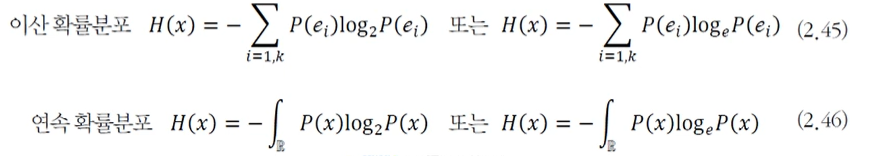
  해당하는 확률 변수가 가질 수 있는, 모든 이벤트에 대한 더한 값
  해당하는 변수가 얼마나 많은 정보를 가질 수 있는가.

• 교차 엔트로피 : 두 확률분포 P와 Q 사이의 교차 엔트로피
  
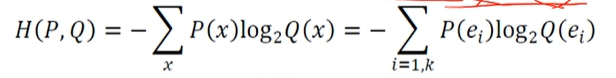
  : 심층 학습의 손실함수로 많이 사용됨
  : 식을 전개하면,
  
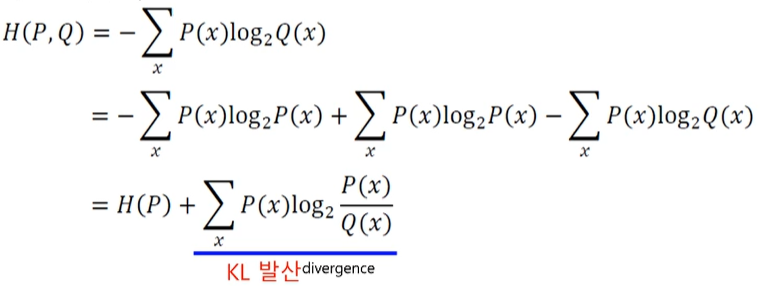
  -여기서 P를 데이터의 분포라 하면, 이는 학습과정에서 변화하지 않음
  -> 교차 엔트로피를 손실함수로 사용하는 경우, KL 발산의 최소화함과 동일

• KL 다이버전스
  : 두 확률분포 사이의 거리를 계산할 때 주로 사용

• 교차 엔트로피와 KL다이버전스의 관계
  
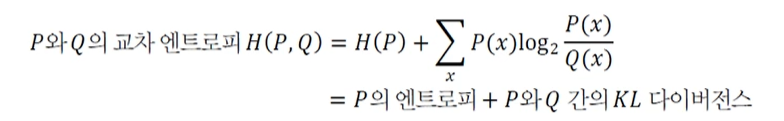
  -> 즉, 가지고 있는 데이터분포 P(X)와 추정한 데이터분포 Q(X)간의 최소화하는데 교차 엔트로피 사용 (p와q가 동일해지면 작아지게 된다)

최적화

• 순수 수학 최적화와 기계학습 최적화의 차이

기계학습의 최적화는 단지 훈련집합이 주어지고, 훈련집합에 따라 정해지는 목적함수의 최저점으로 만드는 모델의 매개변수를 찾아야함
주로 SGD(확률론적 경사하강법)을 사용
-> 손실함수 미분하는 과정 필요 => 오류 역전파 알고리즘

매개변수 공간의 탐색

• 학습 모델의 매개변수 공간
  : 특징 공간의 차원에 비해 훈련집함의 크기가 작아 참인 확률분포를 구하는 일은 불가능함
  : 따라서 기계학습은 적절한 모델(가설)을 선택과 목적함수를 정의하고, 모델의 매개변수 공간을 탐색하여 목적함수가 최저가 되는 최적점을 찾는 전략 사용
  -> 특징 공간에서 해야 하는 일을 모델의 매개변수 공간에서 하는 일로 대치한 셈

• 학습 모델의 매개변수 공간
  : 특징 공간보다 수 배 ~ 수만 배 많은 차원을 가짐
  -> MNIST 인식하는 심층학습 모델은 784차원 특징 고아간, 수십만~수백만 차원의 매개변수공간
  전역 최적해에 가까운 지역 최적해를 찾고 만족하는 경우많음

• 최적화 문제 해결
  : 낱낱탐색(exhaustive search) 알고리즘
  -> 차원이 조금만 높아져도 적용 불가능
  : 무작위 탐색 알고리즘
  -> 아무 전략이 없는 순진한 알고리즘

• 기계학습이 사용하는 전형적인 알고리즘
  : 목적함수가 작아지는 방향을 주로 미분으로 찾아냄
  

미분

• 미분에 의한 최적화
  : 미분의 정의
  
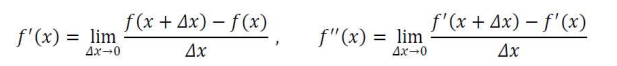
  : 1차 도함수 f'(x)는 함수의 기울기, 즉 값이 커지는 방향을 지시함
  : 따라서, -f'(x) 방향에 목적함수의 최저점이 존재
  

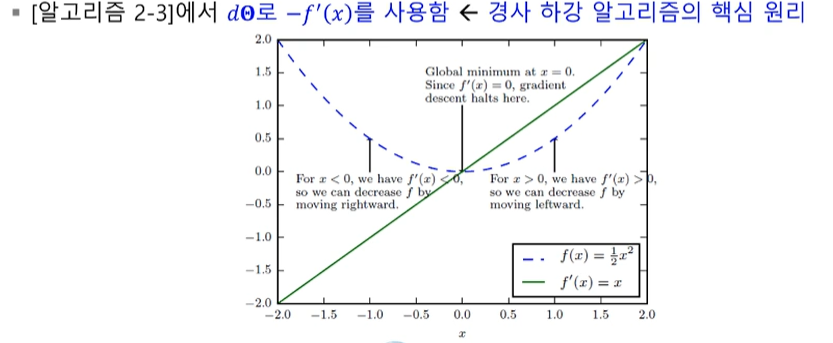
• 편미분
  : 변수가 복수인 함수의 미분
  : 미분 값이 이루는 벡터를 경사도(변화도, gradient)라 부름
  

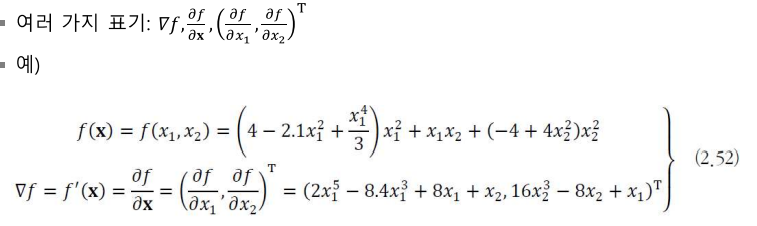
• 기계학습에서 편미분
  : 매개변수 집합은 복수 매개변수이므로 편미분을 사용

• 독립변수와 종속변수의 구분
  : y = wx + b -> 일반적으로 x는 독립변수, y는 종속변수
  : 기계학습에서 예측단계를 위한 해석은 무의미함

• 최적화는 예측단계가 아니라 학습 단계에 필요
  

• 연쇄법칙
  : 합성함수 f(x) = g(h(x))와 f(x) = g(h(i(x)))의 미분
  f'(x) = g'(h(x))h'(x)
  f'(x) = g'(h(i(x)))h'(i(x))i'(x)

  부분부분 구할 수 있다

• 다층 퍼셉트론은 합성함수
  

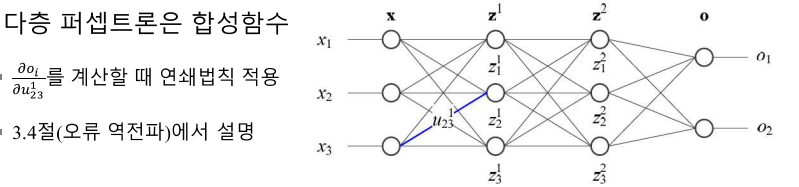
• 야코비언 행렬 : 행렬을 미분
  

• 헤세 행렬 : 야코비언을 2차 미분
  : 2차 편도 함수
  

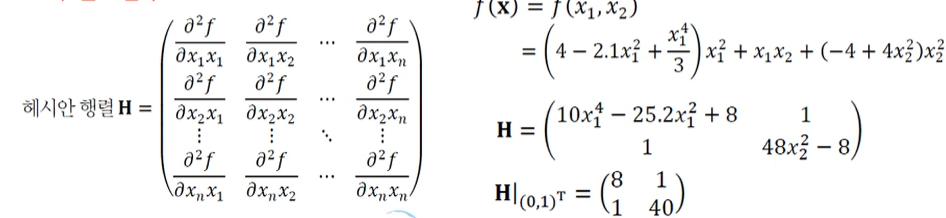
경사 하강 알고리즘

경사 하강법(gradient descent) : 낮은 곳으로 찾아가는 원리
세타 = 세타 - 학습률*기울기
함수의기울기 (경사)를 구하여 기울기가 낮은 쪽으로 반복적으로 이동하여 최소값에 도달
집단(무리, batch) 경사 알고리즘
샘플의 경사도를 구하고 평균한 후 한꺼번에 개애신
훈련집합 전체를 다 봐야 갱신이 일어나므로 학습과정이 오래 걸리는 단점

• 확률론적 경사 하강(SGD, stochastic gradient descent) 알고리즘
  한 샘플 혹은 작은 집단(무리, mini-batch)의 경사도를 계산한 후 즉시 갱신
  작은 무리 단위 : 한 세대(epoch)라 부름(훈련집함 == 세대)

• 경사 하강 알고리즘 비교
  : 집단 경사하강 알고리즘 : 정확한 방향으로 수렴, 느림
  :확률론적 경사하강 알고리즘 : 수렴이 다소 헤맬 수 있음, 빠름

참고 : 기계학습 (오일석)