[Boostcamp AI Tech] Bandit for Recommendation

이성범·2022년 3월 18일

Boostcamp AI tech LinUCB Multi Armed Bandit recsys thompson sampling

Boostcamp AI Tech

목록 보기

46/49

Bandit for Recommendation

00. 학습 내용

Multi-Armed Bandit에 대하여 학습
Thompson Sampling에 대하여 학습
LinUCB에 대하여 학습

01. Multi-Armed Bandit

1) 개요

우리가 카지노에 있다고 가정해보자, 카지노에는 여러 개의 슬롯머신이 존재하고 우리는 여러 개의 슬롯머신 중에서 어떤 머신이 최고의 보상을 줄 수 있는지 정확히 모른다. 그러면 우리가 어떻게 하면 최고의 보상을 줄 수 있는 슬롯머신을 선택할 수 있을까? 이 질문에 대한 해답이 바로 Multi-Armed Bandit 이다.
이 Multi-Armed Bandit은 추천에도 활용될 수 있다. 우리가 추천해주고 싶은 아이템 리스트가 있다고 가정해보자, 우리는 여기서 어떤 아이템을 추천했을 때 유저가 클릭할 지에 대한 정보가 없는 상태이다. 여기서 MAB를 사용하면 우리는 아이템 리스트 중 유저가 클릭할 확률이 제일 높은 아이템을 찾을 수 있고 이를 추천할 수 있게 된다. MAB를 이용하면 각 아이템에 대한 클릭 확률을 구할 수 있게 되기 때문에 어떻게 보면 아이템 리스트에서 아이템의 순서를 매기는 하나의 re-Ranking Method라고도 생각할 수 있다.

Multi-Armed Bandit은 간단하게 말하면 reward을 최대화 하기 위한 매 시간마다의 최선의 action을 Exploration과 Exploitation을 이용해 찾는 방법이라고 할 수 있음
Exploration(탐색)은 더 많은 정보를 얻기 위하여 새로운 arm을 선택하는 것을 말함
Exploitation(활용)은 기존의 경험 혹은 관측 값을 토대로 가장 좋은 arm을 선택하는 것을 말함
ex) 카지노에 5개의 슬롯 머신이 존재하고 우리에게는 총 50번의 기회가 주어졌다고 가정했을 때, 우리는 최고의 슬롯 머신을 찾기 위해서 각 슬롯 머신을 동일한 횟수로 8번씩 또는 그 보다 적은 2번씩 실행해서 최선의 슬롯 머신을 선택해 나머지 기회를 다 투자할 수도 있다. 8번씩 실행하는 경우(Exploration이 많음) 우리는 최고의 슬롯 머신을 선택할 확률은 높아지지만 아 최고의 슬롯 머신을 Exploitation 할 횟수가 적어들어 높은 reward를 얻을 수 없게 된다. 3번 씩 실행하는 경우 (Exploration이 적음) 우리는 최고의 슬롯 머신을 선택할 확률은 낮아지지만 아 최고의 슬롯 머신을 Exploitation 할 횟수가 많아져 최대의 reward를 얻을 수 있는 확률은 높아질 수 있게 된다. 하지만 Exploration이 적다면 잘 못된 슬롯머신을 Exploitation하 확률도 높아지기 때문에 높은 reward를 보장할 수는 없다.
따라서 이처럼 MAB의 Exploration과 Exploitation은 서로 Trade-off관계를 가지기 때문에 적절하고 정밀한 Exploration과 Exploitation을 통해서 최대의 reward를 추정하는 것이 중요

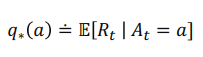
위에서 말한 예시를 간단하게 수학적으로 정의하면 위와 같다.
t는 time step 또는 play number을 의마
$A_{t}$ 는 시간 t에 play한 actruon을 의미
$R_{t}$ 는 시간 t에 받은 reward를 의미
$q_{*}(a)$ 는 action에 따른 reward의 실제 기대값을 의미
우리가 만약에 모든 action에 대한 $q_{*}(a)$ 값을 정확히 할고 있다면 MAB를 사용할 필요가 없음. 하지만 우리는 action에 대한 실제 reward의 true distribution을 모르기 때문에 MAB를 사용해 추정을 하는 것
따라서 MAB는 시간 t에서의 추정치 $Q_{t}(a)$ 를 최대한 정밀하게 구하는 것이 목표라고 할 수 있음
여기서 이제 추정 reward가 최대인 action을 선택하는 것을 greedy action이라고 하며, greedy action 선택이 곧 exploitation을 의미하고, greedy action이 아닌 다른 action을 선택하는 것이 곧 exploration을 의미함
MAB의 가장 기본적인 알고리즘에는 Greedy Algorithm, Epsilon-Greedy Algorithm, Upper Confidence Bound 등이 존재함

2) Greedy Algorithm

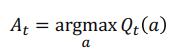
가장 간단한 policy로 지금까지 관측된 개별 머신의 Reward 평균값을 구해서 그 값이 최대인 action을 선택하는 것
문제는 policy가 처음에 선택되는 action과 reward에 크게 영향을 받고, exploration이 부족함

3) Epsilon-Greedy Algorithm

epsilon이라는 확률 값을 바탕으로 greedy action 또는 다른 action을 랜덤하게 선택하는 것
epsilon-greedy는 심플하면서도 강력한 알고리즘으로 베이스라인 모델로 자주 사용됨

4) Upper Confidence Bound

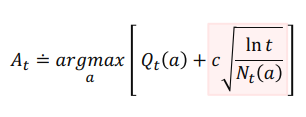
수식의 앞에 부분은 지금 까지 관찰된 action의 reward 평균 값을 의미하고, 뒷 부분은 action a를 선택했던 횟수에 대한 가중치를 의미함
따라서 위 수식에 직관적인 의미는 action의 reward 평균 값을 사용하면서 action이 선택된 횟수에 대하여 가중치를 줌으로써 초기에는 조금더 다양한 action을 선택하는 Exploration을 하고, 후반에 각 action마다 적절한 데이터가 쌓이면 greedy action 만을 선택하여 최적의 보상을 얻는 것을 의미함(log 함수의 초반에 조금더 큰 가중치를 주는 성질을 사용)

5) MAB를 이용한 추천 예시

추천을 MAB에 적용하면, 우리가 추천하는 개별 아이템은 개별 action에 해당하고, 유저에게 아이템을 추천하는 방식이 MAB 알고리즘의 policy에 해당하고, 아이템을 추천했을 때 사용자의 클릭 여부가 reward에 해당함
즉, exploration은 지속적으로 변화하는 유저의 취향 탐색 및 추천 아이템 확장이라고 할 수 있고, exploitation은 유저의 취향에 맞는 아이템 추천이라고 할 수 있음
MAB 알고리즘 자체가 구현이 매우 간단하고 이해하기 쉬우며, 모델이 가볍기 때문에 실제 비즈니스 어플리케이션에 매우 유용함(간단한 Bandit 기법을 적용하여도 온라인 지표가 좋아질 수 있음)

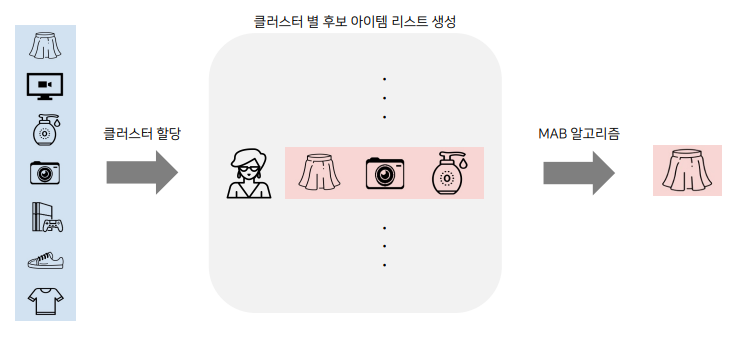
유저 추천의 경우 개별 유저에 대해서 모든 아이템의 Bandit을 구하는 것은 불가능함
확률은 기본적으로 어느 정도 횟수가 반복되면 수렴이 되는데 개인별로 Bandit을 구축한더면 그 데이터의 수가 부족하기 때문에 수렴하지 않아 사용하기 어려움
따라서 비슷한 유저끼리 클러스터링 하여 그룹 내에서 Bandit을 구축하는 것이 효과적임
클러스별로 아이템 후보 리스트를 생성하고, 그 아이템 리스트에 MAB 알고리즘을 적용하여 최적의 아이템을 추천해줄 수 있음
필요한 Bandit의 개수 = 유저 클러스터 개수 x 후보 아이템 개수

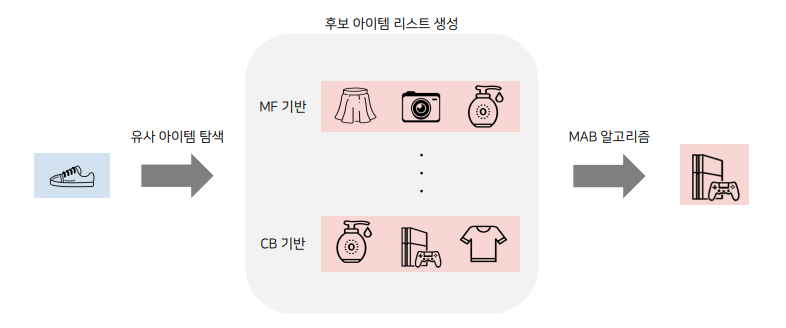
유사 아이템 추천의 경우도 비슷하게 주어진 아이템과 유사한 후보 아이템 리스트를 생성하고 그 안에서 Bandit을 적용하여 사용할 수 있음
필요한 Bandit의 개수 = 아이템 개수 x 후보 아이템 개수

02. Thompson Sampling

Thompson Sampling은 주어진 k개의 action에 해당하는 확률 분포를 구하는 문제임

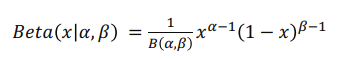
확률 분포는 베타 분포를 사용함. 왜냐하면 베타 분포는 알파, 베타 라는 두 상수에 의해 정해지는 함수인데, 여기서 두 상수 중 하나는 추천을 클릭한 횟수로, 하나는 추천을 클릭하지 않은 횟수로 정의하게 되면 추천을 클릭한 횟수와 추천을 클릭하지 않은 횟수 사이에 확률 분포를 알 수 있게됨
간단하게 설명하면 알파(추천을 클릭한 횟수)라는 값이 베타(추천을 클릭하지 않은 횟수)라는 값보다 커지게 되면 확률 분포에서 샘플링되는 값이 1에 가깝게 된다. 이에 다른 액션들보다 더 높은 값이 샘플링될 확률이 높아져 해당 action을 greedy action으로 선택할 수 있게 되는 것

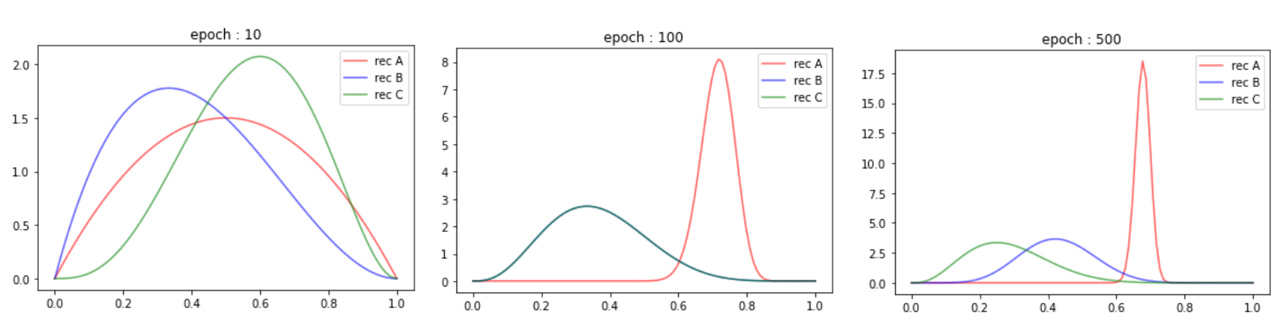
A, B, C 가 각각 선택될 확률을 0.7, 0.5, 0.3 이라고 가정을 하고 Thompson Sampling을 진행해보자.
초기 epoch에는 Exploration이 적기 때문에 추천 C가 가장 높은 샘플링 값이 나올 확률아 더 높다는 것을 알 수 있음(epoch 10)
중반 epoch에는 어느 정도 Exploration이 진행되었기 때문에 추천 A가 가장 높은 샘플링 값이 나올 확률분포를 가짐, 아직 B와 C는 우열을 가리기 어려워 두 값이 모두 적절하게 선택될 수 있음(epoch 100)
후반 epoch에는 이미 충분한 Exploration이 진행되었기 때문에 A, B, C 순으로 가장 높은 샘플링 값이 나올 확률은 가진다는 것을 알 수 있음(epoch 500)
본 실험을 요약하면, Thompson Sampling이 진행됨에 따라 A, B, C의 평균 샘플링 값이 우리가 제일 처음에 지정했던 0.7, 0.5, 0.3 값에 가까워 지는 것
즉, Thompson Sampling을 이용하면 효과적이고 효율적인 Exploration과 Exploitation을 진행해서 최적의 reward를 추정할 수 있게 됨(후반부에는 greedy action만이 선택될 것임)
이미지에 존재하는 간단한 실험 코드