(2206) 벽 부수고 이동하기 (Java)

문제

N×M의 행렬로 표현되는 맵이 있다. 맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로로 이동하려 한다. 최단경로는 맵에서 가장 적은 개수의 칸을 지나는 경로를 말하는데, 이때 시작하는 칸과 끝나는 칸도 포함해서 센다.

만약에 이동하는 도중에 한 개의 벽을 부수고 이동하는 것이 좀 더 경로가 짧아진다면, 벽을 한 개 까지 부수고 이동하여도 된다.

한 칸에서 이동할 수 있는 칸은 상하좌우로 인접한 칸이다.

맵이 주어졌을 때, 최단 경로를 구해 내는 프로그램을 작성하시오.

입력

첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)이 주어진다. 다음 N개의 줄에 M개의 숫자로 맵이 주어진다. (1, 1)과 (N, M)은 항상 0이라고 가정하자.

출력

첫째 줄에 최단 거리를 출력한다. 불가능할 때는 -1을 출력한다.

예제 입력 1

6 4
0100
1110
1000
0000
0111
0000

예제 출력 1

15

예제 입력 2

4 4
0111
1111
1111
1110

예제 출력 2

-1

출처

데이터를 추가한 사람: djm03178, jh05013, Picasso, sait2000, YunGoon
문제의 오타를 찾은 사람: ntopia

알고리즘 분류

그래프 이론
그래프 탐색
너비 우선 탐색

import java.io.*;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    public static int n , m;
    public static int[][] map;
    public static boolean[][][] visit;      // 벽을 부수지 않고 이동한 경우와
                                            // 벽을 부수고 이동한 경우를 각각 따져주기위해 3차원 배열 선언
    public static class Node {
        int x, y, dist, brk;      // 경로와, 벽을 부순 횟수를 체크하기 위해 노드 클래스에 변수 선언
        Node(int x, int y, int dist, int brk) {
            this.x = x;
            this.y = y;
            this.dist = dist;
            this.brk = brk;
        }
    }
    public static Queue<Node> q;
    public static int[] dx = {1, 0, -1, 0};
    public static int[] dy = {0, -1, 0, 1};

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());

        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        map = new int[n][m];
        visit = new boolean[2][n][m];
        q = new LinkedList<Node>();

        // 맵 세팅, 초기 위치 세팅
        for(int i = 0; i < n; i++) {
            String[] strArr = br.readLine().split("");
            for(int j = 0; j < m; j++) {
                int cell = Integer.parseInt(strArr[j]);
                map[i][j] = cell;

                if(i == 0 && j == 0) {
                    q.offer(new Node(i, j, 1, 0));
                    visit[0][i][j] = true;  // 벽을 부수지 않고 이동한 경우를 따져주기 위함
                    visit[1][i][j] = true;  // 벽을 부수고 이동한 경우를 따져주기 위함
                }
            }
        }

        // 목적지 찾기
        bw.write(String.valueOf(findGoal()));
        bw.flush();
        bw.close();
        br.close();
    }
    
    public static int findGoal() {
        while(!q.isEmpty()) {
            Node pc = q.poll();

            // 목적지에 도착했으면 return
            if(pc.x == n-1 && pc.y == m-1) return pc.dist;

            // 인접한 칸 탐색
            for(int k = 0; k < 4; k++) {
                int nx = pc.x + dx[k];
                int ny = pc.y + dy[k];

                // 맵의 범위를 벗어나거나, 이전에 방문한 적이 있는 경우 skip
                if (isNotRange(nx, ny) || visit[pc.brk][nx][ny]) continue;

                // 인접 칸이 벽인 경우
                if(map[nx][ny] == 1) {
                    if(pc.brk == 0 && !visit[1][nx][ny]) {   // 벽을 한번도 부수지 않고 해당 경로까지 온 경우 벽을 부수고 이동한다.
                                        // AND 벽을 부수고 이동한 적이 있는 칸이 아닌 경우에만!
                        q.offer(new Node(nx, ny, pc.dist + 1, pc.brk + 1));
                        visit[pc.brk][nx][ny] = true;
                    }
                }
                // 인접 칸이 벽이 아닌 경우
                else {
                    // 큐에 넣고, 방문처리 (경로 + 1)
                    q.offer(new Node(nx, ny, pc.dist + 1, pc.brk));
                    visit[pc.brk][nx][ny] = true;
                }

            }
        }

        // 이동이 끝나도록 목적지에 도달하지 못했으므로 -1
        return -1;
    }

    public static boolean isNotRange(int x, int y) {
        return (x < 0 || x >= n || y < 0 || y >= m) ? true : false;
    }
}

Feedback

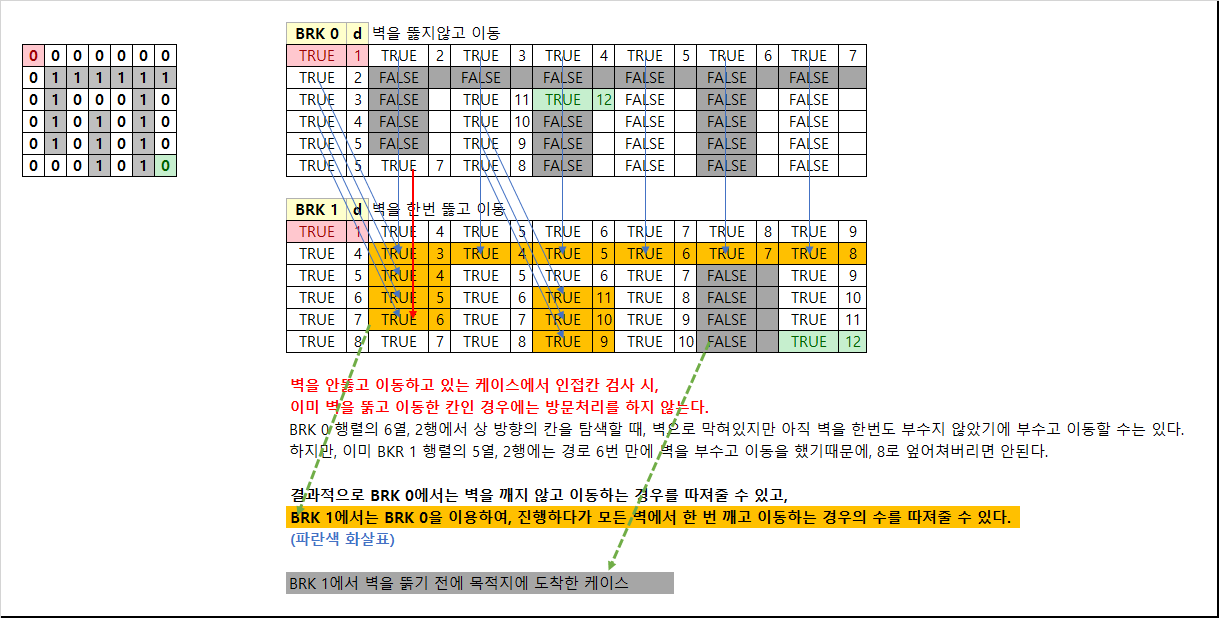
벽을 부수지 않고 이동하는 경우와 벽을 한 번 부수고 이동하는 경우를 한 번에 체크할 수 없다.

어떤 테스트 케이스에서 벽을 부수지 않고 이동하는 것보다, 벽을 부수고 이동하는 경로가 더 짧다고 하자. 그런데 경로 중간에 벽을 부수지 않고 이동하여 방문처리를 한 칸이 있다면, 벽을 부수고 이동하는 케이스에서는 해당 칸에 방문하지 못하게 되는 문제가 있기 때문이다.

따라서 벽을 부순 경우와 부수지 않은 경우에 대한 별도 관리가 필요하여 visit 배열을 3차원으로 선언한다.

음에는 벽을 부수지 않은 채로 이동하다가(visit[0][x][y]) 벽을 만날경우 벽을 부수고 이를 벽을 부순 경우 배열(visit[1][x][y]) 방문처리를 한다. 이런식으로 한다면 해당 테스트 케이스를 진행할 때 만나는 모든 벽을 한 번 부수고 이동하는 경우를 따져볼 수 있다.