7. 딥러닝 모델 학습

딥러닝 학습

Cost를 최적화하는 최적의 w를 Gradient Descent 알고리즘을 통해 계산 (머신러닝과 동일)

Perceptron

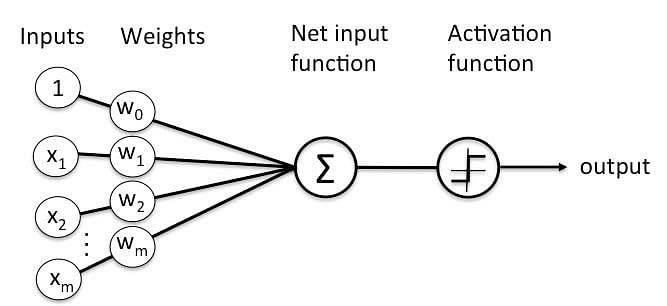
y = w_0x_0 + w_1x_1 + w_2x_2 ...

2. 1번에 활성화 함수를 곱함

activation func * (y = w_0x_0 + w_1x_1 + w_2x_2...)

DNN (Deep Neural Networks)

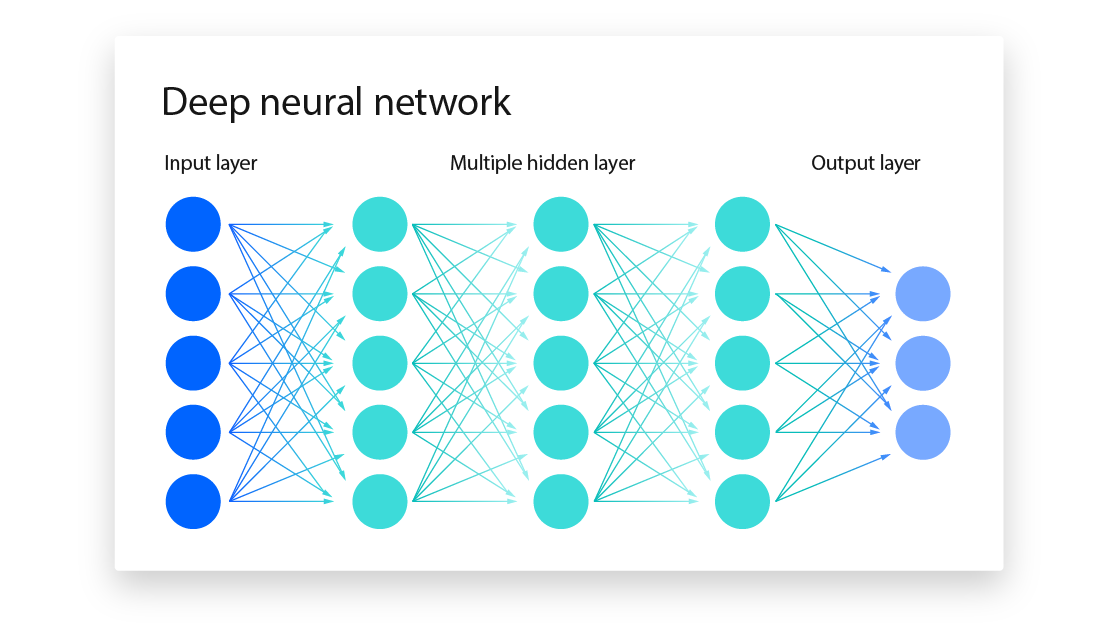
• 입력층(input layer), 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)으로 이루어진 신경망
  - 비선형 활성화 함수를 추가하여 비선형 관계까지 모델링 가능
• 위 그림에서, hidden layer 하나의 노드가 Perceptron(unit)을 의미함

Activation Function

y = wx해서 나온 '결과값'을 각 활성화 함수에 따라 분류함

(ex 시그모이드 함수에서, 0.5보다 작으면 0, 0.5보다 크면 1)

(이진 분류: Sigmoid, 다중 분류: Relu)

Loss function

• 출력값(예측값)과 실제 값 사이의 오차를 계산
• 회귀: MSE (앞 5장), MAE
• 분류: 이진분류 - Binary cross-entropy, 다중분류 - Categorical cross-entropy

Gradient Descent

• 앞 5장과 동일
• 최적의 w를 구함

Back propagation

실제값과 예측값에서 발생된 오차를 구하고, 해당 오차를 output에서 input 방향으로 보냄

• = Gradient Descent 방식을 활용하여 가중치 재업데이트 (Cost 감소시키는 것이 목적)
• 참고로 Foward Propagation(순전파): 딥러닝 모델에 input을 입력하고 output을 얻는 전 과정

Optimizer

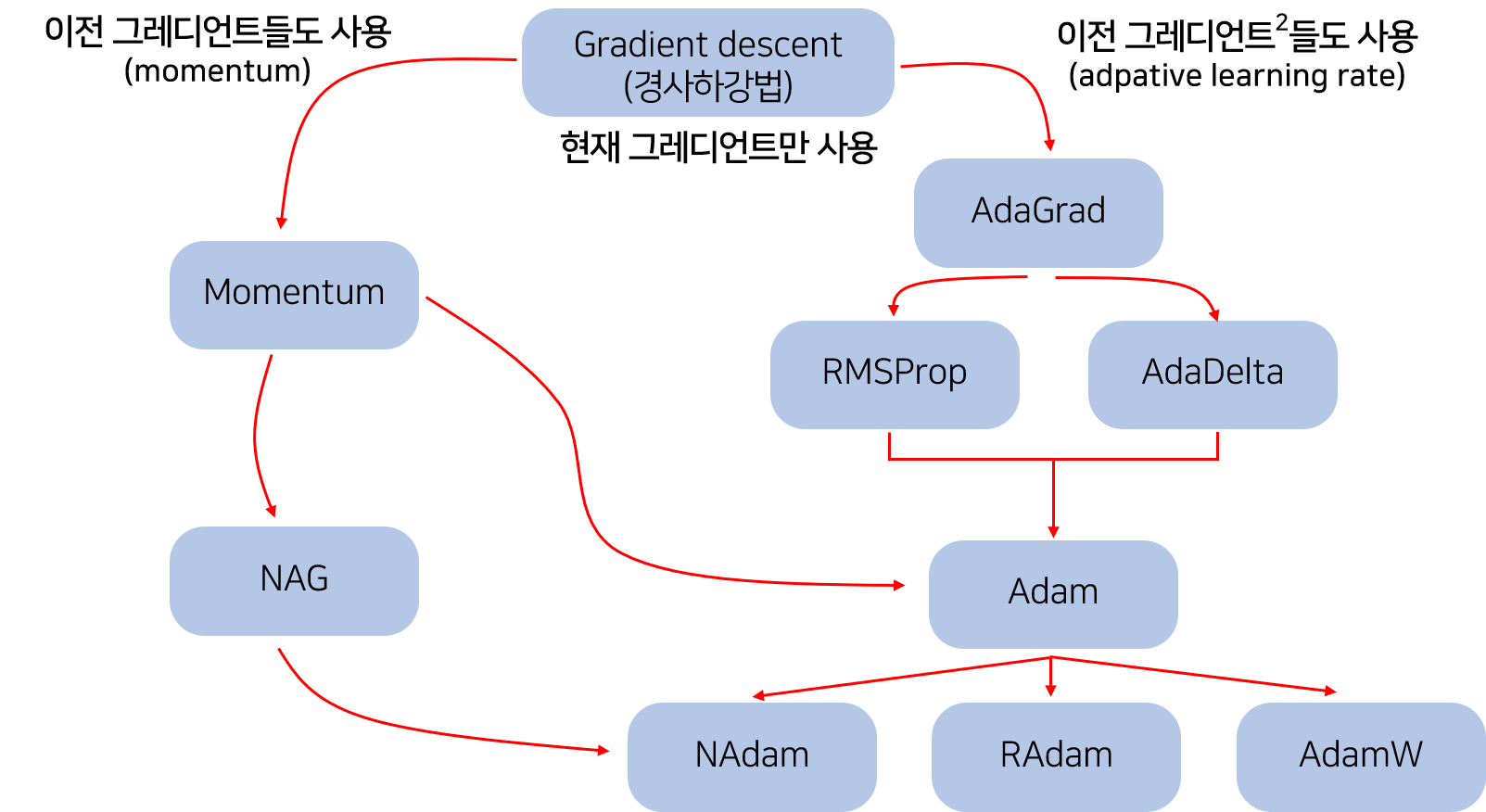
• loss function의 최소값을 찾는 것이 딥러닝 학습의 목표
• 해당 목표 달성을 위해 Optimization을 수행해야 하는데, 이를 수행하는 알고리즘을 Optimizer라 한다.
• 최적의 w를 찾기 위한 알고리즘 (ex Gradient Descent)

Dataset

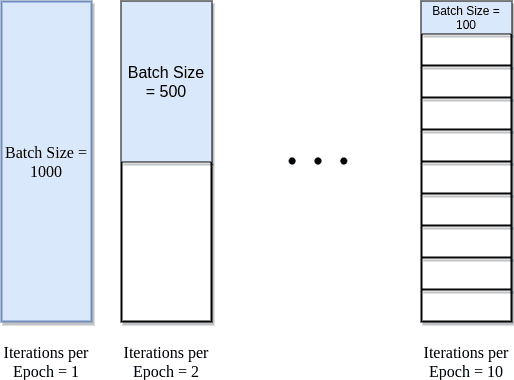
• Epoch: 학습 데이터셋을 전체를 한 번 순회하는 것
• Iteration: 모델이 학습 데이터셋에서 일부 데이터를 사용하여 가중치를 업데이트하는 과정
• Batch size: 각 반복에서 사용되는 데이터의 샘플 수 (Batch: 데이터 샘플)