8. 딥러닝 알고리즘

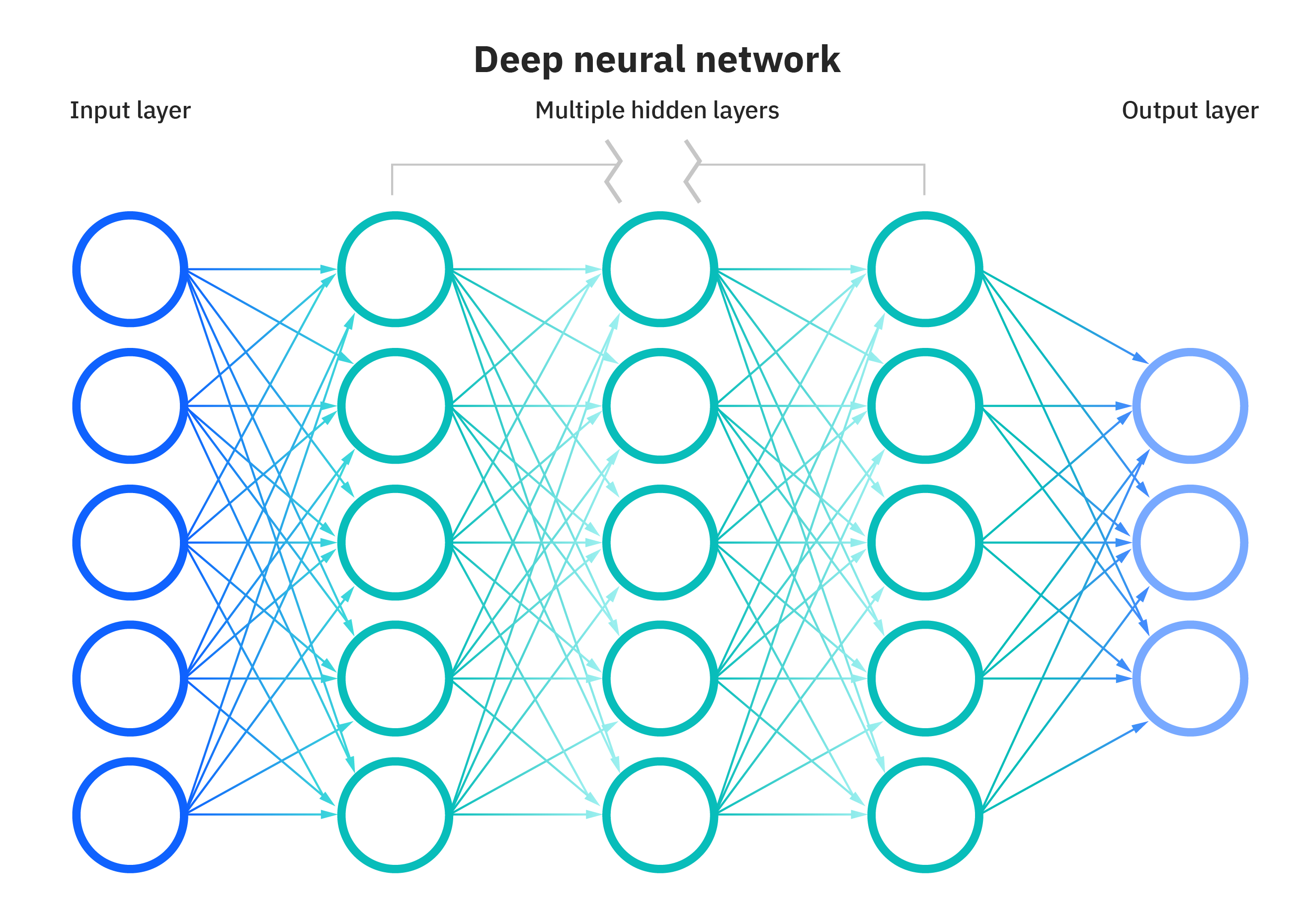
DNN

(7장에 이어)

Dropout

• 신경망의 뉴런을 부분적으로 생략하여 모델의 과적합(overfitting)을 해결해주기 위한 방법중 하나 (0~1사이의 확률로)
  

CNN

- 이미지 처리 시 사용 - 하나의 픽셀 => 하나의 feature - DNN 시 단점: input 이미지를 1차원으로 처리해야 함 (위치정보 소실 가능성), input 사이즈가 커지면 학습이 필요한 가중치가 증가함

특징 추출 영역
: Convolution Layer(각 이미지를 Feature Map이라 지칭함) 및
Pooling Layer(특징 크기 축소시킴) 여러 겹 쌓는 형태

클래스 분류 영역: Fully Connected Layer로 최종 결과값을 출력해내는 것
(여기서부터는 DNN과 동일한 알고리즘)

• Filter를 통하여 최적의 가중치 W를 찾아내는 것이 목표

CNN에서의 필터란?

1. 초기 가중치 설정 시에, 의미없는 값들이 필터에 입력되어 있음
2. 학습을 거치며 필터는 규칙성 있는 형태로 변화
3. 학습된 필터 중 임의적으로 하나를 선택하여 이미지에 합성곱 처리를 하면,
4. 해당 필터 특징에 맞게 어떤 특징이 부각되어 이미지를 출력함

• 원본 이미지에 필터를 씌워 나온 각각의 이미지를 feature map이라 부름

(출처 - https://huangdi.tistory.com/36)

Padding

• (convolution layer의 출력 데이터가 줄어드는 것을 방지): input image의 외곽을 0으로 채움

Pooling

• 이미지 크기를 줄이면서, 주요한 특징은 그대로 유지시키는 것

RNN

- 자연어 처리 시 사용 - 입출력을 Sequential하게 처리함 - 순환구조

h_t = tanh(v*h_(t-1) + u*x_(t) + b_h)

o_t = tanh(w*h_(t-1) + b_o)

• 위 식에서, rnn은 v, u, w등의 가중치를 학습함
• 추가적으로, RNN은 학습 시 2차원 input임

LSTM

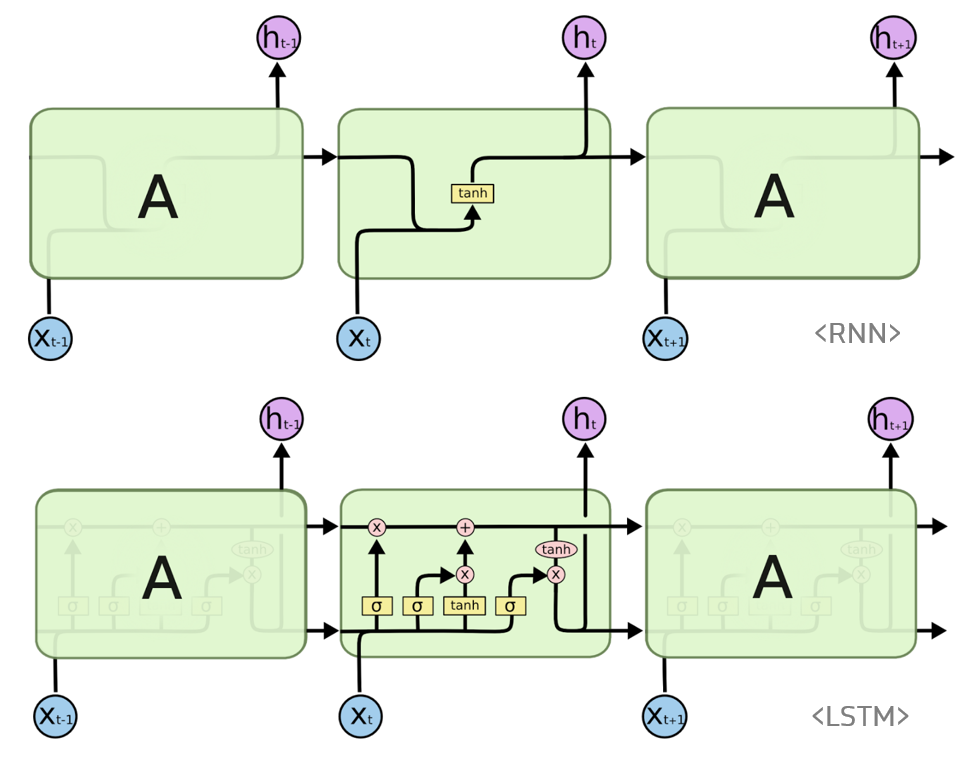
• RNN의 문제점(옆으로 보내는 정보(ex 토큰)(위 그림에서의 h)와 이 정보를 사용하는 지점의 거리가 멀 경우, 역전파 시 Gradient가 줄고 학습능력이 저하됨)
  - 즉, 문장의 길이가 길수록 학습능력이 저하 됨
• 해당 문제점을 보완하기 위해 등장한 것이 LSTM
• cell state(기억해야 할 정보의 상태)가 존재하고, 길이가 긴 input도 처리 가능하도록 설계 됨