Semi-supervised Semantic Segmentation with Error Localization Network, CVPR (2022)
link: https://ieeexplore.ieee.org/document/9878761
source code: https://github.com/kinux98/SSL_ELN

Introduction

Semantic segmentation은 object classification / detection / localization과 더불어 컴퓨터 비전 분야의 대표적인 문제 중 하나이다. 실제로 semantic segmentation 문제를 다루는 많은 양의 논문이 매년 CVPR, ICCV, ICML 등 top-tier conference에 출간된다. 본 논문은 semantic segmentation의 training 과정의 고질적인 문제인 high labeling cost의 해결에 기여한다.

Previous Problem

• 높은 비용의 레이블링: semantic segmentation은 pixelwise classification 문제인 만큼 높은 수준의 train/validation dataset을 요구한다. 하나의 이미지를 레이블링할 때 수 초가 걸리는 class-level의 dataset에 비교했을 때, pixel-level의 dataset의 레이블링은 열 배 이상의 시간이 소요된다. 따라서 semantic segmentation의 dataset은 크기가 비교적 작으며 이미지의 다양성또한 낮다.
• pseudo label의 한계: semantic segmentation에 semi-supervised learning을 적용하는 대부분의 선행연구는 pseudo label을 이용한다. 그러나, pseudo label은 말그대로 실제로 주어진 label이 아닌 labeled data로 학습된 segmentation network가 생성한 label이므로 정확하지 않을 수 있다. inaccurate한 pseudo label로 segmentation network를 학습시키면 에러가 존재하는 방향으로 확증편향(confirmation bias)이 발생해 최종적으로 부정확한 모델이 학습될 수 있다.

Proposed Approach

• binary segmentation network인 ELN(Error Localization Network)을 이용하여 pseudo label의 error가 있을 수 있는 pixel을 무시한 채로 semi-supervised learning을 진행한다. ELN의 error localization capability는 class-agnostic하여 잘 일반화된다.
• ELN을 학습시키기 위해 auxiliary segmentation decoder를 이용한다. main decoder 외에 보조적인 decoder를 이용함으로써 ELN이 발생할 수 있는 다양한 error pixel (pattern)을 경험할 수 있도록 한다. 이때 auxiliary decoder를 main decoder보다 낮은 수준까지만 학습되도록 설정하여 error pixel의 다양성을 높인다.

이로써 저자는 pseudo label을 이용하는 새로운 방법을 제시했으며, semi-supervised semantic segmentation 분야에서 state-of-the-art 수준의 결과를 보였다.

Overall Framework

본 논문에서 제안하는 전반적인 framework의 학습 과정은 다음과 같다.

1. Labeled image를 이용한 main segmentation network의 supervised learning
2. Labeled image를 이용한 auxiliary segmentation network의 supervised learning
3. Labeled image를 이용한 ELN의 supervised learning
4. Unlabeled image와 ELN을 이용한 main segmentation network의 semi-supervised learning
   * 이 과정에서는 mean teacher model이 사용된다.

위 과정 중 (1)~(3)은 (1)의 학습이 충분히 진행된 뒤에는 joint learning을 통해 동시에 진행된다. (4)는 (1)~(3)의 학습이 끝난 뒤에 진행된다.

각 training 과정이 진행될 때 이전 과정은 모두 함께 진행된다. 즉, (4)가 진행될 때 (1)~(3)은 모두 동시에 진행된다.

논문에서 사용된 기본적인 notation은 다음과 같다. 본 포스트에서도 동일한 notation을 사용할 예정이다.

• $D_L$: labeled training data
• $D_U$: unlabeled training data
• $\mathcal E$: segmentation encoder
• $\mathcal D$: segmentation encoder (main)
• $\mathcal D_{aux}^{i}$: $i$번째 auxiliary segmentation encoder

또한, 본 아래와 같은 수학적인 notation 또한 사용되었다.

• $A \oplus B$: 두 개의 tensor $A$와 $B$에 대해 channelwisely concatenate하는 연산을 의미한다. ELN의 input tensor 형성에 이용된다.
• $\lfloor \cdot \rceil$: 반올림 연산을 의미한다. 주어진 실수에 대해 가장 가까운 정수 값을 연산한다.

Supervised Learning

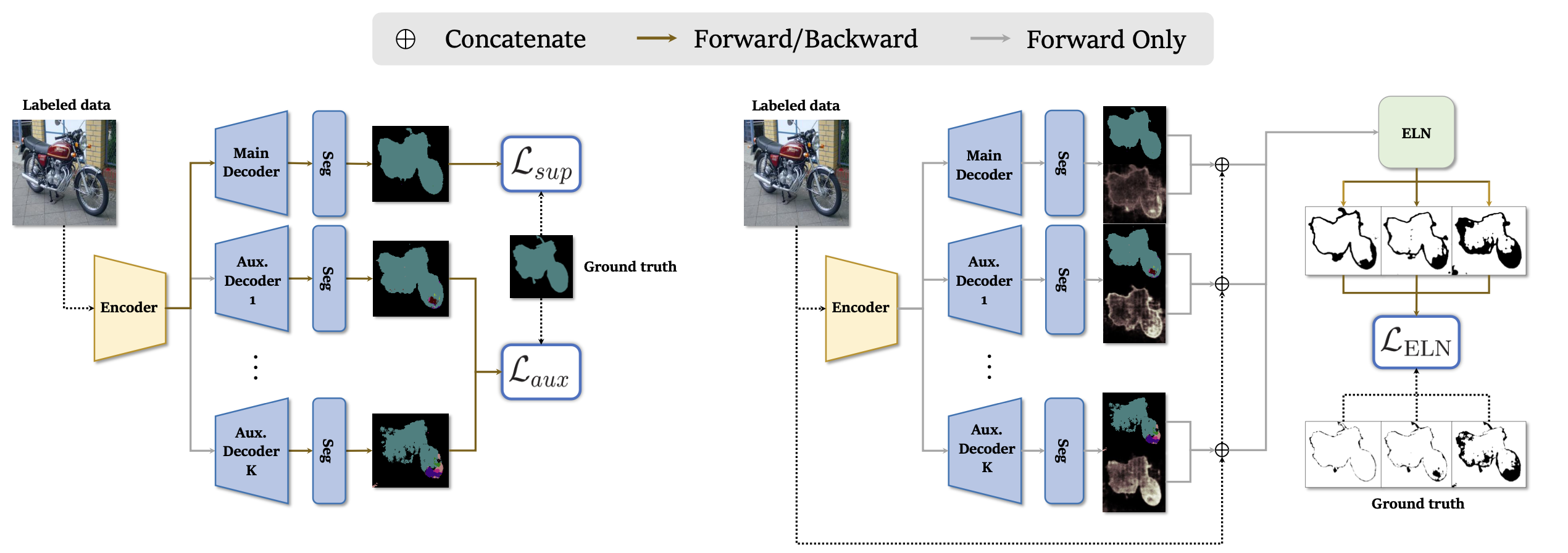
Supervised Learning of Segmentation Network

segmentation network는 pixelwise cross entropy를 이용해 학습된다. segmentation prediction map $P\in \R^{c \times m \times n}$와 ground truth label $Y\in \R^{c \times m \times n}$에 대해 cross entropy loss $\mathcal L_{ce}(P,Y)$는 다음과 같이 정의된다. ($c$는 segmentation network의 class의 개수)

$P_i\in\R^c$와 $Y_i\in\R^c$는 각각 $i$번째 pixel의 classification probability와 ground truth probability를 의미하며, $\log(\cdot)$는 elementwise logarithm이다. $\mathcal L_{ce}(P,Y)$에 대해 supervised learning loss $\mathcal L_{sup}$은 아래와 같이 정의된다.

auxiliary decoder 또한 main decoder와 비슷하게 pixelwise cross entropy를 이용하여 학습된다. 아래 $\mathcal L_{aux}$를 loss function으로 auxiliary decoder는 학습된다. $K$는 framework에서 이용하는 auxiliary decoders의 개수를 의미한다.

$\mathcal L_{sup}$ 식과 마찬가지로 $P^k$는 $k$번째 auxiliary decoder의 segmentation map을 의미한다. 위 식에서 ${\mathbf 1}\left\{ \mathcal L_{ce}(P^k,Y)\gt \alpha^k\cdot \mathcal L_{ce}(P,Y) \right\}$를 제거하면 $\mathcal L_{sup}$과 완전히 동일한 것을 볼 수 있다. 이 부분은 auxiliary decoder의 loss가 main decoder의 loss보다 항상 크도록 만든다. $\mathcal L_{ce}$의 정의에 따라 pixelwise cross entropy는 항상 nonnegative이므로 $\mathcal L_{sup}$과 $\mathcal L_{aux}$를 minimize하는 것은 두 loss를 0으로 만드는 것이다. 따라서 auxiliary decoder의 loss가 main decoder의 loss보다 작거나 같은 경우에는 ${\mathbf 1}\left\{ \mathcal L_{ce}(P^k,Y)\gt \alpha^k\cdot \mathcal L_{ce}(P,Y) \right\}$ 가 $0$이 되어 더이상 학습이 진행되지 못하게 된다. $\alpha^k$는 auxiliary decoder의 학습을 제한하는 hyperparameter이다. $\alpha^k$가 클수록 학습이 더 많이 제한된다. $k$는 exponent가 아닌 index를 나타내는 superscript임에 주의하자.

Supervised Learning of ELN

$B^k=\text{ELN}(X\oplus P^k \oplus E^k)$에 대해 ELN은 아래의 loss를 minimize하는 방향으로 학습된다. 여기에서 $E^k$는 $P^k$의 entropy map으로, prediction map의 불확실성을 정량적으로 나타낸다.ELN의 입력에 ground truth label은 주어지지 않는 것에 집중하자. ELN은 input image, prediction / entropy map만으로 prediction에서 error로 추정되는 pixel을 예측한다.

$M^k\in \R^{m\times n}$는 prediction map의 correctness를 나타내는 binary matrix로, $P^k$와 $Y$가 같은 pixel의 경우에는 $1$, 다른 경우에는 $0$의 entry를 갖는다. $k=0$인 decoder는 main decoder를 의미한다.
다만, segmentation decoders가 pre-training을 거쳤기 때문에 $M^k$는 전반적으로 $1$으로 편향되어 있다. 이를 보완하기 위해 cross entropy의 weight를 재설정한 $\mathcal L_{wce}$를 이용한다.

위 식을 잘 이해하기 위해 summation 안쪽 term을 case로 나눠 작성하면 아래와 같다.

(1) $Y_i=0$인 경우

$\mathbf 0$인 경우가 $\mathbf 1$인 경우에 비해 적으므로 cross entropy term에 1보다 큰 weighting factor를 곱해 loss에 더 크게 기여하도록 변형한다. $\sum_j \mathbf 1\{Y_j=*\}$는 $*$의 값을 가진 entry의 개수를 연산한다.

(2) $Y_i=1$인 경우

$\mathbf 0$인 경우를 scale-up하는 weighting factor를 (1)의 경우에서 곱했으므로 (2)의 경우에는 기존의 cross entropy를 그대로 유지한다.

Joint Learning

위에서 연산한 3개의 loss를 동시에 joint learning하기 위해 아래의 loss를 새로 정의해 minimize한다.

앞서 언급했듯 pre-training stage에서는 $\mathcal L_{sup}$만 minimize한 뒤, pre-training이 끝난 뒤에는 joint learning을 진행한다.

Semi-supervised Learning with ELN

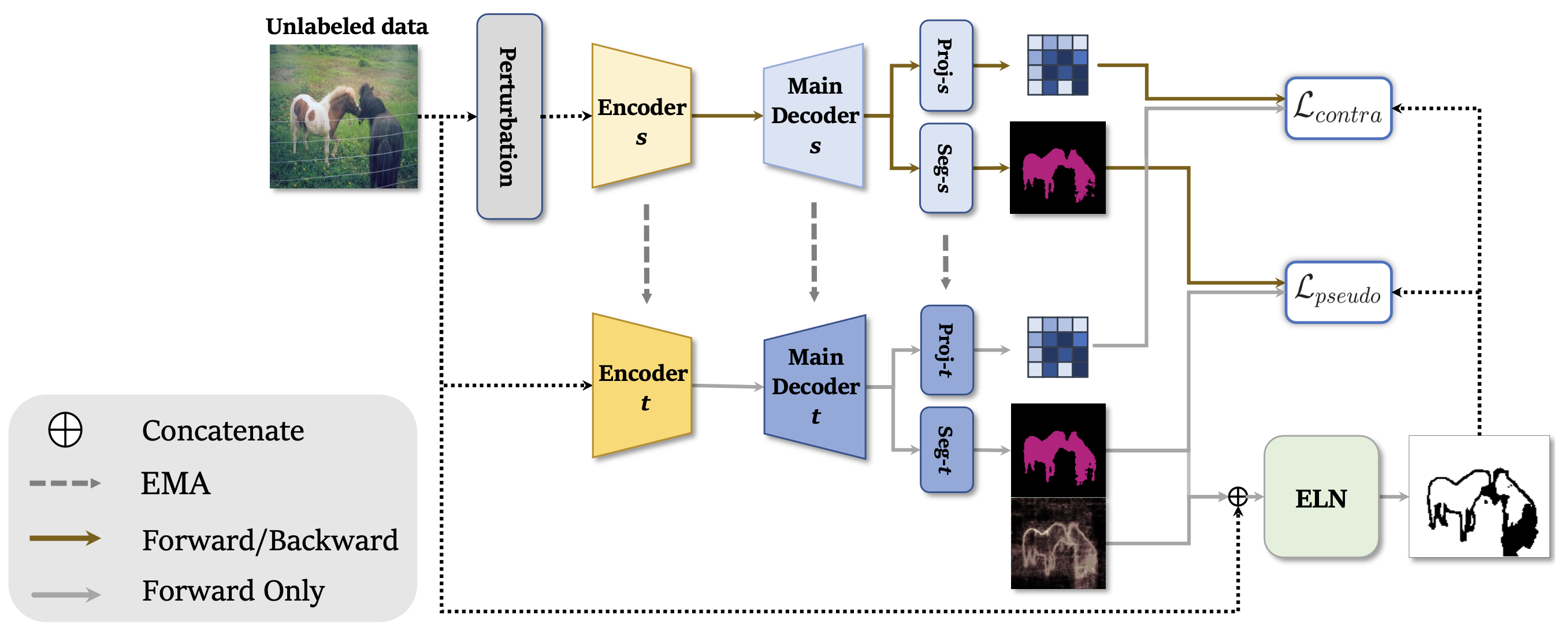
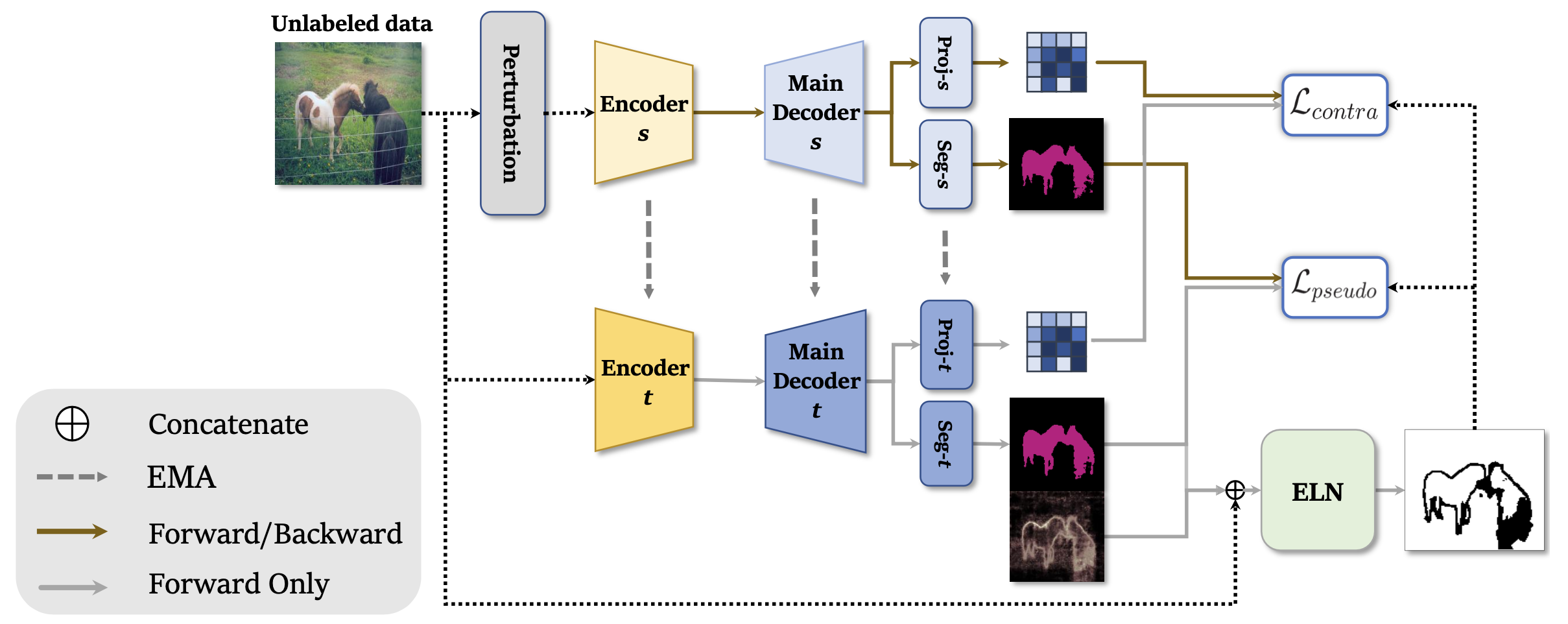
labeled images를 이용한 segmentation network와 ELN의 학습이 끝난 뒤에는 unlabeled images와 ELN을 이용해 segmentation decoder를 학습시킨다. 이때, mean teacher model과 self-training, contrastive learning을 이용한다.

semi-supervised learning 과정에서 unlabeled images의 augmentation을 위해 perturbation이 적용되는데, 본 논문에서는 color jittering과 random grayscale ($p=0.2$)를 적용했다.

Mean Teacher Model

semi-supervised learning on semantic segmentation의 선행연구와 마찬가지로 본 연구에서 또한 mean teacher model을 이용한다. Mean teacher model이란 두 개의 동일한 구조를 가지는 network를 이용하여 학습시키는 것으로, 하나는 teacher model, 다른 하나는 student model이라고 불린다.

loss function의 minimization을 통해 실질적으로 최적화되는 것은 student model이며, 최종적으로 이용되는 model 또한 student model이다. teacher model은 pseudo label을 만드는 network로, student model이 아닌 teacher model이 만들어낸 pseudo label을 이용하여 student model에게 더욱 안정적인 pseudo supervision을 제공할 수 있다.

teacher model의 update는 exponential moving average로 이루어지는데, 이는 아래의 식을 통해 연산된다.

여기에서 $\theta$는 student model의 parameter를, $\tilde \theta$는 teacher model의 parameter를 의미한다. 위 식을 따라 teacher model의 parameter는 student model의 parameter와 조금씩 섞이며 update된다. $\beta\in\left [0,1 \right]$은 hyperparameter로, 보통 $1$에 매우 가깝게 설정된다. teacher model은 student model의 update되는 iteration마다 동일하게 update된다.

Self-training

self-training 과정에서는 teacher model이 만든 pseudo label을 이용해 student model을 cross entropy로 최적화한다. self-training loss는 아래와 같이 정의된다. 논문에서 표현된 식과 다소 다르지만 cross entropy를 이용해 표현하는 것이 가독성을 향상시킬 것이라고 판단해 필자가 식을 수정했다.

이 식에서 $P^a=\mathcal D(\mathcal E (A\cdot X))$는 augmented input image에 대한 student model의 segmentation 결과를, $Y$와 $\tilde B=\text{ELN}(X\oplus \tilde P \oplus \tilde E)$는 각각 teacher model이 만든 pseudo label과 pseudo label에 대한 ELN의 binary error map을 의미한다. $Y$는 $\tilde P=\tilde {\mathcal D}(\tilde{\mathcal E} (X))$에 $\argmax$ 연산을 취해 얻은 one-hot vector이다. $\lfloor \tilde B \rceil$를 pseudo label에 곱함으로써 충분히 신뢰할 수 없는 pixel에 대해서는 학습하지 않는다. 이때, $\lfloor \tilde B \rceil$가 아닌 $\tilde B$를 곱할 수도 있다. 그러나, (1) conservative하게 학습하기 위해, 그리고 (2) $\tilde B$의 값이 절대적으로 pixel의 reliability를 의미하지 않고 특정 값으로 편향되었을 수 있기 때문에 ELN의 output이 0.5를 넘는 pixel에 대해서는 학습하지 않는다.

Contrastive Learning

N-pair loss 언급; 그거 reference는 왜 없는지?

contrastive learning은 동일한 pseudo label을 갖는 pixels은 feature space에서도 동일한 cluster에 존재하고, 그렇지 않는 pixels은 서로 다른 cluster에 존재한다는 가정 하에 진행된다. 이를 loss function으로 작성하기 위해 3가지 set을 정의한다.

• $\Omega_p^i \sube \Z$: $i$번째 pixel과 동일한 pseudo label을 갖는 pixels
• $\Omega_n^i \sube \Z$: $i$번째 pixel과 다른 pseudo label을 갖는 pixels
• $\mathcal V$: $D_U$의 images에서 ELN이 valid하다고 판단한 pixels

위 set에 대해 contrastive loss는 아래와 같이 정의된다. 아래 식 또한 논문의 표현과는 다소 다르다. 이해를 돕기 위해 필자가 약간 수정했음을 밝힌다.

$\mathbf d(f_1, f_2)=\exp (\cos (f_1,f_2)/\tau)$는 metric function으로, 두 feature embedding의 유사도를 연산한다. 이때, $\mathbf d(f_1, f_2)$가 클수록 비슷한 feature를 가진 것으로, 작을수록 서로 다른 feature를 가진 것으로 생각할 수 있다. $\cos(*)$는 cosine similarity를, $\tau$는 temperature hyperparameter이다. 또한, $f_i$와 $\tilde f_i$는 $i$번째 pixel에 대한 각각 student model과 teacher model의 feature embedding을 의미한다.

contrastive learning에서는 anchor와 positive sample의 유사도는 높게, anchor와 negative sample의 유사도는 낮게 학습되어야 한다. (positive sample이란 anchor와 동일한 pseudo label을 갖는 pixel을, negative sample이란 anchor와 다른 pseudo label을 갖는 pixel을 의미한다.) 즉, $\mathbf d(f_i,\tilde f_j)$는 maximize 되어야하며, $\sum_{k\in \Omega_n^i}{\mathbf d(f_i,\tilde f_k)}$는 minimize되어야 한다. 이는 $\mathcal L_{contra}$를 minimize함으로써 최적화될 수 있다.

contrastive learning loss는 Sohn (2016)에서 제안된 multi-class n-pair loss와 유사한 꼴로 정의되므로, 참고하도록 한다.

Joint Learning

두 가지 semi-supervised learning 전략을 동시에 이용해 학습을 진행하기 위해 joint learning loss를 정의한다.

$\mathcal L_{unlabeled}$를 minimize하는 과정에서 $\mathcal L_{labeled}$의 minimization 또한 동시에 발생한다. 최종적인 학습이 종료된 후에 teacher model, auxiliary decoders, ELN은 사용되지 않으며, student model만이 validation / test를 위해 이용된다.

Implementation Details

• segmentation network: DeepLab v3+ with pretrained ResNet backbone

• main encoder: ResNet (-50 / -101)

• main decoder: Seg와 proj로 이루어지며, 각각은 두 개의 $1\times 1$ convolution과 ReLU activation으로 구성된다.

  • Seg: atrous spatial pyramid pooling layer 등으로 구성된 pixelwise classifier

  • proj: feature embedding을 만드는 projection module

• ELN: pretrained ResNet-34 backbone (input이 concatenate된 tensor이므로 ResNet을 적절히 변형하고 fine tune)

Experiments setup

Dataset

	PASCAL VOC 2012	Cityscapes
purpose	segmentation에 일반적으로 이용됨	모델의 generalize 성능 평가
modification	resize to $512 \times 512$	randomly crop to $512 \times 1024$
batch size	$6$	$4$
labeled / unlabeled ratio	$1/20$, $1/8$, $1/4$	$1/8$, $1/4$, $1/2$

$p=0.5$의 random horizontal flip을 적용하여 augmentation한다.

Hyperparameters and Optimizer

• Optimizer: AdamW
  • learning rate: $10^{-4}$
  • weight decay: $10^{-5}$
• Hyperparameter
  • auxiliary decoder의 loss 제한: $\alpha^1=20$, $\alpha^2=50$
  • $\mathcal L_{contra}$의 $\tau$ (temperature): $0.5$
  • exponential moving average $\beta$: $0.995$

Evaluation Metrics

다른 semantic segmentation의 evaluation과 마찬가지로 mIoU를 이용하여 모델의 성능을 평가한다.

Experiment

Segmentation Performance

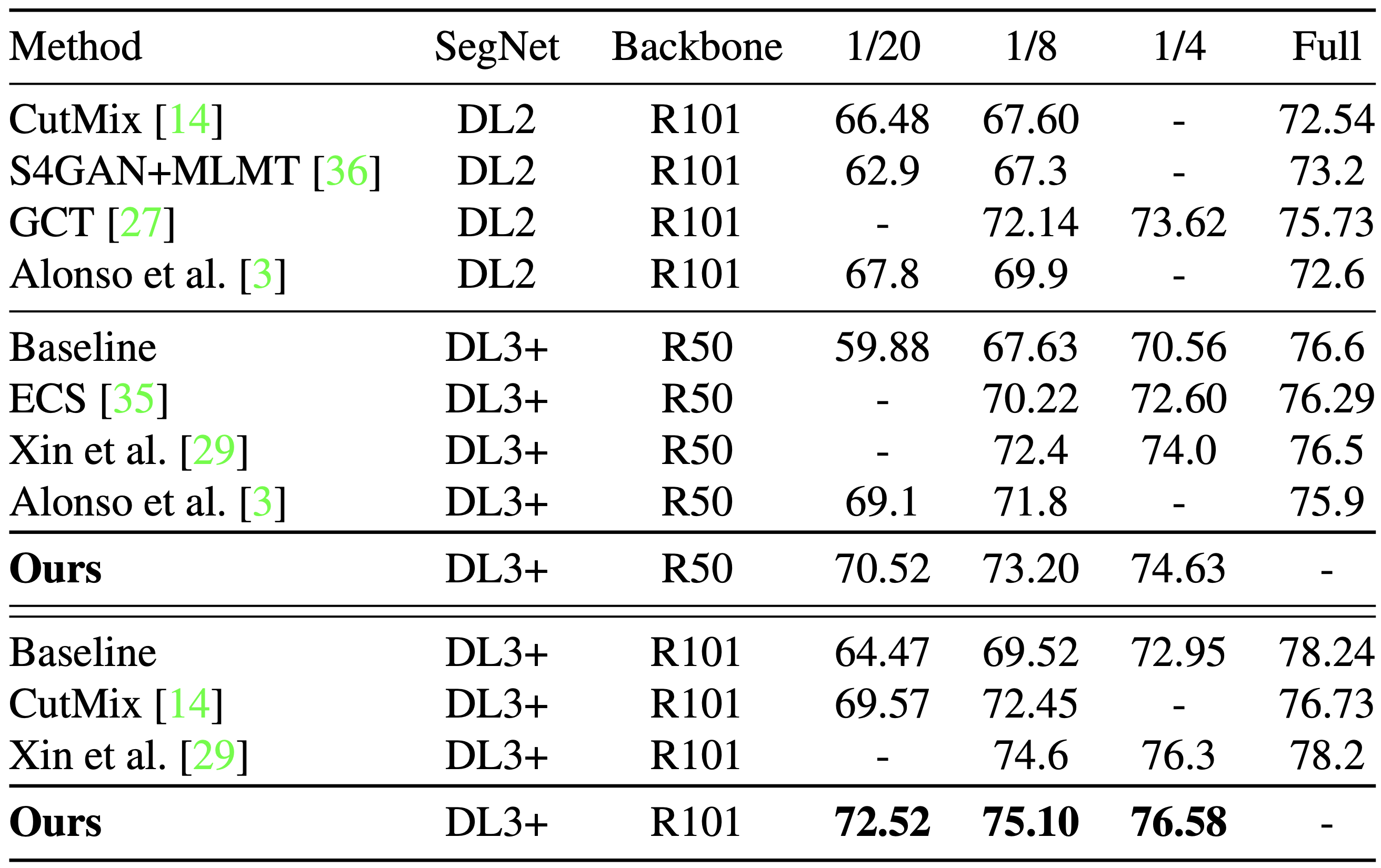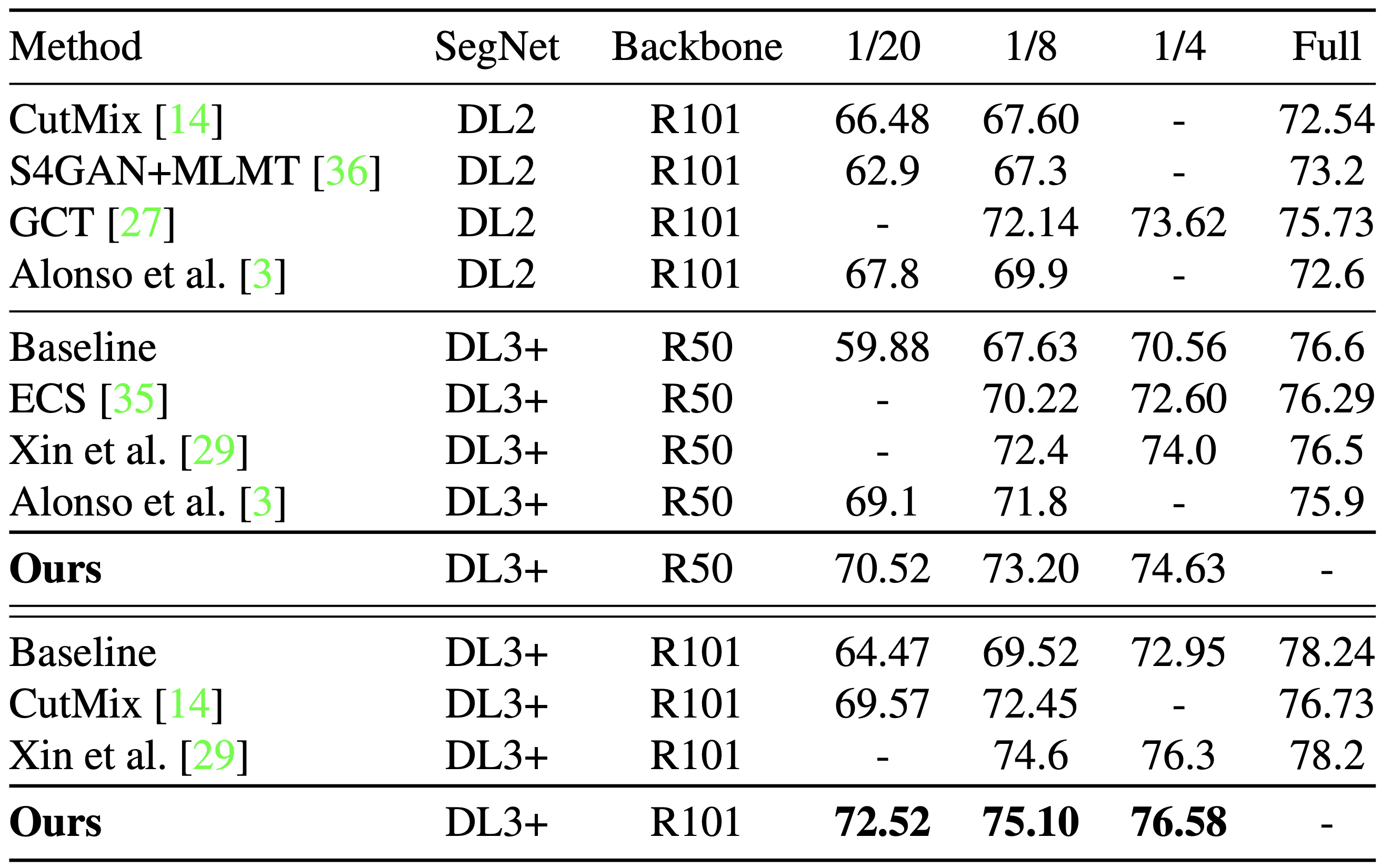PASCAL VOC 2012 val set	Cityscapes val set

두 가지 validation set에 대해 ELN을 사용한 error localization framework이 backbone (ResNet-50, ResNet-101) 에 상관없이 가장 우수한 성능을 보이는 것을 볼 수 있다. 특히, error correction framework을 이용한 ECS($*$ Robert Mendel et al. (2020))에 비해서도 높은 성능을 보였다. Cityscapes에 대한 validation을 통해 ELN framework의 성능은 dataset에 의존하지 않고 잘 generalize한다는 것을 알 수 있다.

$*$ error correction framework은 error localization과 달리 erroneous한 pixel을 무시하여 학습하는 것이 아닌 적절히 error를 수정하여 학습하는 방식을 말한다.

ELN Performance

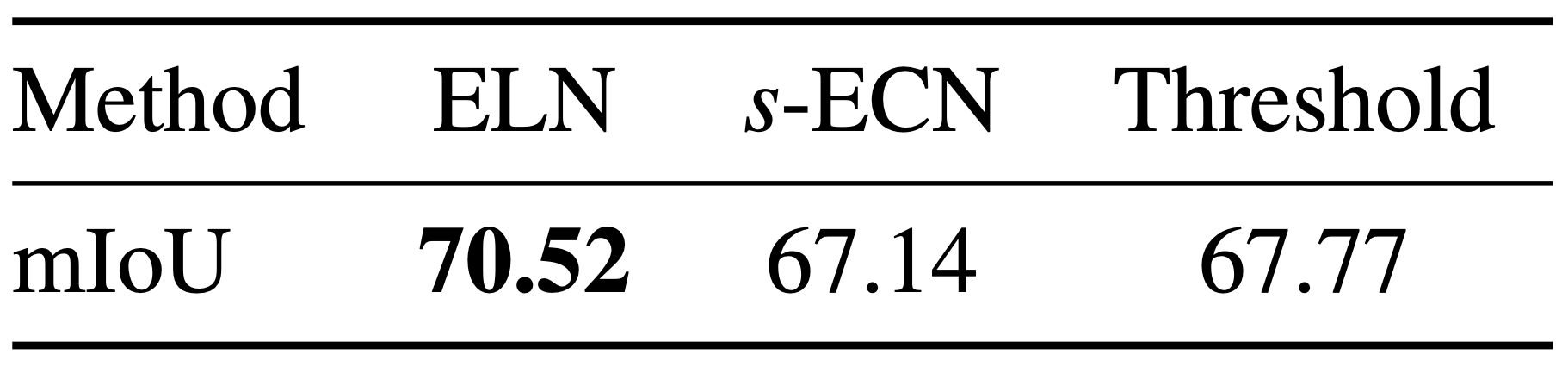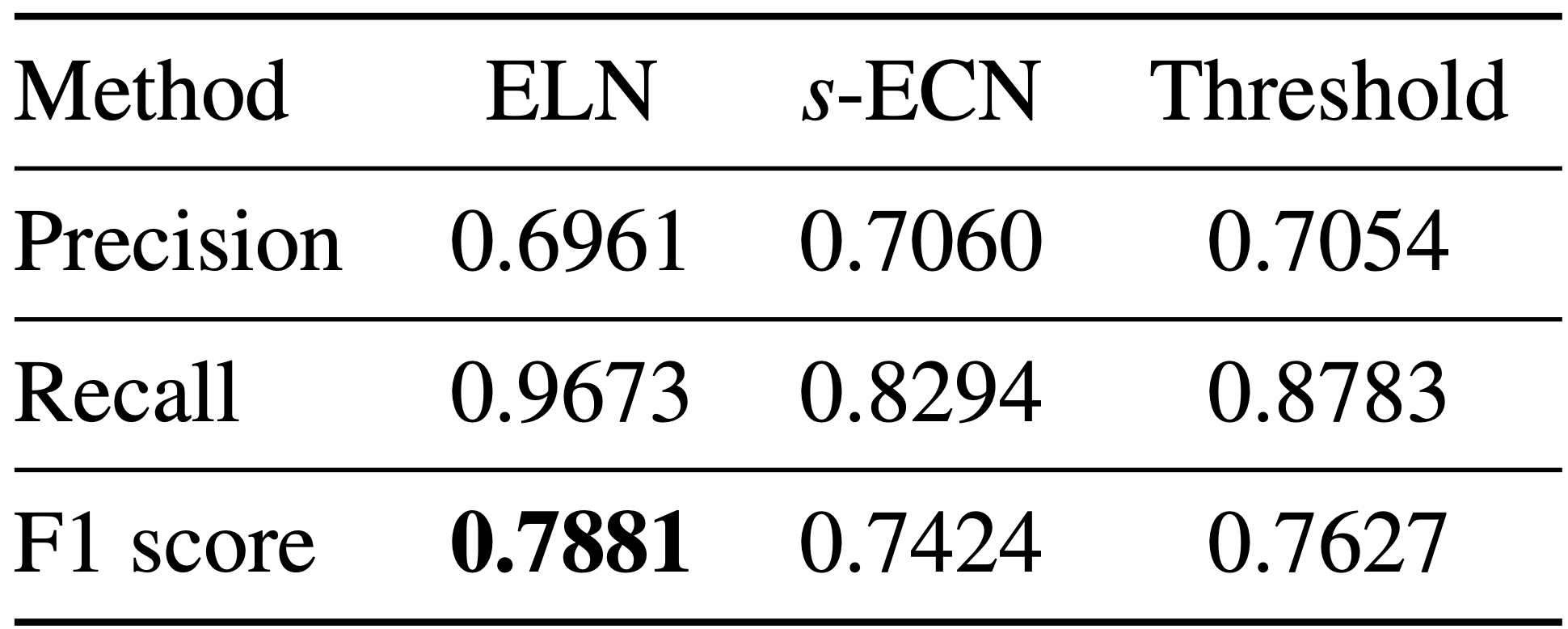위 실험 결과 중 오른쪽 table은 unseen data에 대해 error localization이 어떤 performance를 보여주는지 분석한다. ELN의 performance는 ECN framework과 Threshold($*$)와 비교했을 때 가장 높은 mIoU / F1 score를 얻었다. 특히, ECN framework는 단순한 Threshold 방법보다도 낮은 F1 score를 얻은 것을 확인할 수 있다.

$*$ Threshold는 prediction map에서 특정 임계값 아래의 confidence를 갖는 pixel은 무시한 상태로 학습; 추가적인 network가 사용되지 않는다.

Ablation Studies

저자는 ELN framework의 각 구성요소가 semantic segmentation의 performance에 어떤 영향을 미치는지 보기 위해 ablation study를 진행했다. 실험은 PASCAL VOC 2012 dataset에 대해 ResNet-50 backbone으로 $1/20$의 labeled/unlabeled ratio 상황에서 진행되었다.

auxiliary decoders의 수

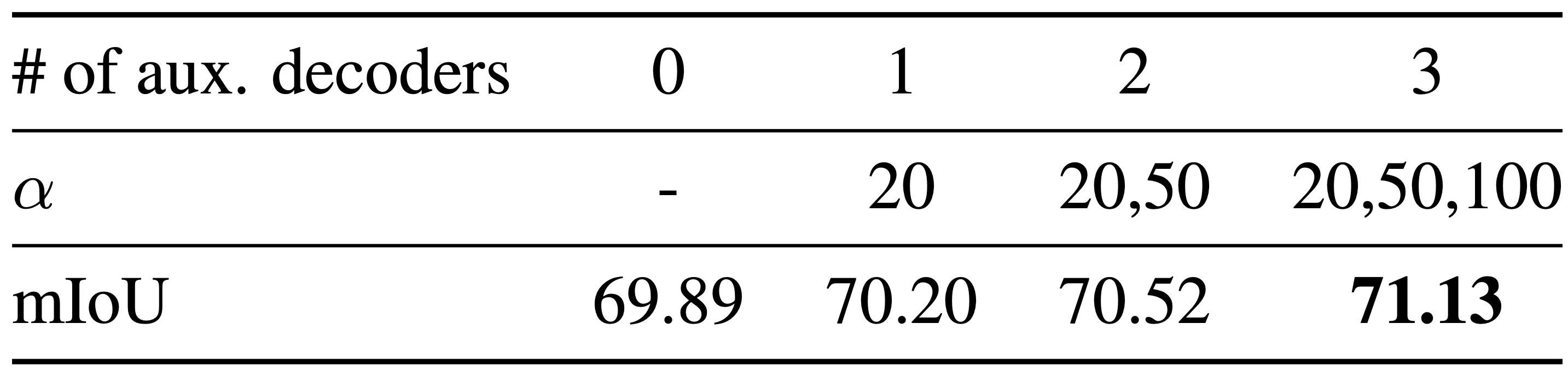
다양한 error pattern을 형성하는데 기여하는 auxiliary decoders의 수와 $\alpha^k$가 증가함에 따라 mIoU가 점점 높아져 성능이 좋게 평가됨을 볼 수 있다. 이때, 2개 ~ 3개의 auxiliary decoders를 추가하는 것만으로도 성능이 증가하는 것을 볼 수 있다.

$*$ $\alpha^k$가 클수록 auxiliary decoder의 학습은 더 많이 제한된다.

loss functions의 조합

$\mathcal L_{unlabeled}$가 jointly learn하는 loss component를 하나씩 제거할 때 mIoU가 어떻게 비교한다. semantic segmentation에 semi-supervised learning을 적용하는 선행연구 대부분은 pseudo label (self-training)을 이용한다. 본 연구에서도 $\mathcal L_{pseudo}$을 이용하여 model을 학습시켰을 때 어느정도의 성능 향상을 보여준다. contrastive learning을 self-training과 함께 이용함으로써 mini-batch 안에서의 다양한 context에 대해 feature embedding을 학습할 수 있게 된다. 이로써 mIoU 또한 가장 높은 점수를 기록한 것을 볼 수 있다.

Conclusion

본 논문에서 제안한 ELN framework를 이용하여 아래와 같은 성과를 얻을 수 있었다.

• ELN은 invalid한 pseudo label을 무시하게 함으로써 semi-supervised learning의 확증편향 (confirmation bias)를 해소한다.
• unseen data에 대해서도 ELN은 효과적으로 작동한다.
• auxiliary decoder를 이용하여 다양한 error pattern을 생성한다.
• ELN을 이용한 semantic segmentation은 state-of-the-art 수준의 performance를 보여준다.

본 연구의 한계

• auxiliary decoder를 이용함에 따라 학습 과정에서 많은 양의 GPU memory와 memory footprint가 요구된다.
• segmentation network가 confident하다고 판단하는 pixel에 대해서는 (i.e., entropy가 낮은 pixel) ELN이 제대로 판단하지 못하는 경향이 있다.