들어가기 전

최근 회사에서 multi sensor를 활용한 이상치 탐지를 해야하는 업무가 있었다.

기존의 있던 rule base의 알고리즘이 사용자가 많아지면서 그 한계를 보인것 같다.

급한데로 rule base의 알고리즘을 조금 수정해서 문제를 어느정도 해결할 수 있을 것으로 보이지만 근본적으로 완벽한 해결책은 아니었다.

때문에 장기적인 관점에서 딥러닝을 활용해서 문제를 해결할 수 있지 않을까하는 생각에 여러 모델을 실험하고 있다.

이번에 만들어본 LSTM 기반 Auto Encoder 모델은 이 task에 처음 시도해본 모델이다.

결론부터 말하자면 우리 task에는 기대만큼 성능이 좋지 못했다.

그 이유가 parameter 문제인지 아니면 preprocessing의 문제인지는 좀 더 조사해봐야 알 수 있겠다.

Paper Review

paper link : LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection

모델 설명

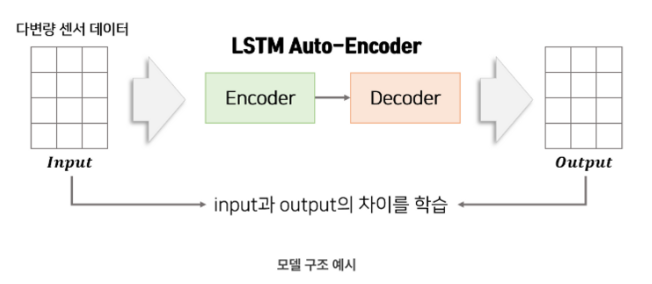
• 정상 데이터를 input으로 입력하여 encoder에서 차원 축소, decoder에서 다시 복원 하는 과정을 거쳐 output이 나온다.
• 인풋과 아웃풋의 차이를 최소화 하도록 학습한다.(MSE 사용)

학습 과정

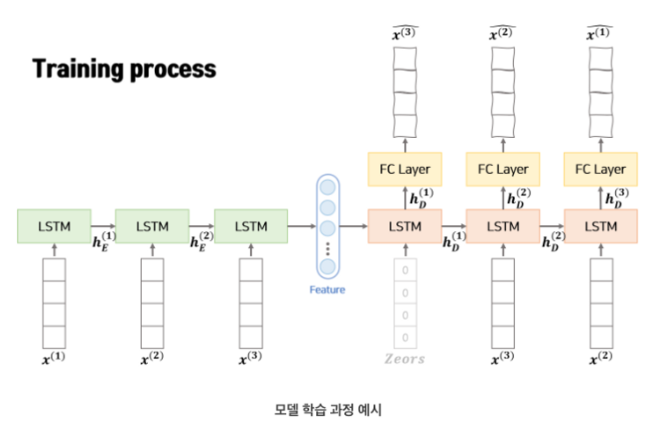
• Teacher Forcing 기법 사용
• initial 값은 0 벡터를 넣음
• $X=\{x^{(1)}, x^{(2)}, ... , x^{(L)}\}$ 형태의 시퀀스가 인풋으로 들어간다. 즉, window size = L로 정해진다.
• 각각의 시점의 x 벡터 역시 $x^{(i)} \in R^m$ 으로 m 차원 벡터로 이루어져 있다.
• encoder에서 학습된 $h^{(L)}_E$ 를(한 번에 들어가는 window size가 L 이므로 마지막에 전달되는 hidden layer의 번호는 L 번이다.) Decoder에 전달해준다.
• 아웃풋은 $X^\prime=\{x^{\prime(L)}, x^{\prime(L-1)}, ... , x^{\prime(1)}\}$ 형태의 역순으로 나온다.

• Decoder에서 $x^\prime$을 예측할때 위와 같은 fc layer를 거친다.

Loss Function

• S, N은 normal 데이터 셋 (데이터 셋에 대한 설명은 밑에서 보다 자세하게 설명)

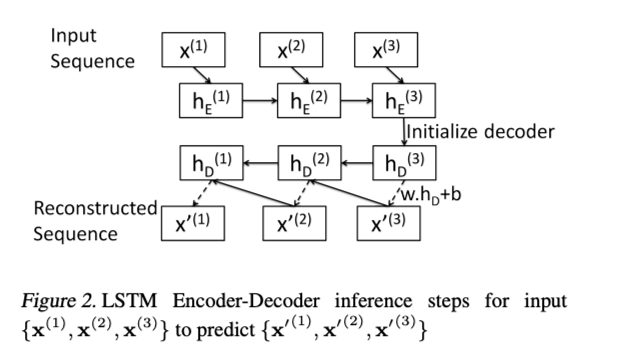
추론 과정

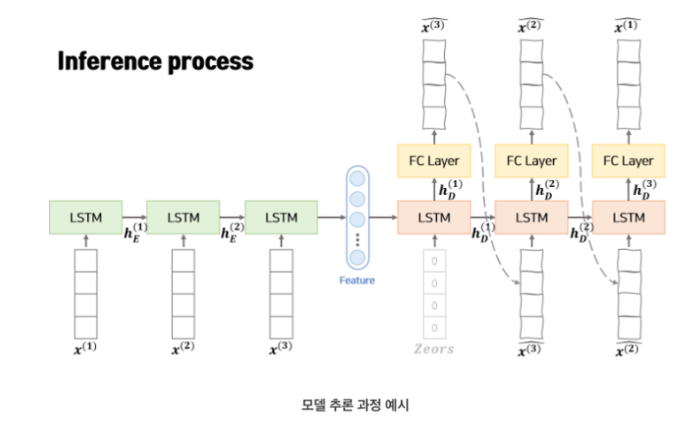
• 추론 과정에서는 teacher forcing 없이 이전 스텝의 데이터를 사용합니다.

Computing likelihood of anomaly

1. Data

   

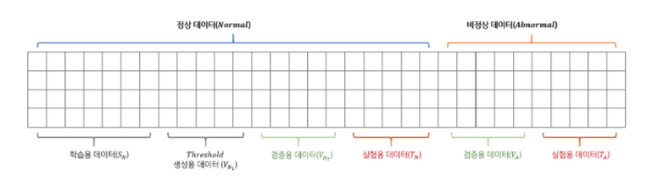
   • $s_N, v_{N1}, v_{N2}, t_N$ 은 정상 데이터, $v_A, t_A$는 비정상 데이터로 분류
   • $s_N$는 학습에 사용
   • $v_{N1}$는 후술할 $\tau$를 구하기 위한 데이터

2. Reconstruction Error

   $e^{(i)} = ||x^{(i)} - x^{\prime(i)}||$

   $e^{(i)}$ : i 지점의 Reconstruction Error

   • $t_i$ 데이터 셋을 활용해 $e$를 구한다.

3. Anomaly Score

   $a^{(i)} = (e^{(i)} - \mu)^T\Sigma^-1(e^{(i)} - \mu)$

4. $\mu$와 $\Sigma$ 구하기

   • 데이터 셋트 $v_{N1}$을 사용하여 $\mu$와 $\Sigma$ 를 구한다.
   • $e$의 평균을 MLE를 통해서 구하고 구한 평균으로 $\Sigma$를 구한다.

5. $\tau (=threshold)$ 구하기

   • $a^{(i)} > \tau$ 이면 지점 $(i)$를 이상치라고 정의함.

6. $F_{\beta}$ Score

   $F_\beta = (1+\beta^2)\times P \times R/(\beta^2P + R)$

   $P : Precision$

   $R : Recall$

   • $F_\beta$ score는 $\beta > 1$이면 $Precision$이, $\beta < 1$이면 $Recall$에 더 가중치를 두는 방식이다.

코드 구현

Dataset

class AD_Dataset(Dataset):
    def __init__(self, timestamp, data, args, normal_mean=None, normal_std=None): 
        # self.idx = idx
        self.timestamp = timestamp
        self.data = data
        self.input_size = args.input_size
        self.normal_mean = normal_mean
        self.normal_std = normal_std
        self.window_size = args.window_size
        
        
        # 정규화
        self.data = (self.data - self.normal_mean) / self.normal_std
        print('정규화 완료')
        
        time_change = np.where(timestamp[:-1]-timestamp[1:]> 60)[0]+1
        self.input_idx = np.array([i for i in range(len(self.data)//self.window_size*self.window_size)]).reshape(-1,self.window_size)
        self.input_idx = np.delete(self.input_idx, time_change//self.window_size, axis=0)
        self.var_data = torch.tensor(self.data, dtype=torch.float)
        
    def __len__(self):
        return len(self.input_idx)
    
    def __getitem__(self, item):
        temp_input_idx = self.input_idx[item]
        input_values = self.var_data[temp_input_idx]
        return input_values

Model

class Encoder(nn.Module):

    def __init__(self, args):
        super(Encoder, self).__init__()
        self.hidden_size = args.hidden_size
        self.num_layers = args.num_layers
        self.droupout = args.dropout
        self.lstm = nn.LSTM(args.input_size, args.hidden_size, arg.snum_layers, batch_first=True,
                            dropout=args.dropout, bidirectional=False)

    def forward(self, x):
        _, (hidden, cell) = self.lstm(x)  # out: tensor of shape (batch_size, seq_length, hidden_size)

        return (hidden, cell)
    
class Decoder(nn.Module):
    
    def __init__(self, args):
        super(Decoder, self).__init__()
        self.hidden_size = args.hidden_size
        self.output_size = args.output_size
        self.num_layers = args.num_layers
        self.droupout = args.dropout
        self.lstm = nn.LSTM(args.input_size, args.hidden_size, args.num_layers, batch_first=True,
                            dropout=args.dropout, bidirectional=False)
        self.fc = nn.Linear(args.hidden_size, args.output_size)
        self.relu = nn.ReLU()
        
    def forward(self, x, hidden):
        outputs, (hidden, cell) = self.lstm(x, hidden)
        pred = self.fc(outputs)
        # pred = self.relu(pred) 
        return pred, (hidden, cell)
    
class LSTMAutoEncoder(nn.Module):
    
    def __init__(self,args)->None:
        
        super(LSTMAutoEncoder, self).__init__()
        
        self.encoder = Encoder(args)
        
        self.reconstruct_decoder = Decoder(args)
        
    def forward(self, input:torch.Tensor) -> torch.Tensor:
        batch_size, sequence_length, var_length = input.size()
        
        encoder_hidden = self.encoder(input)
        inv_idx = torch.arange(sequence_length - 1, -1, -1).long()
        reconstruct_output = []
        temp_input = torch.zeros((batch_size, 1, var_length), dtype=torch.float)
        hidden = encoder_hidden
        
        for _ in range(sequence_length):
            temp_input, hidden = self.reconstruct_decoder(temp_input, hidden)
            reconstruct_output.append(temp_input)
        reconstruct_output = torch.cat(reconstruct_output, dim=1)[:,inv_idx,:]
        
        return reconstruct_output

Train

def trainer(args, model, train_loader, valid_loader):
    optimizer = torch.optim.Adam(model.parameters(), lr=args.lr)  # adam
    loss_fn = torch.nn.MSELoss()  # MSE
    scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.5, patience=5, verbose=True)  # ReduceLROnPlateau : loss 변화량에 기반해 lr 조절
    
    epochs = tqdm(range(1, args.epochs+1))    
    
    ## 학습하기
    best_loss = np.inf
    
    # loss 값 저장
    train_loss_arr = []
    valid_loss_arr = []
    
    for epoch in epochs:
        model.train()
        optimizer.zero_grad()
        train_iterators = enumerate(train_loader)
        
        loss_arr = []
        
        for i, batch_data in train_iterators:
            

            batch_data = batch_data.to(args.device)
            predict_values = model(batch_data)
            loss = loss_fn(predict_values, batch_data)

            loss.backward()
            optimizer.step()
            optimizer.zero_grad()
            
            loss_arr.append(loss.item())
            
    
        
        model.eval()
        eval_loss = 0
        valid_iterators = enumerate(valid_loader)
        
        with torch.no_grad():
            for i, batch_data in valid_iterators:
                
                batch_data = batch_data.to(args.device)
                predict_values = model(batch_data)
                loss = loss_fn(predict_values, batch_data)
                
                eval_loss += loss.mean().item()
                

        eval_loss /= len(valid_loader)

        if eval_loss < best_loss:
            best_loss = eval_loss
            best_model = model
            print('save model')
        else:
            if args.early_stop:
                print("Early Stopping")
                break
        
        scheduler.step(eval_loss)
        
        train_loss_arr.append(np.mean(loss_arr))
        valid_loss_arr.append(eval_loss)
        print(f"epoch : {epoch}, train_loss : {np.mean(loss_arr)}, valid_loss : {eval_loss}")
    
    return best_model, train_loss_arr, valid_loss_arr

Anomaly Score

def get_reconstrcution_error(args, model, test_loader):
    loss = nn.L1Loss(reduce=False)
    test_iterator = enumerate(test_loader)
    reconstrcution_error = []
    
    with torch.no_grad():
        for i, batch_data in tqdm(test_iterator):
            
            batch_data = batch_data.to(args.device)
            predict_values = model(batch_data)
            
            # MAE loss 
            loss_value = loss(predict_values, batch_data)
            reconstrcution_error.append(loss_value.mean(dim=0).cpu().numpy())

    reconstrcution_error = np.concatenate(reconstrcution_error, axis=0)
    return reconstrcution_error

class Anomaly_Calculator:
    def __init__(self, mean:np.array, std:np.array):
        assert mean.shape[0] == std.shape[0] and mean.shape[0] == std.shape[1]  # 평균과 분산의 차원이 같아야함
        self.mean = mean
        self.std = std
    
    def __call__(self, reconstruction_error:np.array):
        x = reconstruction_error - self.mean
        return np.matmul(np.matmul(x, self.std), x.T)

$F_{\beta}$ Score

# precision, recall 구하기
def get_evaluation(label:np.array, anomaly_score:list, threshold:float)->float:
    '''
    anomaly score로 abnormal
    '''
    anomaly_score = np.array(anomaly_score)
    anomaly_score_length = anomaly_score.shape[0]
    
    label = label[:anomaly_score_length]
    
    pred = np.where(anomaly_score>threshold, 1, 0) # abnormal 예측값
    precision = precision_score(label, pred)
    recall = recall_score(label, pred)
    return precision, recall 

# f_score 구하기
def get_fscore(precision:list, recall:list, beta=0.05):
    if (precision==0) & (recall==0):
        return 0
    f_score = (1+beta**2)*precision*(recall/((beta**2)*precision+recall))
    return f_score

참고 자료

1. LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection

2. [코드리뷰]LSTM-based Anomaly Detection - 새내기 코드 여행

3. 분류 성능 평가 지표 : F1 Score, F-Beta Score, Macro-F1 정리

4. 분류성능평가지표 - Precision(정밀도), Recall(재현율) and Accuracy(정확도)