📖 트라이
정의
- 문자열의 집합을 표현하는 트리
특징
- 시간복잡도 측면에선 효율적이지만, 공간복잡도 측면에선 효율적이지 않음
- 트라이의 생성 시간 복잡도는 O(MxL), 탐색 시간 복잡도는 O(L)
(제일 긴 문자열의 길이 : L, 총 문자열들의 수 : M)
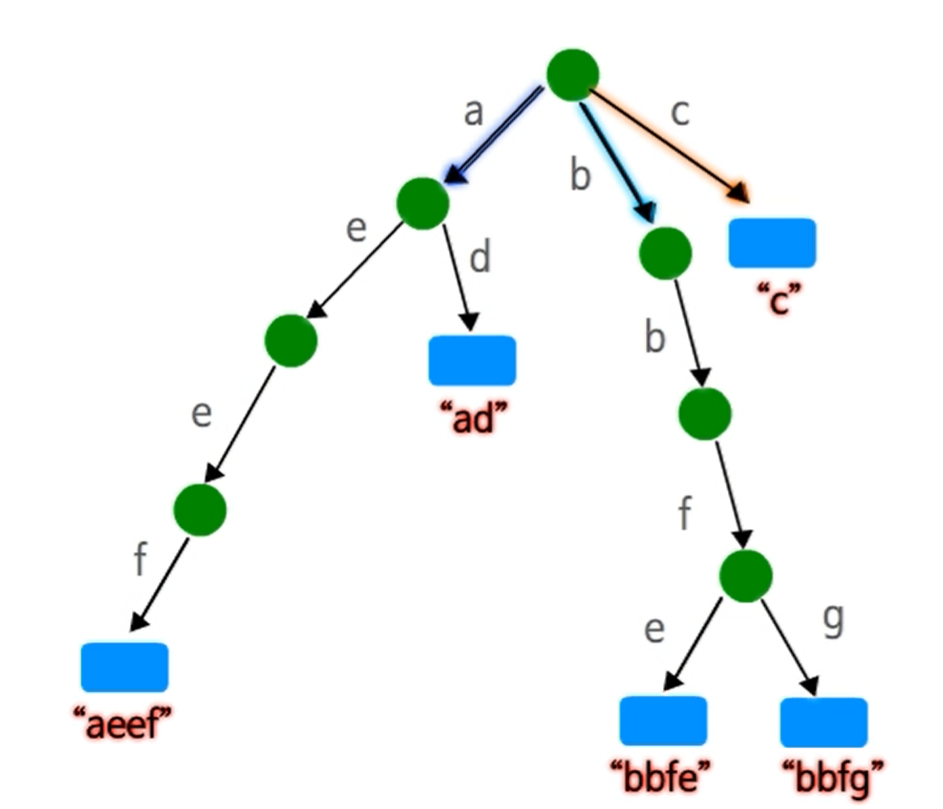
- 트라이의 각 간선은 하나의 문자에 대응
- 같은 노드에서 나오는 간선은 다 다른 문자
- 루트에서 단말 노드까지 이른 경로는 하나의 문자열
💬 접미어 트라이
- 문자열의 모든 접미어를 Trie로 표현
- 하나의 문자열의 모든 접미어를 포함하는 트라이의 압축된 표현
- 공간 복잡도를 줄이기 위해 접미어 배열이 알려짐
- 문자열 연산에 필요한 알고리즘을 빠르게 구현 가능
- 루트를 제외한 내부 노드들은 최소 2개의 자식 가짐
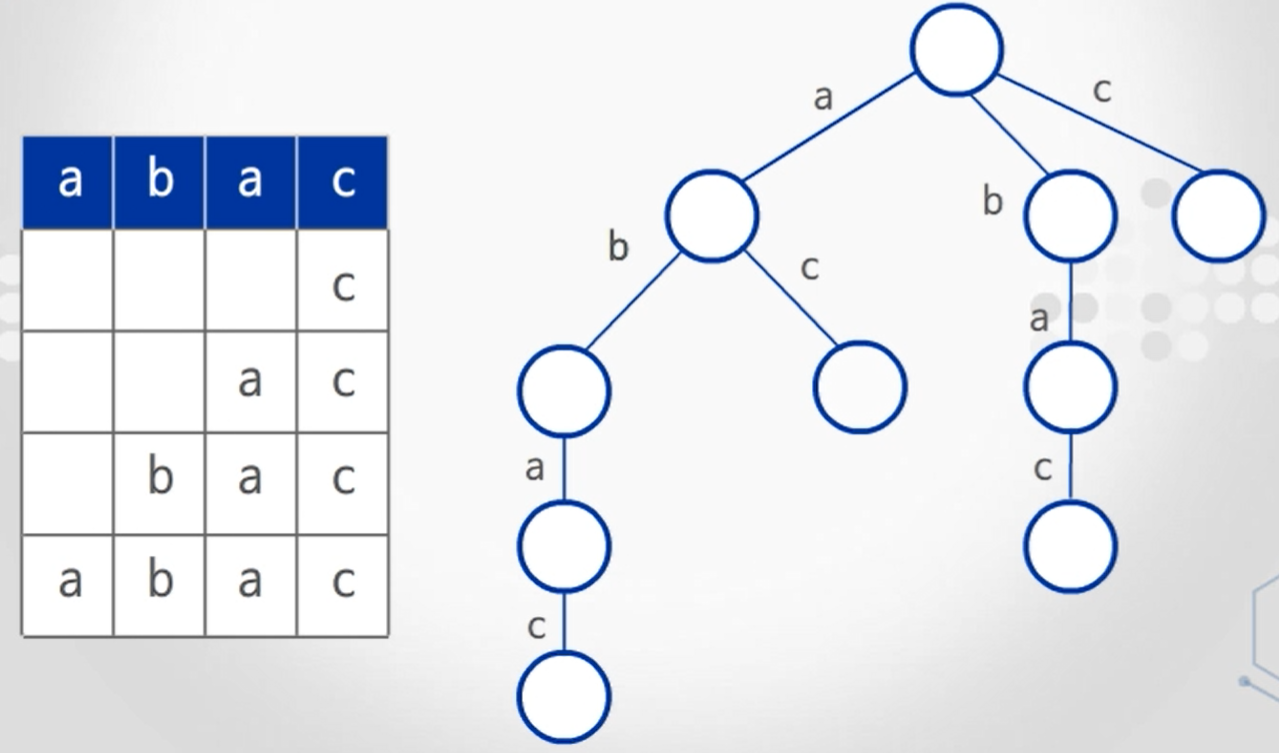
접미어 트라이를 이용한 연산
- 부분 문자열 검사
ex) ba가 abac의 부분 문자열인가 - 두 접미어의 최장 공통 접두어 찾기
ex) abac와 ac의 최장 공통 접두어는 무엇인가 - 사전적 순서로 정렬된 k번째 접미어 찾기
ex) abac에서 사전적 순서로 3번째 접미어는 무엇인가 - 문자열 매칭
1. 접미어 Trie를 통한 부분 문자열 검사
- 한 문자식 루트에서 대응되는 간선 따라가기
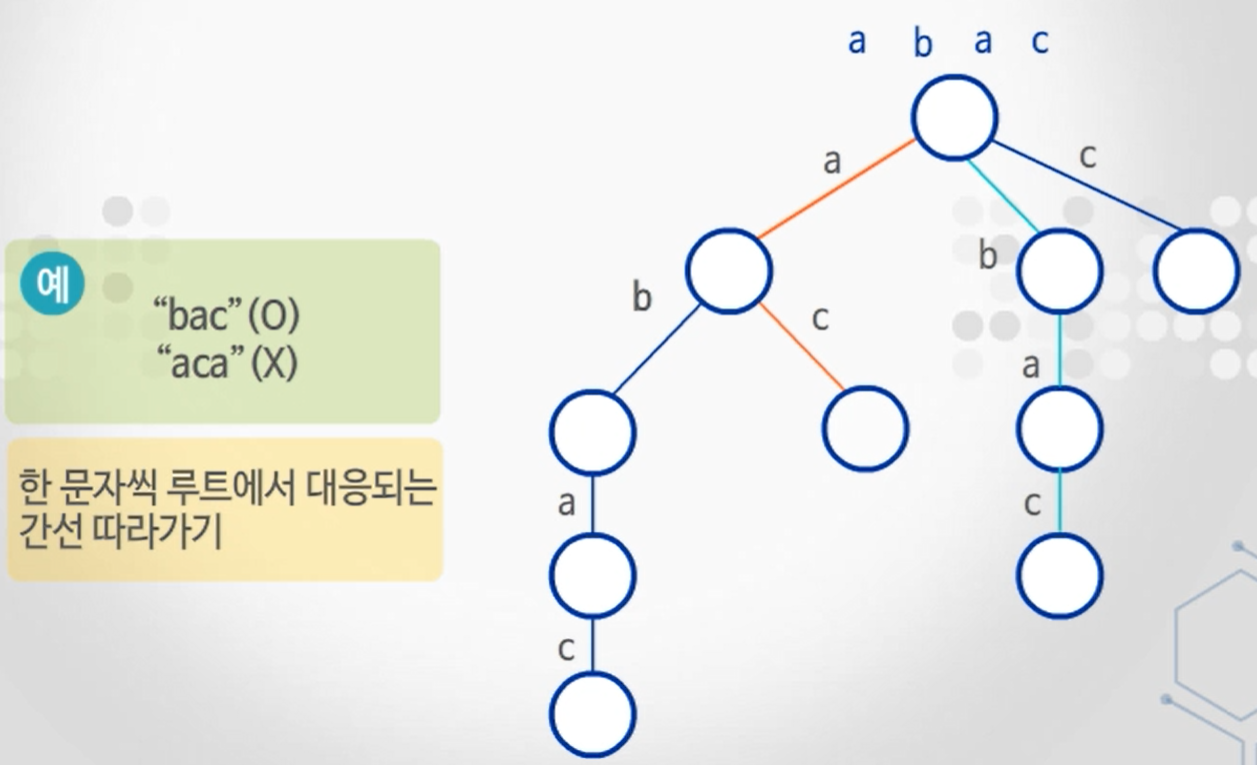
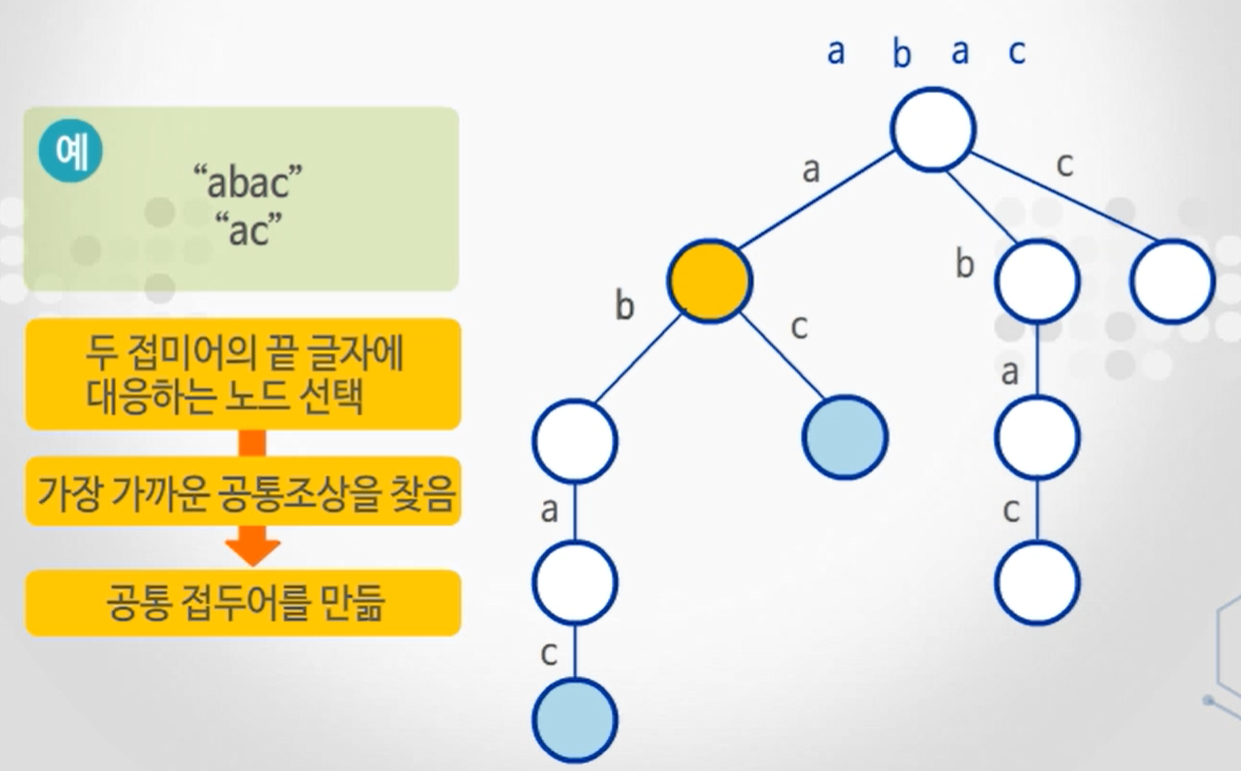
2. 두 접미어의 최장 공통 접두어
- 두 접미어의 끝 글자에 대응하는 노드 선택
- 가장 가까운 공통조상 찾기
- 루트에서 공통조상까지가 최장 공통 접두어가 됨
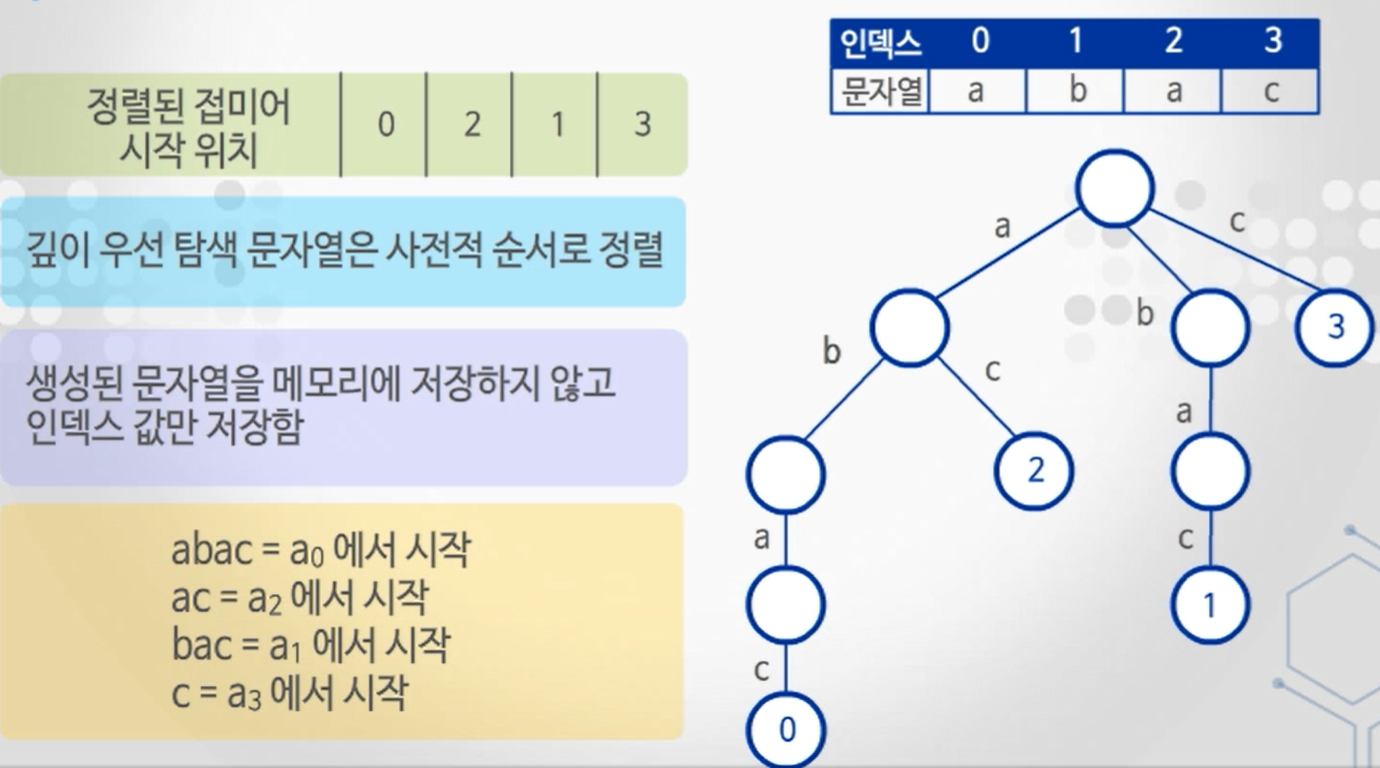
3. 사전적 순서로 정렬된 k번째 접미어 찾기
◾ Compressed 트라이
- 노드들과 간선들을 부분 문자열로 압축
- 하나의 간선이 있을 경우만 압축
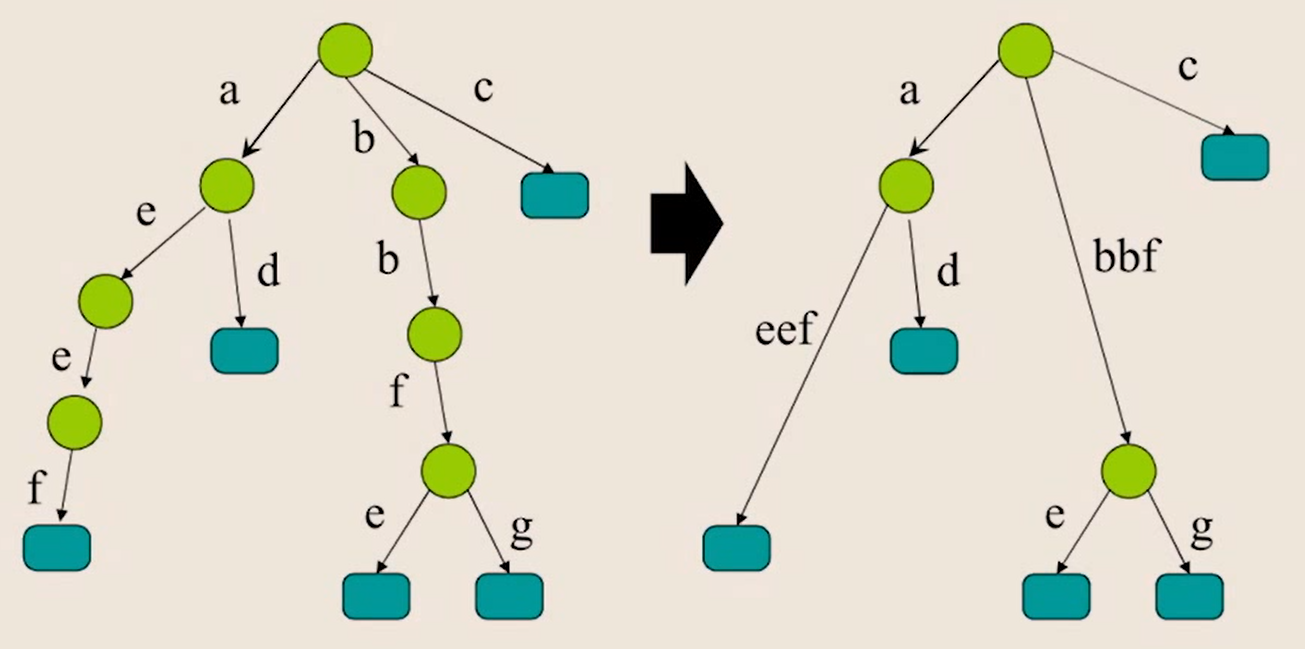
S = { x a b x a }의 접두어
- 1 =
xabxa, 2 =abxa, 3 =bxa, 4 =xa, 5 =a일 때
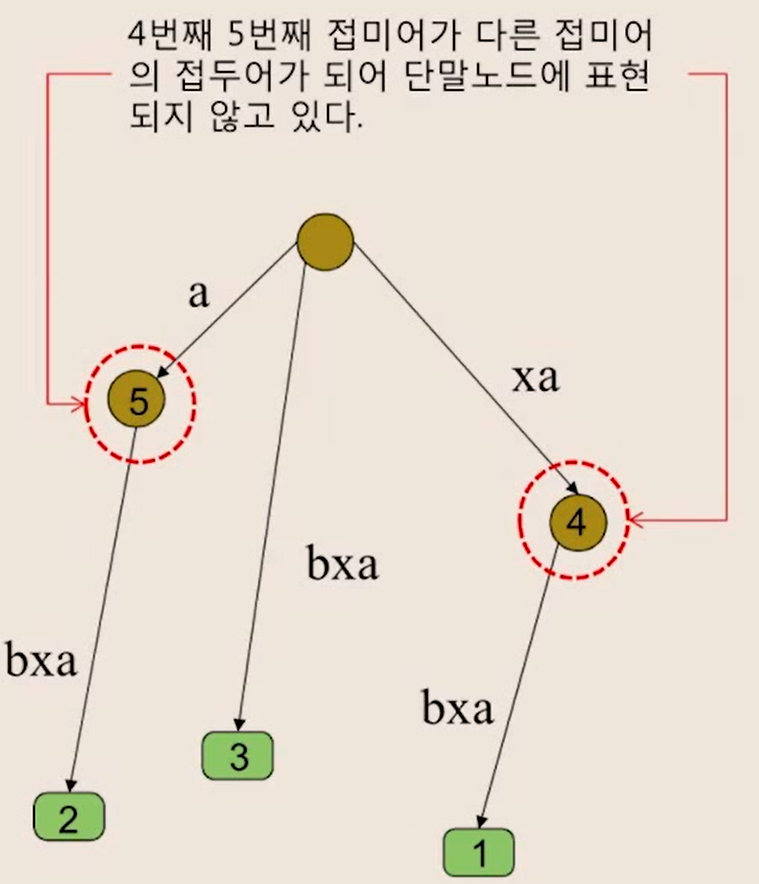
종료 문자($) 추가 : S = { x a b x a $ }의 접두어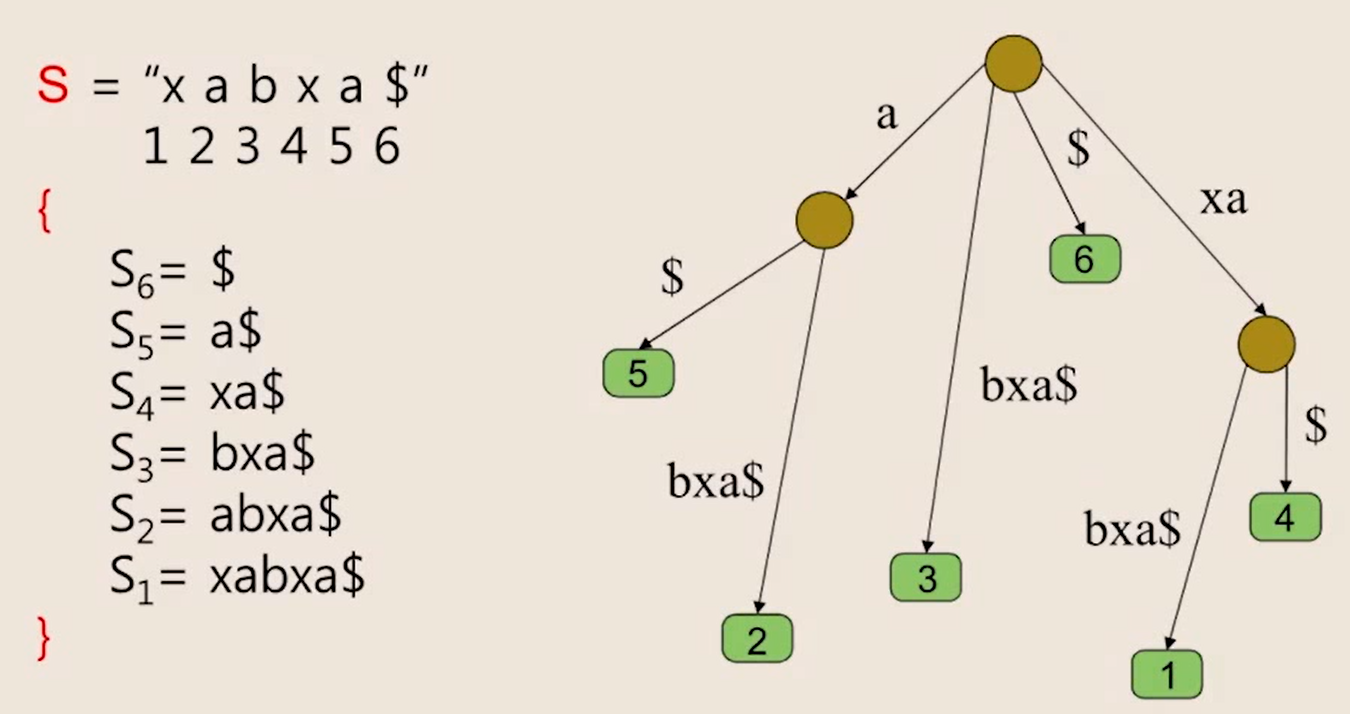
- 하나의 접미어가 다른 접미어의 접두어가 되는 경우를 표현하기 위해 문자열 끝에 특수 문자($) 추가
- 간선 라벨을 효과적으로 저장하기 위해 부분 문자열의 인덱스 시작과 끝(i, j) 저장 가능
◾ 접미어 트리 생성 알고리즘 - Trivial
- 시간 복잡도 : O(n^2)
- 예시
a b a b $
1. 가장 긴 접미어 삽입 후 그 다음 긴 접미어 삽입
- 가장 긴 순서로 삽입
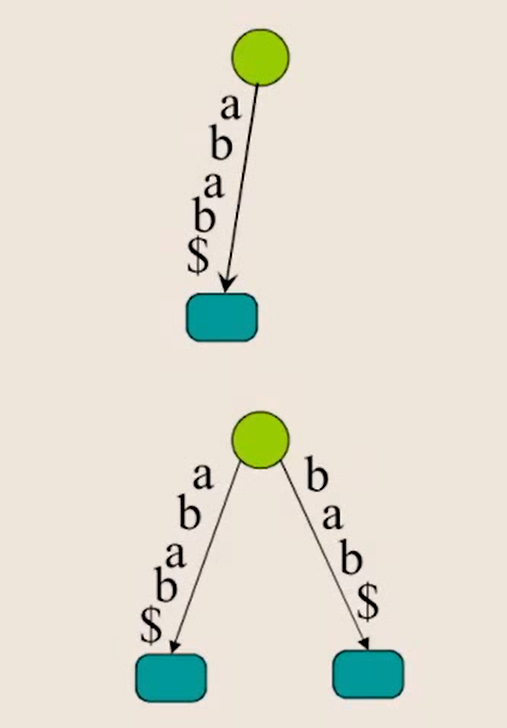
2. 접미어인 ab$ 삽입
- 이때
abab$와 접두어가 공통되어 문자 분리
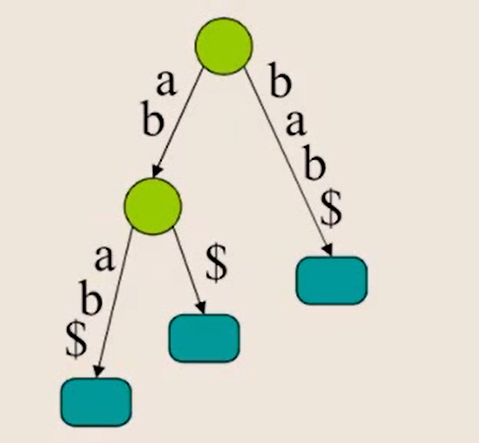
3. b$ 삽입
- 이때 bab$와 접두어가 공통되어 문자 분리
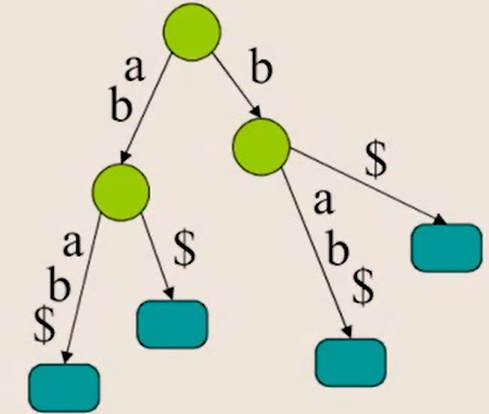
4. 마지막 $(터미널 문자) 삽입
- 종료 문자 삽입
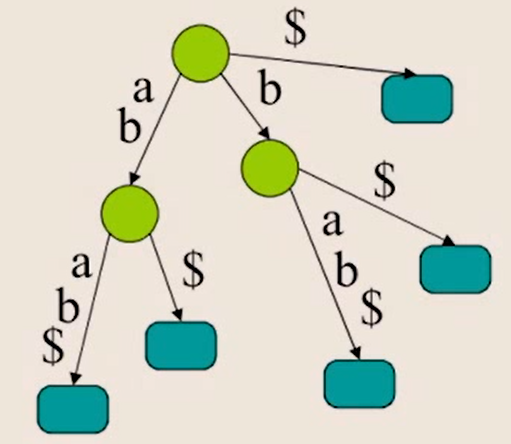
5. 단말 노드 접미어 위치 삽입
- 문자열 순 인덱스 삽입
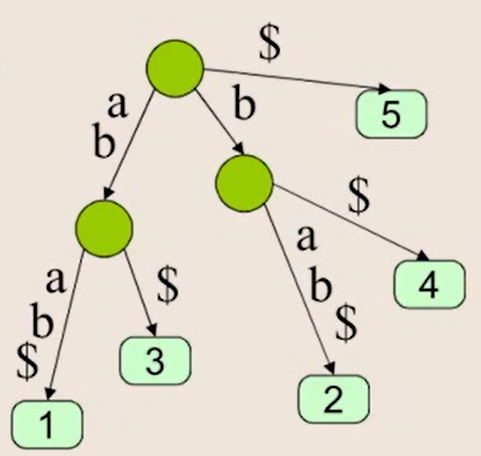
💬 접미어 배열
- 텍스트의 접미어들을 사전순으로 나열한 배열
- 접미어 트리보다 메모리 효율성 높지만 다소 느림
- 텍스트의 인덱싱, 데이터 압축등에 사용
- 공간 복잡도 : O(n)
- 시간 복잡도 : O(패턴 P + log n)
◾ 접미어 배열 생성
- 예시
b a n a n a &
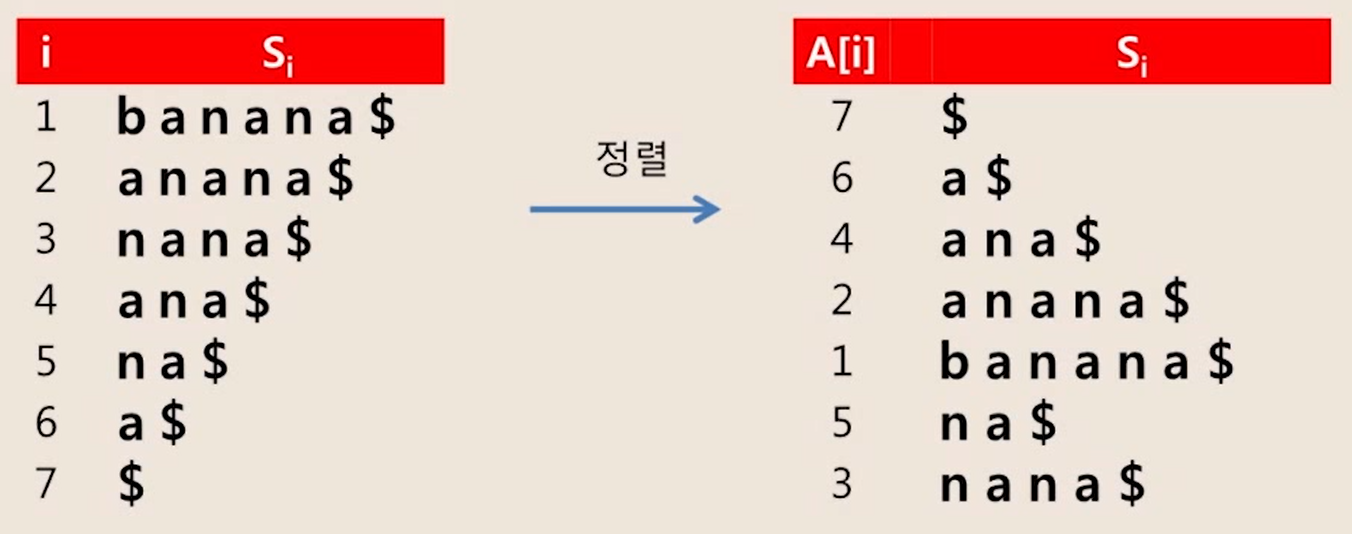
💬 LCP 배열
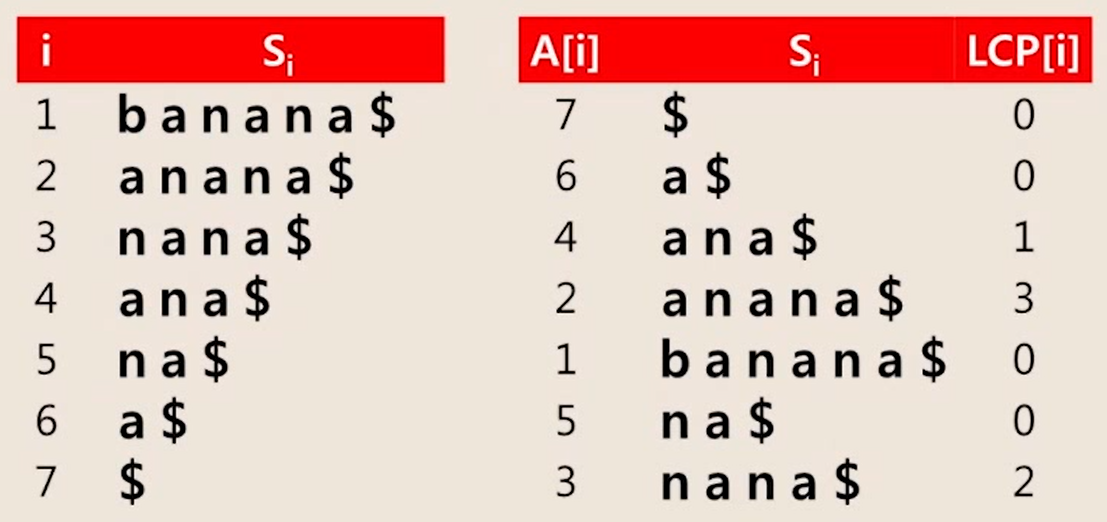
- 접미어 배열의 보조적인 자료 구조로 최장 공통 접두어(LCP) 배열
- 정렬된 접미어 배열에서 연속적인 2개의 접미어들 사이의 최장 공통 접두어의 길이 저장
- 접미어 배열의 순회나 패턴 매칭을 효율적으로 수행
예시
- LCP[4]에서 ana$ 와 anana$ 의 공통 접두어는 ana가 됨