📖 세그먼트 트리

---

정의

• 여러 개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터 합을 구할 때 사용
• 데이터 합을 가장 빠르고 간단하게 구할 수 있는 자료구조

특징

• 고급 자료구조 중 하나
• 시간 복잡도, 공간 복잡도 매우 효율적
• 구현이 짧고, 많은 변형 가능
• 시간 복잡도 : O(log n)

💬 세그먼트 트리 이용 알고리즘

1. 구간합 트리 생성

• 최상단에 전체 원소의 합을 시작으로 구간을 절반씩 분할하며 그 구간의 원소의 합 저장
• 인덱스는 1부터 시작 (2를 곱했을 때 왼쪽 자식 노드를 가리키므로 효과적)
• 재귀적으로 구현하는 게 더 간단
• 트리 배열은 미리 데이터 개수 N에 4를 곱한 크기만큼 미리 할당

	// start: 시작 인덱스, end: 끝 인덱스
    static int init(int[] input, int[] tree, int start, int end, int node) {
        if (start == end)
            return tree[node] = input[start];
        int mid = (start + end) / 2;

        // 병합정렬 늬낌
        return tree[node] = init(input, tree, start, mid, node * 2) // 왼쪽 노드
                + init(input, tree, mid + 1, end, node * 2 + 1);  // 오른쪽 노드
    }

2. 특정 구간 합 구하는 함수

• 시간 복잡도 : O(log n)
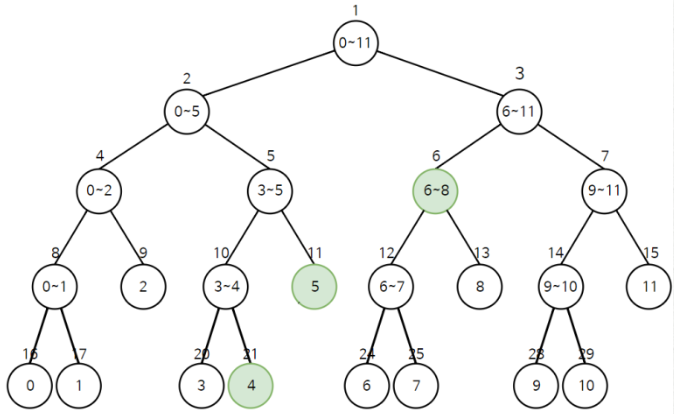
• 4 - 8 인덱스 범위에 대한 합을 구하려면 아래 그림과 같이 세 노드의 합을 구하면 됨
• 구간 합은 범위 안에 있는 경우 한해서 더함
• 재귀적으로 작성하면 간단
  

    // start: 시작 인덱스, end: 끝 인덱스
    // left, right : 구간 범위
    static int sum(int[] input, int[] tree, int start, int end, int node, int left, int right) {
        // 범위 밖인 경우
        if (left > end || right < start)
            return 0;
        // 범위 안인 경우
        if(left <= start && right >= end)
            return tree[node];
        
        // 둘 다 아니면 구간 나누어 합 구하기
        int mid = (start + end) / 2;
        return sum(input, tree, start, mid, node * 2 , left, right)
                + sum(input, tree, mid+1, end, node * 2 + 1, left, right);
    }

3. 특정 원소 값 수정하는 함수

• 특정 원소를 포함하고 있는 모든 구간 합 노드들을 갱신하면 됨
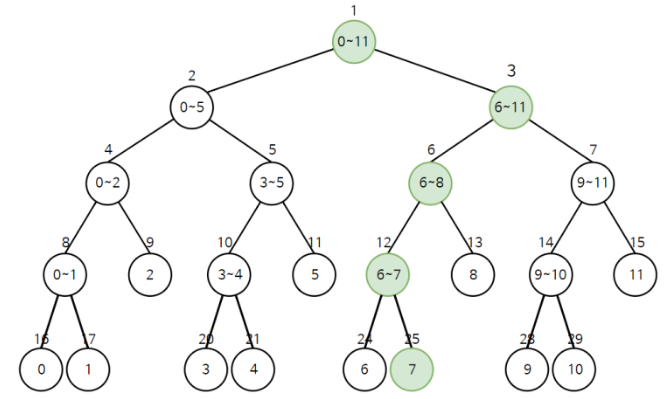
• 예를 들어 인덱스 7 노드를 수정한다면 아래 그림과 같이 5개 구간 합 노드를 모두 수정하면 됨
• 수정할 노드는 범위안에 있는 경우 한해서만 수정
  

    // 특정 원소 값 수정 함수
    // start: 시작 인덱스, end: 끝 인덱스
    // targetIdx: 수정하고자 하는 노드 인덱스
    // val: 수정할 값 
    static void updateTree(int[] input, int[] tree, int start, int end
    	, int node, int targetIdx, int val) {
        // 범위 밖인 경우
        if(targetIdx < start || targetIdx > end)
            return;
        // 범위 안인 경우
        // 내려가며 다른 원소 갱신?
        tree[node] += val;
        if (start == end)
            return;

        int mid = (start + end) / 2;
        updateTree(input, tree, start, mid, node * 2, targetIdx, val);
        updateTree(input, tree, start, mid, node * 2, targetIdx, val);
    }