단순 선형 회귀(Simple Linear Regression)
데이터에 대한 이해(Data Definition)
훈련 데이터셋과 테스트 데이터셋

어떤 학생이 1시간 공부를 했더니 2점,
다른 학생이 2시간 공부를 했더니 4점,
또 다른 학생이 3시간을 공부했더니 6점을 맞았다.
(훈련 데이터셋)
그렇다면 4시간을 공부한다면 몇 점을 맞을 수 있을까?
(테스트 데이터셋)
훈련 데이터셋의 구성
모델을 학습시키기 위한 데이터는 파이토치의 텐서의 형태(torch.tensor)를 가지고 있어야 한다.
x_train은 공부한 시간, y_train은 그에 맵핑되는 점수로 만들어보자.
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])가설(Hypothesis) 수립
선형 회귀란 학습 데이터와 가장 잘 맞는 하나의 직선을 찾는 것이고
이 가설(직선의 방정식)은 y = Wx + b를 가진다.
이 때 x와 곱해지는 W를 가중치(Weight)라고 하며, b를 편향(bias)이라고 한다.
비용 함수(Cost function)에 대한 이해
비용 함수(cost function) = 손실 함수(loss function) = 오차 함수(error function) = 목적 함수(objective function)
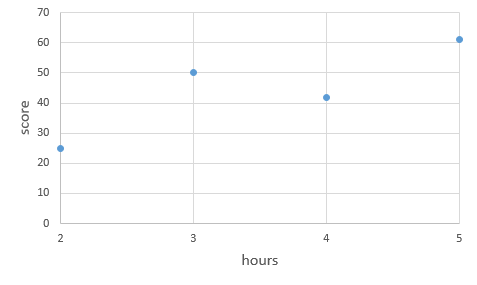
이렇게 4개의 훈련 데이터가 있다고 했을 때, 4개의 점을 잘 표현하는 직선을 찾아보자.
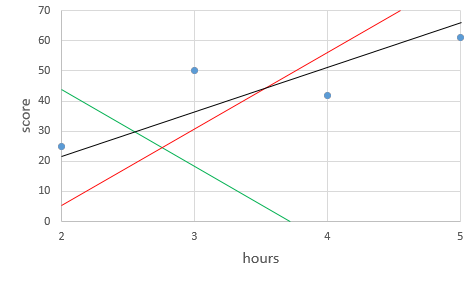
어떻게 찾을 수 있을까?
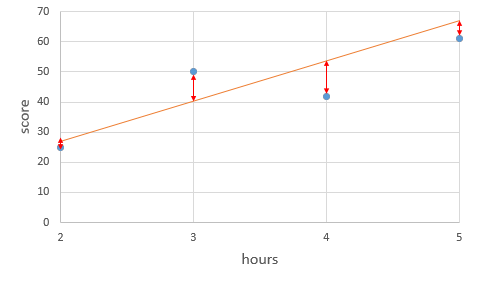
각 실제값과 각 예측값과의 차이를 오차라고 볼 수 있다.
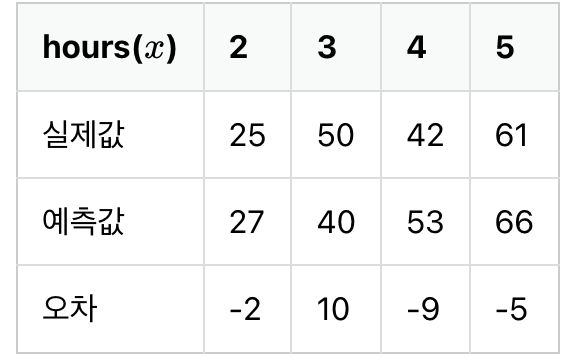
그런데 단순히 '오차 = 실제값 - 예측값'으로 정의하면 오차값이 음수가 나오는 경우가 생긴다.
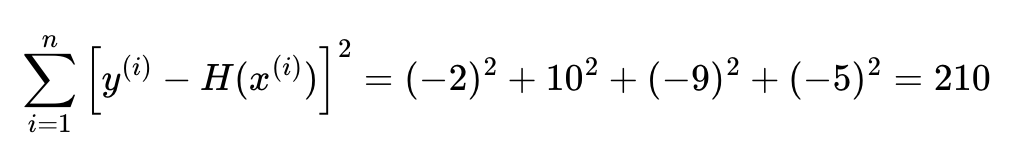
이렇게 오차를 제곱한 후에 더하고
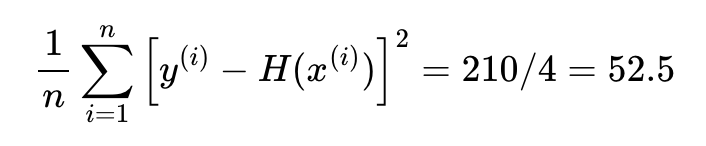
데이터의 개수인 n으로 나누면, 오차의 제곱합에 대한 평균을 구할 수 있는데 이를 평균 제곱 오차(Mean Squared Error, MSE)라고 한다.
평균 제곱 오차를 W와 b에 의한 비용 함수(Cost function)로 재정의하면 아래와 같다.
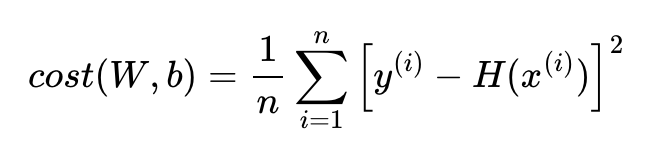
이 때 Cost(W,b)를 최소가 되게 만드는 W,b를 구하는 것이 훈련 데이터를 가장 잘 나타내는 직선을 구하는 것이다.
옵티마이저 - 경사 하강법(Gradient Descent)
그렇다면 이 비용 함수(Cost Function)의 값을 최소로 하는 W,b를 어떻게 찾을 수 있을까?
바로 옵티마이저(최적화 알고리즘)을 사용하는데, 가장 기본적인 옵티마이저인 경사하강법에 대해 알아보자.
b = 0(즉 편향이 0)인 y= Wx을 가정해보자.
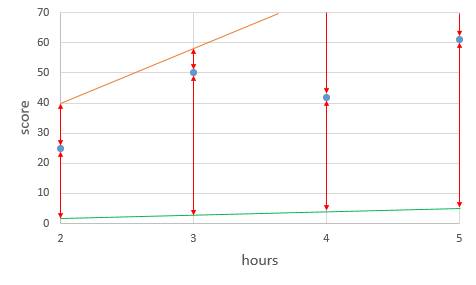
주황색선은 기울기가 20, 초록색선은 기울기가 1이다.
기울기가 지나치게 크면 실제값과 예측값의 오차가 커지고,
기울기가 지나치게 작아도 실제값과 예측값의 오차가 커진다.(b 역시 마찬가지다.)
이 기울기와 cost의 관계를 그래프로 나타내면 다음과 같다.
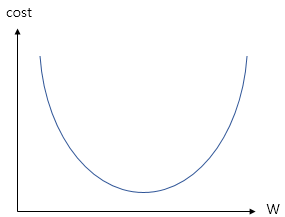
위의 그래프에서 cost가 가장 작은 (최솟값) 부분은 맨 아래의 볼록한 부분,
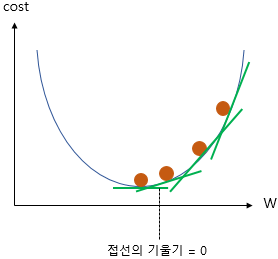
즉 접선의 기울기(미분값)가 0인 부분이다.
경사 하강법의 아이디어는 비용 함수(Cost function)를 미분하여
현재 W에서의 접선의 기울기를 구하고,
접선의 기울기가 낮은 방향으로 W의 값을 변경하는 작업을 반복하는 것이다.
이 반복 작업에는 현재 W에 접선의 기울기를 구해 특정 숫자 α를 곱한 값을 빼서 새로운
W로 사용하는 식이 사용된다.
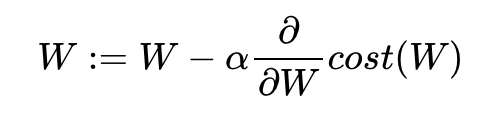
이 때 기울기가 양수이면 W값이 감소하고, 기울기가 음수이면 W값이 증가한다.
여기서 a(학습률)은 W을 변경할 때 얼마나 크게 변경할지를 결정한다.
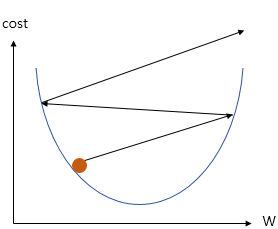
학습률 a이 너무 커도 너무 작아도 안되고, 적당한 값을 찾아야한다.
파이토치로 선형 회귀 구현하기
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optimx_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])이제 가장 잘 맞는 직선을 정의하는 W,b값을 찾아보자.
우선 가중치 W를 0으로 초기화하고, 이 값을 출력해보자.
# 가중치 W를 0으로 초기화하고 학습을 통해 값이 변경되는 변수임을 명시함.
W = torch.zeros(1, requires_grad=True)
# 가중치 W를 출력
print(W) #tensor([0.], requires_grad=True)여기서 requires_grad=True는 학습을 통해 계속 값이 변경되는 변수임을 의미한다.
편향 b도 0으로 초기화하고, 학습을 통해 값이 변경되는 변수임을 명시하자.
b = torch.zeros(1, requires_grad=True)
print(b) #tensor([0.], requires_grad=True)현재는 W,b모두 0이므로 y = 0 * x + 0이다. 즉 어떤 x값에도 0을 예측한다.
그렇다면 이제 직선의 방정식에 해당되는 가설을 선언해보자.
hypothesis = x_train * W + b
print(hypothesis)이제 비용함수에 해당되는 평균 제곱 오차를 선언해보자.
cost = torch.mean((hypothesis - y_train) ** 2)
print(cost) #tensor(18.6667, grad_fn=<MeanBackward0>)이제 경사하강법을 구현해보자.
SGD는 경사하강법의 일종이고, lr은 학습률을 의미한다.
optimizer = optim.SGD([W, b], lr=0.01)optimizer.zero_grad()은 미분을 통해 얻은 기울기를 0으로 초기화한다.
기울기를 초기화해야만 새로운 가중치 편향에 대해서 새로운 기울기를 구할 수 있다.
cost.backward() 함수를 호출하면 가중치 W와 편향 b에 대한 기울기가 계산된다.
그 다음 경사 하강법 최적화 함수 opimizer의 .step() 함수를 호출하여 인수로 들어갔던 W와 b에서 리턴되는 변수들의 기울기에 학습률(learining rate) 0.01을 곱하여 빼줌으로서 업데이트한다.
전체코드
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)
nb_epochs = 1999 # 원하는만큼 경사 하강법을 반복
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))에포크(Epoch)는 학습량으로 위 코드에서는 2,000번을 수행했다.
최종 훈련 결과에서 최적의 기울기 W는 2에 가깝고 b는 0에 가깝다.
optimizer.zero_grad()가 필요한 이유
파이토치는 미분을 통해 얻은 기울기를 이전에 계산된 기울기 값에 누적시키는 특징이 있다.
import torch
w = torch.tensor(2.0, requires_grad=True)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
z = 2*w
z.backward()
print('수식을 w로 미분한 값 : {}'.format(w.grad))이 코드를 실행해보면 계속 미분값 2가 누적된다.그래서 optimizer.zero_grad()를 통해 미분값을 계속 0으로 초기화시켜야 한다.
torch.manual_seed()를 하는 이유
torch.manual_seed()를 사용한 프로그램의 결과는 다른 컴퓨터에서 실행시켜도 동일한 결과를 얻을 수 있다. 난수 발생 순서와 값을 동일하게 보장해주기 때문이다.
torch.manual_seed(3)
print('랜덤 시드가 3일 때')
for i in range(1,3):
print(torch.rand(1))랜덤 시드가 3일 때
tensor([0.0043])
tensor([0.1056])랜덤시드를 바꿔보자.
torch.manual_seed(5)
print('랜덤 시드가 5일 때')
for i in range(1,3):
print(torch.rand(1))랜덤 시드가 5일 때
tensor([0.8303])
tensor([0.1261])다시 3으로 바꿔보자.
torch.manual_seed(3)
print('랜덤 시드가 다시 3일 때')
for i in range(1,3):
print(torch.rand(1))다시 동일하게 나온다.
자동 미분(Autograd)
값이 2인 임의의 스칼라 텐서 w를 선언하고, required_grad를 True로 설정하자
(텐서에 대한 기울기를 저장하겠다는 의미).
w = torch.tensor(2.0, requires_grad=True)이제 수식을 정의하고 해당 수식을 w에 대해 미분하자.
y = w**2
z = 2*y + 5
z.backward()print('수식을 w로 미분한 값 : {}'.format(w.grad)) #수식을 w로 미분한 값 : 8.0다중 선형 회귀(Multivariable Linear regression)
위의 x가 1개인 회귀를 단순 선형 회귀(Simple Linear Regression)라고 한다.
이번엔 다수의 x로부터 y를 예측하는 다중 선형 회귀(Multivariable Linear Regression)를 알아보자.
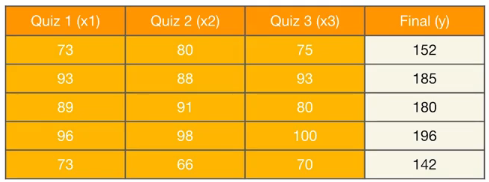
3개의 퀴즈 점수로부터 최종 점수를 예측하는 모델을 만들어보자.
독립변수 x의 개수가 3개므로 이를 수식으로 표현하면 아래와 같다.
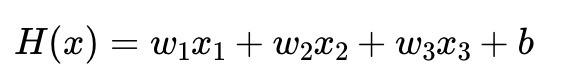
랜덤시드를 1로 고정하고 실습해보자
torch.manual_seed(1)# 훈련 데이터
x1_train = torch.FloatTensor([[73], [93], [89], [96], [73]])
x2_train = torch.FloatTensor([[80], [88], [91], [98], [66]])
x3_train = torch.FloatTensor([[75], [93], [90], [100], [70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])# 가중치 w와 편향 b 초기화
w1 = torch.zeros(1, requires_grad=True)
w2 = torch.zeros(1, requires_grad=True)
w3 = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)# optimizer 설정
optimizer = optim.SGD([w1, w2, w3, b], lr=1e-5)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x1_train * w1 + x2_train * w2 + x3_train * w3 + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} w1: {:.3f} w2: {:.3f} w3: {:.3f} b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, w1.item(), w2.item(), w3.item(), b.item(), cost.item()
))그런데 선형대수학에서 배웠던 행렬곱을 이용해 위의 식을 표현할 수도 있다.
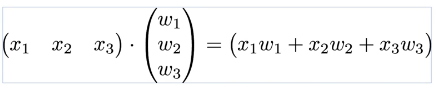
즉
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 80],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])x_train 하나에 모든 샘플을 전부 선언하여 다시 말해 (5 x 3) 행렬 x_train을 선언하였다.
# 가중치와 편향 선언
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)X_train의 행렬의 크기는 (5 × 3)이므로, 가중치 W는 행렬곱이 가능하다.
hypothesis = x_train.matmul(W) + b전체코드를 보자.
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 80],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# 모델 초기화
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
# H(x) 계산
# 편향 b는 브로드 캐스팅되어 각 샘플에 더해집니다.
hypothesis = x_train.matmul(W) + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
epoch, nb_epochs, hypothesis.squeeze().detach(), cost.item()
))nn.Module로 구현하는 선형 회귀
위에서는 가설, 비용 함수를 직접 정의해서 선형 회귀 모델을 구현했는데
이제 파이토치에서 이미 구현되어져 제공되고 있는 함수들을 불러와 더 쉽게 선형 회귀 모델을 구현해보자.
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(1)단순 선형 회귀 구현하기
아래의 데이터는 y=2x에서 x,y의 값들이다.(우리는 w = 2, b = 0임을 알고 있다.)
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])nn.Linear()는 입력의 차원, 출력의 차원을 인수로 받는다.
# 모델을 선언 및 초기화. 단순 선형 회귀이므로 input_dim=1, output_dim=1.
model = nn.Linear(1,1)하나의 입력 x에 대해서 하나의 출력 y을 가지므로, 입력 차원과 출력 차원 모두 1을 인수로 사용한다.
model에는 가중치 W와 편향 b가 저장되어있는데, 이 값은 model.parameters()라는 함수를 사용하여 불러올 수 있다.
print(list(model.parameters()))
# [Parameter containing:
# tensor([[0.5153]], requires_grad=True), Parameter containing:
# tensor([-0.4414], requires_grad=True)]이 때 첫번째 값이 W, 두번째 값이 b이다.(랜덤 초기화된 값)
이제 옵티마이저를 정의해보자. model.parameters()를 사용하여 W와 b를 전달하고 lr을 0.01로 정하자.
# optimizer 설정. 경사 하강법 SGD를 사용하고 learning rate를 의미하는 lr은 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) 전체코드
# 전체 훈련 데이터에 대해 경사 하강법을 2,000회 반복
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward() # backward 연산
# W와 b를 업데이트
optimizer.step()
if epoch % 100 == 0:
# 100번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))# 임의의 입력 4를 선언
new_var = torch.FloatTensor([[4.0]])
# 입력한 값 4에 대해서 예측값 y를 리턴받아서 pred_y에 저장
pred_y = model(new_var) # forward 연산
# y = 2x 이므로 입력이 4라면 y가 8에 가까운 값이 나와야 제대로 학습이 된 것
print("훈련 후 입력이 4일 때의 예측값 :", pred_y) 훈련 후 입력이 4일 때의 예측값 : tensor([[7.9989]], grad_fn=<AddmmBackward0>)8에 가까운 값이 나왔다.
이제 학습 후의 W와 b의 값을 출력해보자.
print(list(model.parameters()))[Parameter containing:
tensor([[1.9994]], requires_grad=True), Parameter containing:
tensor([0.0014], requires_grad=True)]다중 선형 회귀 구현하기
3개의 x로부터 하나의 y를 예측해보자.
ㅁ
# 데이터
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])# 모델을 선언 및 초기화. 다중 선형 회귀이므로 input_dim=3, output_dim=1.
model = nn.Linear(3,1)torch.nn.Linear 인자로 3, 1을 사용하였다. 즉
3개의 입력 x에 대해서 하나의 출력 y을 가지므로,
입력 차원은 3, 출력 차원은 1이다.
model에는 3개의 가중치 w와 편향 b가 저장되어있는데, 확인해보자.
print(list(model.parameters()))[Parameter containing:
tensor([[ 0.2975, -0.2548, -0.1119]], requires_grad=True), Parameter containing:
tensor([0.2710], requires_grad=True)]첫번째 출력되는 것이 3개의 w고, 두번째 출력되는 것이 b이다.(랜덤 초기화된 값)
옵티마이저를 정의해보자.
model.parameters()를 사용하여 3개의 w와 b를 전달하고, lr은 0.00001로 정하자.
(lr을 0.01로 하니 발산하여 cost가 nan으로 나왔다)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5) nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# model(x_train)은 model.forward(x_train)와 동일함.
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward()
# W와 b를 업데이트
optimizer.step()
if epoch % 100 == 0:
# 100번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))x에 임의의 입력 [73, 80, 75]를 넣어 모델이 예측하는 y의 값을 확인해보자
(그런데 사실 앞에서 훈련 데이터로 사용했었다)
# 임의의 입력 [73, 80, 75]를 선언
new_var = torch.FloatTensor([[73, 80, 75]])
# 입력한 값 [73, 80, 75]에 대해서 예측값 y를 리턴받아서 pred_y에 저장
pred_y = model(new_var)
print("훈련 후 입력이 73, 80, 75일 때의 예측값 :", pred_y) 훈련 후 입력이 73, 80, 75일 때의 예측값 : tensor([[152.9719]], grad_fn=<AddmmBackward0>)대략 비슷하게 나온다.
학습 후의 3개의 w와 b의 값을 출력해보자.
print(list(model.parameters()))[Parameter containing:
tensor([[0.6294, 0.6883, 0.6936]], requires_grad=True), Parameter containing:
tensor([-0.0603], requires_grad=True)]클래스로 파이토치 모델 구현하기
보통 대부분 모델을 생성할 때 클래스를 사용한다.
앞에서 단순 선형 회귀 모델은 다음과 같이 구현했었다.
# 모델을 선언 및 초기화. 단순 선형 회귀이므로 input_dim=1, output_dim=1.
model = nn.Linear(1,1)이를 클래스로 구현하면 다음과 같다.
class LinearRegressionModel(nn.Module): # torch.nn.Module을 상속받는 파이썬 클래스
def __init__(self): #
super().__init__()
self.linear = nn.Linear(1, 1) # 단순 선형 회귀이므로 input_dim=1, output_dim=1.
def forward(self, x):
return self.linear(x)
model = LinearRegressionModel()또 다중 선형 회귀 모델은 다음과 같이 구현했었다.
# 모델을 선언 및 초기화. 다중 선형 회귀이므로 input_dim=3, output_dim=1.
model = nn.Linear(3,1)이는 클래스로 다음과 같다.
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1) # 다중 선형 회귀이므로 input_dim=3, output_dim=1.
def forward(self, x):
return self.linear(x)
model = MultivariateLinearRegressionModel()클래스 형태의 모델은 nn.Module 을 상속받고
__init__()에서 모델의 구조와 동작을 정의하는 생성자를 정의한다.(객체가 생성될 때 자동으호 호출)
super() 함수를 부르면 여기서 만든 클래스는 nn.Module 클래스의 속성들을 가지고 초기화된다.
foward() 함수는 모델이 학습데이터를 입력받아서 forward 연산을 진행시키는 함수로, model 객체를 데이터와 함께 호출하면 자동으로 실행된다.
단순 선형 회귀 클래스로 구현하기
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
class LinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
model = LinearRegressionModel()
# optimizer 설정. 경사 하강법 SGD를 사용하고 learning rate를 의미하는 lr은 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 전체 훈련 데이터에 대해 경사 하강법을 2,000회 반복
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward() # backward 연산
# W와 b를 업데이트
optimizer.step()
if epoch % 100 == 0:
# 100번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))다중 선형 회귀 클래스로 구현하기
# 데이터
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1) # 다중 선형 회귀이므로 input_dim=3, output_dim=1.
def forward(self, x):
return self.linear(x)
model = MultivariateLinearRegressionModel()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5)
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# model(x_train)은 model.forward(x_train)와 동일함.
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward()
# W와 b를 업데이트
optimizer.step()
if epoch % 100 == 0:
# 100번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))미니 배치와 데이터 로드(Mini Batch and Data Load)
미니 배치와 배치 크기(Mini Batch and Batch Size)
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])위 데이터의 샘플의 개수는 5개이고, 경사하강법을 수행하여 쉽게 학습할 수 있었지만
만약 데이터가 수십만개 이상이라면 전체 데이터에 대해서 경사 하강법을 수행하는 것은 매우 느릴 뿐만 아니라 많은 계산량이 필요하다.
그래서 전체 데이터를 더 작은 단위로 나누어서 해당 단위로 학습하고,
이 단위를 미니 배치(Mini Batch)라고 한다.
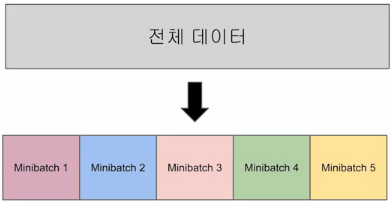
미니 배치 학습을 하게되면 미니 배치만큼만 가져가서 미니 배치에 대한 대한 비용(cost)를 계산하고, 경사 하강법을 수행한다.
그리고 다음 미니 배치를 가져가서 경사 하강법을 수행하고 마지막 미니 배치까지 이를 반복합니다. 이렇게 전체 데이터에 대한 학습이 1회 끝나면 1 에포크(Epoch)가 끝난다.
즉 미니 배치의 개수만큼 경사 하강법을 수행해야 전체 데이터가 한 번 전부 사용되어 1 에포크(Epoch)가 된다.
보통 배치 크기는 보통 2의 제곱수를 사용합하는데 그 이유는 CPU와 GPU의 메모리가 2의 배수이므로 배치크기가 2의 제곱수일 경우에 데이터 송수신의 효율을 높일 수 있기 때문이다.
이터레이션(Iteration)
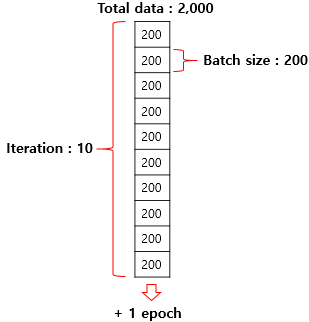
이터레이션은 한 번의 에포크 내에서 이루어지는 매개변수인 w,b의 업데이트 횟수이다.
전체 데이터가 2,000일 때 배치 크기를 200으로 한다면 이터레이션의 수는 총 10개이다.
이는 한 번의 에포크 당 매개변수 업데이트가 10번 이루어진다는 뜻이다.
데이터 로드하기(Data Load)
파이토치는 데이터를 좀 더 쉽게 다루기 위한 데이터셋(Dataset)과 데이터로더(DataLoader)를 제공하는데
이를 사용하면 미니 배치 학습, 데이터 셔플(shuffle), 병렬 처리까지 간단히 수행할 수 있다.
본적인 사용 방법은 Dataset을 정의하고, 이를 DataLoader에 전달하는 것이다.
from torch.utils.data import TensorDataset # 텐서데이터셋
from torch.utils.data import DataLoader # 데이터로더TensorDataset은 기본적으로 텐서를 입력으로 받는다. (텐서 형태로 데이터를 정의)
이를 TensorDataset의 입력으로 사용하고 dataset으로 저장한다.
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
dataset = TensorDataset(x_train, y_train)파이토치의 데이터셋을 만들었다면 데이터로더를 사용할 수 있다.
데이터로더는 기본적으로 2개의 인자(데이터셋, 미니 배치의 크기)를 입력받는다.
또 추가적으로 많이 사용되는 인자로 shuffle이 있는데, shuffle=True를 선택하면 Epoch마다 데이터셋을 섞어서 데이터가 학습되는 순서를 바꾼다.
모델이 데이터셋의 순서에 익숙해지는 것을 방지하여 학습할 때는 이 옵션을 True를 주는 것을 권장한다.
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)이제 모델과 옵티마이저를 설계하고 훈련을 시켜보자.
model = nn.Linear(3,1)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5) nb_epochs = 20
for epoch in range(nb_epochs + 1):
for batch_idx, samples in enumerate(dataloader):
# print(batch_idx)
# print(samples)
x_train, y_train = samples
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train)
# cost로 H(x) 계산
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} Batch {}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, batch_idx+1, len(dataloader),
cost.item()
))실행해보면 Cost의 값이 점차 작아진다. 모델의 입력으로 임의의 값을 넣어 예측값을 확인해보자.
# 임의의 입력 [73, 80, 75]를 선언
new_var = torch.FloatTensor([[73, 80, 75]])
# 입력한 값 [73, 80, 75]에 대해서 예측값 y를 리턴받아서 pred_y에 저장
pred_y = model(new_var)
print("훈련 후 입력이 73, 80, 75일 때의 예측값 :", pred_y) 커스텀 데이터셋(Custom Dataset)
torch.utils.data.Dataset을 상속받아 직접 커스텀 데이터셋(Custom Dataset)을 만들 수도 있다.
torch.utils.data.Dataset은 파이토치에서 데이터셋을 제공하는 추상 클래스이다.
class CustomDataset(torch.utils.data.Dataset):
def __init__(self):
데이터셋의 전처리를 해주는 부분
def __len__(self):
데이터셋의 길이. 즉, 총 샘플의 수를 적어주는 부분
def __getitem__(self, idx):
데이터셋에서 특정 1개의 샘플을 가져오는 함수커스텀 데이터셋(Custom Dataset)으로 선형 회귀 구현하기
import torch
import torch.nn.functional as F
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
# Dataset 상속
class CustomDataset(Dataset):
def __init__(self):
self.x_data = [[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]]
self.y_data = [[152], [185], [180], [196], [142]]
# 총 데이터의 개수를 리턴
def __len__(self):
return len(self.x_data)
# 인덱스를 입력받아 그에 맵핑되는 입출력 데이터를 파이토치의 Tensor 형태로 리턴
def __getitem__(self, idx):
x = torch.FloatTensor(self.x_data[idx])
y = torch.FloatTensor(self.y_data[idx])
return x, ydataset = CustomDataset()
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)
model = torch.nn.Linear(3,1)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
for batch_idx, samples in enumerate(dataloader):
# print(batch_idx)
# print(samples)
x_train, y_train = samples
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train)
# cost로 H(x) 계산
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} Batch {}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, batch_idx+1, len(dataloader),
cost.item()
))
