
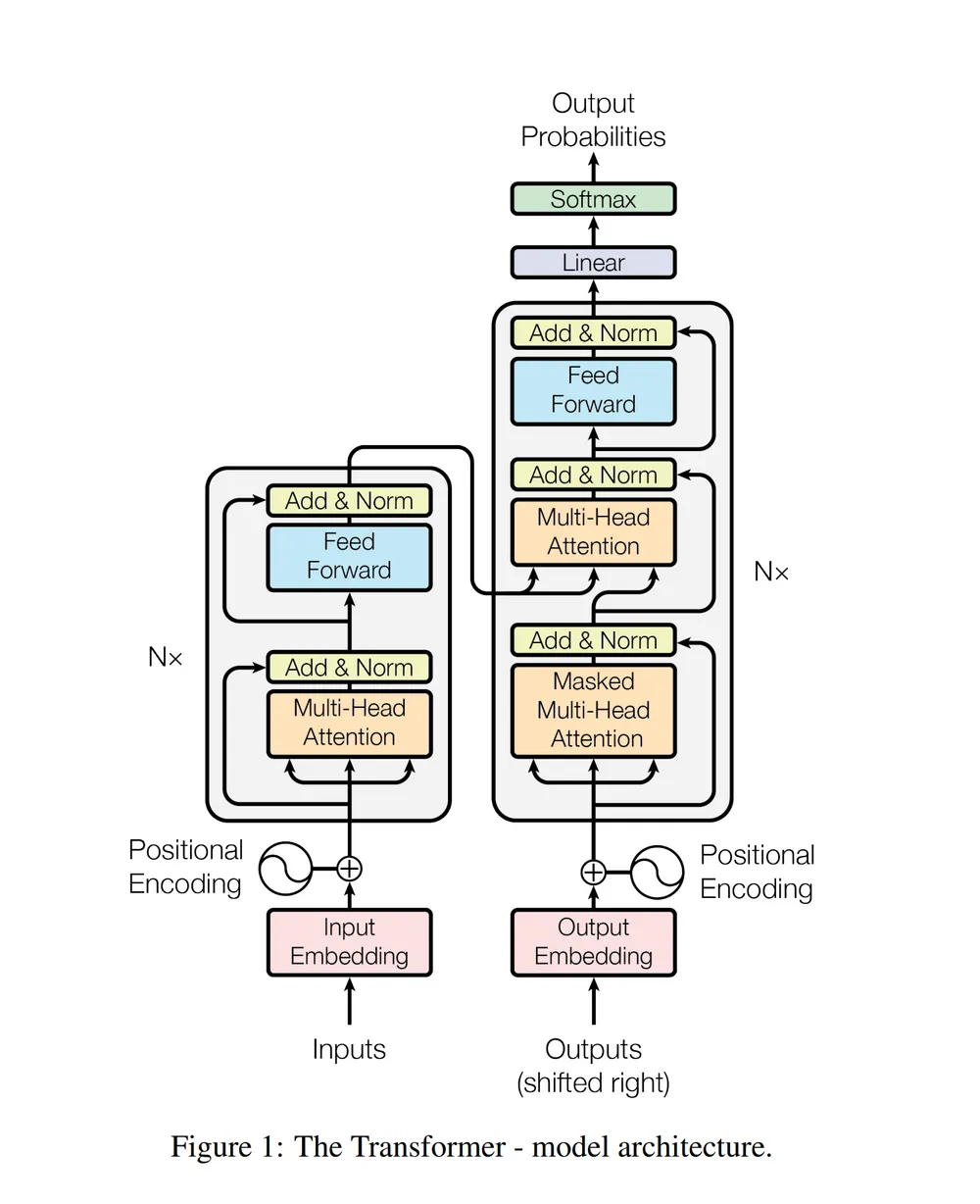
이전 게시글에서는 positional encoding에 대해 설명했다. 이제 얼마 안남았다 아자아자 안화이팅.
킹무튼 위의 트랜스포머 아키텍처에 따르면, positional encoding까지 더해진 input vector들은 encoder block의 sub-layer를 지나가게 된다.
(이 sub-layer는 multi-head attention과 feed forward nerural network이다.)
multihead-self attention에 대해 이해하기 위해서 self-attention에 대한 이해가 먼저 필요하다.
스포하자면, Self-Attention이란 입력 시퀀스 내의 각 단어가 다른 모든 단어들과의 연관성을 계산하는 것이고,
Multi-Head Attention은 여러 개의 독립적인 self-attention 메커니즘을 병렬로 적용하여 다양한 표현 학습하는 것이다.
Self-attention
- The animal didn’t cross the street because it was too tired 라는 문장을 보자. 우리는 it이 뭔지 알지만 신경망 모델에게는 간단하지 않다.
- 트랜스포머 모델은 it을 처리할 때 self-attention을 이용해 it과 animal을 연결할 수 있다.

- 모델이 input sequence의 각 단어를 처리해 나감에 따라, self-attention은 input sequence 내의 다른 위치에 있는 단어들을 보고 거기서 힌트를 받아 현재 타겟 위치의 단어를 더 잘 encoding 할 수 있다.
그래서 결론적으로 어떻게 self-attention 을 계산하는 것일까?
1. Query,Key,Value 벡터 변환
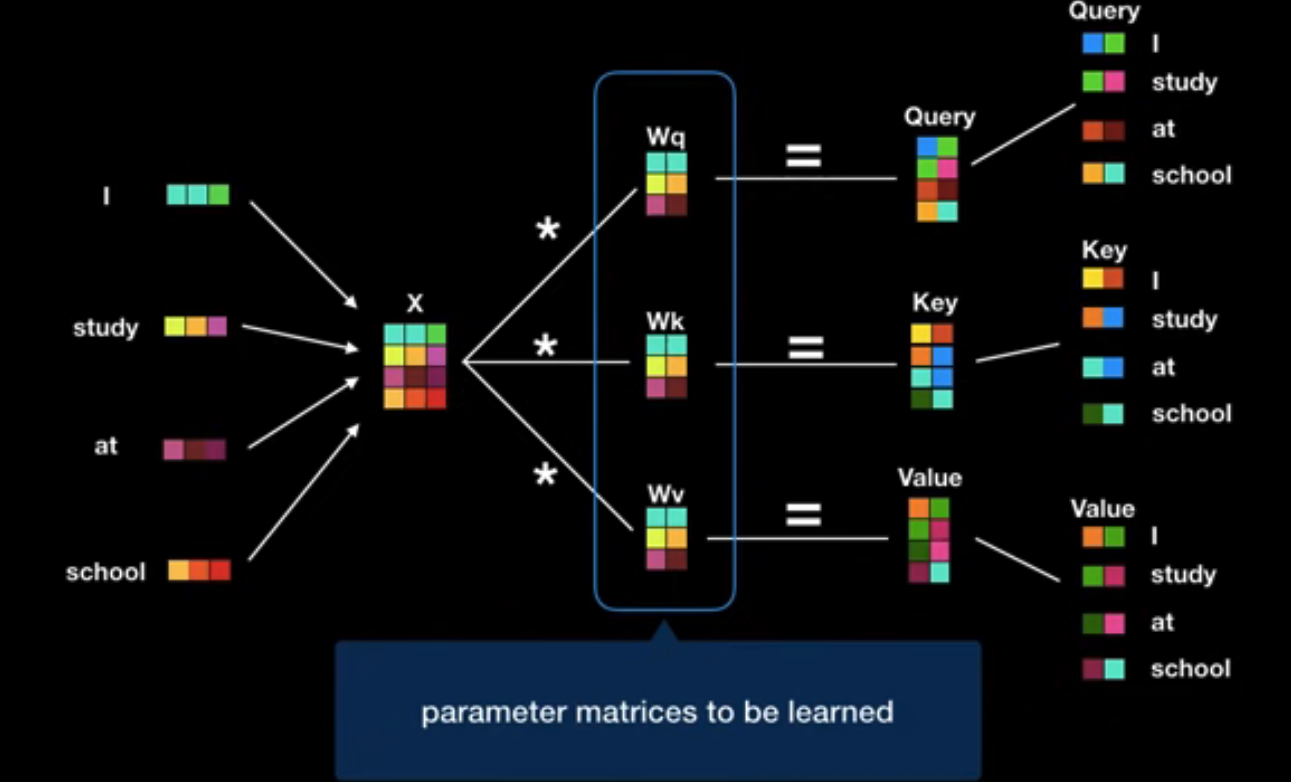
우선 입력 시퀀스의 각 단어를 Query, Key, Value 벡터로 변환한다.
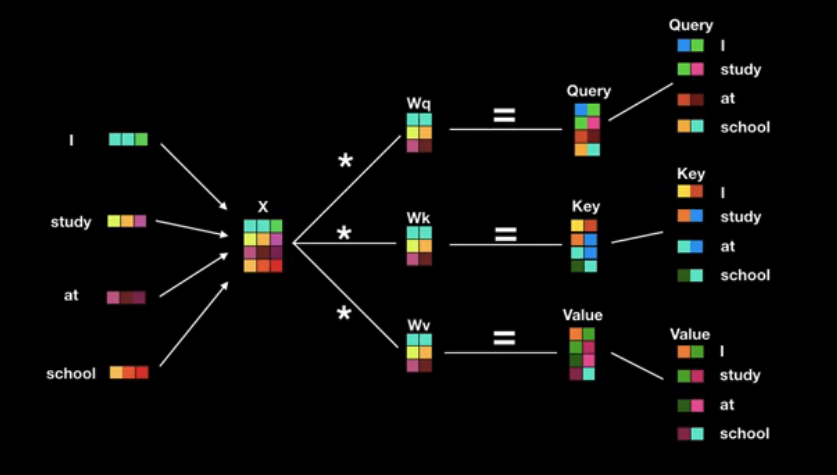
이 Query,Key,Value 3가지 벡터는 ( 행렬에 대해 생성되는데,
이 행렬은 weight matrix로서 학습과정에서 최적화된다.
- Query: 현재 보고있는 current word의 representation으로, 다른 단어들과 scoring을 하기위해 기준이 되는 값(물어볼 주체)
- Key: Query와 attention을 수행할 단어들
- Value: 실제 actual word representation(실제 값)
(Query, Key, Value는 벡터의 형태라는 것을 꼭 기억하자.)
2. Scaled Dot-Product Attention 계산
Query, Key, Value를 구한 이후, Scaled Dot-Product Attention 연산을 거치는데,
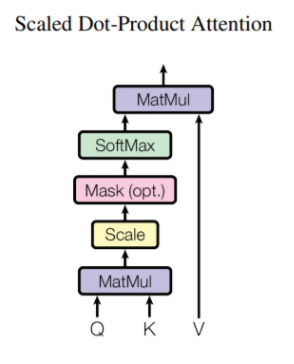

(위 사진에서 softmax에 설명이 생략되었는데,
softmax를 실행하기 전에 score를 키 벡터의 차원 수의 루트값 나눈다)
- 각 토큰 i에서, input token x_i는 3개의 가중치 행렬(과 곱해서, Query,Key,Value 벡터를 생성한다.
- 즉 Query vector , key vector , value vector
- Attention score는 Query,Key 벡터를 통해 계산된다. 예를 들어 토큰 i에서 j로 가는 attention score 는 사이의 dot product이다.
- attention score는 key vector 차원의 제곱근으로 나뉘어고, 는 훈련 중 기울기를 안정화시키고, softmax를 통과한다.(softmax의 결과값은 key값에 해당하는 단어가 현재 단어에 어느정도 연관성이 있는지를 나타낸다. )
이를 Scaled Dot-Product Attention이라고 한다.
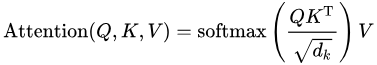
어렵다. 더 디테일하게 보도록 하자..
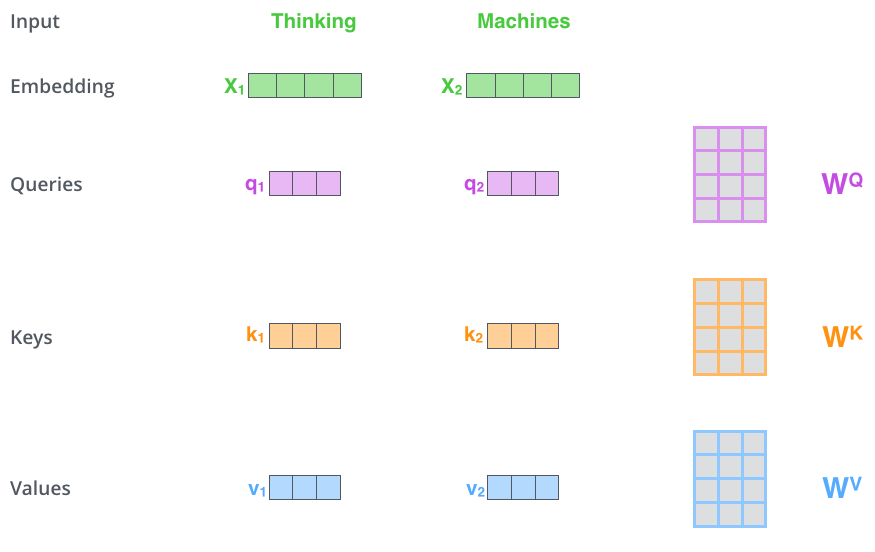
-
Thinking machines 라는 문장이 있고, 임베딩 벡터를 라고 하자,
-
학습과정에서 최적화되는 weight matrix ( 와 각 단어 을 곱해서 Query,Key,Value 벡터를 생성한다.
2.1 현재 단어와 연관된 Query vector인 이고,
쿼리벡터와 scoring을 하기 위한 다른 위치에 있는 key vector인 이고,
실제 단어 값 value vector는 이다.
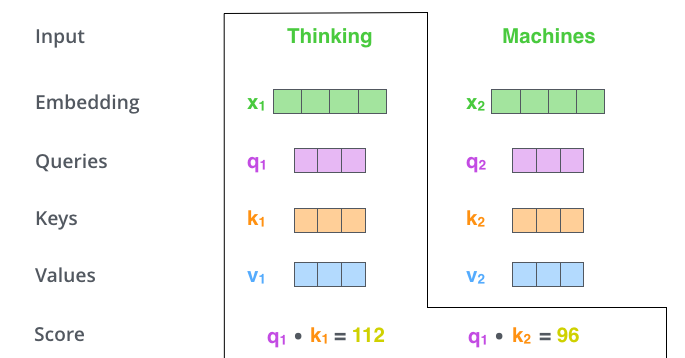
- 현재 단어의 query vector와 점수를 매기려 하는 다른 위치에 있는 단어의 key vector의 내적으로 score를 계산하자.(현재 단어의 self attention)
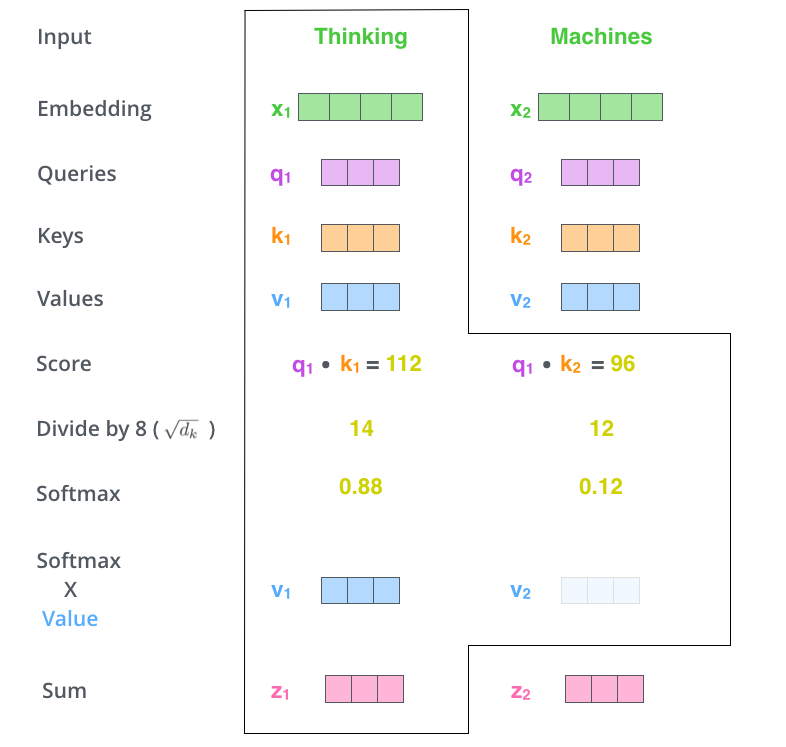
-
그리고 차원의 루트개수만큼 나눈다.(query,key,value가 64차원이기 때문에 8차원) 이를 통해 더 안정적인 그라디언트를 가질 수 있다.
-
그 이후 softmax를 취한다. (현재 포지션의 단어와 내가 보고있는 단어와 얼마나 중요한가를 의미)
-
그 softmax값과 value값을 곱한다. 이 출력이 바로 현재 위치에 대한 self-attention layer의 출력이다.
Multi-head Attention
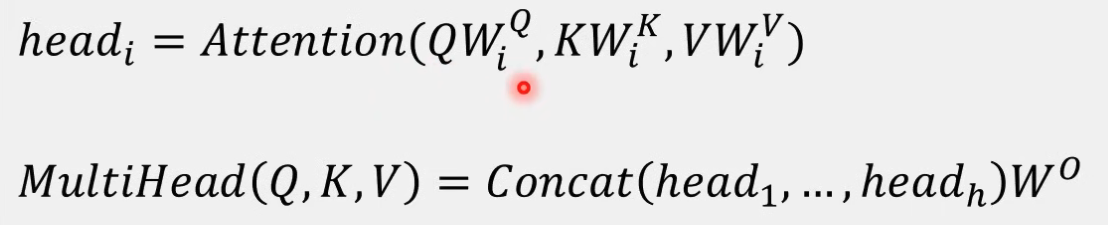
- 이 논문에서는 self-attention layer에다 “multi-head” attention이라는 메커니즘을 더해서 성능을 향상시키는데,
- Multi-head Attention은 위의 self-attention을 여러개 이용하는 것이다.
- ( 집합을 attention head라고 하는데, 트랜스포머의 각 레이어에는 여러 attention head(본 논문에서는 8개)를 가지고 있다.
- 이 attention head가 i로 인덱싱 된다고 하면 multi-head attention은 다음과 같다.
어렵다.. 다시 보자..
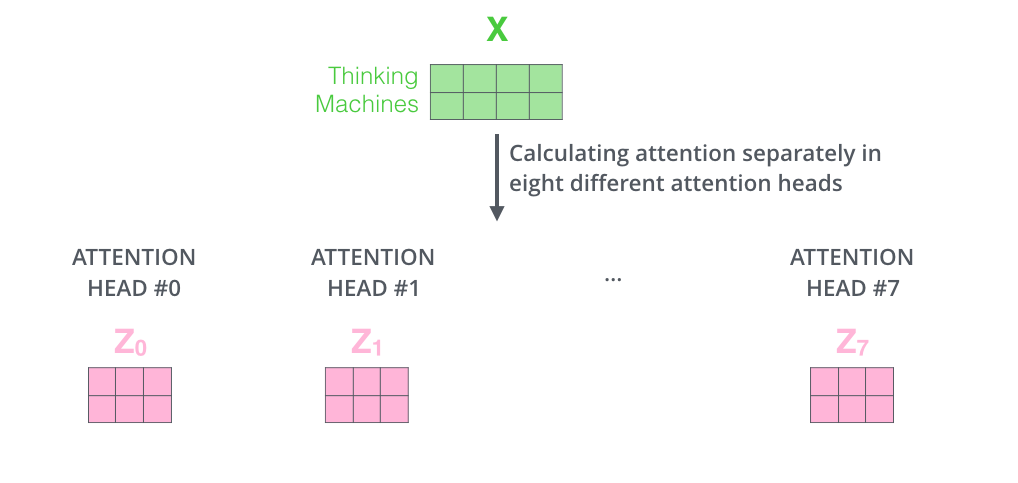
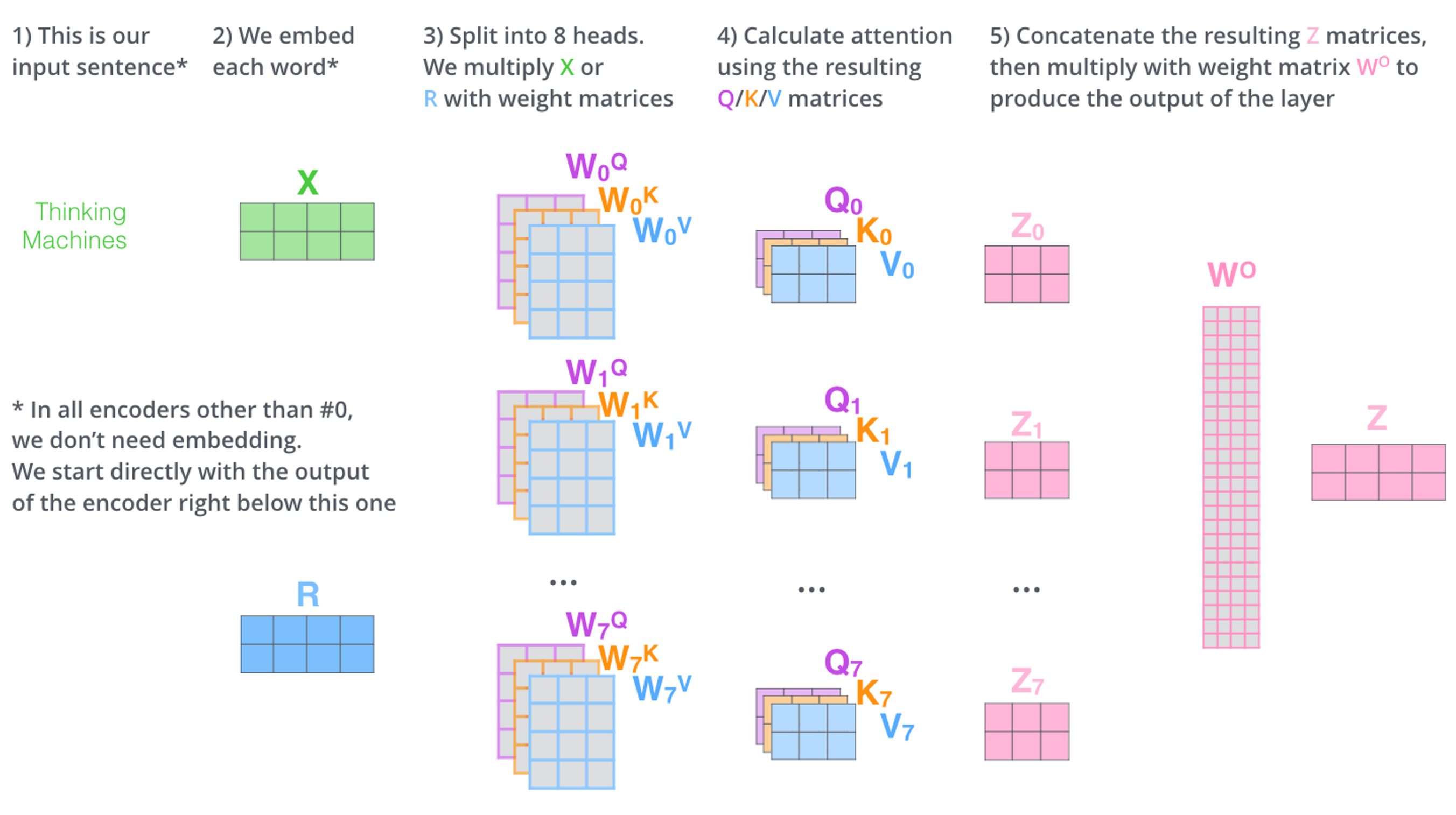
1. 입력 벡터들의 모음인 행렬 X를 ( 로 곱해 각 head에 대한 Q/K/V 행렬들을 생성한다.
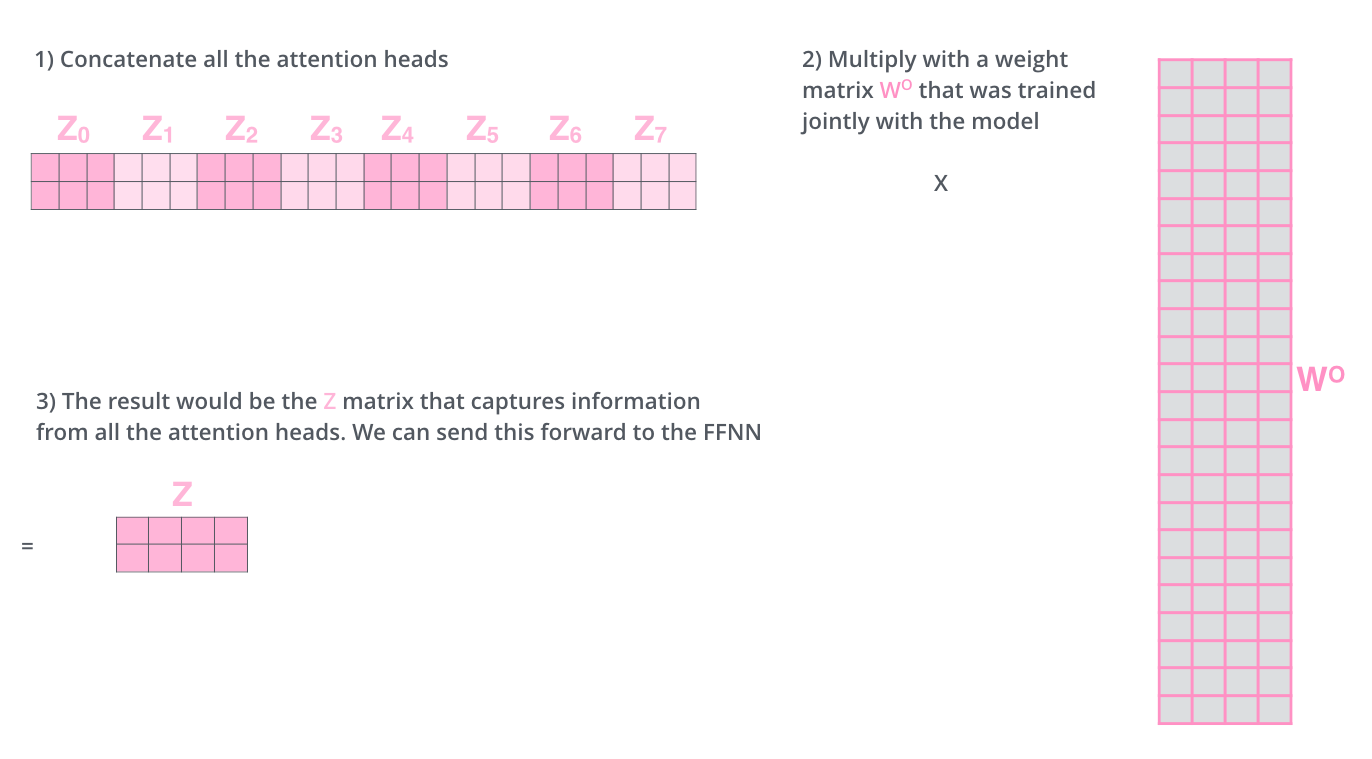
- self-attention 계산 과정을 8개의 다른 weight 행렬들에 대해 8번 거치게 되면, 우리는 8개의 서로 다른 Z 행렬을 가지게 된다. 그런데 이 8개의 행렬을 바로 feed-forward layer으로 보낼 수 없기 때문에,
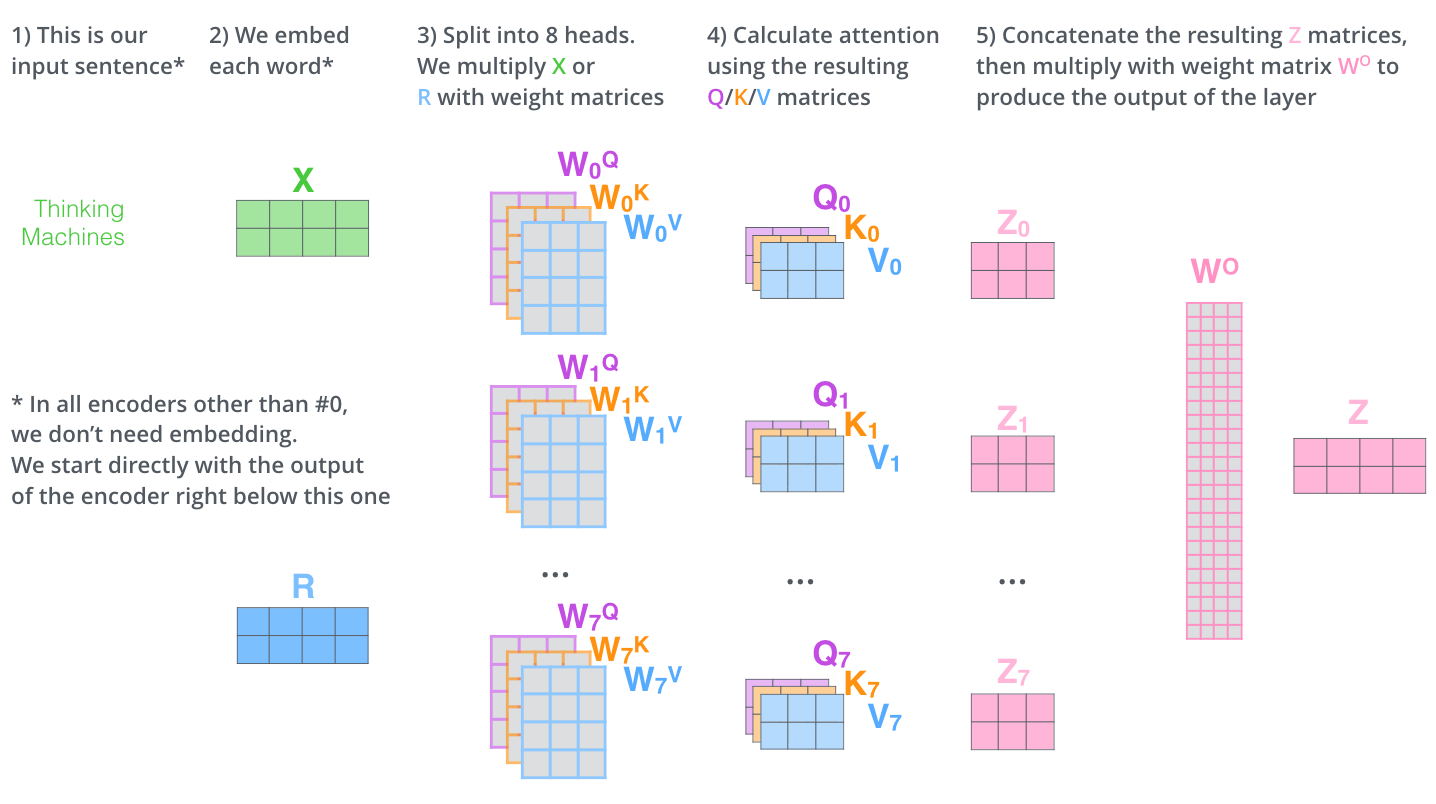
concat을 해서 하나의 행렬로 만들어버리고, 하나의 또 다른 weight 행렬인 W0을 곱해버린다.
이를 정리하면 다음과 같다.
Reference
위키피디아
jhtobigs.oopy.io
blossominkyung 블로그
pozalabs 블로그
트랜스포머 (어텐션 이즈 올 유 니드)
