[Transformer A to Z] 2. Input embedding, Positional encoding

InAnarchy·2024년 5월 16일

Transformer

목록 보기

2/5

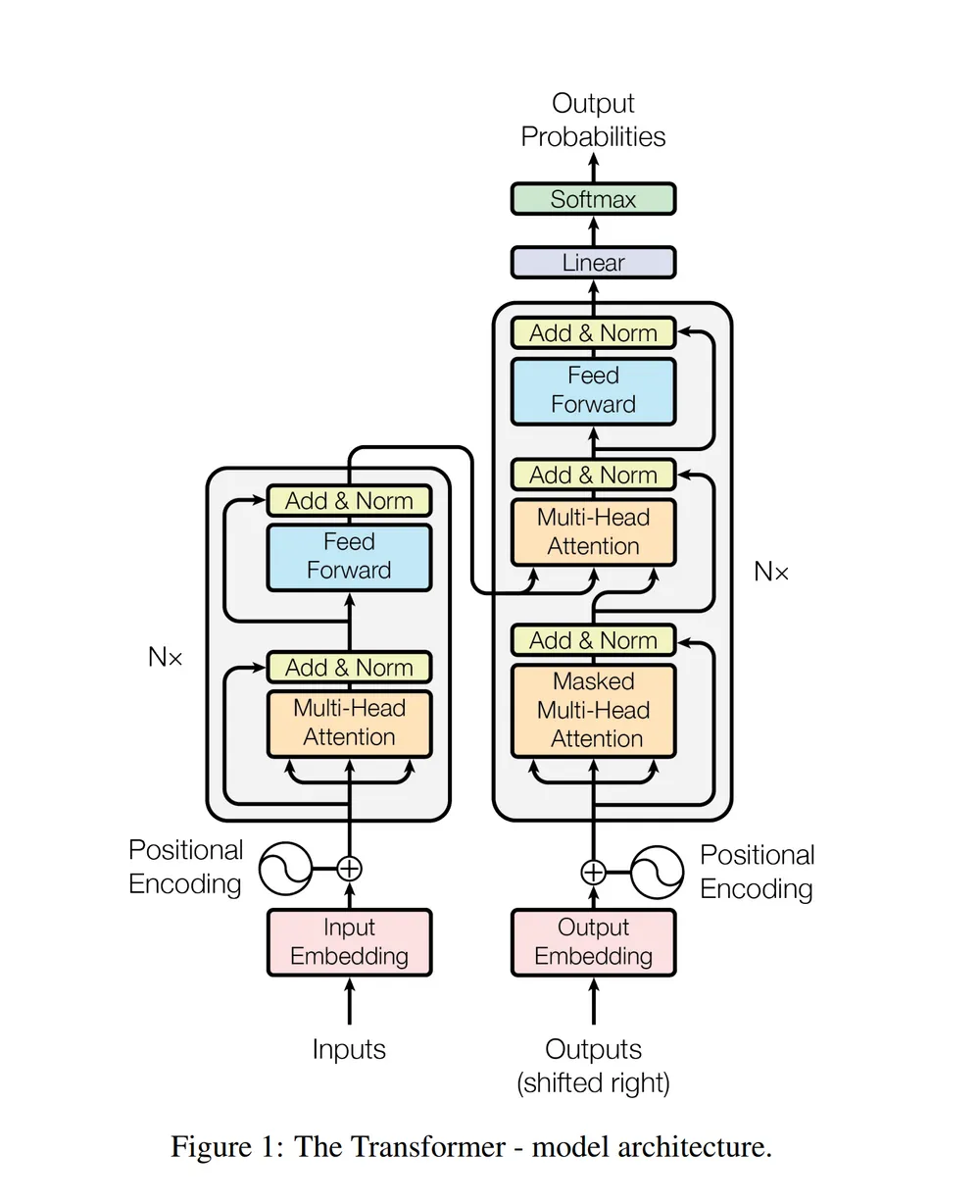
위 사진(트랜스포머 아키텍처)에서, encoder에 들어가기 전
Input Embedding과 positional encoding이 이루어지는데,
본 게시글에서는 이 두가지에 대해 알아보려 한다.

이 때 문장들이 인코더에 들어가기 위해서 어떻게 해야할까? 바로 임베딩 알고리즘을 이용해 벡터로 변환해야한다.
본 논문에서 각 단어들은 크기가 512인 벡터 하나로 임베딩된다.(self-attention layer에 들어가기 전에)
참고로 인코더를 6번 쌓았다고 했는데, 이 임베딩은 가장 밑 단의 인코더에서만 일어난다.
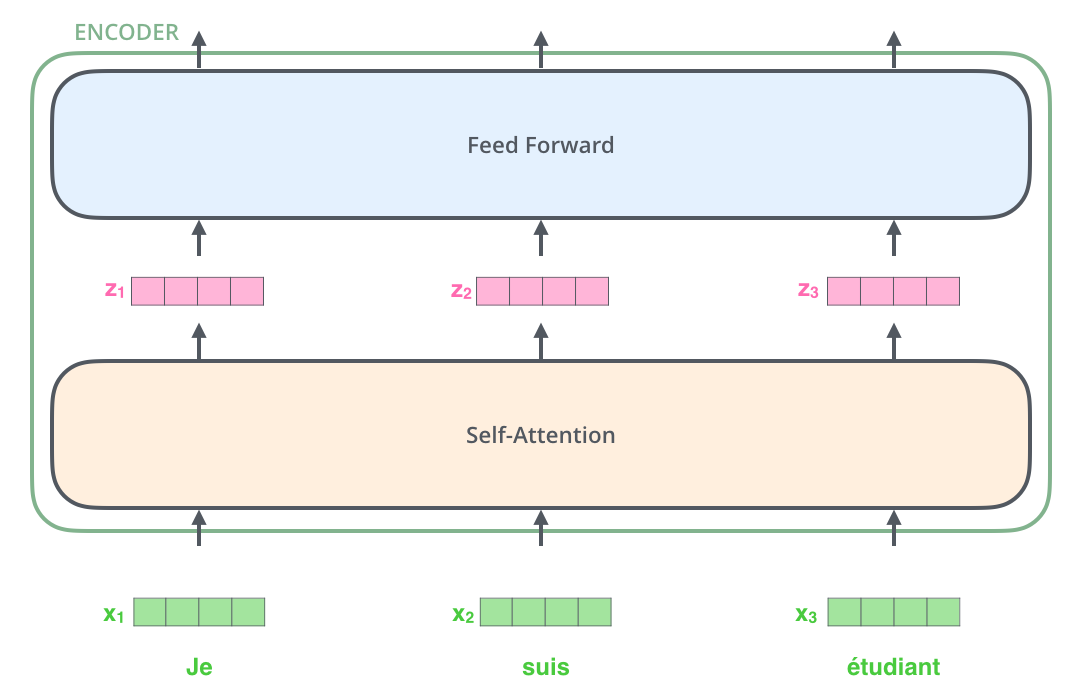
입력 문장의 단어들을 embedding 한 후에, 각 단어에 해당하는 벡터들은 encoder 내의 두 개의 sub-layer으로 들어간다.(위의 사진에서는 3개의 토큰으로 했다.)

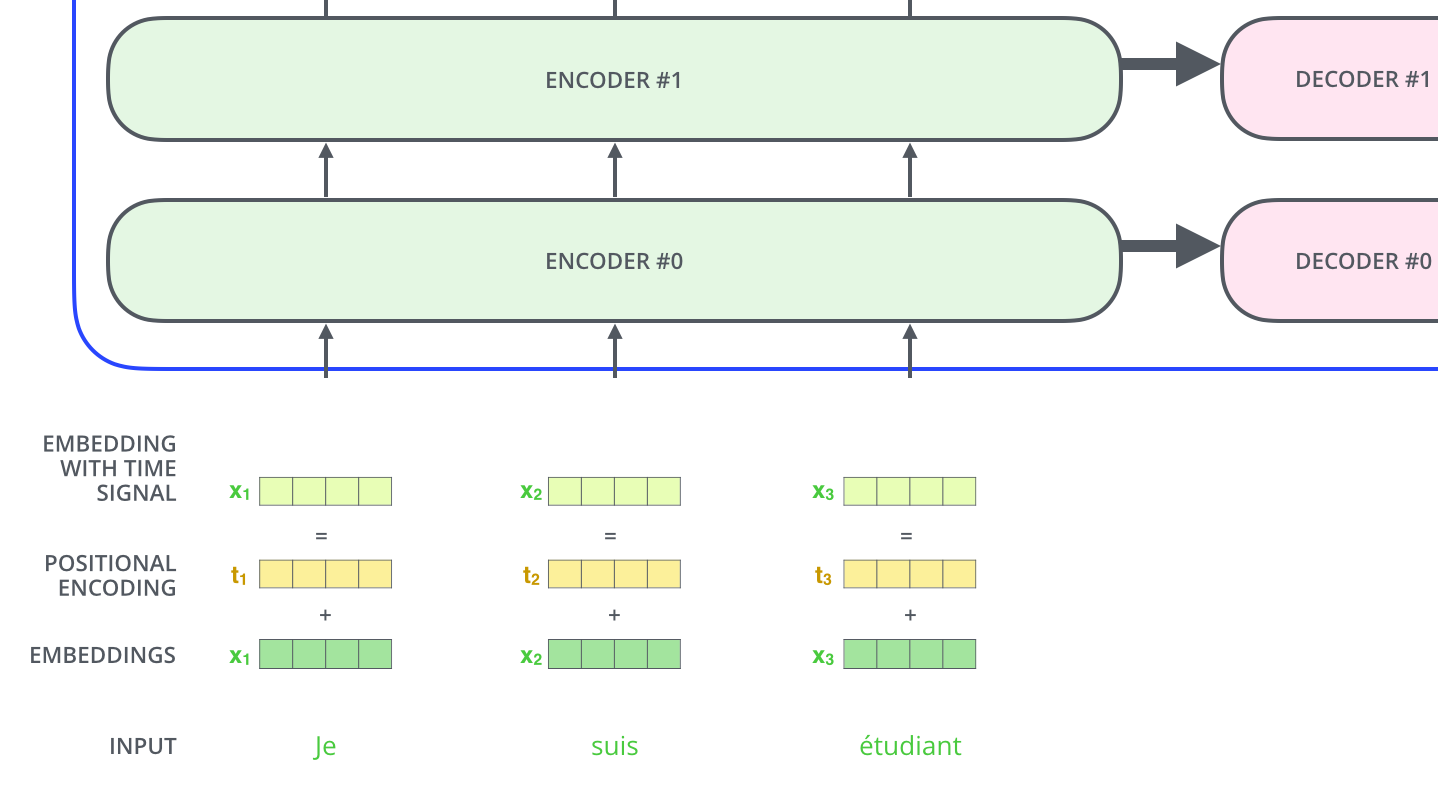
input 문장은 Je suis etudiant이고, 이를 input embedding하여 x1,x2,x3과 같이 나타내었다.
단어의 순서에 대한 정보를 주기 위하여, 위치 별로 특정한 패턴을 따르는 positional encoding 벡터 t1,t2,t3 들을 추가해서 더한다.
이 때 더한다는 것은 말 그대로 add(1 add 2 ->3)로, concat(1 concat 2 -> 12)과는 다르다.
본 논문에서 크기가 512인 벡터로 input embedding한다고 위에서 서술한 바가 있는데, 그렇다면 positional encoding 벡터 역시 크기가 512일 것이다.

Q. 그렇다면 Positional Encoding이 만족해야 하는 조건들은 무엇일까?

각 위치값은 시퀀스의 길이나 입력값에 관계없이 동일한 위치값을 가져야 한다. 즉, 시퀀스 데이터가 변경되더라도 위치 임베딩은 동일하게 유지되어 입력값에 대한 순서 정보를 유지할 수 있어야 한다.
모든 위치값이 입력값에 비해 너무 크면 안 된다. 위치값이 너무 커져버리면 데이터가 가지는 의미값이 상대적으로 작아지게 되므로 입력값이 왜곡된다.
Positional Encoding의 값이 빠르게 증가되면 안 된다. Positional Encoding의 값이 너무 빨리 커지게 되면 증가된 위치에 weight가 커지게 되고 gradient vanishing/exploding 등의 문제가 발생할 수 있다.
위치 차이에 의한 Positional Encoding 값의 차이를 거리로 이용할 수 있어야 한다. 따라서 등간격으로 배열된 부드러운 곡선 형태를 사용한다.
Positional Encoding 값은 위치에 따라 서로 다른 값을 가져야 한다.

Positional Encoding 방법에 대해 생각해보면
1. [0,1] 사이의 각 time-step(0은 첫번째 단어, 1은 마지막) 에 숫자를 할당하는 방법

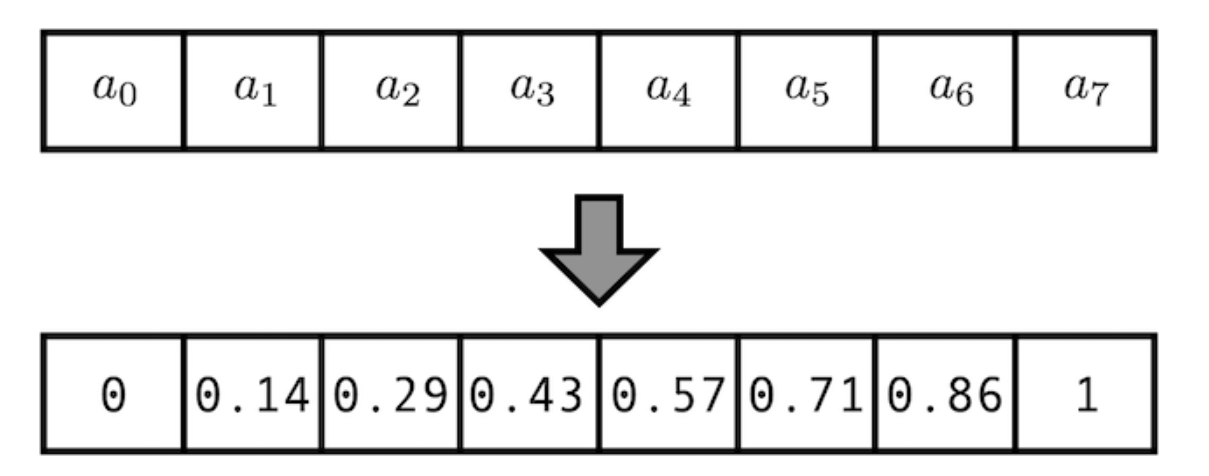
이 경우 길이가 다른 데이터끼리는 각 단어가 일관된 의미를 갖지 못한다.

즉 1. 각 위치값은 시퀀스의 길이나 입력값에 관계없이 동일한 위치값을 가져야 한다. 조건을 위반한다.

각 time-step에 선형적으로 숫자를 할당하는 방법
첫번째 단어는 1, 두번째 단어는 2,.. 이런 식으로.

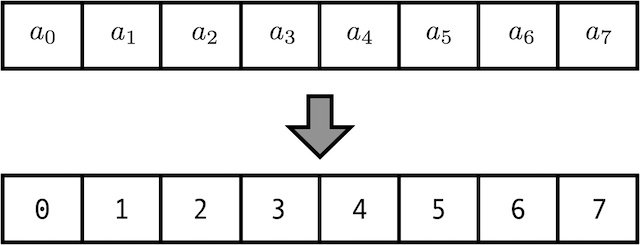
이 경우 값이 커질 수록 모델 훈련 시 학습할 때보다 큰 값이 입력값으로 들어오게 될 때 문제 발생 모델의 일반화가 어렵게 된다.
즉
모든 위치값이 입력값에 비해 너무 크면 안 된다
Positional Encoding의 값이 빠르게 증가되면 안 된다
의 조건을 위반한다.
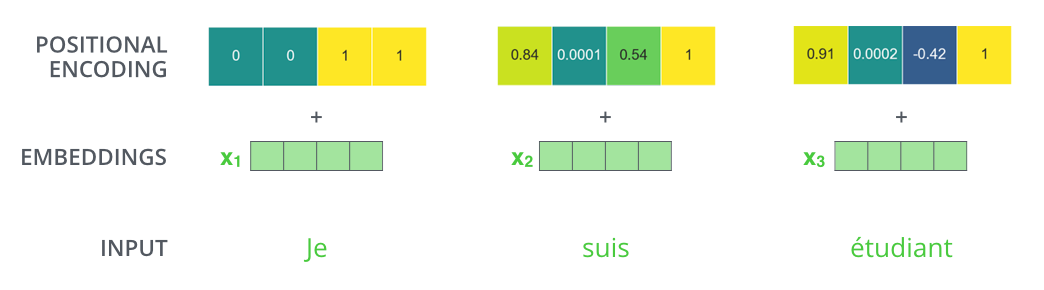
positional encoding vector가 스칼라값이 아닌 d-dimensional vector를 사용하는 방법

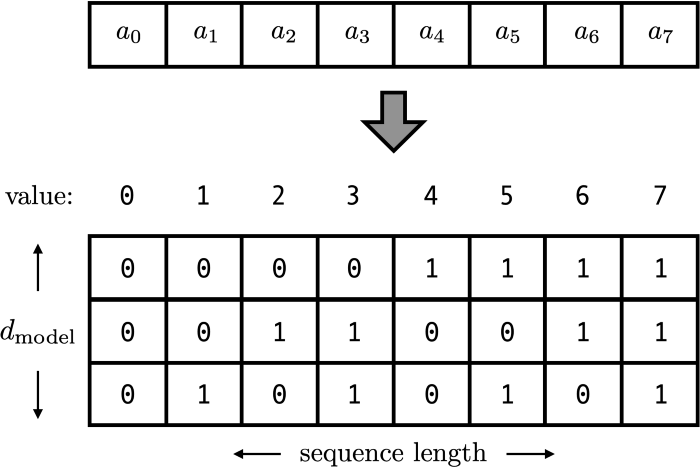
이 경우에는 값도 0과 1사이이고, 가변적인 길이에도 같은 위치에는 같은 값이 할당된다.

그런데 문제가 있다. 다음 사진의 그래프를 보자.

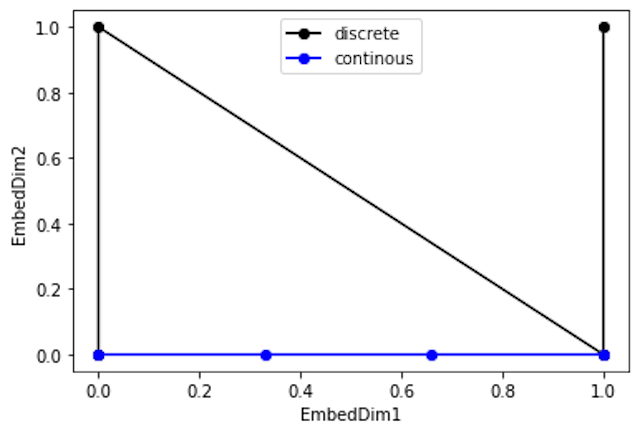
파란 선의 점 사이 간격은 동일한데,
검은 선의 점 사이 간격은 동일하지 않다.
즉 검은 선과 같은 positional encoding 값은 4. 위치 차이에 의한 positional encoding 값의 차이를 거리로 이용해야한다는 조건에 부합하지 않는다

그렇다면, 저 5가지 조건을 모두 만족하는 함수는 뭐가 있을까? 바로 삼각함수이다.

삼각함수는 -1에서 1사이 값을 주기적으로 부드럽게 움직이기 때문에, 위의 조건들을 만족한다.
그래서 트랜스포머에서는 다른 frequency를 가지는 sin, cos를 사용한 positional encoding을 사용한다.
그런데 데이터의 길이가 길어지게 되면 반복이 발생하여 Positional Encoding 값은 위치에 따라 서로 다른 값을 가져야 한다는 조건을 만족할 수 없게 되어,
$Asin(Nx)$ 에서 위치에 대한 고유값을 가지게 하기 위해, 주기를 길게(진동수를 작게) 만들기 위해서 N의 크기를 줄인다.
그래서 본 논문에서는 N의 값을 1/10000과 같이 아주 작은 수로 사용했다.
마지막 5. 위치 차이에 의한 Positional Encoding 값의 차이를 거리로 이용할 수 있어야 한다는 조건을 만족하기 위해서는 position의 변경량을 선형변환으로 나타낼 수 있어야 한다.
그런데 cos과 sin을 번갈아 사용하여, 각 index 별 positonal encoding vector 간의 선형변환이 가능해진다.

(조금 더 추가 예정)

github blog 쓰다가 관리하기 귀찮아서 돌아왔다