Step 1: Shingling -> Step 2: Min-hashing -> Step 3: Locality Sensitive Hashing

Locality Sensitive Hashing

목표: 자카드 유사도가 충분히 높은 문서들을 찾는 것
아이디어: 시그니쳐들을 해싱함수를 통해서 버킷으로 보낸다 -> 이것을 통해서 후보해를 찾는다.

시그니쳐를 일부분만 잘라서 해싱함수에 적용한다. 이때 정확히 같은 버킷으로 들어간 시그니쳐를 후보쌍으로 지정한다.(일부분에 대해서 시그니쳐가 같기 때문에 유사도가 있다고 할 수 있음)

문턱값(S)에 대해서 시그니쳐가 S만큼 유사하면 그때 후보쌍으로 지정한다.

주요 아이디어: 시그니쳐를 잘라서 여러차례 해시함수에 넣어준다.
그 중 같은 것들을 후보쌍으로 지정한다.

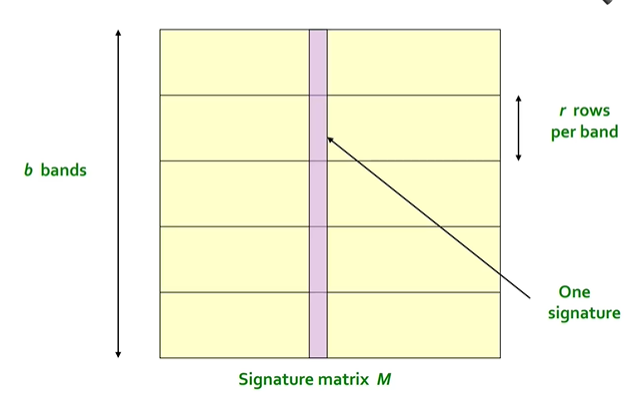
시그니쳐 행렬 M에서 하나의 열을 살펴보자
하나의 열은 b개의 밴드로 나눠지고, 하나의 밴드안에 r개의 행(원소데이터)들이 존재한다.

이때 버킷의 개수는 충분히 크게 해줄 수록 좋다.
적어도 1개 이상의 밴드에서 같은 버킷에 들어가면 후보해라고 하자.

두 문서의 유사도가 0.8일때 두 문서의 밴드가 같은 버킷에 들어갈 확률은 얼마일까?
(0.8)^5 = 0.328
만약 20번 할때 전부 같은 버킷에 담기지 않을 확률은 0.00035이다 ->false negative
즉, 대부분 다 같은 버킷으로 들어온다.

두 문서의 유사도가 0.3일때 하나의 밴드에서 정확히 일치할 확률은 (0.3)^5 = 0.00243이다
20개의 밴드가 전부 같은 버킷에 담기지 않을 확률은 0.0474이다
이때도 유사할 가능성이 높다 -> false positive

이렇게 때문에 false negative와 false positive의 밸런스를 맞춰야 한다. r을 통해서
우리가 원하는 것은 임계치를 넘으면 백프로의 확률로 같은 버킷에 담기고,
넘지못하면 100프로의 확률로 다른 버킷에 담기게 하는 것이다.
실제로는 이렇지 못하다

b개의 밴드, r개의 행이 있다고 했을 때
C1과 C2가 후보쌍이 될 확률 ?
두개의 유사도를 t라고 가정하자.

하나의 밴드에서 모든행이 일치할 확률 $t^r$
어떤 밴드에서 일치하지 않을 확률 $1-t^r$
모든 밴드가 일치하지 않을 확률 $(1-t^r)^b$
모든 밴드에서 하나라도 일치할 확률 $1-(1-t^r)^b$

이 공식을 통해서 우리가 원하는 그래프를 유도해야 한다.

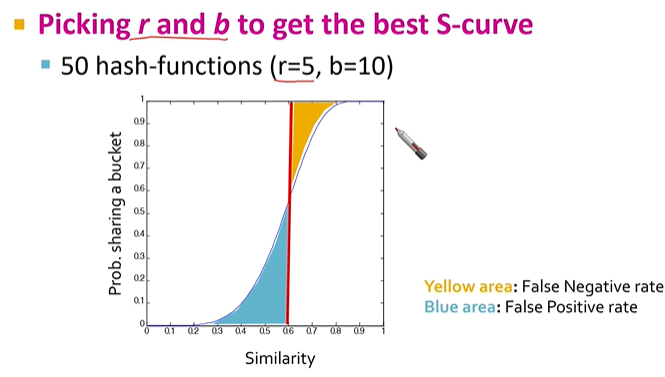
실제에서는 메모리 문제로 후보쌍이 일치하지 않아도 같은 곳에 담길 수 있기 때문에 확인하는 작업이 필요하다.